一道习题引发的思考——小学数学中“等积变换”问题摭谈

彭龙龙

（厦门市华昌小学，福建 厦门 361000）

一、缘起课堂，诱发思考

炎炎夏日，又到了一年的小学毕业复习季，笔者正在复习“求阴影部分的面积”一课，此时的学生听意正浓，当笔者出示一道题：“如右图一个直角梯形，求阴影部分的面积。”几乎全班的学生直接利用各部分面积与总面积的关系来解题即S阴=S梯－S空白=（8+5）×4÷2－5×4÷2=16。可恰恰在此时，一位学生的解法却打破了这份平静，令人眼前一亮。他首先做了一条辅助线AC，则根据同底等高△ADE的面积等于△ACE的面积，那么两个阴影部分的面积之和瞬间就转化成了一个直角三角形ABC的面积，所以

S阴=S△ABC=8×4÷2=16。这种解法实在太妙了，仅仅只是添加了一条辅助线，人为地创造出一个“等积”的环境，将零散的阴影面积转化成一个整体，等积变换功不可没。可是等积变换如此神奇、重要，学生能应用的却是凤毛麟角，我们深知的“授人以鱼，不如授人以渔”此时此刻黯然失色，笔者不禁陷入深深的思索当中……

二、追本溯源，融汇贯通

回顾小学阶段所接触过的关于“等积变换”类型题目，从低年级所遇到过的数与代数领域中的求括号里的数，如4×5=（）×2，以及解决问题中“二年（1）班排队列，如果每队排10人，可以排4列，如果每队排8人，可以排多少列？”的这种数字世界里的类似归总问题的“等积变换”问题的雏形，以及中高年级所学到的单位改写、乘法结合律和交换律方法、通分、等式的性质解方程等，直到面积、体积概念的深入，等积变换问题才逐步向二维、三维的图形与集合领域过渡，慢慢成型，形成具有自身特色的一类题型。平行四边形面积的推导，就是利用了等积变换的思路，一个未知的图形在不改变面积大小的情况下，通过剪、拼、移转化成了长方形，进而发现等积背后的各部分之间的对应关系，最后顺利推导出面积公式；再把目光聚焦于小学阶段中一个非常重要的立体图形圆柱体，它的体积推导颇具特色，因为要将学生置于一种圆柱体被无穷尽等分，其实是极限思想的数学环境前提下，去理解和掌握圆柱体等分后拼组而成的一个近似的长方体，然后利用等积变换，进而推导出圆柱体的体积公式。最后不得不提的是，小学阶段中测量不规则物体体积的方法，即排水法的应用，也是等积变换的典型例证。由此发现等积变换在小学阶段一直贯彻始终，“等积”是解题的好帮手，为解题亮起一盏明灯，它的重要性自然不言而喻。

三、策略应对，有效实施

既然等积变换如此重要，又千变万化，面对这样的变化，该如何应对，如何在解题中发现“等积”的踪迹呢？笔者经过实践研究，逐渐摸索出以下六大解题策略。

策略一：化零为整

例题：已知正方形的边长为5厘米，求阴影部分的面积。

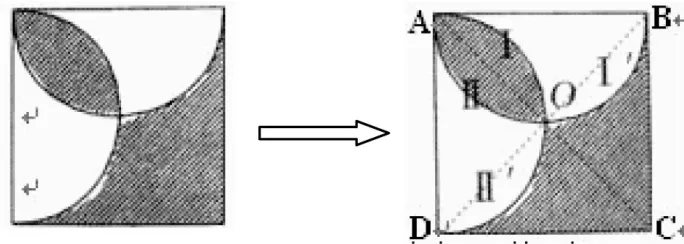
解析：阴影部分的图形是不规则的、是零散的，但只要连接正方形对角线AC、BD，根据正方形的对称性与圆的对称性可知，阴影Ⅰ可拼在I’处，阴影Ⅱ可拼在空白Ⅱ’处，通过化零为整，把阴影部分转化为一个三角形，求阴影的面积就等价于求三角形△BCD的面积。5×5÷2=12.5（平方厘米）。由此想到数学世界里的图形面积往往都是零散的、不规则的，这就需要运用割补、剪拼化零为整，变无形为有形，那么“等积”自然就水到渠成了。

策略二：静中求动

例题：求下图阴影部分的面积。（单位：厘米）

解析：将原图的上半部分沿着圆的直径旋转对折，正好与下半部分的半圆重合，得到右上图，这时的阴影部分的面积就转化为两个底是20÷2=10（厘米）、高是5厘米的三角形面积之和。S阴=10×5÷2×2=50（平方厘米）。该策略与上一策略有异曲同工之妙，唯一区别是化静态图为动态图，让等积思路在操作中自然生成，慢慢发酵。

策略三：以形补形

例题：一件零件的形状如下图，求该零件的体积是多少立方厘米？

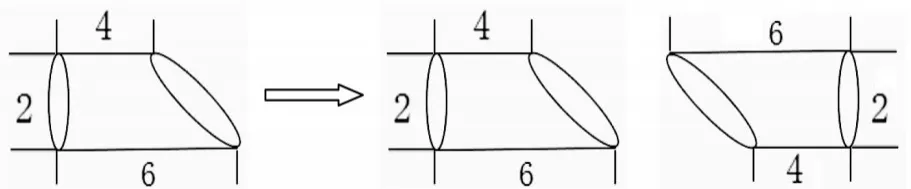
解析：初次见到此题，学生们都认为无解，因为学生并未见过这样的不规则立体图形，似圆柱非圆柱，似圆锥非圆锥。可是只要能转变思考角度，利用原来图形以形补形，如右图，“等积”踪迹已然找到，该零件的体积即一个底面直径为2厘米，高为4+6=10（厘米）的圆柱体积的一半，问题也就迎刃而解。V零件=π×（2÷2）2×10÷2=15.7（cm3）。

策略四：突破关键

例题：把一个长、宽、高分别为9厘米、7厘米、3厘米的长方体铁块和一个棱长是5厘米的正方体铁块熔铸成一个圆柱体，这个圆柱体的底面直径是20厘米，高是多少厘米?

解析：本题的关键是正确理解题目中的关键字“熔铸”，类似这样的词语还有“锻造”“浇铸”“捏成”“铺满”“倒入”等，突破这些关键字词背后的涵义即等体积，这类题型就能从容以对。此题中V柱体=V长方体+V正方体，即形状变，体积不变，再用体积除以底面积，就能得到高。h=（9×7×3+53）÷（π×102）=1(厘米)。

策略五：借形换形

例题：一个长为10分米，宽为6分米的长方形纸片，要将它剪成半径是1.5分米的圆形，问最多可以剪多少个？

解析：常规解法是利用长是直径的几倍即每行剪几个，宽是直径的几倍即可以剪几行，然后再相乘算出一共有多少个圆形，算式是：（10÷3）×（6÷3）≈3×2=6（个）。但即使教师不断强调，学生的错误率仍然较高，甚至不明白为什么要除以直径而不是半径，教师也只能解释因为圆是不能密铺的，所以要这样做，学生自然不明其理。其实只要再往前走一小步，借正方形之形替换圆形，如右上图，告诉学生剪一个半径为1.5分米的圆形其实等价于剪一个边长为3分米的正方形，这样另辟蹊径的“等积变换”，学生也能较容易接受。

策略六：方程求解

例题：下图中圆的面积与长方形的面积相等，长方形的面积是12.56cm2，圆的半径是多少厘米？

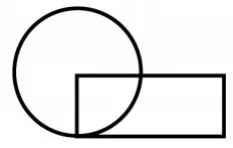
解析：初看此题，学生不难发现等积踪迹，因为题目中已清晰指出：圆的面积等于长方形面积。可是即使如此，学生仍然无从下笔。此题错误的原因是学生缺乏方程意识和代数思维。其实只需将圆的半径设为r，根据S圆=S长方形等积列出一个方程即πr2=12.56，，即可得到πr=12.56，r=2。由此得出列方程解决问题的意识与能力要植入到图形问题中来，让学生形成解题的思维与习惯。

参考文献：

［1］董江青，裴云姣.利用三角形等积变换求组合图形面积教学［J］.小学教学设计，2013(9).

［2］陈涛清.小学数学几何直观教学的优化策略［J］.教学与管理，2015(2).