变积分限两个卷积核与奇异核混合的积分方程的求解

晏　丽

1977年，前苏联学者Duduchava，R V［1］首次研究具有卷积核的积分方程.1987年，路见可教授［2］又进一步提出了将带有常系数的卷积核与Cauchy核混合的奇异积分方程通过由Fourier变换将其转化为Riemann边值问题来求解的方法，同时在{0}类中研究了正则型情况下的一般解法.沈永祥教授［3］以及孙凤琪教授［4］等人在路见可教授研究的基础上，更深入地研究了有关卷积核与奇异核混合的积分方程的求解问题.冯志新教授［5］近期又研究了卷积核与奇异核混合的变积分限的对偶型完全奇异积分方程的求解问题.

本文在上述研究结果的基础上，在{}0函数类中讨论了一类变积分限且两个卷积核与奇异核混合的奇异积分方程的求解问题.我们利用积分变换将讨论的积分方程转化为等价的具有间断系数的Riemann边值问题，再利用Fredholm方程理论，讨论该类方程的可解和需添加的相应可解条件，从而得到其在{}0类中一般解.

1　变积分限两个卷积核与奇异核混合的积分方程的转化

设讨论的积分方程为

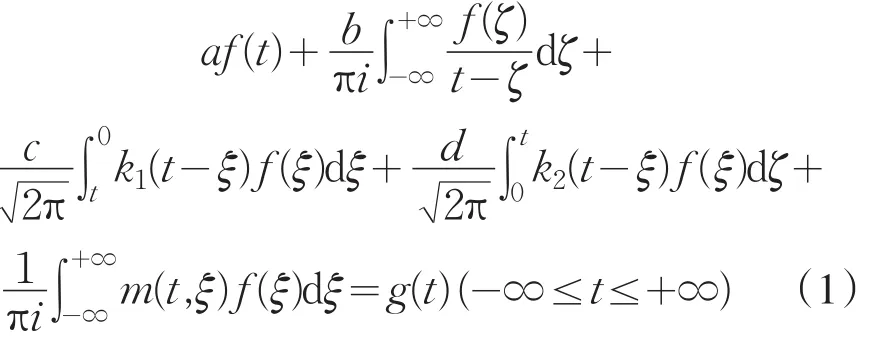
令

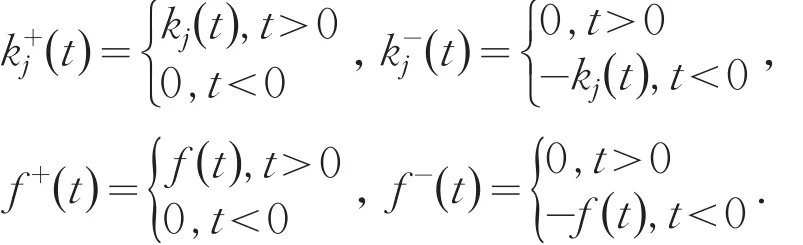
t-s.

利用以上记号，可将变积分限的两个卷积核与奇异核混合的积分方程（1）化为

进一步将上式扩充到(-∞,+∞)，则（1）式可改写为

由符号函数sgnt及 f±(t)的定义，则.将（2）式再改写为

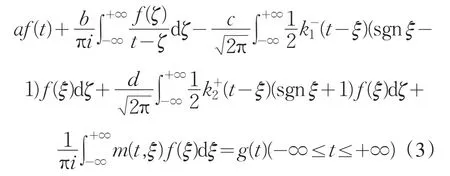
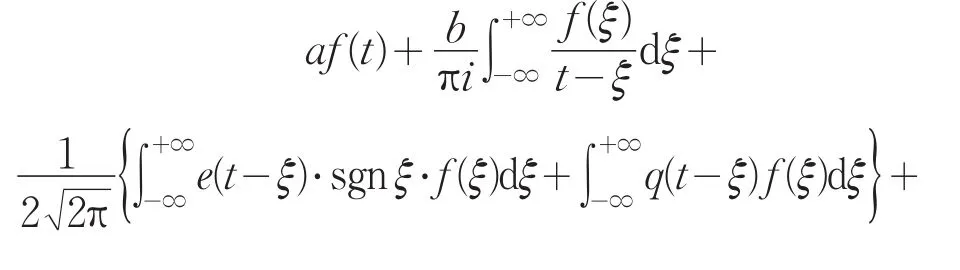
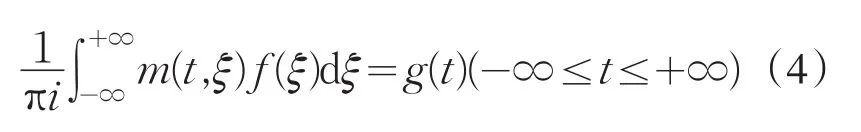
根据Fourier变换性质，用Fourier算子V 作用（4）左右两端，整理后得

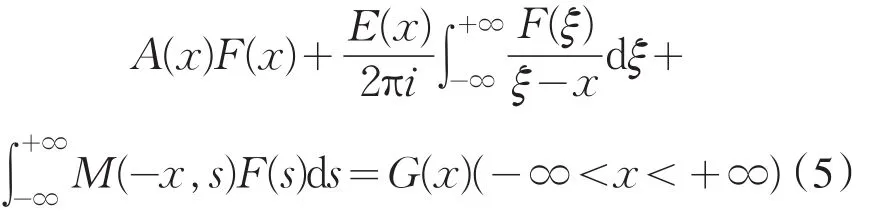
（1），可 化 为 在 {{0}}类中 求 解（5）.注 意

2　变积分限两个卷积核与奇异核混合的积分方程的求解

不失一般性，本文主要讨论正则型问题，故假设

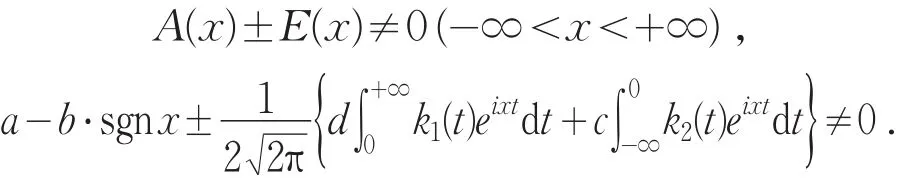
对于奇异积分方程（5）的特征方程

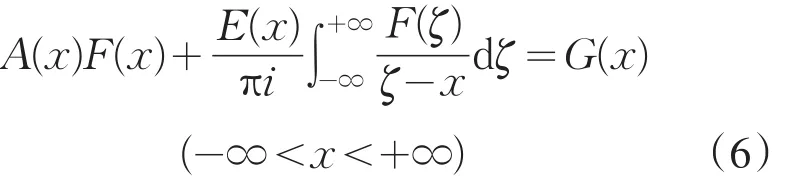
x=0显然也是积分方程（6）的结点.为讨论方便，暂视其为光滑点，所需添加的可解条件将进一步专门予以讨论.

对于特征方程（6），由于在{{0}}类中求解，按文 献 ［6］ 的 方 法 ，记γ∞=α∞+iβ∞=，故完全积分方程（5）的指标k=α∞，当k≥0时，则特征积分方程（6）在R-1类中的一般解为

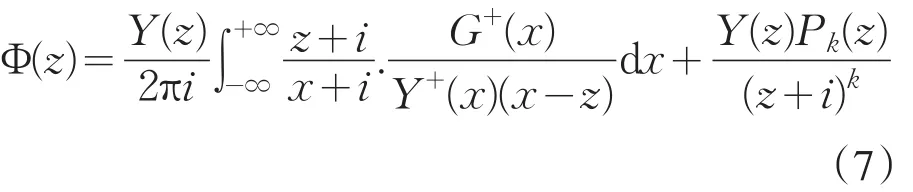
其中，Pk(z)为k阶的任意多项式.

当k≤0时，Pk(z)≡0.

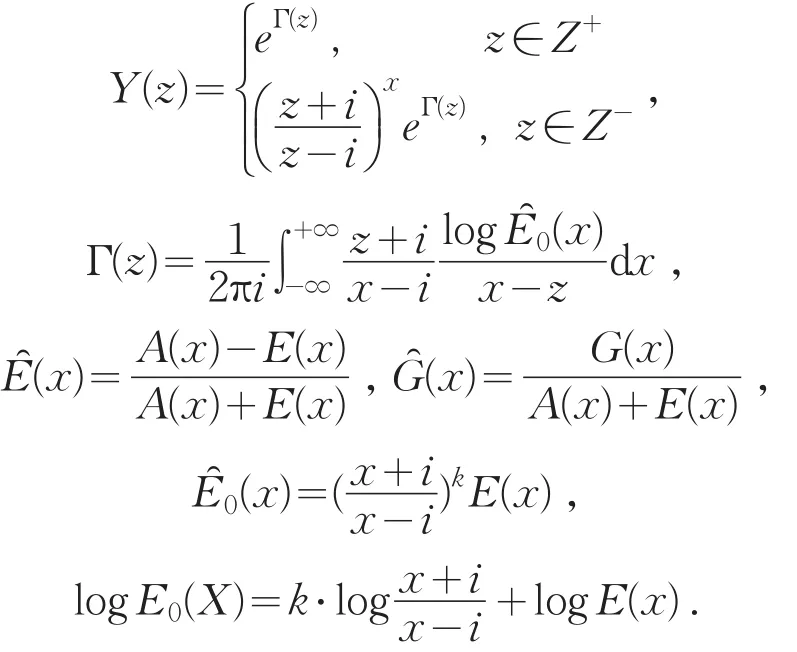
易见z=-i是Φ(z)的奇异点.为使Φ(z)在z=-i处解析，还需假设

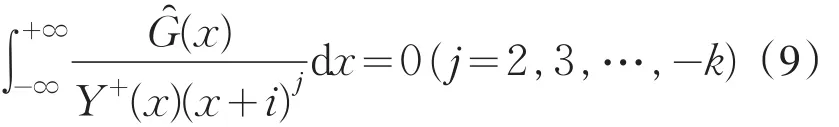
当 k≤0时，Pk(z)≡0特征积分方程（6）在R-1类中的一般解为

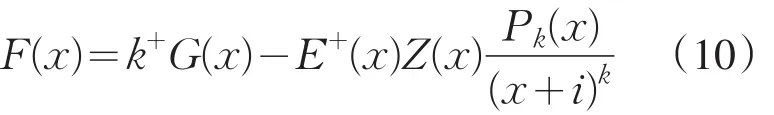
再将（5）式改写成

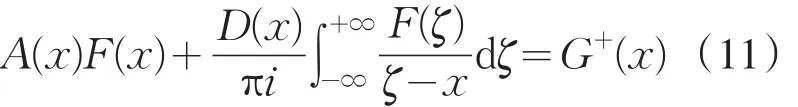
所以，完全奇异积分方程（5）已转化为{{0}}类中在同解意义下的Fredholm积分方程（12）.k≤0时，仅当（9）式成立并且 F(t)满足

在{{0}}中可解.因而，在暂且不考虑在结点x=0处的性态的条件下，求解（6）等价于在{{0}}类中求解方程（12）或（14）.

受到外界和他人的影响，农村留守儿童容易产生行为偏差，沉溺于游戏厅和网吧等娱乐场所，法律意识淡薄，出现违法违纪现象。农村留守儿童问题具有长期性和特殊性的特点，关心不同性别、不同年龄段留守儿童的需求，有利于促进留守儿童的身心健康发展。

若k≥0，由Fredholm积分广义预解核理论（12）可解的充要的条件

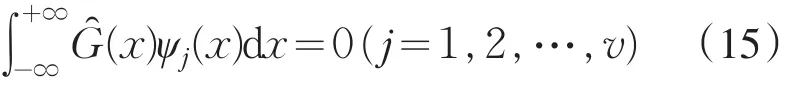
成立时，Fredholm积分方程可解.

奇异积分方程（5）在{0}类中的一般解为

其中，γ(x,τ)为方程的广义预解核.

若k≤0，（14）可解充要的条件

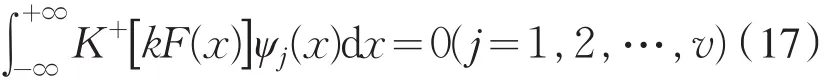
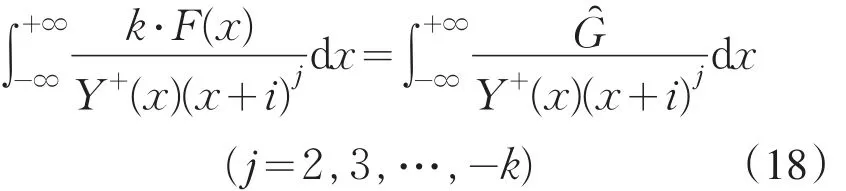
3　在结点x=0处添加的可解条件讨论

先设 x=0为普通端点.不失一般性，设x=0为起始弧端点.记 γ=α+iβ，0≤α≤1，由端点附近Cauchy型性质对以(f(s)∈{0},γ=α+iβ（0≤α≤1））为密度函数的Cauchy型积分，由文献［5］知，在x=0附近有.其中在x=0附近解析且属于{{0}}函数类（c=0+(0-)）.由Φ+（z)的表达式（7），在结点x=0附近得到

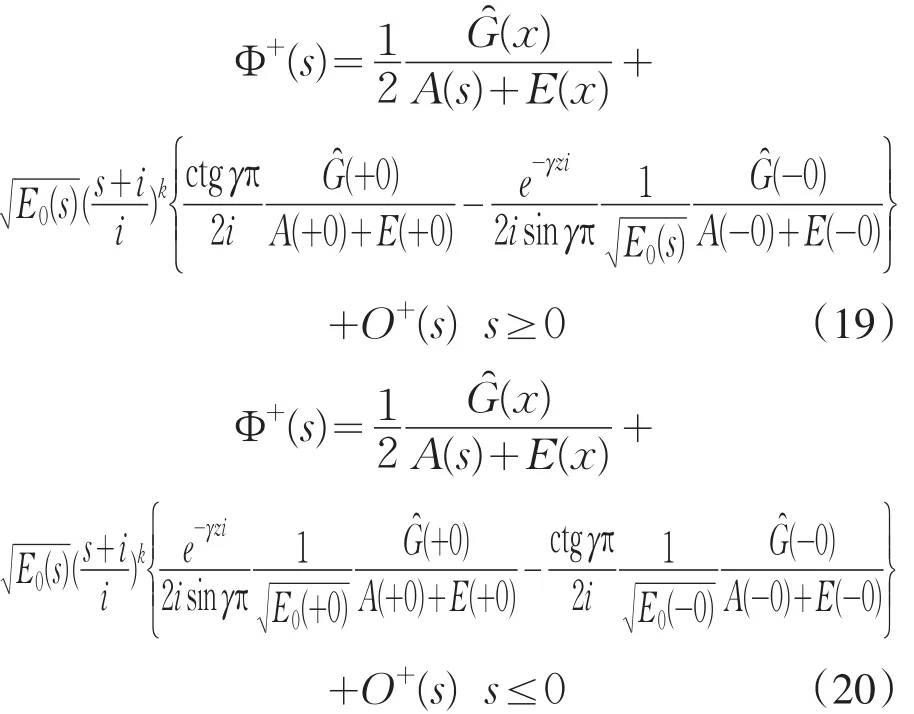
函数 O*(s)在 x=0处解析，且∈{{0}}，当时，

由上式，经计算当s→0+时（当s→0-时同理），有下式成立

由（19）及（20）式，以及Φ+（0）=Φ-(0)，则有，所以此式是积分方程（1）可解的必要条件.再设 x=0是积分方程（1）的特异结点.在端点 x=0附近，设 γ=α+iβ,α=0 ，则 γ=iβ .此时上述讨论均成立，而

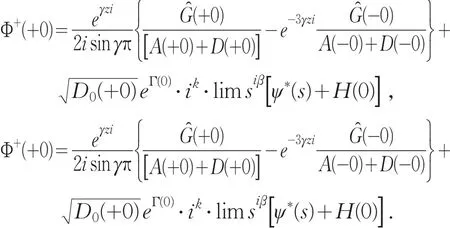
易见，当s→0+或s→0-为保证Φ+（0）=Φ-(0)，须有，因为，无论x=0是问题普通结点或特异结点，可解的必要条件是

参考文献：

［1］Duduchava R V.Integral operators of convolution type with discontinuous coefficients［J］.Math.Nachr.，1977，79（10）：75-98.

［2］Lu Jianke.On methods of solution of singular inte⁃gral equations with convolution［J］.Chin.Ann.of Math.，1987（8）：97-108.

［3］Shen Yongxiang.Some kinds of singular integral equations of Hilbert kernel with convolution［J］.Acta.Math.Sci.，1989，9（4）：421-426.

［4］孙凤琪.含卷积核的完全奇异积分-微分方程的求解［J］.吉林大学学报，2010，48（4）：605-608.

［5］冯志新.变积分线Cauchy核卷积核混合的完全奇异积分方程的求解［J］.吉林大学学报，2013，6（51）：1051-1057.

［6］路见可.解析函数边值问题［M］.武汉：武汉大学出版社，2004.