密封式继电器触点表面与接触还原研究*
李文华 周露露
河北工业大学, 天津300130
继电器触点的表面形貌对继电器长期连续工作状态有直接影响[1],粗糙表面的几何结构会影响接触情况,只有充分了解触点表面接触形貌,才能更好地从微观层面研究触点接触过程中的变化。
随着对粗糙表面研究的不断深入,传统的二维评价方法已经不能满足要求,三维表面形貌的表征可以从不同方面描述粗糙表面,对三维表面的形貌特征分析反而显得越来越重要。在表面三维形貌的研究中,绝大多数学者利用Weierstrass-Mandelbrot(W-M)函数模拟粗糙表面。文献[2]使用W-M 函数对粗糙表面轮廓进行拟合,分析了2个接触粗糙面微凸体个数及其被挤压高度、接触面积W-M函数的关系,推导了粗糙面的接触电阻计算公式,研究了两粗糙面间的接触电阻与接触力的关系。
虽然三维粗糙表面分形方法被越来越多地运用到继电器接触表面的研究中,但这些针对的都是单个触点的表面,对触点组的分析几乎没有。继电器触点接触过程中真实表面的变化很难观测,通过仿真模拟接触过程分析得到的参数不具有真实还原性。文献[3]通过扫描电镜建立了真实的继电器触点接触表面模型,通过仿真研究了接触电阻与接触压力之间的关系,但该方法尚未研究接触区域的热电效应。
因此,本文利用三维非接触式形貌仪采集三维坐标,计算表面的三维粗糙度参数值和分形维数。扫描触点表面元素分布,针对特定元素分析触点的失效机理。从微观角度分析触点表面的接触关系,选定相对触点平面,提出差平面还原触点接触面,为从真实形貌角度进一步建立接触电阻模型提供了思路。
1 三维形貌分析
1.1 三维粗糙度
本文选取试验后的一对密封式继电器触点为样本,利用三维非接触式表面形貌仪扫描得到继电器动静触点的三维表面形貌图如图1所示。
选取最小二乘法建立表面形貌模型,通过对多项式函数求偏导,可以得到多项式中相应的未知参数,建立表面形貌的最小二乘中位面,并以此作为三维表面形貌的评定基准面[4]。目前三维形貌参数主要包括4个方面:幅度参数、空间参数、功能参数和综合参数。本文选取5个代表性的幅度参数进行分析:表面十点高度Sz,表面算术平均偏差Sa,表面均方根偏差Sq,轮廓最大谷深Sv以及轮廓最大峰高Sp[5-6]。

图1 样本继电器触点
1.2 分形维数
目前,对微观粗糙表面的表达及接触分析,主要采用了统计分析和分形理论的方法,分形理论具有尺度无关性,与统计方法相比,可以较好地描述粗糙平面[7]。
二维分形的W-M函数定义式为:
(1)
式中:x为工程表面水平方向的扫描坐标;z(x)为工程表面垂直方向的粗糙轮廓;D为二维分形维数;G为表面特征尺度系数;γ是决定自相似性和频谱密度的尺度系数;L表示分形轮廓的采样长度。
Yan等人将满足分形性质的W-M函数推广到三维粗糙面,可以更精确地描述粗糙表面形貌[8]。三维分形的W-M函数定义式为:
(2)
式中:D为三维分形维数;G为特征尺度系数,反映z(x)幅值大小,它决定z(x,y)的具体尺寸;M为曲面褶皱的重叠数;m,n为随机相位,取值范围为[0,2π]。
分形维数的计算方法有很多种,包括盒维法、差分盒维法、变分法等,其中以盒维法最为常用[9]。本文在非接触式扫描仪扫描的基础上,利用MATLAB软件对图像的分形维数进行盒维法计算。首先读取图1中动静触点的真实表面形貌图,选定相同的触点面积,利用Bernsen算法对其进行二值化处理。针对转化后的二值化图像,用边长为L1的网格覆盖整张图片,数出包含孔和与孔相交的所有网格数N(L1);再把边长L1缩小1倍至L2(L2=L1/2),此时再数出盒子数N(L2)。重复上述步骤,使网格不断变小,盒子数不断变多。最后,以lnN(Li)为纵坐标,lnLi为横坐标作图,线性回归处理得到的双对数坐标图中的数据点,得到一条直线,则直线斜率的绝对值就是分形维数D。
1.3 三维形貌分析
根据采集的继电器触点表面选定区域的三维坐标建立基准面模型,计算得到动静触点三维表面粗糙度参数数据如表1所示。

表1 动静触点三维表面粗糙度参数数据表
由表1分析可知,继电器触头表面形貌的三维参数Sa与Sq之间满足以下关系[10]:
Sa=2σ/π≈0.8σ=0.8Sq
(3)
式中,σ是幅度分布的标准偏差,即Sq表面具有大量随机的、杂乱的尖峰,其表面结构与周期性较强的表面有明显区别。
Sq对偏离名义高度较大的采样点比Sa更敏感,而随机性强的表面中具有大量随机和局部的信息和结构,使得Sq值总是偏大。对于随机性较强的表面,Sa/Sq的值都小于0.8;对于规律性较强的表面,Sa/Sq的值基本上略大于0.8。因此,继电器动触点表面结构周期性越弱,静触点表面结构的周期性越强。
分析继电器动、静触头的最大峰高和最大谷深之和,用V表示:
V=Sp+Sv
(4)
由表可知,继电器动触点V值绝对值比静触点的V值绝对值大很多,表明动触点的起伏变化明显,幅度较大,而静触点的幅度变化较小,相对平坦。继电器动静触点表面的粗糙度参数满足以下关系:
(5)
根据三维非接触式形貌扫描仪扫描得到的动静触点的形貌图,按照盒维法计算得到动静触点的二维分形维数和三维分形维数如表2所示。
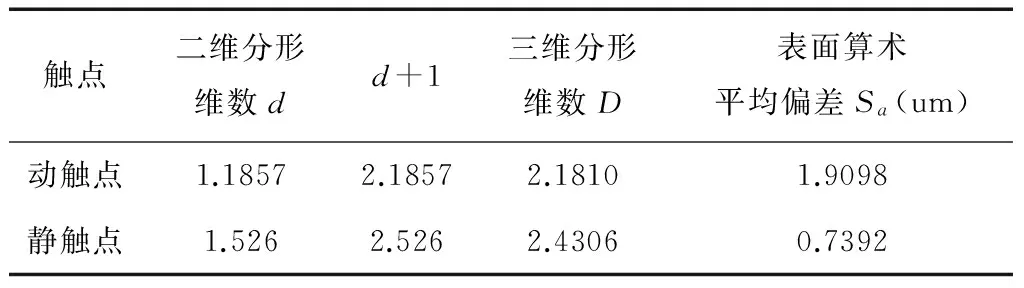
表2 触点组分形维数表
分形维数D与表面微观形貌的幅值变化的剧烈程度有关,D值大表明微观细节丰富;D值越小表明低频成分越多[10]。一般来说,三维分形维数值比二维分形维数值大1;且Sa值小时,D值则较大。这是因为Sa小时,表面的微观结构精细,短波长成分较多,因此D值较大。从三维形貌角度来说,二维或三维粗糙度参数越大,继电器触点的失效越表现为凹凸明显的微动磨损失效形式;反之,触点的失效表现为颗粒沉积形式。
2 表面成分分析
2.1 SEM分析
继电器内部只有塑料导线、线圈骨架、磁铁和塑料底盘等基本元件,触点材料为金。这些物质在加速寿命试验的运动过程中可能会分解出碳氢化合物。触点接触时出现的机械摩擦会形成高分子量的无定型固体粒子,随着运动次数的增多,固体粒子不断堆积,破坏触点表面膜,使触点绝缘。
为了更好地观察动静触点在运动过程中表面形貌的变化,本文利用扫描电镜进行触点表面扫描,图2(a)和(b)分别是继电器动、静触点表面的SEM图。

图2 动静触点表面SEM图
2个触点的表面状态是材料转移的直观表现。直流作用下的材料转移分为细转移和粗转移2种形式,“细转移”在阴极表面形成尖峰,在阳极表面上有狭窄的陷坑。“粗转移”的外形更多是平面状的。试验中动触点与电源正极连接,表现为阳极现象。动触点表面凹凸不平,烧蚀现象比较明显。静触点表面平整,喷溅沉积的微粒大小相对均匀,出现小麻点状,局部有烧蚀出现。触点表面材料从阳极转移到阴极,即从动触点向静触点转移。
为更好地研究继电器的失效机理,分析表3所示动、静触点表面元素含量。

表3 动、静触点表面元素含量
由表3可知,不管是动触点还是静触点,Au,C,N,O的含量很高,S,Ag等元素都较少,其中C,N和部分O均为污染引入。样本所用触点材料为Au,Au是性能相当稳定的金属材料,一般作为镀层材料镀在非贵金属表面。Au镀层较薄时,镀层表面会出现微孔,在长期使用时形成微孔腐蚀,破坏了原来良好的电接触性能,如图2(a)所示。
2.2 特定元素分析
由表3可知,Au和C的含量很高,利用The SIMS Mapper软件分析这2种特定元素的分布。将样品安装在大小为6mm标准SIMS样品架中,确保触点接触的上表面位于分析平面。以MCs +簇的形式收集负二次离子的同时使用5keV Cs +一次离子对触点表面元素进行分析。在保证不影响触点表面损伤的前提下,根据测试深度的不同使成像电流从1nA~50nA变化。选定触点表面分析区域的面积为4mm×4mm,图3显示了动静触点表面Au和C 元素的分布图,右侧图像为2种元素的3D分布图,表面下方的柱体没有参与分析;左侧图像为假设C和Au 2种元素在整个接触表面含量为100%,根据近似的浓度校准含量,纵坐标为原始计数率相对数据;左下方图显示了选定的凹坑深度为800μm处2种元素的相对数据。
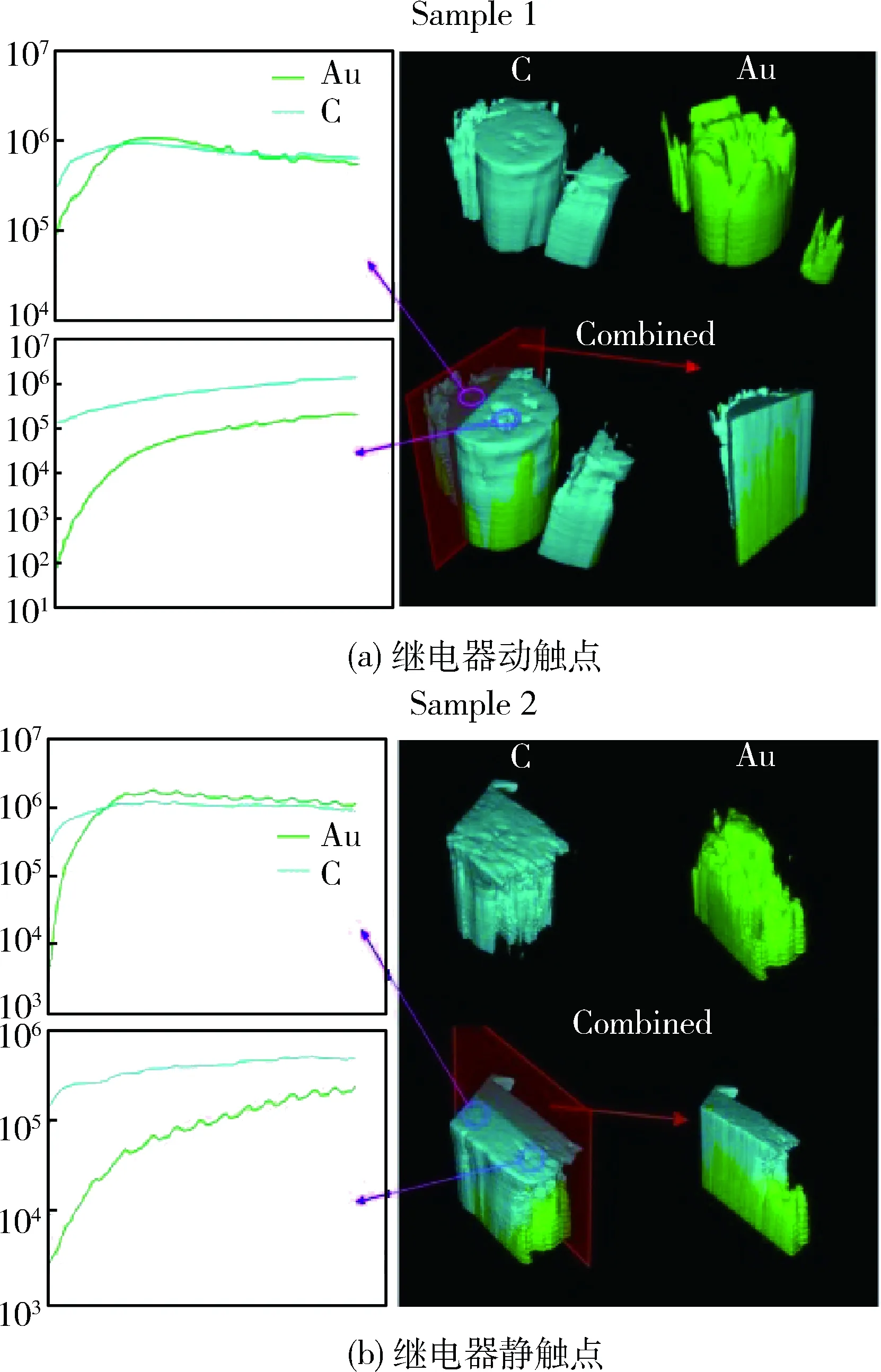
图3 动静触点表面特定元素分布图
由图3可知,动、静触点相对平坦区域的Au和C原始计数率相对数据相当,而凹坑处的C含量明显大于Au含量,这说明Au在微动过程中容易被磨损,烧蚀处容易粘着碳颗粒。
2.3 微量元素分析
虽然是密封式继电器,但是在生产前期过程中可能会引入若干微量污染物质,在继电器工作过程中会析出有害成分,这些会造成触点表面成分的变化。在触点周围介质中以蒸汽状态存在的有机物质吸附在触点表面,并在化学吸附作用下形成有机层。
触点在制造过程中,经高温成型,触点表面部分污染C与基底材料发生化学反应,生成稳定的碳化物,沉积在触点表面。在触点的不断吸合过程中,伴随有电弧现象,电弧会将部分沉积物烧为碳,碳化物在触点闭合过程中也会引燃电弧,循环往复,绕线塑料和底盘塑料分解得到的碳氢化合物便会吸附在触点表面。表面膜上的C和O成分形成可以用一下化学式解释:
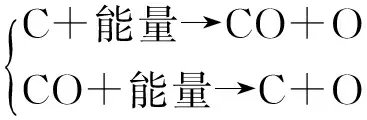
(6)
动触点表面元素含少量P,P的来源可能和松香/焊料有关。氧化物、硫化物等非有机污染主要是金属触点与部分气体化学反应的产物,也包括水和制造过程中的某些金属蒸汽沉积,这些物质大部分导电性都很差,有的还会形成不易破坏的暗膜,或形成微小溶池,加剧触点侵蚀,使接触电阻增大。在长期贮存的继电器密封性出现问题时,大气里的水汽、腐蚀性气体等通过镀层的微裂纹、小孔,利用微管毛细作用渗入并接触到基体金属并沉积下来后,接触表面会形成电解液。当Au和极少的Ag之间可以形成原电池,触点表面发生氧化还原反应,形成氧化物或者硫化物的堆积:
(7)
3 触点组接触面还原
3.1 接触电阻模型
接触电阻的计算一直以来都是电接触研究的一个重要课题。R.Holm最早建立了Holm接触电阻模型,之后也有学者在Holm基础上提出了考虑多斑点、表面膜、温度等因素的更加符合实际接触情况的接触电阻模型,但是这些接触电阻计算公式很难直接应用到实际工程设计中。
对于触点这类粗糙表面而言,实际接触面积取决于负载的大小和2个接触表面的表面形貌。2个粗糙表面实际接触的并不是整个接触表面,而是一些微凸体之间的接触,从而形成离散的接触点或微小的接触面,这些接触点和接触面就构成了实际接触面积。要得到粗糙接触面的实际接触面积,还需要根据实际接触时的表面形貌分析得到接触斑点的个数和半径才能针对触点进行定量计算。
样本继电器触点接触时的三维几何模型如图4(a)所示。不管是哪种材料导体的接触,接触面之间都存在接触表面的不连续性,但是粗糙表面的微凸体的变形存在连续性。两个粗糙表面的接触可以用一个等同粗糙表面和一个刚性光滑表面接触来代替[11]。简化动静触点表面的接触变形关系如图4(b)所示,其真正的接触区域是在微凸体相对较高的顶部区域。
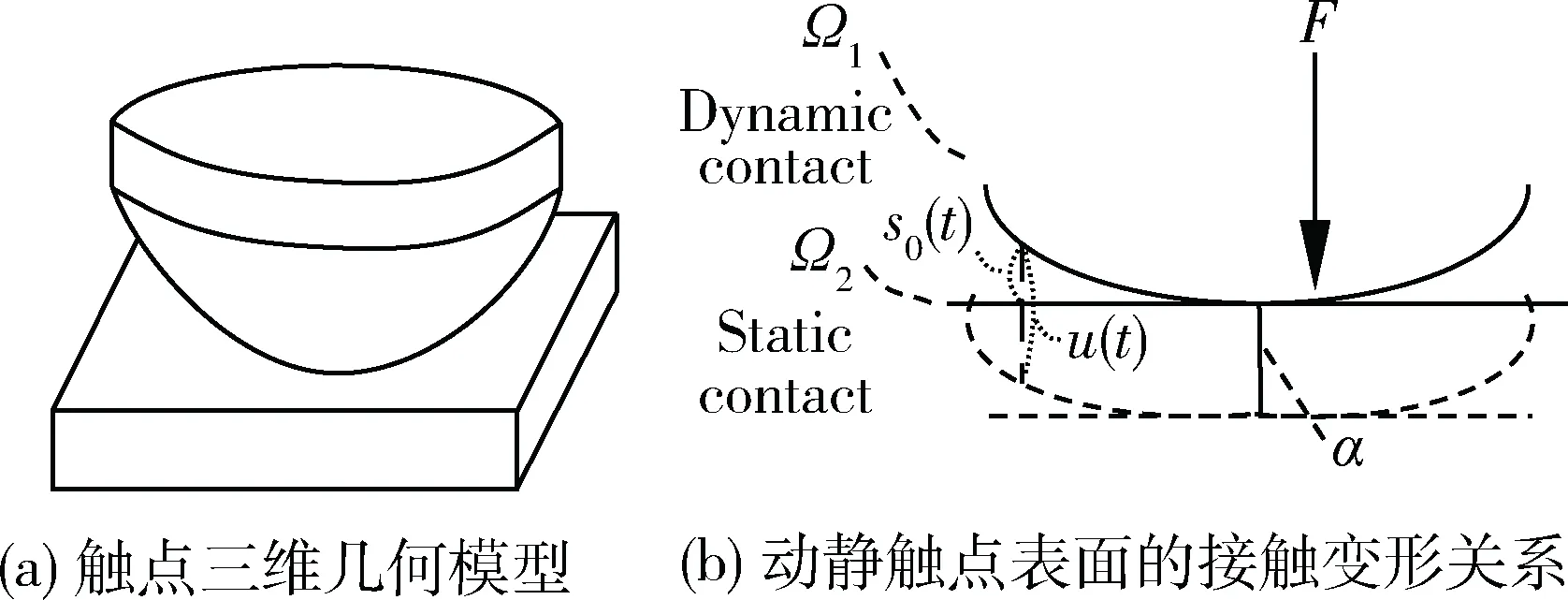
图4 触点三维模型及假设模型
本文基于粗糙表面微凸体变形的连续性和光滑性原理,寻找应力和形变关系。当2个接触面Ω1和Ω2在力F的作用下发生接触时,存在如下关系[3]:
(8)
式中,u(x)是2个物体接触表面的变形位移,即形变量;s0(x)是2个物体的初始间隙,它们都是空间坐标x的函数;α是接触体中心的刚体平动位移。
3.2 触点组表面形貌还原
三维非接触式扫描仪按照线扫描方式扫描触点表面建立基准面,在同一基准面的基础上记录触点表面的高度,扫描得到的数据量足以完全反应继电器触点表面形貌。本文利用三维非接触式扫描仪扫描时,动触点和静触点所处的方位一致,在此基础上用MATLAB还原出的触点真实表面形貌都是接触面方向向上的图形。
考虑到触点在动作过程中是接触状态,当两金属表面互相接触时,最高的粗糙峰顶最先接触。通常会出现较大的局部应力,使接触点产生很强的压缩作用,并使新的粗糙峰顶参与接触,承受大部分荷载。当接触的粗糙峰顶数增加足以承受所施加的荷载时,接触过程才最终完成。在此基础上,本文假设触点的2个接触表面为弹性表面,提出用动静触点表面差平面作为建立接触电阻模型的基础。
为了更好地模拟动静触点的接触过程,按照图1选定触点对应的接触区域,保证选定区域的矩阵大小相同,还原动静触点的三维形貌如图5所示。
先根据继电器触点接触的位置调整好动静触点的接触面,以动触点为相对参考平面,将静触点进行镜像对称。MATLAB读取图5(b)所示粗糙平面的三维坐标,利用镜像变换矩阵对表面进行镜像对称:

(9)
其中,a,b,c为镜像线ax+by+c=0的系数。
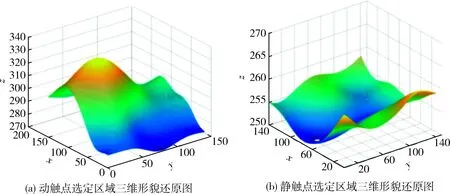
图5 触点选定区域三维形貌还原图
得到图5(b)的镜像图后,计算动触点和静触点镜像图后对应高度之和,以动静触点表面高度和的最高值所在的平面作为基准面,计算对应的高度和与最高点的差值,得到一个差平面。这个差平面就是之后建立一定负载、一定压力下触点接触电阻模型的前提。得到的动静触点组粗糙表面差平面如图6所示。

图6 触点组粗糙表面差平面图
图6反映了继电器触点组在接触过程中的表面形貌状况,通过试验可以分析出继电器触点在运动过程总的负载大小以及触点组之间的压力大小,压力与接触表面的形变量息息相关。建立形变量和差平面的对应模型,可以得到触点接触时的实际接触面积,由此建立触点接触电阻模型。
4 结论
对触点表面进行了形貌和失效分析,提出差平面概念还原触点接触面,从三维表面差平面研究动静触点真实的接触状况,打破用仿真软件仿真模拟接触过程的局限性,对从微观层面建立触点接触电阻模型进一步研究具有一定的指导作用。
后期将着重研究通过试验分析继电器触点在运动过程中总的负载大小以及触点组之间的压力大小,建立形变量和差平面的对应模型,从而得到触点接触时的实际接触面积以及接触电阻模型。
[1] 徐富春,王水菊,汤丁亮,张棋河,林秀华,陆宁懿. 电磁继电器触点表面的SEM和XPS研究[J]. 厦门大学学报(自然科学版),2001,40(4):857-861.(Xu Fuchun, Wang Shuiju, Tang Dingliang, Zhang Qihe, Lin Xiuhua, Lu Ningyi. Studies on Contact Points Wear of Electromagnetic Relay by SEM and XPS[J].Journal of Xiamen University (Natural Science), 2001, 40(4): 857-861.)
[2] 汪久根,冯兰兰,李阳. 粗糙表面形貌对电蚀的影响[J]. 浙江大学学报(工学版),2015,49(11):2025-2032.(Wang Jiugen, Feng Lanlan, Li Yang. Influences of Surface Topography on Electrical Pitting[J].Journal of Zhejiang University (Engineering Science), 2015, 49(11): 2025-2032.)
[3] Liu H, Leray D, Colin S, et al. Finite Element Based Surface Roughness Study for Ohmic Contact of Microswitches[C]. 2012 IEEE 58th Holm Conference on Electrical Contacts (Holm). IEEE, 2012: 1-10.
[4] 炊明伟,冯有前,王崴,李正朝,徐晓东. 改进中值滤波和最小二乘法在三维表面评定中的应用[J]. 表面技术,2012,41(6):118-121.(Chui Mingwei, Feng Youqian, Wang Wei, Li Zhengchao, Xu Xiaodong. The Application of the Improved Median Filter and Least Square Method in Evaluation of 3D Surface Topography[J]. Surface Technology, 2012, 41(6): 118-121.)
[5] Liao Y, Stephenson D A, Ni J. Multiple-Scale Wavelet Decomposition, 3D Surface Feature Exaction and Applications[J].Journal of Manufacturing Science and Engineering, 2012, 134(1): 011005.
[6] 李小兵,王清华.基于多尺度理论的三维表面形貌表征研究[J]. 机械设计与研究, 2014, 30(2): 119-120.(Li Xiaobing, Wang Qinghua. Research of Multi-scale Theory in the 3-D Surface Morphology Characterization[J].Machine Design and Research, 2014, 30(2): 119-120.)
[7] 张程宾,陈永平,施明恒,付盼盼,吴嘉峰. 表面粗糙度的分形特征及其对微通道内层流流动的影响[J]. 物理学报,2009,58(10):7050-7056.(Zhang Chengbin, Chen Yongping, Shi Mingheng, Fu Panpan, Wu Jiafeng. Fractal Characteristics of Surface Roughness and Its Effect on Laminar Flow in Microchannels[J].Acta Physica Sinica, 2009,58(10): 7050-7056.)
[8] Yan W, Komvopoilos K. Contact Analysis of Elastic-plastic Fractal Surfaces[J].Journal of Applied Physics,1998,84(7):3617-3624.
[9] 朱纪磊,汤慧萍,奚正平,邸小波. 多孔结构分形分析及其在材料性能预报中的应用[J]. 稀有金属材料与工程,2009,38(12):2106-2110.(Zhu Jilei, Tang Huiping, Xi Zhengping, Di Xiaobo.Fractal Analysis of Pore Structure and Its Application for Prediction of Permeability and Porosity[J]. Rare Metal Materials and Engineering, 2009,38(12): 2106-2110.)
[10] 李成贵,张国雄,袁长良. 分形维数与表面粗糙度参数的关系[J]. 工具技术,1997,31(12):36-38.(Li Chenggui, Zhang Guoxiong, Yuan Changliang. The Relationship Between the Fractal Dimension and Surface Roughness Parameters[J]. Tool Technology, 1997,31(12): 36-38.)
[11] 赵永武,吕彦明,蒋建忠. 新的粗糙表面弹塑性接触模型[J]. 机械工程学报,2007,43(3):95-101.(Zhao Yongwu, Lv Yanming, Jiang Jianzhong. New Elastic-plastic Model for the Contact of Rough Surfaces[J]. Chinese Journal of Mechanical Engineering, 2007, 43(3):95-101.

