基于降阶ESO的微小型空地导弹滚转变结构控制

钟高伟 陈东生 王明光

北京航天微系统研究所，北京100094

现代及未来战场无人机携带攻击型微小型空地导弹已成趋势，为了进一步提高作战能力及打击精度，配备捷联、框架式导引头的微小型空地导弹需在投弹后极短时间内将滚转角稳定在0°范围左右，以防止导引头输出目标信息不准确；另一方面，滚转角稳定控制能减少姿态三通道间的强耦合，进一步提高制导精度。

对于弹翼展弦比小的轴对称微小型空地导弹来说，其滚转转动惯量很小，由其结构特性进一步计算可知，滚转通道被控对象的时间常数及增益很小，导致采用基于二回路的经典控制论的滚转通道鲁棒及抗扰能力差。此外，复杂多变的飞行环境带来的模型高度不确定性及外部阵风干扰，以及自身内部强扰动等因素的存在，使得应用经典控制论或其改进型更加力不从心，很难满足工程所需的控制要求。

各国对此类微小型导弹的控制技术处于保密封锁阶段，微小型导弹滚转控制的研究文献并不多。但是，常规型空地导弹如BTT导弹滚转控制研究已取得一定的研究成果，不妨可以将其作为参考。目前在国内研究中，文献[1]中，宋金来等人采用自抗扰技术中核心思想ESO，利用观测器将系统的总和扰动估计，并进行实时补偿，简化了被控对象，方便后续PD控制器设计；文献[2-3]中，研究人员将神经网络分别与自适应及动态逆等鲁棒控制相结合，改善了控制的动态性能，既减弱了模型不确定性也削弱了神经网络对跟踪误差带来的不利影响；文献[4-5]中，研究人员利用模型参考自适应鲁棒控制及模糊算法智能控制去优化变结构控制，改善其抖振现象及平衡点收敛慢等缺点，能保证快速响应且稳定跟踪指令；文献[6-7]中，杨军等提出参数空间法设计准则将其应用并设计出制导炸弹滚转通道控制器，实现大动压范围内制导炸弹稳定控制，具有良好的鲁棒性。在国外研究中，文献[8-9]中，Huang S J等借助神经网络逼近设计了基于REF网络的滑模控制器，Zhang C F等采用遗传算法进行切换函数的优化，将抖振的大小作为优化适应度函数的重要指标，构造了抖振最小的切换函数。

鲁棒控制复杂的控制公式难以编程应用，传统变结构控制中抖振及奇异问题使得执行机构如舵机等易于损坏；智能控制的应用虽然减弱了不确定性，优化了控制参数，但是其离线计算及较为复杂的迭代过程限制了工程实时计算的要求；参数空间法等现代控制论不具备整套完整的稳定裕度分析及经典控制论的鲁棒及抗扰能力差。基于以上原因，本文结合降阶ESO[10-11]及非奇异终端滑模变结构控制，提出一种复合控制方法来实现闭环系统误差有限时间收敛，提高其鲁棒性及抗干扰能力，并有效减弱抖振。首先，采用非奇异滑模面设计变结构控制器能使系统在有限时间内稳定，特别是在平衡点具有更好的收敛性能，保持较好的参数摄动抑制能力；其次，利用降阶ESO对被控对象未建模内扰及外部干扰实时估计，将估计值作为前馈量补偿给控制输入端，以此削弱未建模部分及干扰带来的抖振；采用基于超螺旋算法的鲁棒微分器[12]处理指令信号，既作为滤波器也为微分器，便于工程实现。

1 滚转通道数学模型

导弹滚转姿态动力学方程[13]可简化表示为

(1)

式中，Jx，Jy和Jz分别为滚转、偏航和俯仰的转动惯量；ωx，ωy和ωz分别为弹体角速度在弹体坐标系中的分量；q为动压；Sref为弹体参考面积；Lref为参考长度；mx为滚转力矩系数。

令滚转力矩为Mx=mxqSrefLref，则由气动特性及结构特征，可具体表征为

(2)

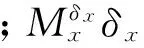
(3)

(4)

式中，b11为滚转阻尼系数；b17为滚转舵效系数；b18ΔM可视为内部总和扰动。

根据线性关系，滚转舵到滚转角速度的传递函数为

(5)

2 微小型空地导弹滚转特性分析

空地导弹由长度及重量常分为大型、中型、小型及微小型，本文研究对象是微小型空地导弹，以某具体研制型号为背景，气动外形为轴对称正常式布局。通常来说定义微小型导弹弹体长度小于1.5m，重量低于15kg，这与其余类型同气动外形的弹体在动力学模型上保持一致，且气动参数可视为一致，差异在于结构特性的不同，即转动惯量Jx，气动参考长度Lref及气动参考面积Sref。故计算出的模型参数b17和b11数值差异明显，依据经典控制理论设计的控制参数也会有所不同，以例1为特征点具体分析。

2.1 被控对象模型对比

表1 气动、结构参数

将模型参数代入式(5)可以得到2者传递函数分别为

2.2 经典PID设计

通常微小型空地导弹滚动控制回路一般采用二回路姿态控制，如图1所示，即内回路是角速率反馈的阻尼回路，其反馈系数为Kω；外回路采用基于角位置反馈的控制回路，为了使控制回路具有充裕的裕度及较好的控制品质，控制器采用“比例控制为主，积分控制为副”的控制策略，即PI控制。

图1 PI控制回路图

根据反馈控制理论，Kω越大，越能抑制被控对象的不确定性和外部扰动对控制品质的影响，其设计原则是在控制裕度允许的情况下，Kω尽可能取较大的值。Kω的上限取决于滚转控制回路的带宽，设控制回路的截止频率为ωc，则

(6)

采用例1设计控制回路，设计外回路的截止频率为4rad/s，由设计原则得阻尼回路Kω分别为0.0014和0.0342。忽略测量机构，得到内回路阻尼回路的传递函数

Kω=0.0014；

Kω=0.0342；

由上式可知，阻尼反馈系数Kω相差近24倍。继而设计并调试出前向串联PI控制参数，满足阶跃响应的稳定性和快速性要求，得到PI参数，见表2。

表2 PI控制参数

2.3 微小型导弹的“怪异”表现

基于二回路的控制回路设计完毕后，通过计算及仿真，可以得到两者开环频率特性如表3所示，时域响应由图2所示。

表3 稳定裕度

图2 滚转角响应

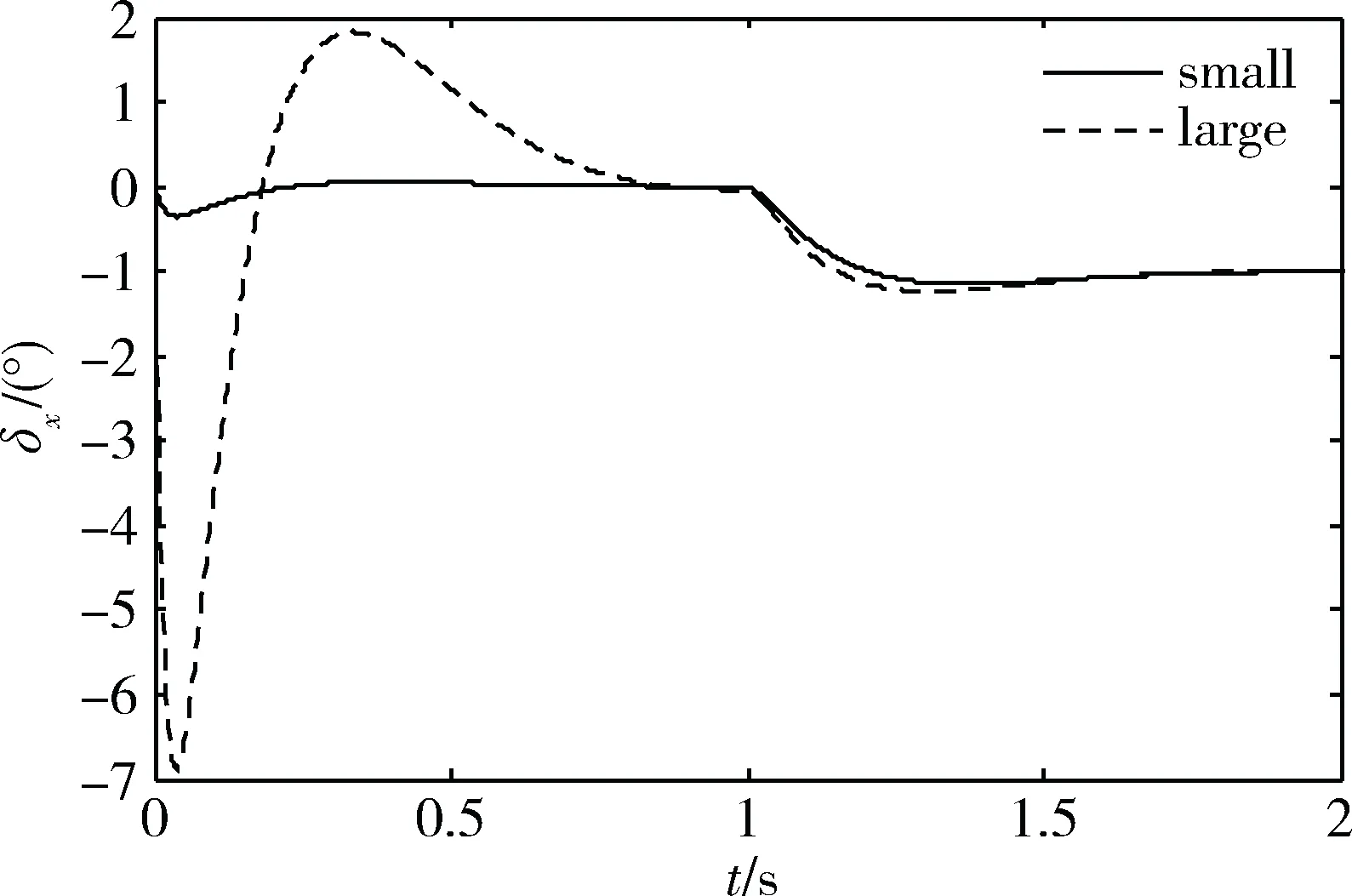
图3 滚转舵偏

当弹体在1s后受到一个相当于1°滚转量级的干扰力矩时，其闭环阶跃响应如图2所示，两者控制舵偏变化如图3所示。由此可以看出，设计并调试出的参数在满足控制系统稳定裕度指标的前提下，使得两者的闭环传递函数一样，故两者开环的截止频率、相位裕度以及幅值裕度几乎完全一致，其差别在于微小型导弹的3个控制参数取值较常规型导弹小得多，尤其是Kω反馈阻尼参数。由反馈控制论可知，阻尼参数小，抑制不确定性及抗扰动能力弱。因此，在未出现干扰，时微小型导弹和常规型导弹在响应指令信号能力上几乎一样，一旦出现外界的扰动，微小型导弹大幅脱离指令信号，而常规型导弹能快跟踪上指令信号。

3 非奇异终端滑模变结构控制器

由式(4)简化并忽略耦合影响，得到滚转二阶模型

(7)

式中，x1为滚转角；x2为滚转角速度；u为控制舵偏量即δx。由于b11ωx自身阻尼项数值小且难以得到精确值，故将其并入内部干扰项b18ΔM中。在外界干扰存在的情况下，将内外复合干扰表示为d(t)。

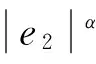
(8)

式中，β1>0，1<α=a/b<2，且a，b为奇数。

(9)

式中，k>0，σ>0，0<η<1。

由式(7)～(9)得到控制律为

(10)

由式(10)可知，系统未建模部分、内部扰动及外界干扰在d(t)中得以体现。因此，如何快速估计出d(t)是控制器设计的关键。

4 降阶ESO设计

由文献[10]及文献[11]可知，在某些状态量可测的情况下，线性降阶ESO更为实用，与非线性ESO相比，结构简单，其中的参数与实际工程中的带宽概念相匹配，这非常有利于参数的调试与系统带宽的匹配。

考虑微小型导弹滚转通道滚转角可测，将式(7)改写为

(11)

式中,x1为滚转角速度;x2为复合干扰d(t)。

由文献[10]可知，结合式(11)，得到滚转通道的降阶ESO设计式

(12)

对式(11)和(12)进行拉式变换，化简可得

(13)

由此可见，降阶ESO可以视为一阶惯性环节，其时间常数β-1即为观测器带宽。通过选择合理的β搭配系统闭环带宽满足工程要求。

5 基于超螺旋算法的鲁棒微分器

由于采用非奇异终端滑模控制，设计的滑模面以及得到的控制量需要输入的指令信号的一阶、二阶微分，且还能对输入信号进行滤波，故采取鲁棒微分器[12]的方式满足此要求。鲁棒微分器既可以作为观测器使用也可以作为微分器使用。

(14)

6 闭环系统稳定性分析

降阶ESO及控制器设计完毕后，在指令信号输入端加入鲁棒微分器，得到整个闭环回路控制图，见图4。

图4 复合控制结构图

(15)

将式(10)代入式(15)，可得

(16)

为了说明闭环的稳定性，给出如下假设和定理。

假设1 假设d(t)，即d(t)是有界的并存在一个常数D>0，则有|d(t)|≤D。

定理1 若假设1满足，且合理选择降阶ESO的增益β1，那么观测器的误差e0指数收敛并且有界，且收敛域为

式中，ωc为观测器带宽，其值等于β1。

考虑降阶ESO式(12)、滑模面式(8)与控制量式(10)作用下闭环系统的收敛特性。针对滚转通道式(7)，构造如下的正定Lyapunov函数

(17)

对式(17)求导，可得

(18)

又有-ks2≤0，所以上式可改写为

(19)

随着t→∞，s→0，e0收敛到0，且β1>0，α>1，k>0，σ>0，η>1,式(19)变为

(20)

满足滑模面到达条件，因而闭环控制系统稳定。

由有限时间稳定定理可知，随着V的减小，闭环系统的轨迹满足

(21)

且能在有限时间收敛到滑模面邻域。同时，有限收敛的时间可表示为

(22)

综上所述，在降阶ESO稳定的情况下，通过调试控制参数k，σ，α,可以保证系统的轨迹在有限时间内收敛于s=0的邻域内，即状态量x1滚转角能跟踪上指令滚转信号，但存在稳态收敛误差。稳态误差的误差收敛域与观测器的误差存在正比关系。

7 数值仿真

通过与经典控制设计滚转通道控制器即二回路控制法进行对比。首先，选取例1条件为特征点，进行非奇异变结构控制器及降阶ESO的调参。选取一组合适参数：鲁棒微分器中C=5，k0=1.1C，k1=4C1/2，k2=8C1/3；降阶ESO中β=10；非奇异变结构控制器中k=18，σ=5，η=0.5，β=0.1，α=17/15。定义式(6)中内部总和干扰为f=5sin(t)，并在5～10s内加入一个近似1°的滚转干扰力矩。另外，仿真时给系统加入50ms的延迟，以此测试控制回路抗延时特性。

由图5～6可知，鲁棒微分器能满足微分、滤波及观测的作用，但是在噪声污染较为严重时，其二阶微分信号变得很差，存在严重的相位滞后现象，且微分及滤波效果对参数较为敏感，参数的改变不光影响估计精度，而且还会给系统带来延时。

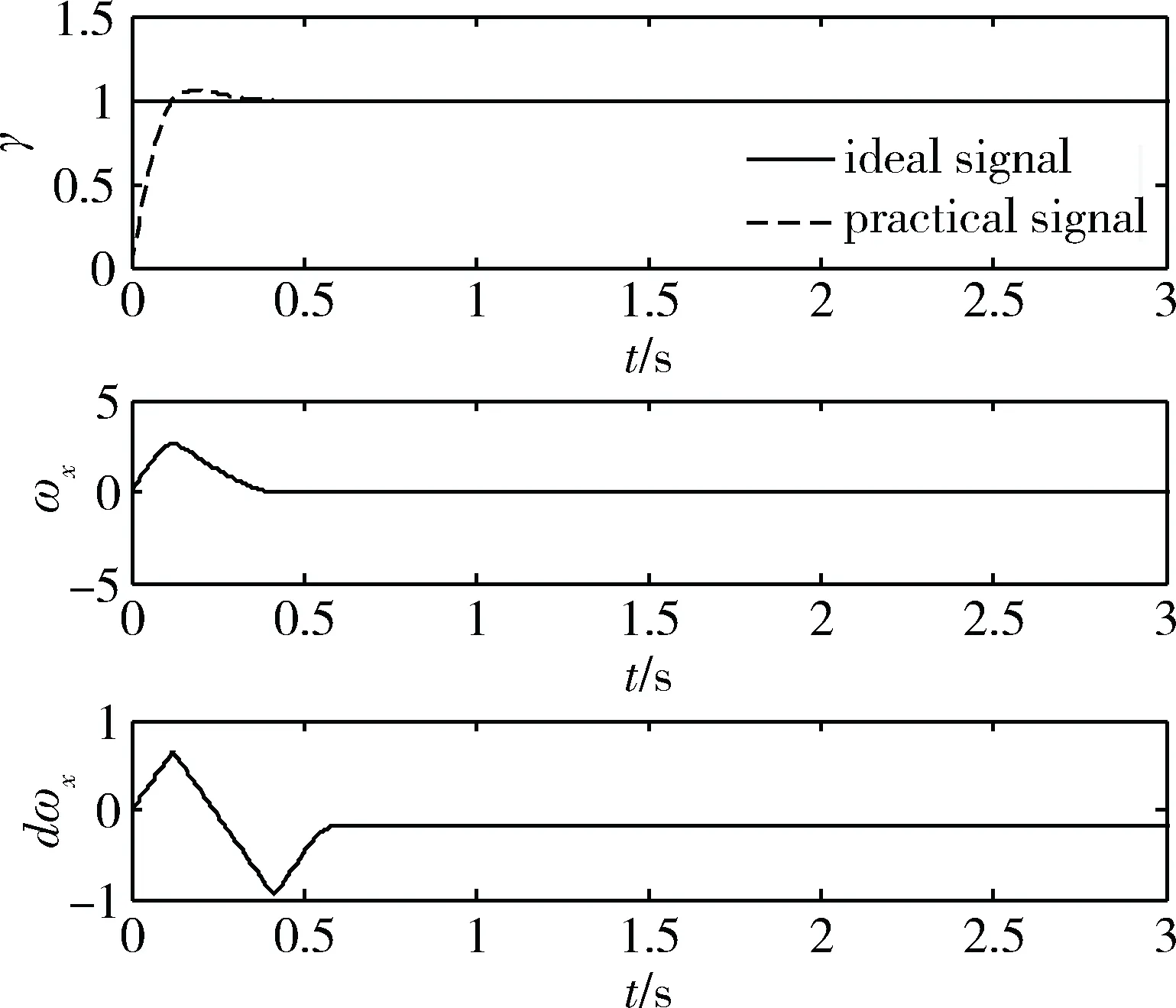
图5 无噪声污染估计信号

图6 噪声污染估计信号

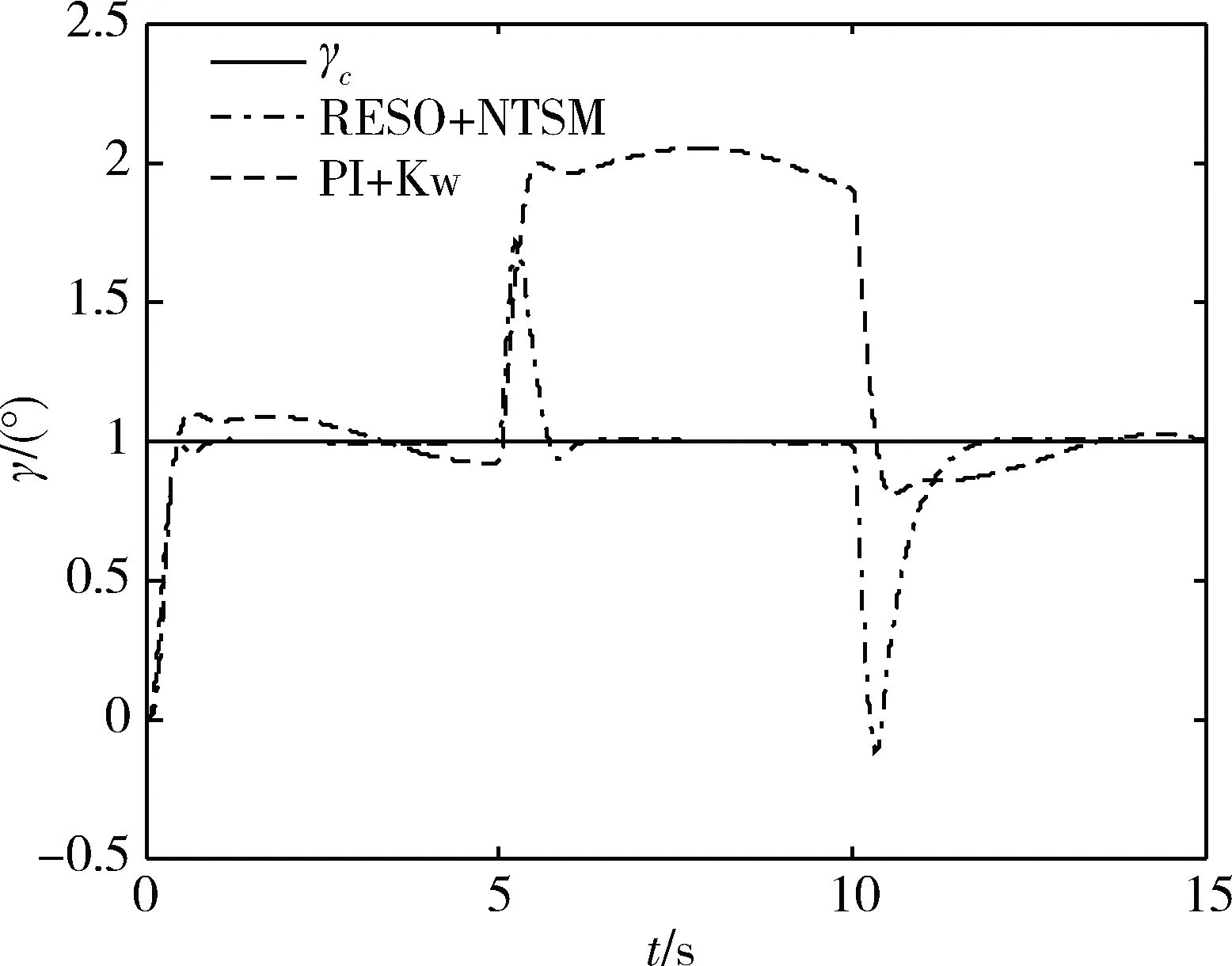
图7 滚转角响应

图8 不同kc值下指数趋近律相轨迹趋近过程

图9 降阶ESO估计“总和干扰”

图10 控制舵偏量

由图8可知，滑模面中k的不同取值会影响滑模收敛时间及收敛过程，但最终状态都会收敛到滑模面0点平衡处，相较于传统的非奇异终端滑模控制，具有快速收敛特性，且通过图10可知，控制量在平衡点处抖振现象得到抑制。图9显示选择合理的参数，降阶ESO能很好地估计出“复合干扰”，观测器带宽及精度随着参数增大而增大，但是参数的增大也会给系统带来延迟、相位滞后，使得系统稳定性降低。由图7～10可知，经典控制论设计出的控制器在未出现干扰时，稳定裕度及响应指标都满足设计要求，但是一旦出现外界干扰和内部扰动，控制器性能急剧下降，近乎无抗干扰能力。对于智能控制结合滑模变结构的控制方法，从本质上来说，只是出于优化参数及降低抖振现象而存在，并未提升系统鲁棒及抗扰动性。因此，本文的核心降阶ESO的存在使得复合干扰得以估计并补偿入控制输入端，再进而采用变结构控制使得对象能够短时间内跟踪上指令信号，且抑制模型参数不确定性摄动。另外，由图10中可看出复合控制能迅速给出平稳控制舵偏量，以此来控制舵面偏转，抖振现象也得以抑制。

8 结论

针对微小型空地导弹滚转通道在经典控制论设计出的控制器下出现的局限性，设计了基于降阶ESO的非奇异终端滑模变结构控制方法。首先，采用降阶ESO估计出系统的“复合干扰”，并将其实时补偿到控制输入端。其次，设计非奇异终端滑模控制能够保证系统稳定跟踪指令，且跟踪误差能在有限时间内收敛。两者结合形成的复合控制，不仅能稳定跟踪指令信号、抑制参数不确定性摄动以及提升系统抗干扰能力，而且变结构控制伴随的抖振现象也得以抑制。

[1] 宋金来，金岳. 制导炸弹滚转通道自抗扰控制设计方法研究[J]. 航天控制，2014，32(11)：26-39.(Song J L，Jin Y. Research of Active Dsiturbance Rejection Control for Guided Missile Control[J]. Aerospace Control. 2014，32(11)：26-39.)

[2] 黄树彩，李为民. BTT导弹的神经网络自适应非线性自动驾驶仪设计[J]. 宇航学报，2007，(5)：1232-1234.(Huang S C，Li W M. Design of Neural-Adaptive Nonlinear Autopilot for BTT Missile[J]. Journal of Astronautics，2007，(5)：1232-1234.)

[3] 杨志峰，雷虎民，李庆良，李炯. 基于RBF神经网络的导弹鲁棒动态逆控制[J]. 宇航学报，2010，(10)：2296-2301.(Yang Z F，Lei H M，Li Q L，Li J. RBF Neural Network Based Robust Dynamic Inverse Control for a Missile[J]. Journal of Astronautics，2010，(10)：2296-2301.)

[4] 汤柏涛，董斌，于云峰. BTT导弹滚转通道模型参考变结构自动驾驶仪设计[J]. 计算机测量与控制，2011，(1)：105-107.(Tang B T，Dong B，Yu Y F. Autopilot Design for BTT Missile Based on Mode Reference Variable Structure Control[J]. Computer Measurement & Control，2011，(1)：105-107.)

[5] 梁卓，薛晓中，孙瑞胜，王航. 制导炸弹模糊变结构滚转自动驾驶仪设计[J]. 战术导弹技术，2010，(3)：78-82.(Liang Z，Xue X Z，Sun R S，Wang H. The Design of Guided Bomb Fuzzy Variable Structure Rolling Autopilot[J]. Tactical Missile Technology，2010，(3)：78-82.)

[6] 杨军. 参数空间方法与飞行控制系统[M]. 北京：航空工业出版社，2008.(Yang J. Parameters Space Methods and Flight Control Systems[M]. Beijing：Aviation Industry Press.)

[7] 许友竹，凡永华. 制导炸弹滚转通道控制方法研究[J]. 科学技术与工程，2012，(1)：526-529.(Xu Y Z，Fan Y H. Research on Control Methods of Guided Bomb Rolling Channel[J]. Science Technology and Engineering，2012，(1)：526-529.)

[8] Huang S J，Huang K S，Chou K C，Development and Application of Novel Radial Basis Function Sliding-mode Controller[J]. Mechatronics，2003(13)：313-329.

[9] Zhang C F，Wang Y N，He J，GA-NN-Integrated Sliding Mode Control System and Its Application in the Printing Press[J]. Control Theoty & Applications，2003,20(2)：217-222.

[10] 韩京清. 自抗扰控制技术[M]. 北京：国防工业出版社，2013.(Han J Q. Active Disturbance Rejection Controler，ADRC[M]. Beijing：National Defense Industry Press，2013.)

[11] 薛文超. 自抗扰控制的理论研究[D]. 北京：中国科学院研究生院，2012.(Xue W C. Theoretical Study on Active Disturbance Rejection Control[D]. Beijing：Graduate University of Chinese Academy of Sciences，2012.)

[12] Levant A. Robust Differentiation via Sliding Mode Technique[J]. Automatica，1998，34(3).

[13] 钱杏芳，林瑞熊，赵亚男. 导弹飞行力学[M]. 北京：北京理工大学出版社，2012.(Qian X F，Lin R X，Zhao Y N. Missile Flight Aerodynamics[M]. Beijing：Beijng Institude of Technology Press，2012.)

[14] 刘金琨. 滑模变结构控制MATLAB仿真基本理论与设计方法[M]. 北京：清华大学出版社，2015.(Lin J K. The Design Method of Sliding Mode Variable Structure Control Matlab Simulation[M]. Beijing：Tsinghua University Press，2015.)