抓捕航天器的多环递归姿态跟踪控制*
殷春武
1. 西安建筑科技大学信息与控制工程学院,西安 710055 2. 西北工业大学自动化学院, 西安 710129
伴随空天活动的增多,火箭箭体的喷射物、航天任务的抛弃物以及空间物体之间碰撞产生的碎片等太空垃圾的数量,每年呈指数增长,严重威胁着航天器和出仓航天员的安全,抓捕并回收太空垃圾成为急需解决的关键课题。动力特性未知的空间碎片(也称为非合作目标)在太空中呈无序飞行,抓捕空间碎片过程中,抓捕航天器的姿态及其姿控系统的参数会产生摄动,为保障抓捕航天器的安全,抓捕航天器的姿态必须快速、精确地收敛到期望姿态。
刚体航天器的鲁棒姿态控制研究起步较早,主要集中在抗干扰控制和转动惯量摄动控制[1-3]。具有强鲁棒性的滑模控制能有效解决转动惯量摄动上界已知条件下的姿态稳定控制问题,但滑模控制容易导致控制力矩出现抖振。当转动惯量摄动上界未知时,需要借助自适应更新律或智能逼近来估计未知转动惯量,并建立基于转动惯量估值的非线性控制器,但自适应更新律不能实现对转动惯量的精确估计,智能逼近器则能逐渐逼近实际转动惯量[4-7]。抓捕航天器在抓捕非合作目标过程后,将与非合作目标组成新的复合体,抓捕航天器的质量和转动惯量将会发生突变。因此,抓捕航天器的鲁棒姿态控制算法,不仅要对渐变的参数摄动和外部干扰具有强鲁棒性,还必须能有效克服姿态系统的参数突变。
受执行器输出能量的限制,实际执行器的输出幅值是有限的。早期的饱和控制策略是,先不考虑控制饱和约束,设计姿态控制器,再采用符号函数或饱和函数对控制器的输出进行限幅,系统实际控制输入达不到理论输入,容易导致系统的不稳定。理论分析可知,当事后限幅时,限幅后的控制输入并不等于所设计的控制器,不能保证闭环系统的稳定性。要使姿态动力学系统在实际工程应用中满足控制饱和约束,就应该在控制器设计过程中(即事中)考虑饱和约束,并从理论上分析所设计姿态控制算法能保证闭环系统的稳定性[8-12]。本文将在控制器设计过程中考虑控制饱和约束,利用构建辅助预测系统预测控制饱和超幅部分,设计多环递归跟踪控制器,并从理论上证明该控制策略的合理性和有效性。针对姿态动力学系统中转动惯量未知和参数突变的约束,本文将建立基于转动惯量估值的辅助预测系统,并解决了引入基于估值的辅助预测系统后,整个闭环系统的稳定性证明问题。
有学者通过数值对比仿真突出其所设计控制器能有效提高姿态跟踪精度,但缺乏通用性,主要原因是其所提出的控制算法不是从提高控制精度的理论分析上获得。本文通过分析影响姿态稳态误差的主要原因,从理论分析入手提出姿态跟踪控制策略,以提升姿态跟踪精度,降低姿态跟踪稳态误差。
本文的创新之处在于,将姿态跟踪误差的积分项引入姿态跟踪误差动力学系统,将原二阶系统扩展成新的三阶扩展姿态跟踪误差动力学系统,并根据原控制目标给出了扩展系统跟踪控制目标的设计方法。对传统反演控制进行改进,提出多环递归跟踪控制策略,并将其用于抓捕航天器的姿态跟踪控制中。在控制器设计中考虑控制饱和约束,引入基于参数估值的饱和超幅辅助预测系统,并从理论上证明了引入辅助系统后的闭环系统稳定性。
1 抓捕航天器姿态控制问题描述
对刚体抓捕航天器按照yaw-pitch-roll (θ3-θ2-θ1) 进行旋转,则抓捕航天器的姿态运动学方程为[13]:
(1)
存在控制饱和约束的航天器动力学方程:
(2)

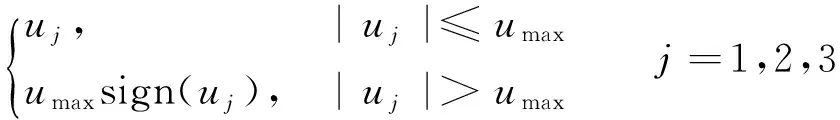
(3)
(4)
(5)
ω×为ω=[ω1,ω2,ω3]Τ的反对称矩阵
(6)
在捕获非合作目标过程中,抓捕航天器的机械臂将执行伸展、抓捕及回收动作。机械臂伸展会导致抓捕航天器的质心逐渐偏移,姿控系统的转动惯量将呈非线性摄动(记为λ1(t)J0);在T0时刻抓捕非合作目标瞬间,非合作目标与抓捕航天器构成新的复合体,抓捕航天器的质量会产生一个瞬间较大增量,等价为转动惯量摄动量为λ2J0;随后,机械臂回收,抓捕航天器的质心发生改变,其转动惯量也将产生一个非线性摄动(记为λ3(t)J0),在T1时刻回收完毕后,转动惯量摄动量稳定在一个固定值上,抓捕航天器完成整个抓捕任务。抓捕非合作目标过程中的姿态系统转动惯量摄动变化模型,可用如下数学模型描述:

(7)

(8)
(9)


(10)
2 抓捕航天器姿态控制器设计
滑模变结构控制是根据系统所期望的动态特性设计切换超平面,控制器根据当前状态以跃变方式不断切换,促使系统状态到达切换超平面,最终实现系统的鲁棒控制。这种通过改变控制器结构的控制方法使不可控系统变为可控系统,且增强了被控系统的鲁棒性,说明改变系统或控制器结构的控制方法能有效改善被控系统的品质。但通过改变系统结构提升控制品质的研究成果并不多见。为了提升抓捕航天器的姿态跟踪精度,减小和消除抓捕非合作目标过程中的姿态跟踪稳态误差,本文尝试利用改变姿态动力学的系统结构实现该目的。
2.1 扩展姿态跟踪误差动力学系统
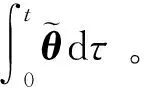
(11)
(12)
2.2 扩展姿态跟踪误差动力学系统的控制目标设置
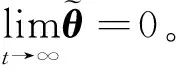
(13)
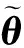
(14)

注1:确定扩展变量的期望轨迹是实现控制器设计的前提,为尽可能的减少控制器中参数的设置,此处给出了一种确定扩展变量期望轨迹的方法,也可以根据实际情况,选择其他方法设计扩展变量的期望轨迹。

(15)
2.3 多环递归姿态跟踪控制器设计
下面针对扩展姿态动力学系统(12),对传统的反演控制方法进行改进,提出一种自适应多环递归姿态跟踪控制器设计策略,并从理论上证明该控制策略能保证闭环系统的渐近稳定性。其控制结构图如图1所示。
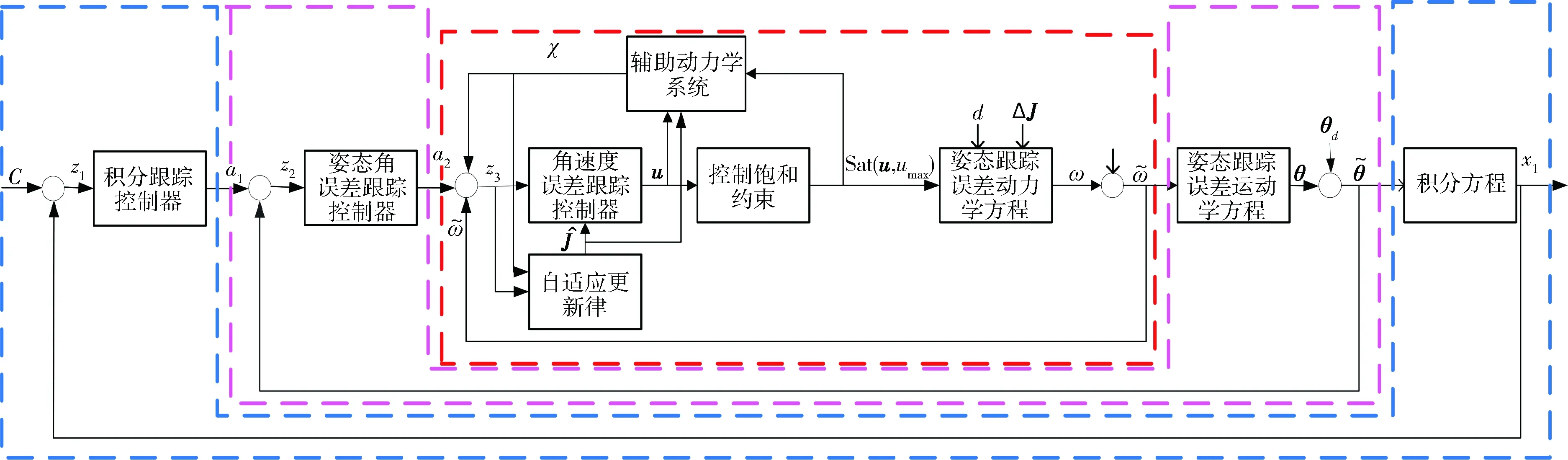
图1 多环姿态跟踪控制器结构图

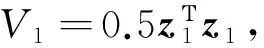
(16)
设计扩展跟踪器为
α1=-k1z1
(17)

(18)
设计姿态角跟踪控制器为
(19)
其中控制增益k2>0。

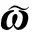
(20)
其中,增益k4>0用来调整变量χ的收敛速度。


(21)
则等式(22)成立:
Ja=L(a)ξ
(22)
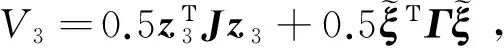
(23)
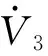
(24)
则有
(25)
(26)
(27)
其中,控制增益k3>0。将式(26)、(27)代入(25)有
(28)
2.4 多环递归姿态跟踪控制器的稳定性分析


证明:对式(28)两边积分得
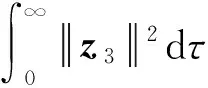
(29)

(30)
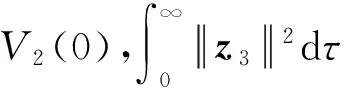
(31)
适当选择常数c2,k1和ε1>0,有
(32)
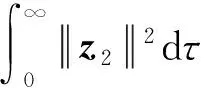
为降低控制输入的抖振,用饱和函数代替符号函数,姿态跟踪控制器式(26)修改为:
(33)
为避免常值增益导致初期控制输入过大,有效平衡控制输入和收敛时间,本文设置如下的时变增益函数调整控制器中的增益系数[5]
ki=ρieαiarctan(βit)i=1,2,3,4
(34)
式中,常数ρi,αi,βi>0。ρi用来调节增益的取值范围;αi调节增益的增长速度;βi调节增益收敛到恒定值的速度;arctan(t)是反正切函数。
3 仿真验证
抓捕航天器初始姿态θ(0)=(20°, -10°,25°),初始角速度为ω(0)=(0.01,0.01,0.01),已知名义转动惯量J0和转动惯量矩阵的摄动量ΔJ分别为:
外部干扰力矩d∈R3为(ωΔ=0.1)

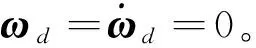
T0=25s,T1=40s,D=1.5,
C=(3.8785,-1.9393,4.8481)
ρ1=0.1,α1=0.9,β1=0.25,
ρ2=0.1,α2=1,β2=0.35,
ρ3=0.5,α3=5,β3=0.25,
ρ4=0.5,α4=5,β4=0.25,
Γ=diag(1,1,1,1,1,1),δ=0.01.
仿真结果见图2~5。 仿真分析结果显示,抓捕航天器在轨捕获非合作目标的过程中,当采用本文设计的多环姿态跟踪控制器(MLATC)时,航天器的姿态角能够快速收敛到期望姿态。整个抓捕过程中,航天器实际姿态角的收敛轨迹几乎呈指数下降,收敛过程中不存在姿态振荡过程,说明该控制器下,抓捕航天器姿态角的调整具有较好的动态品质。航天器姿态跟踪误差在区间[0°,0.02°]范围内,稳态误差非常小,有效提升了姿态跟踪精度。实际角速度的变化范围在区间[0,0.035]rad/s内,小的角速度变化,能有效保证航天器的平稳性,满足抓捕航天器的带宽和角速率陀螺量程限制。控制力矩满足控制饱和约束,所有力矩均没有超过2.5N·m,且力矩不存在抖振现象。
同样的,姿态角和角速度条件选择文献[15]中的滑模自适应姿态控制器(SAAC),当采用饱和函数对文献[15]中的控制输入限幅时,闭环系统是发散的,说明直接对控制器的控制输出饱和限幅并不能保证闭环系统的稳定性,从侧面说明,要保证闭环系统的稳定性,必须在控制器设计过程中考虑控制饱和约束问题。
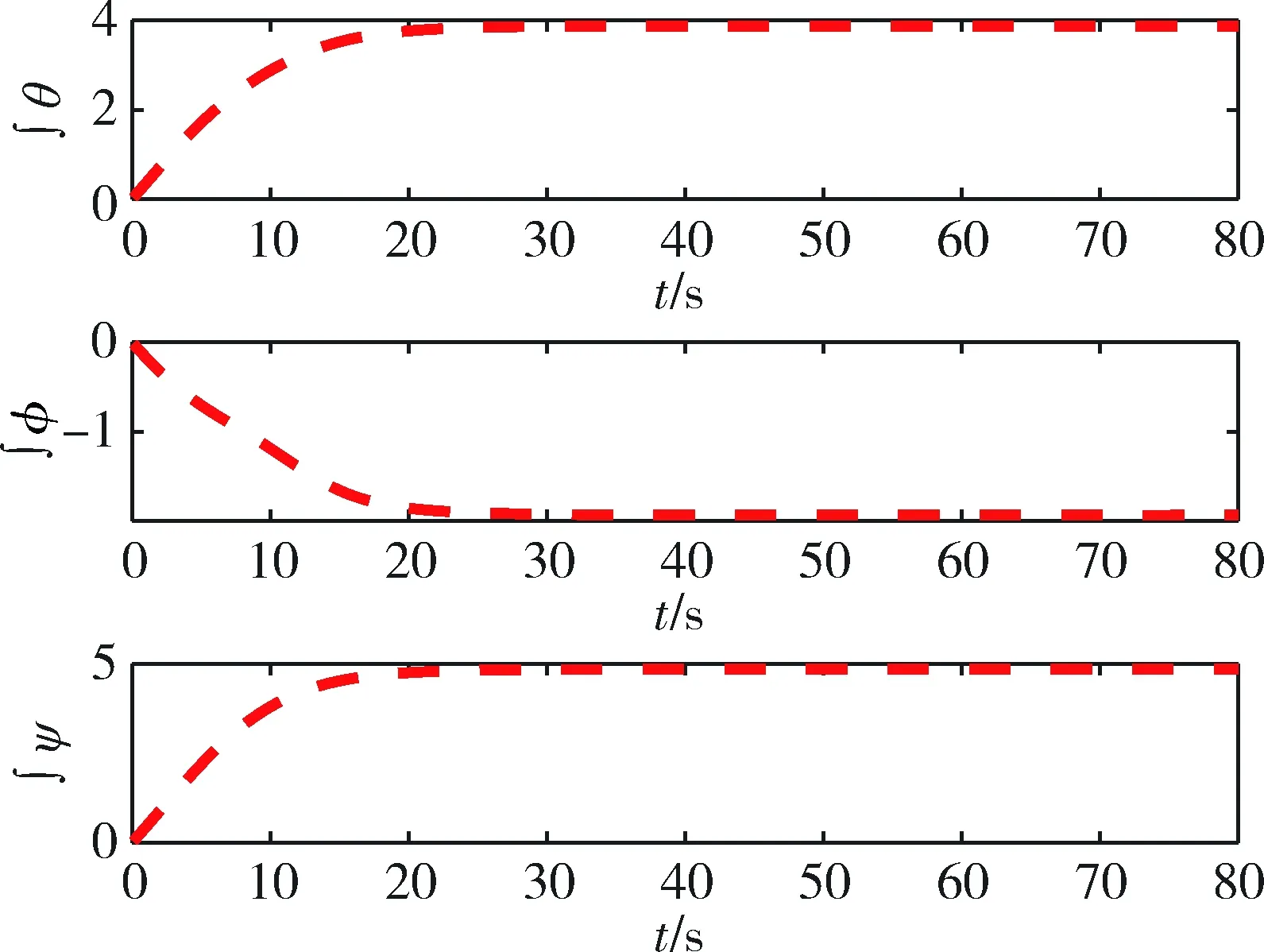
图2 MLATC控制下的积分项变化轨迹

图3 MLATC控制下姿态角跟踪曲线
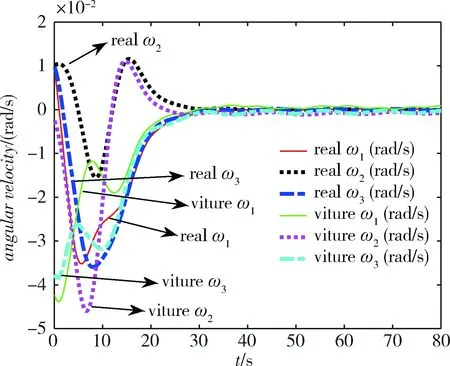
图4 MLATC控制下角速度变化曲线

图5 MLATC控制下控制力矩变化曲线
为分析文献[15]发散的原因,剔除控制饱和约束,设置控制参数
P=diag(5,5,5),Γ=diag(10,10,10),ka=diag(120,120,120),Λ=(1,1,1)Τ。
仿真时间80s,仿真结果见图6~8。图8显示,在SAAC控制器下,抓捕航天器的最大控制力矩达到130N·m,该值远远大于2.5N·m,因此,当采用饱和函数限制最大控制输入力矩为2.5N·m时,控制力矩满足不了保证航天器稳定的最小力矩,导致闭环系统最终出现发散现象。同时,图6显示,在SAAC控制下,虽然航天器姿态角也能收敛到期望姿态,但是姿态跟踪稳态误差超过0.3°,MLATC比SAAC的姿态跟踪精度高93.3%,且姿态调整过程中,姿态角存在多次振荡。航天器的角速度变化轨迹存在多次振荡,最大角速度也达到了0.4rad/s,该角速度变化范围较MLATC高近10倍,也说明了MLATC控制器使航天器拥有更高的飞行品质。
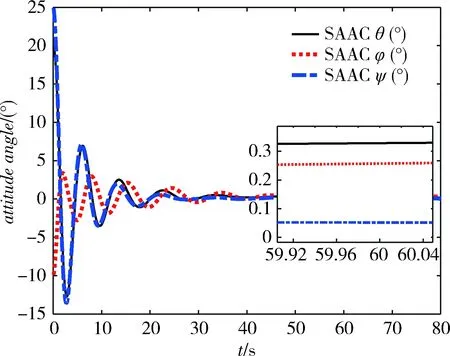
图6 SAAC控制下姿态角跟踪曲线
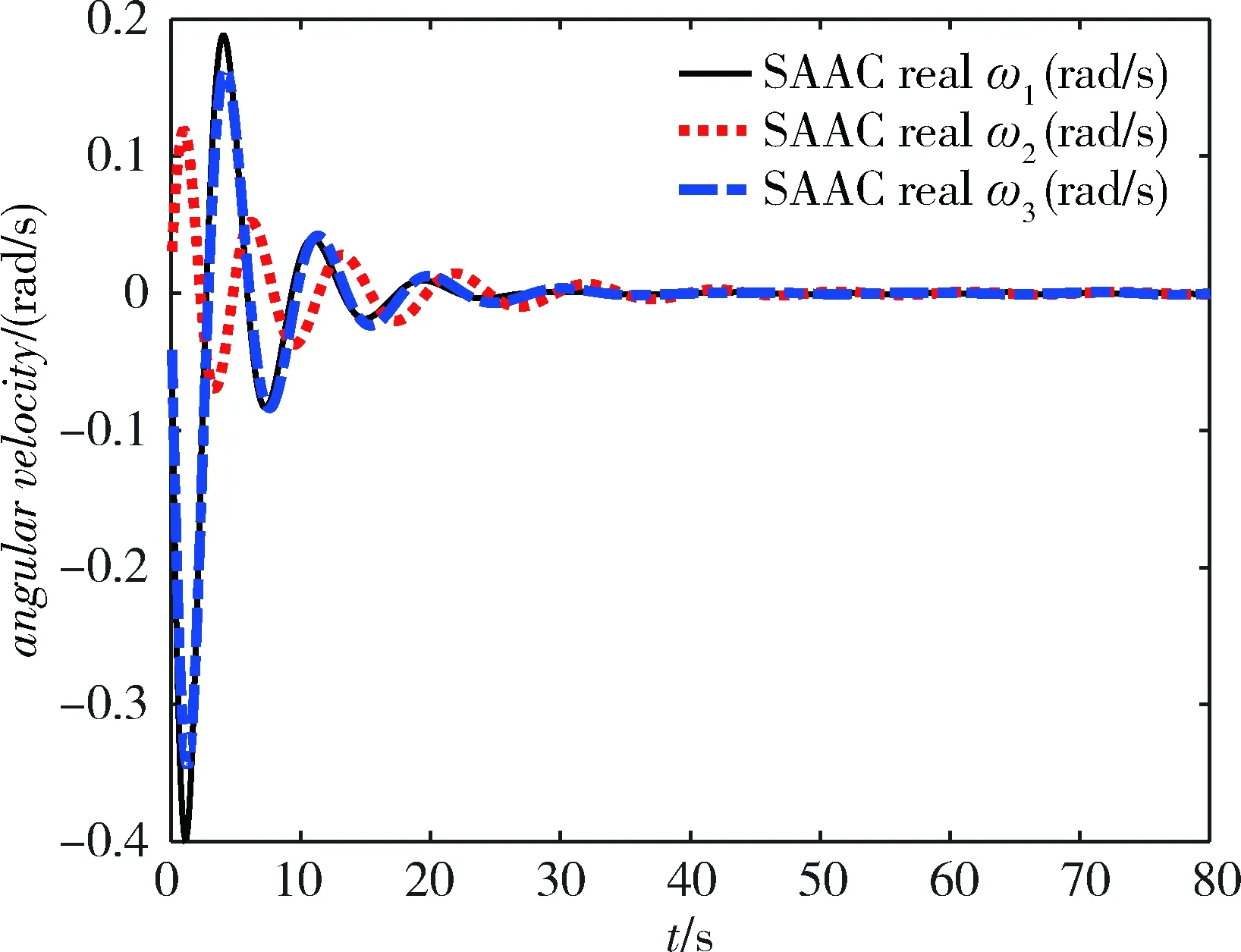
图7 SAAC控制下角速度变化曲线

图8 SAAC控制下控制力矩变化曲线
4 结论
为降低存在控制饱和约束的抓捕航天器,在抓捕非合作目标过程中的姿态跟踪稳态误差,有效提升抓捕航天器捕获非合作目标过程中的姿态跟踪精度,本文提出一种变结构姿态跟踪控制策略:
1)将姿态跟踪误差的积分项引入到姿态跟踪动力学系统中,改变姿态跟踪系统的结构,设计了多环递归跟踪姿态控制器,以提升姿态跟踪精度;
2)根据原姿态跟踪系统的控制目标,探讨了扩展后姿态动力学系统控制目标的设计方法,并给出了扩展系统的跟踪控制目标;
3)对传统反演控制方法进行改进,提出多环递归跟踪控制策略,从控制器结构上简化了反演控制器,降低了控制器的计算量。理论和仿真验证了多环递归跟踪控制策略的合理性与可行性;
4)在姿态跟踪控制器设计中考虑控制饱和约束,通过引入辅助动力学方程消除控制饱和约束,简化控制器设计。基于线性回归算子分离出未知转动惯量元素,并设计自适应更新律估计未知转动惯量,增强了航天器的鲁棒性。
[1] Yang C D, Sun Y P. Mixed H 2/H∞ State-feedback Design for Microsatellite Attitude Control[J]. Control Engineering Practice, 2002, 10(9): 951-970.
[2] Li S, Yang J, Chen W H, et al. Generalized Extended State Observer Based Control for Systems With Mismatched Uncertainties[J]. IEEE Transactions on Industrial Electronics, 2012, 59(12):4792-4802.
[3] Han J. From PID to Active Disturbance Rejection Control[J]. Industrial Electronics, IEEE Transactions on, 2009, 56(3): 900-906.
[4] Park Y. Robust and Optimal Attitude Control of Spacecraft with Inertia Uncertainties Using Minimal Kinematic parameters[J]. Aerospace Science & Technology, 2016, 54:276-285.
[5] 殷春武,侯明善,褚渊博,等.物理约束下的反演自适应姿态控制[J]. 西北工业大学学报, 2016, 34(2):281-286.(Yin Chunwu,Hou Mingshan,Chu Yuanbo,Yu Ying. Backstepping Adaptive Attitude Control with Physical Constraints[J],Journal of Northwestern Polytechnical University, 2016 (02): 281-286.)
[6] Yao Z. Attitude Tracking Control for Spacecraft with Robust Adaptive RBFNN Augmenting Sliding Mode Control[J]. Aerospace Science & Technology, 2016, 56:197-204.
[7] Leeghim H, Choi Y, Bang H. Adaptive Attitude Control of Spacecraft Using Neural Networks[J]. Acta Astronautica, 2009, 64(7): 778-786.
[8] Jiang B, Hu Q, Friswell M I. Fixed-Time Attitude Control for Rigid Spacecraft With Actuator Saturation and Faults[J]. IEEE Transactions on Control Systems Technology, 2016, 24(5):1-7.
[9] Zou A M, Ruiter A H J D, Kumar K D. Finite-time Output Feedback Attitude Control for Rigid Spacecraft Under Control Input Saturation[J]. Journal of the Franklin Institute, 2016, 353(17):4442-4470.
[10] Li B, Hu Q, Ma G. Extended State Observer Based Robust Attitude Control of Spacecraft with Input Saturation[J]. Aerospace Science & Technology, 2016, 50:173-182.
[11] Guo Y, Song S M, Li X H, et al. Terminal Sliding Mode Control for Attitude Tracking of Spacecraft under Input Saturation[J]. Journal of Aerospace Engineering, 2016, 30(3): 16-32.
[12] Gao J, Cai Y. Adaptive Finite-Time Control for Attitude Tracking of Rigid Spacecraft[J]. Journal of Aerospace Engineering, 2016, 29(4):04016016.
[13] Chen B S, Wu C S,Jan Y W. Adaptive Fuzzy Mixed H2/H∞Attitude Control of Spacecraft[J], IEEE Transactions on Aerospace and Electronic Systems, 2000,36(4) :1343-1359.
[14] Tao G. A Simple Alternative to the Barbalat Lemma [J]. IEEE Transactions on Automatic Control, 1997, 42(5):698.
[15] Yeh F K. Sliding-mode Adaptive Attitude Controller Design for Spacecrafts with Thrusters[J]. Control Theory & Applications, IET, 2010, 4(7): 1254-1264.

