拟凸变分不等式与拟凸优化问题的关系
徐智会,陈瑞婷
(重庆师范大学 数学科学学院,重庆 401331)
变分不等式是数学规划的一个重要研究领域,在工程、经济和科技等众多领域具有重要的应用. 20世纪90年代以来,该领域研究引起学者的广泛关注,其理论、算法和应用研究均取得了丰硕成果[1-5]. 在最优化理论中,凸性假设被广泛使用,为了更好地解决现实问题,一些学者对凸函数做了一系列推广. 1965年,Mangasarian[6]引进拟凸和伪凸函数的概念并研究其性质. 随后,很多学者研究了拟凸函数性质及最优性条件[7-10],由此可见拟凸函数在理论研究中的重要性. 变分不等式是解决优化问题的一个有效工具. 近年来,一些学者在研究向量优化问题时发现优化问题的最优性条件可以通过变分不等式进行刻画[11-13]. 其中,Yang和Zheng[12]研究了一个点是变分不等式近似解的充分必要条件. Lee[13]研究了几种向量变分不等式问题和非光滑向量最优问题之间的关系. 特别地,近年来,针对拟凸数值优化问题研究较多[14-16],但利用次微分给出变分不等式问题的解相对较少. 因此本文在文献[8]的基础上研究拟凸变分不等式的解与拟凸优化问题最优解之间的联系.
1 预备知识
设X为赋范向量空间,S⊂X为凸集,f:SR.
定义1[10]若f(x)在S上满足
∀x1,x2∈S,∀λ∈[0,1],f(λx1+(1-λ)x2)λf(x1)+(1-λ)f(x2).
则称f为S上的凸函数.
定义2[10]若f(x)在S上满足
∀x1,x2∈S,∀λ∈[0,1],f(λx1+(1-λ)x2)max{f(x1),f(x2)}.
则称f为S上的拟凸函数.
本文考虑如下拟凸优化问题
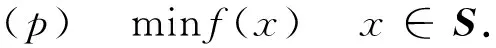
其中,可行集S⊂X为闭凸集,f是S上的拟凸函数. 设x0∈S,下面给出目标函数f的水平集和次微分的概念.
f在x0的下水平集为
[ff(x0)]:={x∈S:f(x)f(x0)}.
严格下水平集为
[f 定义3[17]设f:XR,x0∈X,若对任意的d∈X,极限 定义4[17]当f为凸函数时,次微分定义为 定义5[18]拟凸函数f:SR,在x0处的Greenberg-Pierskalla次微分定义为 星型次微分定义为 Gutiérrez次微分定义为 Plastria下次微分定义为 由定义可知 并且当f在[ff(x0)]上上半连续时,有∂⊗f(x0)=∂*f(x0)∪{0} (见文献[10]). 定义6[18]集合S在x0处的法锥定义为 定义7设x0∈S,f:XR,若f(x0) 定义8设δ>0,x0∈S,f:SR,若存在x0的一个邻域内U(x0,δ),使得x0为f在U(x0,δ)上的最优解,则称x0为f在X上的局部最优解. 定义9设X⊂Rn为给定非空闭集合,F:XRn为给定向量函数. 变分不等式记为VI(X,F),是指:求x∈X使 F(x)Τ(y-x)≥0,∀y∈X. (1) 称集合X⊂Rn为变分不等式的约束集. 引理1[19]设A,B是X中的非空凸子集,intA≠∅,若intA∩B=∅,则存在超平面分离intA和B. 考虑变分不等式定义,直观而言,式(1)意味着向量F(x)⊂Rn与始自于点x∈X的所有X可行方向成锐角,结合法锥的定义,则变分不等式VI(X,F)等价于求x∈X使-F(x)⊂NX(x),即0∈F(x)+NX(x),也就是寻找拟凸变分不等式问题的解. 本文考虑如下变分不等式问题: (VIP1)寻找x0∈S,使得存在ξ∈∂*f(x0)满足 〈ξ,x-x0〉≥0,∀x∈S. (VIP2)寻找x0∈S,使得存在ξ∈∂⊗f(x0)满足 〈ξ,x-x0〉>0,∀x∈S. 若 (VIP1) 中次微分换为∂ 定理1若x0是 (VIP1) 的解,则x0为问题(p)的最优解. 证因为x0是(VIP1)的解,则存在ξ∈∂*f(x0),对任意的x∈S,有〈ξ,x-x0〉≥0,这表明ξ∈-N(S,x0). 又有ξ∈∂*f(x0),故 ∂*f(x0)∩(-N(S,x0))≠∅. (2) 下证x0为问题(p)的最优解. 反证,设x0不是问题(p)的最优解,则存在x∈S,使得 f(x) 故由ξ∈∂*f(x0)有 〈ξ,x-x0〉<0. 又因为ξ∈-N(S,x0)故有 〈ξ,x-x0〉≥0. 从而有∂*f(x0)∩(-N(S,x0))=∅,与式(2)矛盾. 因此x0为问题(p)上的最优解. 定理2设x0∈S,f在[f(x) 证因为x0是(VIP2)的解,则存在ξ∈∂⊗f(x0),对任意的x∈S,有〈ξ,x-x0〉>0.即ξ∈-N(S,x0){0},故 ξ∈∂⊗f(x0)∩(-N(S,x0)). 即∂⊗f(x0)∩(-N(S,x0){0})≠{0}.又因为f在[f(x) ∂⊗f(x0)=∂*f(x0)∪{0}. 则 ∂*f(x0)∩(-N(S,x0))≠∅. 由定理1证明可得,x0为问题(p)上的最优解. 推论1若x0是(VIP3)的解,则x0为问题(p)上的最优解. 证因为x0是(VIP3)的解,则存在ξ∈∂ 推论2若x0是(VIP4)的解,则x0为问题(p)上的最优解. 注1定理1和2及推论1和2的逆命题不一定成立,见如下例子. 例1f:RR定义为 取S=[0,1],x0=1时,显然x0=1是问题(p)的最优解∂*f(x0)=(0,+),∀ξ∈∂*f(x0),〈ξ,x-1〉≥0,∀x∈S不成立,故定理1逆命题不成立; ∂⊗f(x0)=[0,+),∀ξ∈∂⊗f(x0),〈ξ,x-1〉>0,∀x∈S不成立,故定理2逆命题不成立; ∂ 推论3设x0∈S,f在[ff(x0)]上是上半连续的,f在x0处可微且〈f′(x0),x-x0〉>0,∀x∈S,则x0为问题(p)的最优解. 证在上述条件下有f′(x0)∈∂⊗f(x0).则由定理2可得x0为问题(p)的最优解. 定理3设x0是问题(p)的最优解,但x0不是f在全空间X上的局部最优解. 若f在[f 证令G=[f 〈ξ,μ-x0〉r〈ξ,ω-x0〉,∀ω∈S,∀μ∈G. (3) 在式(3)右端取ω=x0,〈ξ,μ-x0〉r0,∀μ∈G,这表明ξ∈∂*f(x0). 另一方面,x0不是全空间X上的局部最优解,则存在{μn}⊂G,使得μn→x0. 由式(3)左边可知〈ξ,μn-x0〉r,∀n∈N,再由μn→x0可知r≥0,所以r=0. 从而式(3)右端退化为〈ξ,ω-x0〉≥0,∀ω∈S,故x0是(VIP1)的解. 定理4令f是射线上连续的拟凸函数,f在X上的局部最优解是全局最优解,令inff(S)>inff(x),且f在[finff(S)]上是Lipschitz连续的,若x0∈S,则下列条件等价: (1)x0是问题(p)上的最优解. (2)x0是(VIP4)的解. (3)x0是(VIP3)的解. 证(1)⟹(3) 因为x0是问题(p)上的最优解,则存在ζ∈∂*f(x0),使得 〈ζ,x-x0〉≥0,∀x∈S. 又因为∂*f(x0)=R+∂ 〈λξ,x-x0〉≥0,∀x∈S. 即〈ξ,x-x0〉≥0,∀x∈S,故x0是(VIP3)的解. (2)⟹(3)由次微分定义有∂f(x0)⊆∂ (3)⟹(2)只需证∂ 〈ξ,x-x0〉f(x)-f(x0),∀x∈[f(x) 当x∈[ff(x0)],只需证f(x)=f(x0). 因为x0不是f在X上的全局最优解,由条件可知x0不是f在X上的局部最优解. 取xn→x,使得f(xn) 〈ξ,xn-x0〉f(xn)-f(x0). 因为f在[finff(S)]上是上半连续的,有 〈ξ,x-x0〉f(x)-f(x0),∀x∈[f(x)f(x0)].所以ξ∈∂f(x0),得证. 由推论1,(3)⟹(1)成立. 定理5对任意凸集C⊂S,S0是f在问题(p)上的最优解集且S0∩C≠∅,若存在ξ∈∂f(x0),对任意的x∈S0∩C,y∈C,有〈ξ,y-x〉≥0,则ξ是不变的. 如果f上半连续且满足inff(S)>inff(x),对任意的ξ∈∂ 证取x0,x1∈S0∩C,由条件知∀ξ∈∂f(x0).且〈ξ,y-x〉≥0,∀y∈C,有〈ξ,x1-x0〉≥0,由∂f(x0)定义, 〈ξ,x-x0〉f(x)-f(x0),∀x∈[f(x)f(x0)]. 有〈ξ,x1-x0〉f(x1)-f(x0)=0,故〈ξ,x1-x0〉=0. 从而有 〈-ξ,y-x1〉=〈-ξ,y-x0〉0,∀y∈C. 这说明〈ξ,y-x1〉≥0,∀y∈C.下证ξ∈∂f(x1). 因为y∈[ff(x1)]=[ff(x0)],所以 〈ξ,y-x1〉=〈-ξ,y-x0〉f(y)-f(x0)=f(y)-f(x1). 故ξ∈∂f(x1). 得证. 若f上半连续的,由定理4证明有∂f(x1)=∂ 下面举例说明定理5中的ξ是不变的. 例2f:RR定义为 令S=[0,3],C=[0,2],S0=[0,1],满足定理中的条件,取x0=0,∂f(0)=0,满足〈0,y-x0〉≥0,即ξ=0. 取x1=1时,∂f(1)=[0.+),要满足〈ξ,y-x1〉≥0,则ξ=0. 本文关注到变分不等式的最优解与数值优化问题的最优解有密切联系,于是利用拟凸变分不等式给出了拟凸优化问题最优解的刻画,并研究两者最优解的必要和充分条件,并通过实例说明其合理性. 不足的是,仅针对拟凸数值优化问题研究,因此在本文基础上,还可以将拟凸数值优化问题推广到多目标拟凸优化问题,利用变分不等式研究解、近似解的充分必要条件. 参考文献: [1] Facchinei F,Pang J S. Finite-dimensional variational inequalities and complementarity problems[M]. NewYork:Springer,2003. [2] Yang X Q. Vector variational inequality and vector pseudolinear optimization[J]. Journal of Optimization Theory and Applications,1997,95(3):729-734. [3] Ferris M C,Pang J S. Engineering and economic applications of complementarity problems[J]. Siam Review,1997,39(4):669-713. [4] Chen G Q,Cao B. A new NCP-function for box constrained variational inequalities and a related Newton-type method [J]. Mathematica Numerica Sinica,2002(1):91-104. [5] Bernstein D. Avariational inequality approach,by Anna Nagurney[J]. Advancesin Computational Economics,1993,1. [6] O L Mangasarian. Pseudo Functions[J]. Journal of the Society for Industrial and Applied Mathematics,1965,3(2):23-32. [7] J P Penot. What is quasiconvex analysis?[J]. Optimization,2000,47(1-2):35-110. [8] J P Penot. Characterization of Solution Sets of Quasiconvex Programs[J]. Journal of Optimization Theory and Applications,2003,117(3):627-636. [9] T H L Nguyen,J P Penot. Optimality Conditions for Quasiconvex Programs[J]. Siam Journal on Optimization,2006,17(2):500-510. [10] 杨新民,戎卫东. 广义凸性及其应用[M]. 北京:科学出版社,2016. [11] Yang X Q,Goh C J. On vector variational inequalities: Application to Vector Equilibria[J]. Journal of Optimization Theory and Applications,1997,95(2):431-443. [12] Yang X Q. Zheng X Y. Approximate solutions and optimality conditions of vector variational inequalities in Bamach spaces[J]. J. Glob. Optim,2008,40:455-462. [13] Lee G M,Lee K B. Vector varational inequalities for nondifferentiable convex vextor optimization problems[J]. Journal of Global Optimization,2005,32(4):597-612. [14] 孙菊贺. 锥约束变分不等式问题的数值方法的研究[D]. 大连:大连理工大学,2008. [15]曾云辉. 变分不等式的数值解法研究[D]. 西北大学,1999. [16] 胡淑娟,王希营,丁方允. 关于变分不等式问题近似解的数值证明[J]. 计算力学学报,2006,23(1):40-45. [17] 胡毓达,孟志青. 凸分析与非光滑分析[M]. 上海:上海科学技术出版社,2000. [18] Demyanov V F. Nonsmooth Optimization[M]. NewYork:World Scientific,1992. [19] Yoshikazu Sawaragi,Hirotaka Nakayama,Tetsuzo Tanino. Theory of multiobjective optimization[M]. Orlando:Academic Press,1985.
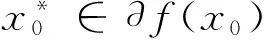
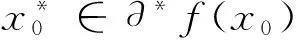
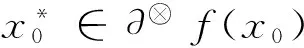
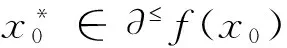
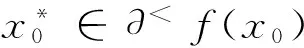
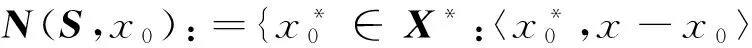
2 拟凸变分不等式与拟凸优化问题的关系
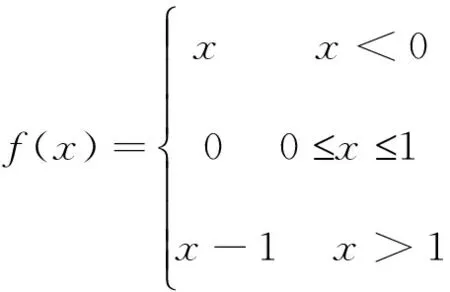

3 结论

