五阶KdV方程解正则性的传播*

石宁玄

(华北电力大学数理学院，北京 102206)

Kawahara方程[1]是非线性色散方程的一种,其形式为

(1)

其中x,t∈R.当α=0,β=-1时,方程(1)即为五阶KdV方程，其形式为

(2)

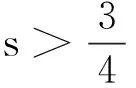
1 预备知识

先引入截断函数[3]

显然有

引理1[2]对于∀u0∈Hs(R)，IVP的唯一解满足：

(ⅰ)u∈C([-T,T]:Hs)；

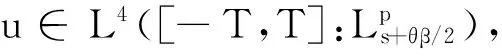
(ⅲ)∂xu∈L4([-T,T]:L∞).

2 主要结果及其证明

定理1如果u0∈H3/4+(R)，存在l∈Z+，l≥1且x0∈R，使得

(3)

同时方程(2)的解满足引理1，那么：

(ⅰ)对于∀v>0，ε>0，有

(4)

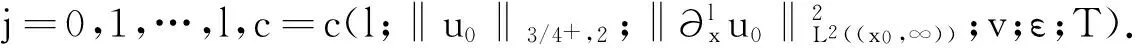
(ⅱ)对于∀v≥0，ε>0，R>0，有

(5)

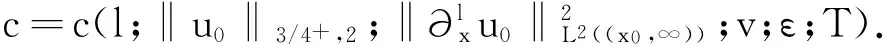
证明以(4)和(5)式中l=1为例说明研究正则性推广的方法.

当l=1时.先对方程(2)两边关于x求偏导，然后同时乘以∂xuχ0,ε,b(x+vt)，最后对等式两边的x进行积分，可得

(6)

其中v∈R，v≥0.此后的证明中将省略χ0,ε,b中的固定值ε,b.在[0,T]上对时间进行积分后整理(6)式可得

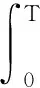
(7)

分析(7)式的各个部分，并由引理1(ⅲ)，可得

c1(v;T;ε;b)≤c0(v;T;ε;b) .

(8)

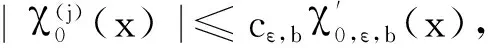
(9)

(10)

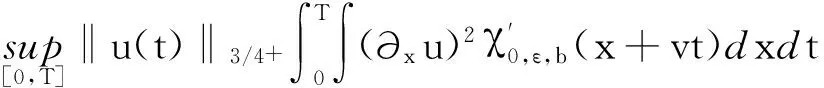
(根据Sobolev嵌入[5])≤c0.

(11)

综合(7)—(11)式，进行整理，可得

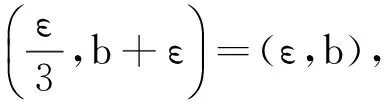
其中c0=c0(ε;b;v)>0，对于∀ε>0，b≥5ε，v>0.

当l≥2时.假设u0满足(3)式i.e.，

(12)

其中j,k=1,2,…,l,l≥2，对于∀ε>0,b≥5ε,v>0.由(12)式可知，u0|(0,∞)∈Hl+3([0,∞)).同理，对∀ε>0，b≥5ε，可得

(13)

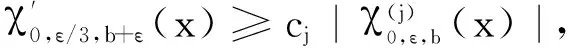
因A3(t)比较复杂，故对其进行分步考虑.令l+1=3，可得：

为了方便接下来的证明，在suppχ0,ε,b⊆[ε,∞)上建立一个截断函数，χ0,ε/5,ε(x)=1，则有

当l≥3时.分析(13)式，可得：

(14)

观察(14)式可发现，对于3≤j≤l-1，

c0(将j,j+1代入(12)式即得).

定理1证毕.

解的衰减性质的证明与定理1的证明类似，也可参考文献[4].文献[4]中的定理1体现了三阶KdV方程解的正则性与衰减性的延拓，而本研究结果体现了五阶KdV方程解的正则性的延拓.

[1] KAWAHARA T.Oscillatory Solitary Waves in Dispersive Media[J].Journal of the Physical Society of Japan,1972,33(1):260-264.

[2] KENIG CARLOS E,PONCE GUSTAVO,VEGA LUIS.A Bilinear Estimate with Applications to the KdV Equation[J].Journal of the American Mathematical Society,1996,9(2):573-603.

[3] EVANS LAWRENCE C.Partial Differential Equations[M].2 Edition.Providence,Rhode Island:American Mathematical Society,1997:254-284;649-688.

[4] ISAZA PEDRO,LINARES FELIPE,PONCE GUSTAVO.On the Propagation of Regularity and Decay of Solutions to thek-Generalized Korteweg-de Vries Equation[J].Communications in Partial Differential Equations,2015,40(7):1 336-1 364.

[5] 张恭庆.泛函分析讲义[M].北京:北京大学出版社,2008:22-27.