并联电抗器铁心振动的模型实验与仿真研究

田 聪， 李 琳， 宋雅吾， 张鹏宁， 王晓燕， 程志光， 刘兰荣,聂京凯， 樊 超(. 新能源电力系统国家重点实验室， 华北电力大学， 北京 006； . 国家硅钢工程技术研究中心， 湖北 武汉 0080； . 保定天威保变电气股份有限公司， 河北 保定 07056;. 国家电网全球能源互联网研究院， 北京 009)

1 引言

并联电抗器对于保持电力系统无功平衡，提高电力系统稳定性[1,2]有重要作用。但由于并联电抗器铁心的多气隙结构和强漏磁场的工作特点，在其运行过程中振动和噪声问题非常突出，这不仅产生噪声污染，同时也会对并联电抗器的安全稳定运行产生不利影响，因而并联电抗器的振动噪声问题引起了国内外学者的广泛关注。文献[3]指出并联电抗器振动噪声的来源主要有：①铁心漏磁作用在绕组上产生的洛伦兹力引起的绕组振动；②作用于铁心表面的麦克斯韦力引起的铁心振动和铁心磁致伸缩效应产生的振动。由于正常工况下并联电抗器绕组所受洛伦兹力远小于麦克斯韦力和等效磁致伸缩力，因而在并联电抗器振动分析中一般忽略其影响，主要考察麦克斯韦力和磁致伸缩效应导致的并联电抗器铁心振动。

国内外学者对电力设备振动问题进行了大量研究。Peng Shuai基于麦克斯韦力和绕组洛伦兹力考察了中频中压变压器的振动问题[4]。Gao Yanhui等在考虑电磁力和磁致伸缩效应的基础上对并联电抗器的磁场和振动场分布做了深入研究[5-7]，其具体做法如下：首先通过数值计算方法计算空间磁场分布，然后利用该磁场解来求解并联电抗器铁心所受电磁力；同时按照文献[8]所给出的节点力求解方法，将磁致伸缩效应等效为磁致伸缩节点力，来进行振动求解。文献[5]比较了麦克斯韦力与磁致伸缩效应对并联电抗器振动的影响。文献[6]提出采用寻找最佳硬度的绝缘材料来填充铁心气隙以降低并联电抗器振动的方法。文献[7]采用一种近似的均匀化方法来等效叠片铁心并进行了数值计算验证。文献[9]主要分析了各类谐波状况对电抗器所受麦克斯韦力及其振动特性的影响。文献[10]在考虑磁致伸缩效应和电磁力的基础上对可控饱和并联电抗器振动进行了仿真分析，具有一定的参考意义。

文献[4-10]对电抗器振动的研究集中在额定负载情况下的振动特性，并未涉及对轻载情况下电抗器的振动分析，同时也未指出不同工况下电抗器振动分析的差异。本文在考虑不同负载对电抗器振动影响的基础上，设计制作了一台并联电抗器试验模型，并应用有限元软件对并联电抗器模型的磁场进行了计算，分别在仅考虑麦克斯韦力和同时考虑麦克斯韦力及磁致伸缩效应的情况下，对不同工况下的并联电抗器振动进行了仿真分析，并将计算结果同实验结果进行了比较。

2 电磁与振动特性分析方法

2.1 磁场方程

并联电抗器正常运行时，由绕组电流激励在铁心中产生交变磁场。该时谐场所满足的方程为：

(2)

式中，H为磁场强度；E为电场强度；B为磁感应强度；J为电流密度；t为时间。引入矢量磁位A，可得到：

(3)

式中，ν为磁阻率。而电流密度J可表示为：

(4)

式中，N为线圈匝数；Icoil为线圈电流；S为绕组截面积；ecoil为导线方向矢量。根据式(1),式(2)和式(3)，利用三维涡流场求解的矢量磁位A方法，可得所需求解的方程为：

(5)

式中，σ为媒质的电导率；Js为外加激励电流密度。根据所施加边界条件，结合式(5)，即可求解得到所需的矢量位A以及磁通密度值B。

2.2 麦克斯韦力

在求得铁心磁通密度分布之后，按式(6)求解作用在铁心表面的麦克斯韦应力，然后对其在铁心表面按照式(7)积分得到铁心所受麦克斯韦力。计算中忽略叠片铁心的端部效应，则铁心表面麦克斯韦力的求解如下[11]：

(6)

(7)

式中，p为麦克斯韦应力；μ0为真空磁导率；n为求解表面法向单位矢量；B为求解表面磁通密度；F为求解表面麦克斯韦力；S为求解表面。式(6)和式(7)表示成麦克斯韦张量公式为：

(8)

(9)

式中，ΤMax为张量形式的麦克斯韦应力；下标x、y和z表示变量在直角坐标系中的三个分量。麦克斯韦应力的方向与磁力线的方向相同，其穿过磁媒质表面时产生拉压力，而其大小与其所穿磁媒质表面法向分量的大小有关。并联电抗器铁心表面麦克斯韦力在其气隙表面最大，因在忽略气隙边缘磁通时，气隙处磁力线几乎是垂直穿过铁心外表面。并联电抗器的铁心结构是对称的，所以麦克斯韦力在单个铁心饼气隙表面方向相反；但由于存在漏磁场，单个铁心饼上下两个气隙表面上的法向磁场不是严格相等，法向净麦克斯韦力不为零。

2.3 磁致伸缩效应

磁致伸缩效应与铁磁物质的磁化过程有关。磁性材料在外加磁场的作用下，其自身会磁化，磁化过程中其内部原本随机取向的磁畴此时取向排列，导致其长度在磁化方向上的伸长或缩短[12，13]。这种长度的改变会在材料内部产生应力，称为磁致伸缩应力。该效应是造成电力变压器和并联电抗器铁心振动的主要原因之一[14-16]。本文采用弹性力学的应力应变关系将磁致伸缩应变等效为磁致伸缩应力，然后作为体载荷进行计算分析。具体做法为：首先根据测量得到的磁致伸缩蝴蝶曲线提取出磁致伸缩峰峰值和磁通密度的对应关系，然后利用三次样条插值方法，获得磁通密度与磁致伸缩值的函数关系；将该函数关系与所求磁场结合，来求解磁致伸缩效应引起的铁心振动位移。

三维弹性体应力应变关系为[17]:

σ=Dε

(10)

式中，ε为磁致伸缩应变；σ为等效磁致伸缩应力；D为三维线弹性材料的弹性张量，其表达式为:

(11)

其中，E为材料杨氏模量；α为材料泊松比；P和Q分别为：

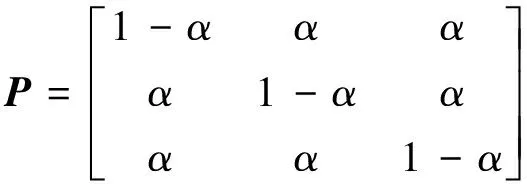
(12)

(13)

其中，I为三阶单位矩阵。

将磁致伸缩应变代入式(10)中，可以求得铁心磁致伸缩效应产生的磁致伸缩应力。

2.4 铁心振动特性分析

任意连续多自由度系统振动的微分方程为：

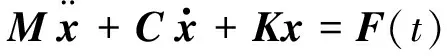
(14)

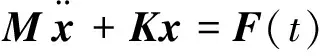
(15)

同时代入磁致伸缩力与麦克斯韦力，得：

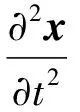
(16)

式中，F(t)em为广义电磁力，由磁致伸缩力和麦克斯韦力构成，同时根据磁致伸缩应力和麦克斯韦应力计算电磁力的公式为：

F(t)em=F(t)Max+F(t)ms

(17)

(18)

式中，F(t)Max为麦克斯韦力；F(t)ms为磁致伸缩力；σMax和σms分别为麦克斯韦应力和磁致伸缩应力。将式(18)代入式(16)可得最终求解方程：

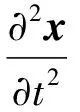
(19)

对偏微分方程式(16)采用有限元方法进行离散，得到电磁机械耦合矩阵[3，18]:

(20)

式中，M为电磁刚度矩阵；D为位移对物质磁化特性的影响矩阵；C为物质磁化过程对位移的影响矩阵；K为电磁刚度矩阵；x为位移。分析中忽略位移对物质磁化影响，因此D=0，同时调整方程得：

(21)

F(t)em=-CA

(22)

通过求解式(21)、式(22)可以得到并联电抗器铁心振动位移。将式(21)求解得到的位移x代入式(23)：

(23)

求得铁心应变ε。

3 实验与计算结果分析

3.1 并联电抗器试验模型

本文设计制作了一台单相并联电抗器试验模型，该模型如图1所示。铁心外尺寸为570mm×598mm×61mm，关于中线对称开两窗口，窗口尺寸为114.5mm×429mm，两旁柱分别宽80.5mm，两绕组串联，分绕于两旁柱之上。中心柱宽180mm，其距底轭214.5mm处开一2mm气隙以达到所需的电感值。

图1 单相并联电抗器试验模型Fig.1 Single phase shunt reactor model

3.2 实验与计算结果分析

本文以图1所示的单相并联电抗器试验模型为研究对象，通过有限元方法计算得到并联电抗器模型的磁通密度分布，然后根据该分布根据式(8)计算出作用在并联电抗器模型铁心表面的麦克斯韦应力，将该力作为并联电抗器振动的激振力施加于并联电抗器铁心表面，从而通过求解振动方程来实现并联电抗器振动场的求解。在仿真分析中同时考虑了麦克斯韦力和磁致伸缩对并联电抗器振动的影响。对模型并联电抗器在不同工作电压条件下的磁通密度分布和机械振动特性等进行了分析。仿真分析中对模型并联电抗器进行的网格剖分如图2所示。

图2 并联电抗器试验模型网格剖分图Fig.2 Mesh generation of model shunt reactor

图3 模型并联电抗器铁心H-B曲线Fig.3 Iron core H-B curve of model shunt reactor

图4 磁致伸缩随磁通密度变化曲线Fig.4 Magnetostriction-B curve

模型用硅钢片磁化特性曲线如图3所示。根据测量得到硅钢片磁致伸缩蝴蝶曲线，提取出磁致伸缩峰峰值和磁通密度的对应关系，结果如图4所示。

模型工作频率为50Hz，采用电压源激励方式。在时域求解器设置中，取时间步长为0.5ms，求解总时长为15个周期。为了准确求解气隙处磁密，气隙附近处铁心网格做了特别细化。考虑原模型的对称结构，为减少计算量，截取原模型一半进行数值分析计算。

采用改变工作电压的方法来改变并联电抗器的工况，并联电抗器在0.3s时磁通密度分布如图5所示。根据仿真结果，铁心气隙附近磁通密度随着激励电压的增大而不断增大，分别为0.43T和1.0T。而铁心最大磁密也随激励电压增大而增大，且均出现在铁心柱轭搭叠转角处，分别为1.0T和1.57T。图1中测点A处实验测得平均磁密与同一测点仿真结果对比如表1所示。可知实验与仿真结果基本符合。

图5 不同电压下并联电抗器磁通密度分布图Fig.5 Flux distribution under different voltage for shunt reactor

表1 测磁线圈与仿真磁通密度(平均值)对照表Tab.1 Contrast table for flux density of measured and simulated

表1显示，并联电抗器磁通密度仿真值与实验值误差最大值小于1%，可以认为仿真值与实验值吻合,仿真计算能够真实反映并联电抗器的电磁特性。图6给出了0.3s时铁心气隙处麦克斯韦应力z轴分量在不同工况下的值。

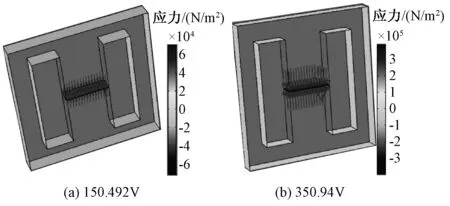
图6 不同工况下气隙麦克斯韦应力z分量分布Fig.6 Distribution of Maxwell force z component in air gap under various voltage

由图6可以看出，麦克斯韦力主要作用于磁通密度垂直穿出铁心表面处。对比不同工况下铁心所受麦克斯韦力可知，该力的大小与并联电抗器工况有关，两种工况下铁心单位面积上麦克斯韦力z分量最大值相差一个量级，分别为65kPa和330kPa。

在振动位移求解时，并联电抗器下铁轭底部设定位移为零，即固定约束，用以模拟铁心体站立时的约束状态。图7为不同控制电压下仅麦克斯韦力作用引起并联电抗器铁心振动的位移场。可以看出，并联电抗器最大位移发生在中间铁心柱气隙处，电压150V时为1.65μm，350V时为23.2μm。对比可知，铁心麦克斯力引起的并联电抗器振动位移随工作电压的增大而增大，这与分析是一致的。因为从式(8)可知，麦克斯韦力与磁通密度是正相关的。

图7 仅麦克斯韦力作用时不同控制电压下并联电抗器的铁心位移Fig.7 Displacement of iron core under various voltages when only Maxwell force excitation

图8为0.3s时，铁心在麦克斯韦力和磁致伸缩效应共同作用下产生的位移分布图。

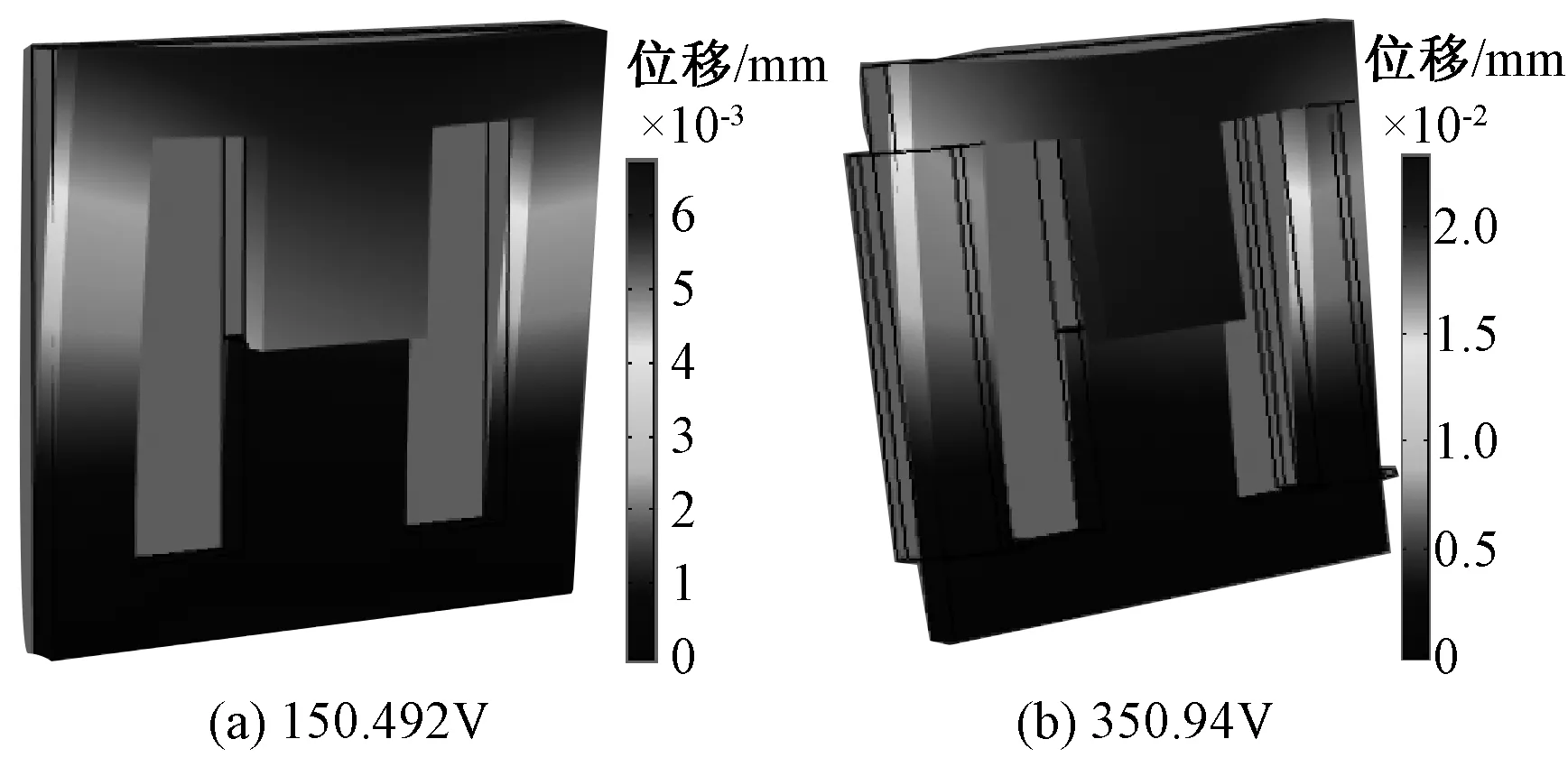
图8 考虑麦克斯韦力和磁致伸缩效应的并联电抗器位移Fig.8 Displacement of shunt reactor considering magnetostriction and Maxwell force

分析图8可知，在麦克斯韦力和磁致伸缩应力共同作用时，铁心的最大位移依然发生在铁心柱气隙处。对比图7和图8可得各类工况下是否考虑磁致伸缩时的最大位移及产生的误差，结果如表2所示。

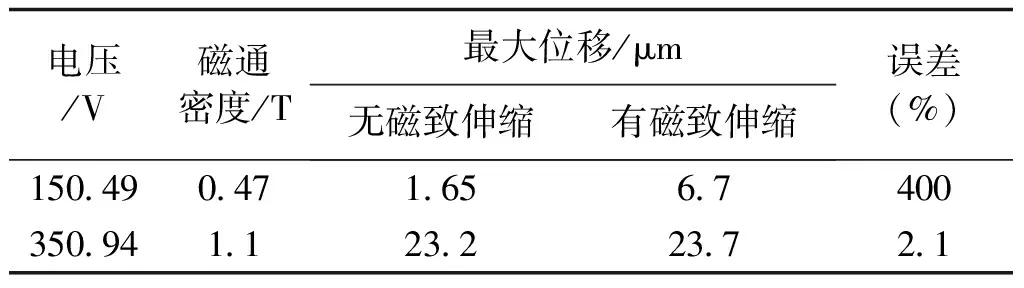
表2 各工况下是否考虑磁致伸缩时的最大位移及产生的误差Tab.2 Error when taking or not taking magnetostriction in analysis under various working conditions

由表2可以看出，并联电抗器铁心工作在0.47T的低磁密状态下时，分析其振动不考虑磁致伸缩效应将造成高达400%的误差。而当其工作在1.1T的高磁密状态下时，不考虑磁致伸缩效应在振动位移分析中产生的误差仅为约2.1%。即磁致伸缩效应在并联电抗器铁心振动位移中的贡献与其工作磁通密度有关。因此在进行并联电抗器振动位移分析时，若铁心处于磁通密度较低的轻载工况下，则在位移分析时必须考虑磁致伸缩效应的影响，否则就会产生错误；若负载较大或处于额定负载，此时铁心磁通密度接近或者处于饱和，那么分析时可以不计入铁心磁致伸缩效应对振动位移的影响，这种简化可以满足工程所需的精度要求。

图9为150V电压下并联电抗器测点A处的振动加速度实验仿真波形对比。可知，加速度的测量值和仿真计算值波形相符，而极值有一定误差。

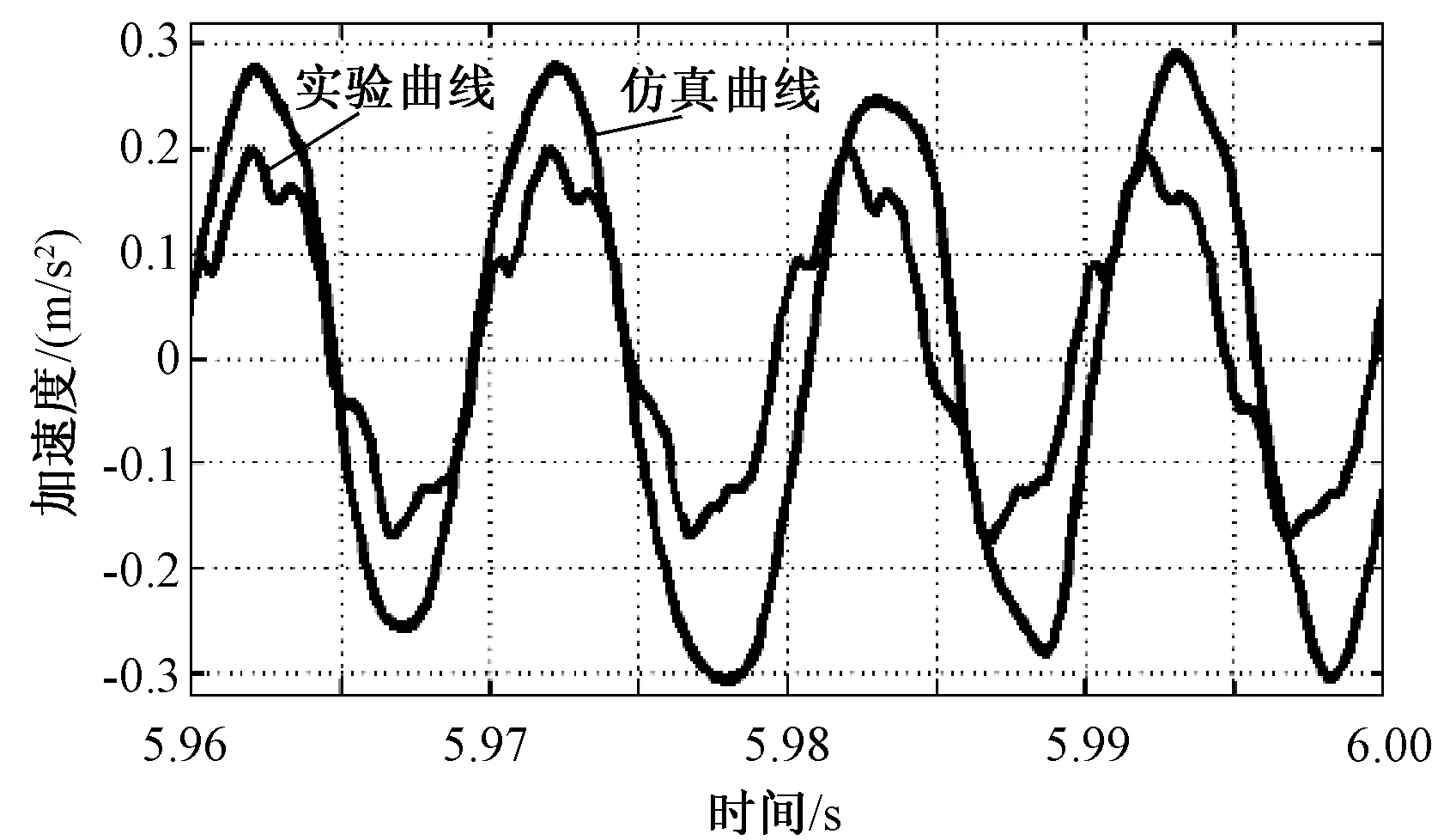
图9 150V激励时加速度实验与仿真波形对比Fig.9 Acceleration wave contrast of measured and simulation under 150V excitation

造成实验与仿真误差的原因有以下几点：

(1)实际并联电抗器底部并不是严格固定约束。

(2)实验过程中调压器波形不严格正弦。

(3)试验中实验仪器放置于木桌上，这也会影响实验的精确度。

(4)并未考虑固有频率对并联电抗器振动造成的影响。

控制上述影响因素在实验中所产生的误差是产生较好实验仿真匹配曲线的关键。

4 结论

本文围绕一台单相并联电抗器模型，对其进行了系列振动实验及三维的电磁机械耦合振动分析。测量了模型在不同工况下的磁通密度和振动加速度曲线，同时仿真研究了该模型在不同工况下的磁场分布及麦克斯韦力和磁致伸缩共同作用下的振动位移及加速度。实验和仿真结果对比表明：

(1)在轻载工况下，磁通密度较低，分析电抗器振动应同时考虑电磁力和磁致伸缩效应的影响。

(2)在额定工况下，磁通密度较高时，分析电抗器振动时，是否考虑磁致伸缩效应已不会产生较大误差。

因此可以得出结论：电磁力和磁致伸缩效应对并联电抗器振动的影响与工作磁通密度有关。磁致伸缩效应对其振动的贡献随工作磁通密度的增大逐渐减弱，到接近于额定工况时，电抗器振动分析可以仅考虑电磁力的影响而忽略磁致伸缩效应。

[1] Liu Wenye, Luo Longfu, Dong Shuda, et al. Overview of power controllable reactor technology [J]. Energy Procedia, 2012, 17: 483-491．

[2] 郑涛,赵彦杰(Zheng Tao, Zhao Yanjie). 超/特高压可控并联电抗器关键技术综述(Overview of key techniques of EHV/UHV controllable shunt reactor)[J]. 电力系统自动化(Automation of Electric Power Systems), 2014, 38(7)：127-135.

[3] Rossi M, Besnerais J. Vibration reduction of inductors under magnetostrictive and Maxwell forces excitation [J]. IEEE Transactions on Magnetics, 2015, 51(12): 1-6.

[4] Shuai P, Biela J. Investigation of acoustic noise sources in medium frequency, medium voltage transformers [A]. 2014 16th European Conference on Power Electronics and Applications[C]. Lappeenranta, Finland, 2014. 1-11.

[5] Gao Y, Muramatsu K, Fujiwara K, et al. Vibration analysis of a reactor driven by an inverter power supply considering electromagnetism and magnetostriction[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4789-4792.

[6] Gao Y, Muramatsu K, Hatim M, et al. Design of a reactor driven by inverter power supply to reduce the noise considering electromagnetism and magnetostriction[J]. IEEE Transactions on Magnetics, 2010, 46(6): 2179-2182.

[7] Gao Y, Muramatsu K, Hatim M, et al. The effect of laminated structure on coupled magnetic field and mechanical analyses of iron core and its homogenization technique[J]. IEEE Transactions on Magnetics, 2011, 47(5): 1358-1361.

[8] Kameari A. Local force calculation in 3D FEM with edge elements[J]. International Journal of Applied Electromagnetics in Materials, 1993, 3: 231-240.

[9] Yan Rongge, Gao Xu, Zhu Lihua, et al. Research on three-dimensional stress distribution of reactor core[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4):1-4.

[10] 杨意妹,祝丽花,王斌,等(Yang Yimei, Zhu Lihua, Wang Bin, et al.).考虑磁致伸缩效应的可控饱和并联电抗器电磁振动分析(Analysis on electromagnetic vibration of controllable saturable reactor considering magnetostrictive effects)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2016, 35(8): 40-45.

[11] 颜威利,杨庆新,汪友华(Yan Weili, Yang Qingxin, Wang Youhua).电气工程电磁场数值分析(Numerical analysis of electrical engineering electromagnetic field)[M]. 北京:机械工业出版社(Beijing: China Machine Press), 2005.

[12] 郭贻诚(Guo Yicheng). 铁磁学(Ferromagnetics)[M]. 北京:北京大学出版社(Beijing: Peking University Press), 2014.

[13] 张艳丽，王佳音，白保东,等(Zhang Yanli, Wang Jiayin, Bai Baodong, et al.). 直流偏磁磁场对硅钢片磁致伸缩特性的影响分析(Influence analysis of DC biased magnetic field on magnetostrictive characteristics of silicon steel sheet)[J].中国电机工程学报(Proceedings of the CSEE)，2016，36(15)：4299-4307.

[14] Jang P, Choi G. Acoustic noise characteristics and magnetostriction of Fe-Si powder cores[J]. IEEE Transactions on Magnetics, 2012, 48(4): 1549-1552.

[15] Belahcen A, Singh D, Rasilo D, et al. Anisotrpopic and strain-dependent model of magnetostriction in electrical steel sheets[J]. IEEE Transactions on Magnetics, 2015, 51(3): 1-4.

[16] Li Q, Wang X, Zhang L, et al. Modelling methodology for transformer core vibrations based on the magnetostrictive properties[J]. IET Electric Power Applications, 2012, 6(9): 604-610.

[17] Ebrahimi H, Gao Y A. Kameari A, et al. Coupled magneto-mechanical analysis considering permeability variation by stress due to both magnetostriction and electromagnetism[J]. IEEE Transactions on Magnetics, 2013, 49(5): 1621-1624.

[18] 祝丽花, 杨庆新, 闫荣格, 等(Zhu Lihua, Yang Qingxin, Yan Rongge, et al.). 电力变压器铁心磁致伸缩力的数值计算(Numerical calculation of magnetostrictive stress of core in power transformer)[J]. 变压器(Transformer), 2012, (6):9-13.