RoboCup3D仿真机器人步态优化研究

何荣义,李春光

(1.河海大学计算机与信息学院,江苏 南京 210098; 2.常州工学院计算机信息工程学院,江苏 常州 213002)

0 引 言

RoboCup机器人世界杯每年举办一次，吸引了众多学者参与。RoboCup活动促进了人工智能、多智能体系统以及机器人技术等领域的发展。在双足机器人足球竞赛中，机器人能否在复杂动态的环境中灵活快速、稳定地行走对比赛结果起着重要的影响。

双足步态模式生成一般分为2类。一类运用简化动态模型，通过反馈控制实现双足机器人的步态行走,另一类通过精确的动态模型生成稳定步态。这2类模型都有各自的优缺点，本文将选择第一类简化模型。不同的步态模型会产生不同的步态效果，Graf等人[1]提出一种闭环的三维线性倒立摆模型(3D-LIPM)，通过零力矩点(ZMP)生成质心轨迹，虽然该模型可实现双足机器人任意方向的行走，但由于它是线性的，在行走过程中质心高度是固定不变的。然而生物力学研究表明：人类在行走过程中，质心高度是变化的[2]。Guo等人[3]在此基础上提出垂直质心高度补偿方法，但该步态方法很容易引起震荡[4]。

双足机器人拥有众多自由度，有着复杂的非线性系统，机器人在行走过程中很难控制它的平衡。Macalpine等人[5]以双线性倒立摆为模型，运用自适应协方差矩阵进化算法(Covariance Matrix Adaption Evolution Strategy,CMA-ES)[6]对步态参数进行分层优化，实现了双足机器人的全向运动。Shafii等人[7]通过修正傅里叶级数生成角轨迹，利用粒子群算法(Particle Swarm Optimization,PSO)优化傅里叶级数参数，优化出快速稳定的直线行走。Hong等人[4]通过中枢模式发生器(Central Pattern Generator,CPG)补偿步态震荡，将它看作约束优化问题，通过进化算法优化，实现了双足机器人质心高度可变的大步行走。

根据以上分析，本文通过规划双足机器人Z轴方向的质心以及零力矩点(Zero-Moment Point,ZMP)的轨迹，以倒立摆[8]为基本模型，利用离散化[9]方法生成水平质心轨迹。根据之前手动调试经验，从步态模式中提取影响步态速度和稳定的关键参数，对所设定的目标函数利用CMA-ES算法进行分层优化[10]，实验结果表明了该方法的有效性。

1 步态设计模式

1.1 倒立摆模型

ZMP是判定双足机器人步态稳定的重要指标，虽然ZMP无法直接生成步态轨迹，但它可以判定生成的步态轨迹是否能保持双足机器人的平衡。机器人行走过程中，当ZMP始终在支撑多边形框内时，双足机器人才能保持稳定。双足行走轨迹可以通过给定ZMP的目标轨迹，计算可行的质心轨迹得到。质心轨迹可以通过简化的物理模型来近似，如三维线性倒立摆模型、倒立摆模型[8]等。

倒立摆模型是由Kajita等人[8]提出，他将双足机器人简化为一个质点以及一个可伸缩无质量的连杆。与三维线性倒立摆模型中垂直质心高度是固定值相比，倒立摆模型中的垂直质心高度是可变的。设质心的位置为c=(cx,cy,cz)，ZMP的位置为p=(px,py,0)。为了简化双足规划，本文只考虑X,Y轴方向的运动轨迹，其方程式为：

(1)

(2)

本文通过给定垂直质心高度和ZMP轨迹求出水平质心的轨迹。同时，为了解决双足机器人支撑腿切换过程中与地面的碰撞问题，本文采用简谐运动合成的方法来规划摆动腿轨迹。

1.2 垂直质心高度和ZMP轨迹生成

垂直质心高度可以显著提高双足步行速度[4,7,11]。有许多方法可以生成垂直质心高度轨迹，如优化中枢模式发生器[4]、傅里叶级数等[7,11]。本文将选择四次多项式为垂直质心轨迹，如式(3)所示：

x(t)=a0+a1t+a2t2+a3t3+a4t4

(3)

其中,a0,a1,a2,a3,a4是需要优化的参数。

文献[12]研究表明：双足机器人在拥有移动的ZMP轨迹时行走更加高效，为了获得这样的轨迹，在单腿支撑阶段本文将采用直线方程表示ZMP轨迹。设支撑脚的中心为坐标原点，方程可表示为：

(4)

其中,pxmin,pxmax分别为脚跟和脚趾的位置，Ts为周期，侧向ZMP为支撑脚的中心。

1.3 水平质心轨迹生成

式(3)和式(4)已经给出了垂直质心以及ZMP轨迹，根据式(1)和式(2)求解微分方程可以算出水平质心的轨迹。Kagami等人[9]提出一种快速有效地求解微分方程的方法，将ZMP方程用采样时间Δt离散化来近似加速度：

iΔt→i, cx(iΔt)→cx(i)

(5)

(6)

其中,i=1,…,n。离散化后的ZMP方程为：

px(i)=αicx(i-1)+βicx(i)+αicx(i+1)

(7)

(8)

(9)

将公式(7)写成矩阵的形式，则有：

(10)

共有Ns=Ts/Δt行。文献[9]提出一种解决边界问题的方法，通过设定初始和末位的质心位置，假设初始和终止步态稳定，令边界c1=αn=0。但该方法没有考虑质心的初始速度且终止位置并不能保证其平衡，本文设定初始步态的前一步位置与当前位置相同，终止步态的下一步位置与当前位置相同，则有：

px(1)=(α1+β1)cx(1)+α1cx(2)

(11)

px(n)=αncx(n-1)+(αn+βn)cx(n)

(12)

1.4 摆动腿轨迹

正余弦函数、贝塞尔曲线都可以规划摆动腿轨迹。然而，双足机器人在步行过程中分为单腿支撑相和双腿支撑相2个阶段，只有当摆动腿起步和落地的速度、加速度都为零时，才能保证双足机器人在单腿支撑和双腿之间切换时保持稳定。为了得到更平滑的摆动腿轨迹，本文选择简谐运动合成的方法，其运动轨迹为:

(13)

(14)

其中,Dsw,Hsw分别为步长和抬腿的最大高度。

2 步态优化流程

2.1 步态参数选择和评价函数

2.1.1 步态参数选择

在基于CMA-ES[6]的步态训练中，为了优化出最优参数，双足机器人需要大量的重复训练，并通过评价函数评价此次训练参数的好坏。本文通过初始化双足机器人在球场的起始位置、训练周期以及训练时间，让机器人在快速模式下自主训练。如果当前训练的时间大于训练周期，则表示一个训练周期的完成，计算评价函数的值，并将评价函数的值带入到CMA-ES算法中得出下一个要训练的步态参数值，同时初始化起始位置并将当前的训练时间重置为0，进行下一个周期的训练。整个优化流程如图1所示。然而，其步态参数超过40个，将这些参数都进行优化很容易因空间巨大而影响收敛速度，因此，本文根据之前手动调试经验，选取影响步态稳定和速度的关键参数进行优化。所选的步态参数如表1所示。

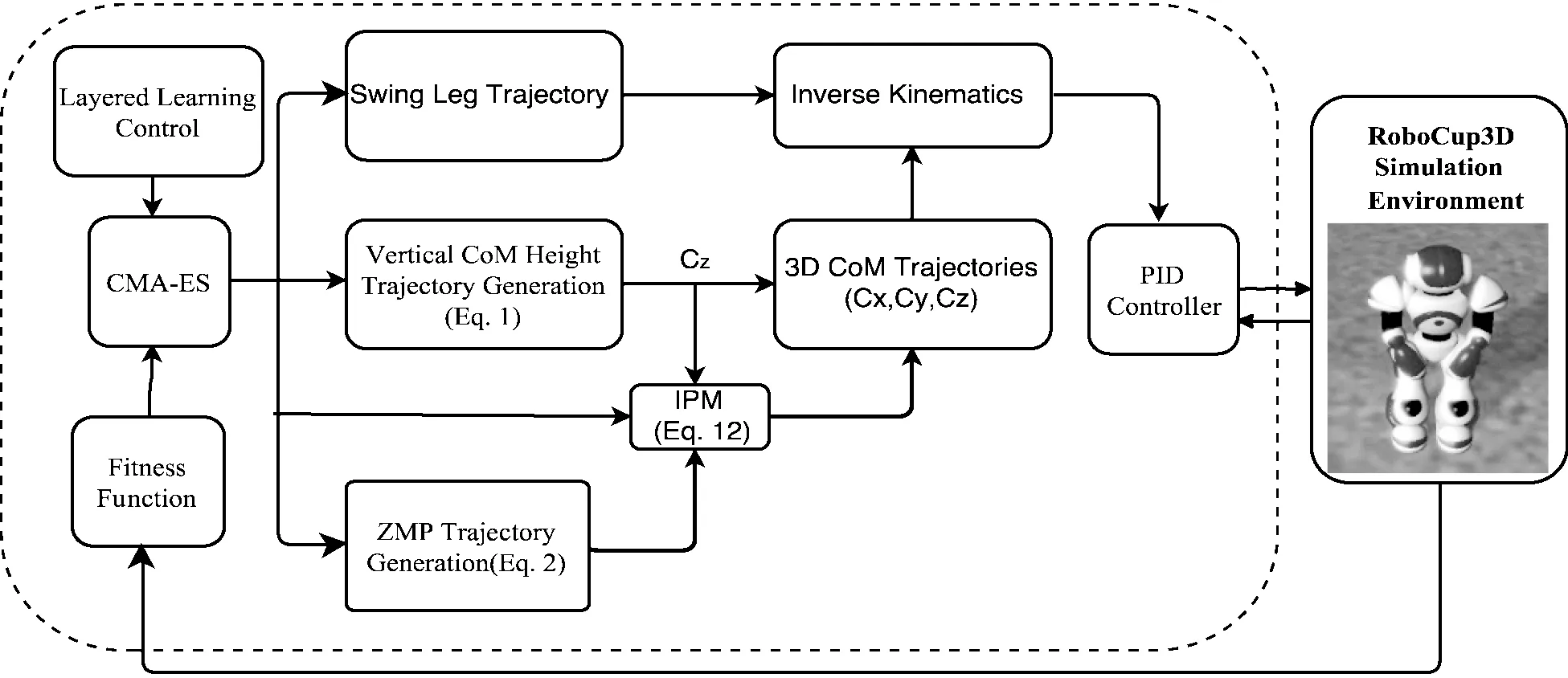
图1 步态优化流程

表1 需优化的步态参数

参数描述a0,a1,a2,a3,a4质心轨迹Ds,Dw步长和步宽Hs摆动腿抬脚的最大高度Sθ转身的角度Ts,Td步行周期和双足支撑时间commax快速停止时最大质心偏移量comerr减速时,质心最大偏移量Zmpoff支撑腿ZMP侧向偏移量xf双腿支撑初期质心与两脚中点的差值

每个步态参数都有约束条件，当参数越界时，一种常用的方法是在评价函数中增加一个惩罚项，使得搜索远离不可行的参数区域，另外一种方法通过转移参数位置使得参数满足约束条件。在本文中将采用S型函数转移参数位置：

(15)

其中,Min、Max分别为所设参数的最小值和最大值，wi为越界参数，wi+1为转移后的参数。

2.1.2 评价函数

在进化算法中，评价函数的好坏对优化结果起着重要的影响。本文通过如下标准判定训练结果的好坏：

1)在一个训练周期内，双足机器人所走的距离：

fdis=‖φend-φstart‖

(16)

其中,φstart为双足机器人训练的初始坐标点，φend为训练结束后的坐标点。

2)双足机器人在行走过程中，ZMP始终在支撑多边形框内。本文将选择步行动作序列中的ZMP坐标来评判步态的好坏[13]。

(17)

其中,pzmpx(k),pzmpy(k)为步行动作序列中实际ZMP坐标，px(k),py(k)为步行动作序列中所期待的ZMP坐标。

3)双足机器人在行走时，躯干保持稳定，身体不晃动。在双腿支撑初期，所期望的X轴方向质心坐标为两脚坐标的中点，但在训练中，所期望的质心坐标与实际质心坐标相比是有偏差的。因此，通过对比所期待的质心坐标与实际的质心坐标来判定双足机器人躯干是否保持稳定。

(18)

(19)

其中,xfootL,xfootR为双腿支撑初期X轴方向两只脚的坐标点，thθ为所设定的阈值，c为常数，fshake为惩罚值。

2.2 分层学习

在步态规划时，本文同时考虑步行的稳定性、速度以及灵活性。由于步态参数众多，只设置一个评价函数同时满足以上条件很难优化出最优值。因此，本文采用累积分层学习的思想[14]，先对双足机器人进行步态速度的训练。然后在之前优化的基本上进行双足机器人的稳定性训练，最后再进行灵活性训练。累积分层的过程如图2所示。

图2 步态分层优化过程

首先实现双足机器人直线优化，在步态优化前，根据之前手动调试的经验设置步态参数值，得到一个行走缓慢、稳定性差、频繁摔倒的双足机器人步态模式。设双足机器人的初始位置为(-10,0),8 s为一个训练周期，其评价函数为：

Fc1=γ1×fdis-γ2×fzmp-ffalling

(20)

其中,fdis为一个训练周期所走的距离，ffalling为双足机器人摔倒的惩罚值，若在一个周期内没有摔倒，则其值为0，fzmp为ZMP不在支撑多边形框内的惩罚值，γ1，γ2为权重系数。

在上一层学习中只考虑了双足机器人的步行速度，没有考虑稳定性。为了让双足机器人在行走时躯干保持稳定，在训练参数和任务不变的情况下，重新设计评价函数如下：

Fc2=γ1×fdis-γ2×fzmp-γ3fshake-ffalling

(21)

为了训练双足机器人的灵活性，将表1中所有参数进行优化，即在上一层优化的基础上增加双足机器人侧向和转向等相关参数，且侧向的最大距离为0.05 m，转身的最大角度为15°。在训练过程中设置2个不同的目标点让双足机器人进行步态学习，如果到达目标点则快速停止转向，进行下一个目标点的学习，其评价函数如下：

Fc3=γ1×fdis-ffalling-fpunish+freward

(22)

其中,freward表示在一个周期内完成任务的奖励值，若所剩的时间越多，则其值越大。若在周期内没有完成任务，则freward值为负。

3 实验结果

本次工作是在RoboCup3D仿真环境下测试NAO人形机器人步态完成，该机器人的原型是由法国Aldebaran-Robotics公司开发，实验平台是一个基于Spark以及开源物理引擎的三维模拟器rcssserver3d[15]，Farchy等人[16]的研究表明：经过不断的学习，优化出的仿真机器人步态参数可直接用在实体NAO机器人上。

3.1 实验1：可变的质心高度和ZMP轨迹对比验证

本文首先选择式(20)中的评价函数对双足机器人直线速度进行优化，其中垂直质心高度和ZMP轨迹分别为定值。图3是双足机器人优化后的摆动脚轨迹，摆动腿在起步和落地时运动轨迹与地面平行，保证了支撑腿之间切换的稳定性。经过多次测试求平均值，双足机器人在拥有固定的质心高度和ZMP轨迹时，其直线速度为0.67 m/s。为了验证本文所提的垂直质心高度和ZMP轨迹的有效性，在其他条件不变的情况下，优化式(1)和式(2)中的轨迹参数。最优适应度值轨迹变化如图4所示，随着迭代次数的增长，最优适应度值不断增加，最终迭代次数大约为85时收敛。双足机器人在拥有可变的质心高度和ZMP轨迹时，其速度达到0.73 m/s。垂直质心轨迹如图5所示。表2是优化后直线行走的部分步态参数。

图3 摆动腿轨迹

图4 评价函数收敛轨迹

图5 质心轨迹

表2 优化后的步态参数

参数优化值a00.1955a10.0759a2-7.3276a375.1340a4-204.0763Dsw/m0.148Hsw/m0.084Ts/s0.184

3.2 实验2：分层优化

经过上层学习，双足机器人直线步行速度有了很大提高，但行走时躯干晃动幅度较大，易出现步态震荡。因此，在双腿支撑初期，通过对比所期待的质心坐标与实际质心坐标的差值xf来进行稳定性学习，评价函数如式(21)所示。xf变化值如图6所示，在稳定步行阶段xf的值明显小于快速行走阶段的值，躯干晃动幅度较小。图7是双足机器人行走过程中的步态性能对比，与高稳定性模式相比，在快速行走模式下的相对质心落点变化幅度大，碰到障碍物易摔倒。

为了获得快速灵活、稳定的步态模式，本文在高稳定性步态模式的基础上进行步态的第三层学习，评价函数如式(22)所示。表3是优化后转向角的性能测试。初始角度表示双足机器人初始位置的身体朝向与目标点之间的角度。本文还跳过了快速、稳定步态模式的学习，以式(22)为评价函数，直接进行灵活性训练，结果表明优化后的机器人步态稳定性较差、易摔倒，证明了分层优化的有效性。

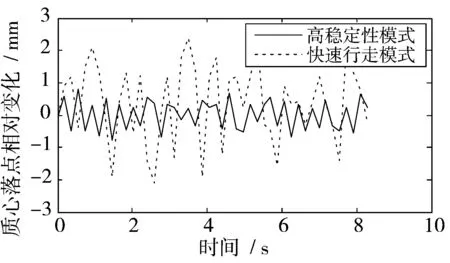
图6 步态稳定性检测

图7 步态性能对比

表3 转身性能测试

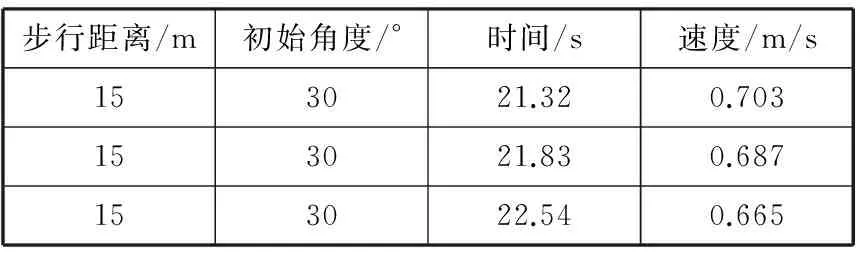
步行距离/m初始角度/°时间/s速度/m/s153021.320.703153021.830.687153022.540.665

3.3 实验3：验证多机器人环境下步态的稳定性、灵活性

本文采用Li等人[17]提出的蜂拥编队避障算法验证多机器人环境下优化步态的稳定性和灵活性。每个agent知道其邻域agent的位置和速度量化信息，且都有共同的虚拟领导者，基于排斥力和速度匹配的蜂拥控制器ui为：

(23)

其中，

(24)

N1(i)表示第i个agent排斥力邻域，N1(i)={j‖|xj-xi‖

r1，r2的值分别设为2 cm和6 cm，图8表示机器人的初始位置，标有数字的NAO机器人为训练对象，未标数字的NAO机器人为障碍物。图9表示快速行走的过程。图10表示快速行走中减速，避开障碍物的过程。图11是机器人终止位置，快速停止。整个过程没有发生跌倒和碰撞，且能够灵活地避开障碍物。经过多次测试，步态性能优于同样使用该蜂拥编队避障算法的CIT3D队[17]。

图8 训练时的初始位置

图9 时间t=9.5 s时的状态

图10 时间t=19.7 s时的状态

图11 时间t=31.2 s时的状态

4 结束语

本文提出一种双足机器人垂直质心高度可变的分层学习训练方法。通过规划ZMP和垂直质心轨迹，利用倒立摆模型和数值化方法控制零力矩点，运用CMA-ES算法进行训练，实现了双足机器人的类人行走。双足机器人在拥有可变的垂直质心高度和ZMP轨迹时，机器人的步行速度更快。本文的优化结果成功应用于河海大学Sainty3D仿真机器人足球队中，并连续获得2016,2017RoboCup世界杯中国赛3D仿真组季军和技术挑战赛冠军。已建立一套RoboCup3D机器学习训练框架，今后将优化机器人各种动作，如射门、传球等，加入新的智能优化算法与现有的CMA-ES算法进行比较，如指数自然进化策略、粒子群算法等。

[1] Graf C, Röfer T. A center of mass observing 3D-LIPM gait for the RoboCup standard platform league humanoid[C]// Springer Berlin Heidelberg: Robot Soccer World Cup. 2011:101-112.

[2] Kuo A D, Donelan J M, Ruina A. Energetic consequences of walking like an inverted pendulum: Step-to-step transitions[J]. Exercise and Sport Sciences Reviews, 2005,33(2):88-97.

[3] Guo Fayong, Zhao Jianghai, Mei Tao, et al. A modified gait generator for humanoid robots based on height compensation of center of mass[C]// 2014 IEEE International Conference on Robotics and Biomimetics(ROBIO). 2014:1278-1283.

[4] Hong Y D, Lee K B. Stable walking of humanoid robots using vertical center of mass and foot motions by an evolutionary optimized central pattern generator[J]. International Journal of Advanced Robotic System, 2016,13(1):27.

[5] Macalpine P, Barrett S, Urieli D, et al. Design and optimization of an omnidirectional humanoid walk: A winning approach at the RoboCup 2011 3D simulation competition[C]// Proceedings of the 26th AAAI Conference on Artificial Intelligence. 2012:1047-1053.

[6] Hansen N. The CMA Evolution Strategy: A Tutorial[EB/OL]. http://www2.fiit.stuba.sk/～kvasnicka/Seminar_of_AI/Hansen_CMA_tutorial.pdf, 2009-01-18.

[7] Shafii N, Aslani S, Nezami O M, et al. Evolution of biped walking using truncated fourier series and particle swarm optimization[M]// RoboCup 2009: Robot Soccer World Cup XIII. 2009:344-354.

[8] Kajita S, Nagasaki T, Yokoi K, et al. Running pattern generation for a humanoid robot[C]// Proceedings of 2002 IEEE International Conference on Robotics and Automation. 2002:2755-2761.

[9] Kagami S, Kitagawa T, Nishiwaki K, et al. A fast dynamically equilibrated walking trajectory generation method of humanoid robot[J]. Autonomous Robots, 2002,12(1):71-82.

[10] MacAlpine P, Depinet M, Stone P. UT Austin Villa 2014: RoboCup 3D simulation league champion via overlapping layered learning[C]// Proceedings of the 29th AAAI Conference Intelligence(AAAI-15). 2015:2842-2848.

[11] Shafii N, Lau N, Reis L P. Learning to walk fast: Optimized hip height movement for simulated and real humanoid robots[J]. Journal of Intelligent & Robotic Systems, 2015,80(3-4):555-571.

[12] Erbatur K, Kurt O. Natural ZMP trajectories for biped robot reference generation[J]. IEEE Transactions on Industrial Electronics, 2009,56(3):835-845.

[13] 李春光. 仿人机器人运动规划与蜂拥控制研究[D]. 无锡:江南大学, 2015.

[14] 蔡朝宏,江红. 一种双足步行的累积分层优化方法[J]. 小型微型计算机系统, 2013,34(5):1132-1136.

[15] Xu Yuan, Vatankhah H. Simspark: An open source robot simulator developed by the RoboCup community[C]// Proceedings of the 17th Annual RoboCup International Symposium. 2013:632-639.

[16] Farchy A, Barrett S, MacAlpine P, et al. Humanoid robots learning to walk faster: From the real world to simulation and back[C]// Proceedings of 2013 International Conference on Autonomous Agents and Multi-agent Systems. 2013:39-46.

[17] Li Chunguang, Tao Chongben, Liu Guodong, et al. Quantized flocking control for second-order multiple agents with obstacle avoidance[J]. Advances in Mechanical Engineering, 2016,8(1).