非线性尺度配准NLORB和亮度模板融合的方法

董 浩,吕东岳

(1.北京邮电大学网络技术研究院,北京 100876; 2.中国电子科技集团公司电子科学研究院,北京 100041)

0 引 言

进入21世纪，视频技术广泛应用于大家的日常生活。由于单台摄像机观察的范围有限，想要在不降低分辨率的基础上，拍摄的视频拥有较大视场，可以采用图像拼接的方法。图像拼接是计算机视觉领域的重要课题，作为图像处理的关键技术之一，它在全景视频、生物医学、警务侦查、地质勘测、机器人成像和目标识别等领域[1-3]都有广泛的应用。

图像配准是图像拼接的核心技术。文献[4]通过SIFT算法提取关键点，该算法在尺度和旋转变换的场景下有很好的鲁棒性。2011年，Rublee等人[5]提出了ORB算法，该方法的旋转和平移不变性较好，与SIFT和SURF[6]算法相比，其运算速度提高了一到两个数量级[7]。白雪冰等人[8]将鲁棒性优秀的SURF和ORB方法结合，改善了ORB算子的尺度不变性，提高了匹配的精度。李胜辉等人[9]提出C-ORB算法，其将颜色不变量与ORB算法结合，在不同光照强度和方向的场景下，提升算法的准确性与鲁棒性。

在图像拼接技术中，除了配准外，最重要的是图像融合技术。Szeliski[10]在前人基础上总结出帽子加权融合法，通过“帽状函数”来进行加权。以梯度域为基础的融合方法最早由Pérez等人[11]提出，通过梯度域，计算泊松方程，使得拼接结果中几乎没有缝隙。另一种融合算法是均值坐标(平面重心坐标)，Farbman等人[12]通过均值坐标得到的效果和泊松融合类似，效率却大大提高。

当前特征匹配算法存在很多问题，以SIFT为代表的高精度算法具有较好的匹配效果以及尺度和旋转不变性，但是时间复杂度高。以ORB为代表的速度型算法实时性较好，可是其尺度不变性较差。另外，图像融合方法也需要优秀的融合效果。

针对这些问题，在非线性尺度空间和ORB基础上，本文提出一种非线性尺度图像配准算法NLORB(Non Linear ORB)以及基于YUV亮度模板的均值坐标融合法，本文创新和改进点如下:

1)提出基于非线性尺度配准方法NLORB，建立非线性尺度空间，获得尺度不变性，保留比较清晰的边界信息。在多尺度空间内，进行非极大值抑制，提高配准成功率。

2)NLORB使用图像熵筛选符合条件的尺度参数，减少不必要的尺度层数，缩短配准时间。在特征检测时对特征点间距进行参数设置，比较均匀地分布特征点。

3)提出基于YUV亮度模板的均值坐标融合法，通过亮度通道初步叠加和直方图均衡化，改善了融合效果。

1 基于改进ORB算法的图像配准算法NLORB

1.1 ORB

ORB方法分为特征点提取、构造描述向量和特征点匹配这3个部分。在提取的时候，ORB通过FAST 9方法提取特征点，根据HARRIS响应对特征点排序，寻找极大值，与候选点P相邻8个候选点相比，若点P亮度值仍然是极大值(或极小值)，则视它为特征点。对于每个点，通过灰度质心法[13]，巧妙地利用其灰度与质心间的一个偏移向量来计算其主方向。

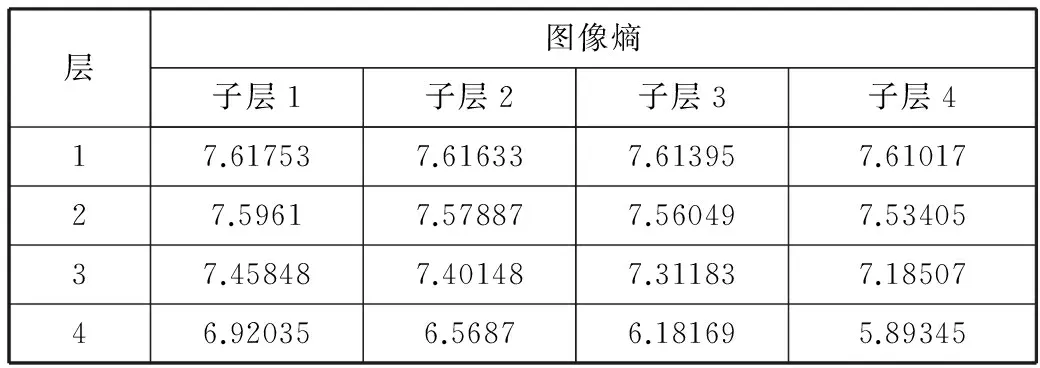
构造描述向量时，以特征点为中心，取S×S(31×31)的邻域，随机选取2个像素点x(u1,v1)和y(u2,v2)，比较两者亮度值。其中，p(x)，p(y)分别是随机点x=(u1,v1), y=(u2,v2)的像素值。若p(x)

B=b0b1…bi…bn

(1)

试验表明，n=128，256和512时，效率和正确率较高，一般n选256。试验使用候选点附近S×S(S=5)窗口的31×31像素点附近区域和积分图缩短所需时间，借助这几个步骤提高噪声变化的鲁棒性。

1.2 非线性尺度空间的NLORB

因为ORB算法不具备尺度不变性，所以本文基于ORB进行改进，提出非线性尺度配准方法NLORB，通过采用非线性尺度空间理论，获得尺度不变性，使用图像熵筛选符合条件的尺度参数，在特征检测时对特征点间距进行参数设置，均匀分布特征点,在多尺度空间内进行非极大值抑制，获得尺度不变性和鲁棒性较强的特征点，然后构造和匹配rBRIEF描述子，图1是配准算法流程。

1.2.1 建立非线性尺度空间

非线性尺度空间的数学模型可以用偏微分方程来建立，模型将图像亮度(L)对尺度的偏微分，看作某种传导函数的散度[14]，具体的方程如式(2)所示：

∂L/∂t=div(c(x,y,t)×▽L)

(2)

其中，时间t是尺度参数，div表示散度，▽表示梯度。传导函数c一般选用g3，其能够在有效平滑图像和消除噪声的基础上，保留比较清晰的边界信息。

非线性尺度空间可以划分为R层和R×S子层结构，参数σi可由式(3)计算：

σi(r,s)=σ02(r+s/S)

(3)

其中，σ0代表参数的初始值，(r,s)表示第r层s子层，S代表子层数。

基于像素的参数σi需要转换成尺度参数时间t，文献[4]表明，拥有尺度不变性的唯一线性卷积核是高斯核。高斯核对图像的处理，相当于对图像进行持续时间为t=σ2/2的非线性滤波[14]。依据以上内容，可以构建非线性尺度空间，获得等同于高斯尺度模型的尺度不变性。

1.2.2 尺度和特征检测参数设置

当尺度层数R比较大的时候，图像不清晰，其信息量不足，不利于后来的匹配过程。因此，为了选取合适的参数R，有必要先计算图像熵。

图像熵反映图像的平均信息量，表示某像素的亮度值与周围像素亮度分布的综合情况[15]。如果f是亮度函数[16]，f(i,j)为点(i,j)处的亮度值，1

(4)

(5)

图2 图像熵计算源图像

对图2构建非线性尺度空间，计算每层图像熵，如表1所示，选R=4，S=4。原图图像熵为7.63257，第4层第1子层图像熵为6.92035，大约为原图像的90%。因此，应选取层数R为3。

表1 各层图像熵

层图像熵子层1子层2子层3子层417.617537.616337.613957.6101727.59617.578877.560497.5340537.458487.401487.311837.1850746.920356.56876.181695.89345

在特征点检测时，通过设置特征点间的边缘阈值D，获得分布均匀的特征点集合。若D太大，特征匹配成功率降低；D太小，特征点分布会很密集。选择合适的D值很重要。本实验中，图像分辨率800×640像素，D值为7像素。

1.2.3 多尺度空间非极大值抑制

ORB算法对某候选特征点A进行非极大值抑制时，比较的范围是3×3邻域，即与A相邻的8个候选点。NLORB算法改进的地方在于，扩大比较范围，其包括与A同层的8个相邻点，以及与A相邻层对应的18个点。如果点A亮度值仍然是极大值(或极小值)，那么将它加入图像的特征点集合。

因此，在保留ORB算法耗时短和旋转不变性优点的同时，使用非线性尺度空间，改善ORB算法的尺度不变性，在消除噪声的同时，保持图像细节。利用图像熵，减少不必要的尺度层数，缩短配准时间。通过对特征点间边缘阈值的设置，使得特征点分布均匀。在特征检测阶段，对同尺度以及上下相邻尺度的27个候选特征点，进行非极大值抑制，提高配准成功率。

1.3 特征点匹配

Bolles等人[17]提出RANSAC鲁棒参数的随机采样一致算法，在特征点匹配的问题中被相当广泛地使用，它能够在很多错误匹配的场景中，计算出准确的图像变换矩阵，过滤错误匹配对，所以通过RANSAC这种拟合方法匹配特征点。

通过RANSAC过滤外点，计算变换矩阵参数。要达到降低RANSAC方法复杂度的目的，借助匹配的特征点间距、最近邻与次近邻间距比率和单应性参数测试筛选，使后面通过RANSAC匹配的准确率提高。匹配的特征点对间距为128，剔除不小于128的作为外点的特征点，最近邻与次近邻间距比率0.85，筛除大于0.85的部分，通过单应性参数测试查找能够对应的配准点，舍弃条件不适合的误配对，获得经过初筛的特征对集。

下面介绍RANSAC的流程，如果存在一个能够应用于全部准确特征点并且可以从特征点求解全部未知结果的模型，那么从全部特征点集中随机选取一些点组成子集，假如这个子集都是内点，通过子集求解RANSAC模型的参数，剔除这个模型的外点。接着通过不停地重复随机选取子集，寻找让外点数量最小的模型，那么它将被认为是最佳估计，所以可以在很多误匹配对中，剔除外点的干扰从而获得内点。

2 基于亮度模板的均值坐标融合法

2.1 亮度模板和直方图匹配

在视频拍摄过程中，接缝两边的图像可能由于光照等因素的影响，在亮度上呈现出细微的差别。而图像融合中主要完成的工作就是对接缝处实现自然过渡，最终得到平滑的图像。因此，融合图像的亮度函数的获取就非常重要。

首先将待融合图像A从RGB颜色空间转换到YUV，获取2幅待融合图像的亮度通道Y。文献[17]指出，RGB向YUV转换的代价比向HSI和HSV彩色空间的代价小。

获得图像A的亮度通道后，本方法将计算其直方图，然后和待融合图像B的亮度函数相加。直方图是图像中像素强度分布的图形表达方式,它统计了每一个强度值所具有的像素个数。如果图像B的亮度函数是LB(即Y通道)，A的直方图函数是Ha，融合后的亮度函数Lba可由式(6)计算。

Lba=addHist(LB, Ha)

(6)

其中，LB是待融合图像B的亮度函数，Ha表示待融合图像A的直方图函数，addHist是初步融合的叠加函数。接着对所得图像进行直方图均衡化，直方图均衡化是图像融合前有效的预处理工具。

2.2 泊松方程和均值坐标

Pérez等人[11]提出，通过梯度域，来计算泊松方程，实现融合的目标。如果将接缝一侧看作图像A，另一侧看成图像B，融合结果的边缘梯度值会和图像B对应位置相等，但是它核心部分的梯度值和图像A相等。根据上面的推断，通过求解限定迪杰特斯拉条件的泊松方程，在图像A和图像B的边缘进行插值，保证融合图像拼接处梯度值大致相等的目标。但是，该方法的时间复杂度较高。

均值坐标是一种针对插值问题的近似解法，可以加快计算泊松方程。假设闭合的2D多边形边界(逆时针方向)，则多边形内的某点x，它对边界∂P的均值坐标定义为：

(7)

wi=(tan(αi-1/2)+tan(αi/2))/‖pi-x‖

(8)

求解坐标λ后，需要对边界∂P函数进行插值运算：

(9)

其中，f(pi)取函数Lba的值。

2.3 色彩的融合和转换

最后，本文方法直接将图像的亮度函数LB用于色彩通道的均值融合处理，将融合结果从YUV转换为RGB颜色空间。

3 实验与结果

本文提出的配准方法NLORB和融合方法，通过OpenCV代码实现，电脑配置为:处理器为Intel酷睿i5，主频为2.6 GHz，内存4 GB，显卡为1 GB图形内存的NVIDIA GeForce GT980，硬盘为1 TB的计算机。操作系统为Win7 64位系统，编程环境为Visual Studio 2012。

3.1 尺度不变性对比实验

为验证NLORB算法的尺度不变方面的鲁棒性，以尺度不同的2幅图像作实验。图3(a)表示ORB的实验结果，在尺度变化较大的情况下，ORB的配准效果不是很理想，在书籍边缘的一些地方存在明显的匹配错误；用SIFT测试的结果如图3(b)所示，SIFT的配准效果比ORB好一些；采用NLORB算法的实验结果如图3(c)所示，特征点分布比较均匀，获得较好的匹配效果。图3(d)表示结合SURF改进ORB算法的实验结果，匹配对的数量最少，分布零散，仍然有一些错误匹配对。图3(a)、图3(b)、图3(c)和图3(d)进行对比表明，本文NLORB算法在尺度不变方面鲁棒性比ORB更强，匹配2幅尺度差异较大的图像时，配准效果仍然良好。

(a) ORB

(b) SIFT

(c) NLORB

(d) 结合SURF改进ORB图3 尺度变换实验

接下来，使用ORB，SIFT，NLORB和SURFORB算法对实验中的配准数据分别进行统计，对实验结果定量分析，如表2所示。实验数据表明，相比于ORB方法，本文NLORB算法提高匹配对的质量和成功率，且成功率方差较小。

表2 尺度变化时匹配对比

算法匹配对数匹配成功对数成功率/%ORB553767.31SIFT777698.70NLORB484593.75SURFORB403792.50

3.2 旋转不变性对比实验

本文NLORB算法，继承了ORB算法的旋转不变性，使用不同旋转的2幅图像作为对比测试对象。用ORB,SIFT,NLORB和SURFORB测试的结果如图4(a)～图4(d)所示。

(a) ORB

(b) SIFT

(c) NLORB

(d) 结合SURF改进ORB图4 旋转变换实验

用ORB,SIFT,NLORB和SURFORB算法分别对实验中的配准数据进行统计和定量分析，如表3所示。对比图4(a)、图4(b)、图4(c)与图4(d)和表3可以发现，在旋转变化的场景下，NLORB配准成功率比ORB提高5.5%，特征点分布更均匀。

表3 旋转变化时匹配对比

算法匹配对数匹配成功对数成功率/%ORB12910883.72SIFT12511995.20NLORB655889.23SURFORB595491.53

3.3 匹配时间对比实验

与SIFT比较，NLORB算法配准特征检测和描述时间较短。以第一组尺度变换图片作为实验对象，用ORB,SIFT,NLORB和SURFORB对实验中的配准时间数据分别进行统计，如表4所示。

表4 配准时间对比

算法图像特征检测时间/ms特征描述时间/msSIFTBook1205.443212.998Book2124.434325.979ORBBook1147.43411.041Book216.14812.549NLORBBook1142.7427.461Book276.5336.857SURFORBBook1137.0497.500Book271.1277.726

从特征检测时间上看，SIFT匹配时间最长,NLORB,SURFORB和ORB耗时相对较少。从描述时间和匹配时间上看，NLORB,SURFORB与ORB算法耗时小于SIFT算法。因此，从数据上直观显示，NLORB算法速度比SIFT算法快，比ORB算法慢一些，与SURFORB相当。

综上，NLORB具有特征点分布较均匀、匹配速度较快和配准成功率高的优势。该算法特征检测、描述和匹配速度比SIFT快，比ORB和SURFORB算法略慢，大部分场景下，匹配成功率比其他2种算法高，适合尺度变换和旋转变换的场景。

3.4 图像融合实验

多路视频图像通过基于HSI和YUV亮度模板的均值坐标融合法这2种方法进行图像融合。

图5 基于HSI亮度模板的均值坐标融合法的效果

图6 基于YUV亮度模板的均值坐标融合法的效果

图5和图6表示了基于HSI和YUV亮度的均值坐标融合法的拼接结果，其中HSI亮度模板均值融合法的效果有待提高，部分拼缝两侧有明暗差异。相比较而言，基于YUV亮度模板均值坐标融合法的融合结果代价较小，并且拼接两侧的亮度和色彩通道过渡非常自然。

4 结束语

本文提出基于非线性尺度空间的配准方法，通过建立非线性尺度空间，使用图像熵筛选符合条件的尺度参数，设置特征点间距，特征检测时在多尺度空间内对候选点进行非极大值抑制，获取稳定的特征点。仿真结果表明，对于图像存在尺度和旋转变换的场景，本文方法有效地改善ORB算子的尺度不变性、分布均匀性和鲁棒性，匹配效果相对较好，且配准时间小于SIFT。

另外，本文提出基于亮度模板的均值坐标融合法,将待融合图像从RGB颜色空间转换到YUV，通过其亮度通道计算直方图，进行匹配加成，通过坐标均值法融合原图像，与HSI均值坐标融合法相比，提高了融合效果。

[1] 杜承垚,袁景凌,陈旻骋,等. GPU加速与L-ORB特征提取的全景视频实时拼接[J]. 计算机研究与发展, 2017,54(6):1316-1325.

[2] 张莹,闫璠,高赢,等． 基于ORB算法和OECF模型的快速图像拼接研究[J]. 计算机工程与应用, 2017,53(1):183-189．

[3] 刘海燕,杨昌玉,刘春玲,等． 基于梯度特征和颜色特征的运动目标跟踪算法[J]. 计算机应用, 2012,32(5):1265-1268．

[4] Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004,60(2):91-110.

[5] Rublee E, Rabaud V, Konolige K, et al. ORB: An efficient alternative to SIFT or SURF[C]// Proceedings of 2011 International Conference on Computer Vision. 2011:2564-2571.

[6] Bay H, Tuytelaars T, Gool L V. SURF: Speeded up robust features[C]// Proceedings of the 9th European Conference on Computer Vision. 2006:404-417.

[7] 索春宝,杨东清,刘云鹏. 多种角度比较SIFT、SURF、BRISK、ORB、FREAK算法[J]. 北京测绘, 2014(4):23-26．

[8] 白雪冰,车进,牟晓凯,等． 结合快速鲁棒性特征改进ORB的特征点匹配算法[J]. 计算机应用, 2016,36(7):1923-1926.

[9] 李胜辉,史瑞芝,叶辉. 结合颜色不变量和ORB特征的图像匹配算法[J]. 包装工程, 2016,37(15):18-23．

[10] Szeliski R. Video mosaics for virtual environments[J]. IEEE Computer Graphics and Applications, 1996,16(2):22-30.

[11] Perez P, Gangnet M, Blake A. Poisson image editing[C]// ACM SIGGRAPH 2003 Papers. 2003:313-318.

[12] Farbman Z, Hoffer G, Lipman Y, et al. Coordinates for instant image cloning[C]// ACM SIGGRAPH 2009 Papers. 2009:67.

[13] 王冰,职秦川,张仲选,等. 灰度图像质心快速算法[J]. 计算机辅助设计与图形学学报, 2004,16(10):1360-1365．

[14] Alcantarilla P F, Bartoli A, Davison A J. KAZE: Features[C]// Proceedings of the 12th European Conference on Computer Vision. 2012:214-227.

[15] 白雁力,周信东． 基于区域最大图像熵的车牌二值化算法[J]. 电视技术, 2011,35(21):128-130.

[16] 龚萍,张辉,毛征,等． 融合局部熵二维熵的空中目标跟踪算法研究[J]. 国外电子测量技术, 2014,33(1):32-35.

[17] Fischler M, Bolles R. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981,24(6):381-395.

[18] 柳杨,顾昭艺. 彩色图像直方图均衡算法性能分析[EB/OL]. http://www.paper.edu.cn/releasepaper/content/201104-377, 2011-04-18.