初中数学分式化简求值的技巧总结分析
江苏省苏州市吴江区芦墟初级中学 潘 琪
初中数学课程教学中关于分式部分的内容,是学生需要重点把握的知识内容,分式化简求值需要学生对复杂的分式进行化简,在结构分析和数学关系的分析中,掌握求值方法和求值技巧。由于初中学生在分式化简求值中存在技巧方面的不足,解题效率不高,本篇文章在此基础上,重点对初中数学分式化简求值的相关技巧性内容进行研究与分析,关于初中数学分式化简求值的几种有效解题方法和技巧等主要从以下几个方面展开研究与探讨:
一、去分母计算
分式化简求值的过程中需要对结构形式较为复杂的分式进行化简,对分式中的分母部分进行通分、约分,化简转化为整式,更加有利于简便运算。

在这道题的解答中,需要先对分式进行观察,由于等式两边的分式分母不同,分别为(x+1)和(3x+3),要方便分式运算,可以将(3x+3)化简为3(x+1)。左边分式的分子、分母分别乘以3,分子部分为3x,分母部分同右边分式分母部分,即为3(x+1),右边分式部分的分子部分为2x,常数项部分化为分式形式,分子、分母均为3(x+1),则分式进一步化简为3x=2x+3(x+1),即可进入下一步的问题解答。去分母的分式化简方法在分式计算中的应用较为常见,将分式化简为整式形式,计算更加简便,并且也不会产生丢项、漏项等问题,但是在此过程中,需要注意分式去分母的过程中,需要分子和分母均同时除以或乘以某个数或某个项,否则会影响最终的计算结果。
二、合并同类项计算
分式化简求值中使用合并同类项的方法,也能够简化运算过程,合并同类项是根据乘法运算中的乘法分配律,对于同类项的系数部分进行相加,然后将得到的结果部分作为系数,但是指数部分和字母部分仍旧不变。合并同类项在分式化解求值中的应用属于乘法分配律的一种逆运算,例如:3a,2a和5a均属于同类项,a2和-5a2、-ab2和4ab2也是同类项,所有的常数也都是同类项,合并同类项在分式化简求值中运用可以将相同的项合并,减少项数,简化分式结构,使分式计算更加简便。
由于这道题中含有四个不同的分式参与加减运算,直接对其通分,化成同分母的分式相加减,考虑到公分母的复杂度较高,可以把前两个分式先相加,在通分运算中对同类项部分进行合并,即可完成题目的解答。具体的解答过程如下:
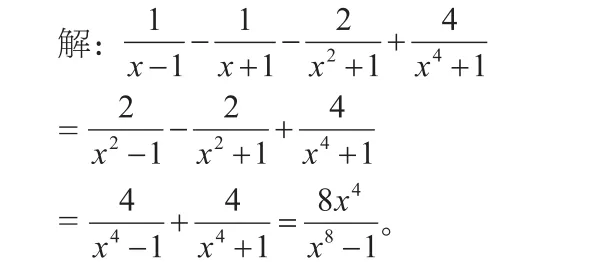
在这道题的解答中,对于前两项分式,分母部分分别为x-1和x+1,两边可以化为(x-1)(x+1)=x2-1,先完成运算,然后对于后面的分式部分也可以以此类推,分别通分、化简、运算和求值。合并同类项的分式化简方法也比较常用,但是老师在教学中需要引导学生注意每个项的特点,对其中的常数项部分和字母项部分均需要观察仔细,否则合并的不是同类项,导致最终的解答结果不正确,同时,对于移项和合并同类项,要注意正负号的变化。
三、分式化简求值的方法技巧总结
初中数学课程教学中,老师主要是对学生进行基础知识教学,分式部分是数学课程中的重要教学组织部分,学生需要在分式概念和基本结构形式的了解中,掌握分式化简求值的有效方法。分式化简求值是根据数学运算方法和定律,对分式进行化简,使运算过程更加简便。分式化简方法包括去分母化简和合并同类项化简,这两种化简方法比较常用,分式在化简后,项数减少,结构形式一目了然,数学关系更加明确,分式方程的解答也更加简便,初中学生在实际的学习中需要注意自我总结和归纳,加强自主学习。
初中阶段的数学课程教学对于学生的数学基础知识掌握和数学能力培养等具有重要的作用,在实施教育教学的过程中,对于分式化简求值的内容,需要老师在课堂实践中根据学生的具体学习情况,向学生进行分式化简求值解题技巧方面的讲解。分式化简求值是对复杂的分式进行化简,以约分的方法简化分式结构,分式化简方法包括去分母化简、合并同类项化简,分式化简后分式的项数减少,能够为方程解答提供便利。其中,去分母化简分式是对分式方程进行“去分母”,将分式方程化简为整式方程,这也是分式化简求值的简要方法之一;而合并同类项化简分式,则是对分式中的同类项进行合并运算,属于分配律的逆运算。初中数学课程教学中,老师通过例题讲解和分析的形式引导学生对分式化简求值的方法和技巧进行归纳和总结,能够更加有效地提升学生的运算思维转换能力和解题效率。
[1]邵伟.分式化简求值中的数学思想[J].中学生数理化(教与学),2011(06).
[2]饶敏.分式的化简及求值技巧[J].初中生辅导,2010(11).
[3]左加亭.分式求值方法多[J].中学生数理化(八年级数学)(人教版),2010(01).
[4]朱家海.分式化简求值的若干方法与技巧[J].数理化学习(初中版),2009(09).

