一道测试题的教学与思考
江苏省江阴市青阳中学 王士勇 谭 颖
每学期临近期末,按照学校的要求,师生都要有计划地开展期末复习工作,学生必定会做一定量的模拟测试题,教师必定要进行试卷评讲,那么试卷评讲课应该怎么上呢?常见的有以下三种方式:1.就题讲题,普遍答错的题重点讲,少部分人答错的题少讲或不讲;2.有辨别地选择典型题型讲解,并配以同类型的题进行巩固;3.以上两种方式兼有,更注重解题策略与数学思想的渗透。
虽然以上方式中,教师会注重师生互动,但主要是教师为主,学生为辅的教学模式,这样的试卷讲评课模式显然不符合新课改的要求,新课改的六项目标主要包括(下称“目标”):改变课程实施过于强调接受学习、死记硬背、机械训练的现状,倡导学生主动参与、乐于探究、勤于动手,培养学生搜集和处理信息的能力、获取新知识能力、分析和解决问题能力以及交流与合作能力。笔者也在追问自己:试卷讲评课究竟该怎么上?怎样实施才会更有效地服务于“目标”?
带着这些问题,笔者不断在实践中探索与尝试,有了些点滴体会,不当之处,敬请批评指正。
一、学情调查
例题:已知函数f(x)=lnx-a2x2+ax(a∈R)。
(1)当a=1时,求函数的单调区间,并证明函数f(x)只有一个零点;
(2)若函数f(x)在区间(1,+∞)上是单调减函数,求实数a的取值范围。
这是笔者所在学校期末复习期间的一道检测试题,此题侧重于“双基”的考查,难度适中,思路宽广,学生极易上手,应该可以轻松完成。试卷批阅后发现,第(1)小题几乎没有学生出错,但第(2)小题,50人中有21人出错,大大超出了笔者的预期。笔者随即将答卷分发给各学习小组,要求各小组利用课余时间对此题的第(2)小题进行学情分析,并提交学情报告(因为笔者是班主任,经常带领学生分小组研究一些学科或非学科的问题,并提交研究报告)。根据学生小组提交的报告,笔者精心设计了一堂试卷讲评课。
二、教学过程
为了鼓励小组学习,教师首先展示了学生研究报告,表格如下:
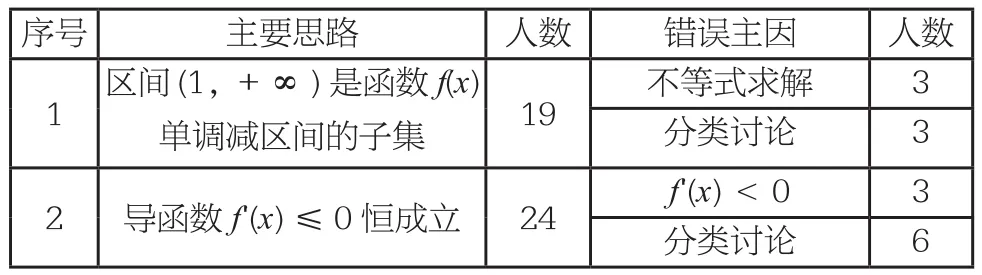
序号 主要思路 人数 错误主因 人数1 区间(1,+∞)是函数f(x)单调减区间的子集 19 不等式求解 3分类讨论 3 2 导函数f'(x)≤0恒成立 24 f'(x)<0 3分类讨论 6

3 对函数f(x)二次求导 5 对f'(x)再优化 4 4其他 2 多种因素 2
1.不识庐山真面目
本题第(2)小题是一道利用导数研究函数单调性问题的题型,应该是极易上手的,但从批阅情况来看,结果并不理想。
学生1:基于区间(1,+∞)是f (x)在定义域(0,+∞)内单调减区间的子集,

②当a>0时,令f'(x)<0,∴(2ax+1)(ax-1)>0,解得或
教师:学生1的解答是对表格中思路1的完美演绎,抓住参数对导函数正负的影响这一本质进行了分类讨论,不仅回答了有些学生对此题不会分类讨论的疑惑,而且指明了解不等式出错的原因所在,非常好!实际上,课本是我们最好的指导老师,本题我们可以在课本中找到“题根”,参看苏教版高中数学(选修2-2)第28、29页例题1、2、3。那么,我们还可以怎么理解函数在给定区间上是单调的呢?
学生2:f (x)在区间(1,+∞)上是单调减函数可转化为f'(x)≤0在(1,+∞)上恒成立,但对我不会处理了。
学生3:可以把f '(x)≤0转化为2a2x2-ax-1≥0在(1,+∞)上恒成立,令g(x)=2a2x2-ax-1,则有gmin(x)≥0。
①当a=0时,则-1≥0,显然不成立;
教师:学生2对导函数的处理没有把握好,太可惜了。学生3通过层层剥离发现,它是求含参一元二次函数的最值问题,如何分类讨论也就迎刃而解了,值得表扬!那么,为什么会有人写成f'(x)<0呢?
教师带领学生重温了苏教版高中数学(选修2-2)第28页的思考,学生明白:函数图象上任一点是无单调性的,一定要注意它对导数的影响。
随着分析的深入,学生已经注意到导函数对单调性的影响,教师继续追问学生:还能有其他解法吗?
学生4:受学生2的启发,我想把f '(x)的最大值求出,所以我想到了对f '(x)再求导。

教师:学生4的解法告诉我们:既然导函数也叫函数,那么我们为什么不能对它再求导研究呢?这就是我们曾经介绍的“二次求导”。
此时教师观察到学生们眼睛一亮,似有所悟,便继续发问:为什么有学生对学生3解法中的再求导没有做出来呢?自此,学生终于明白:导函数的优化选择很重要。教师再追问:这种做法真的不能求出结果吗?由于有了上面知识的铺垫,教师估计学生能够解决,便把此问题作为课后作业。
2.数形结合莫相忘
教师为了激发学生的思维灵感,引用了华罗庚教授曾说的一段话:“数与形,本是相倚依,焉能分作两边飞;数无形时少直觉,形少数时难入微,数形结合百般好,隔离分家万事休;切莫忘,几何代数流一体,永远联系莫分离。”那么能否从形的角度探寻问题的本质呢?学生进行小组探讨,并通过实物投影展示讨论成果。
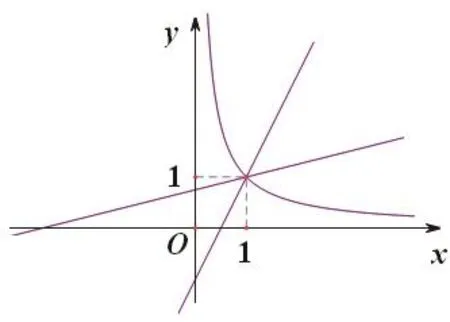
教师:此法是从“形”的角度揭示了本题的内在特点,正所谓数形结合,相得益彰,往往会产生1+1>2的功效,不正是创造性思维的原动力吗?
本题为什么会有那么多人出错?问题的根源正是学生对导函数没有进行细致入微地研究,不识庐山真面目,太可惜了!
3.更上一层楼
若教学活动到此为止,那就好比夜晚的烟火,虽绚丽夺目,但好景不长。为了激发学生的求知欲、创新欲以及在学生心中构建起系统的认知结构,教师又带领学生去拟制试题和感受高考。
(1)拟题
题1:已知函数f (x)=lnx-a2x2+ax(a∈R),若f (x)在区间(1,+∞)上存在单调递减区间,求实数a的取值范围。
题2:设函数f (x)=x3-ax2+a2x+1,g(x)=ax2-2x+1,a∈R,若f (x)与g(x)在区间(a,a+2)上均为增函数,求a的取值范围。
(2)感受高考
题1:(2014·新课标全国卷Ⅱ高考文科数学·T11改编)若函数f (x)=kx-lnx在区间(1,+∞)上单调递增,求k的取值范围。
题3:(2013·江苏高考数学·T20)设函数f (x)=lnx-ax,g(x)=ex-ax,其中a为实数。
(1)若f (x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围;
(2)若g(x)在(-1,+∞)上是单调增函数,试求f (x)零点的个数,并证明你的结论。
题4:(2011·江苏高考数学·T19)已知实数a,b是实数,函数f (x)=x3+ax,g(x)=x2+bx,f '(x)和g'(x)是f (x)、g(x)的导函数,若f'(x)g'(x)≥0在区间I上恒成立,则称f (x)和g(x)在区间I上单调性一致。
(1)设a>0,若f (x)和g(x)在区间[-1,+∞)上单调性一致,求b的取值范围;
(2)设a<0,且a≠b,若函数f(x)和g(x)在以a,b为端点的开区间上单调性一致,求的最大值。
通过拟题,学生不仅巩固了知识,而且升华了认知,更对自己的奇思妙想感到欣喜,变学数学为“玩”数学,寓创新于其中,体会不一样的乐趣。通过感受高考,学生为自己拟题点赞,更会明白:原来高考题就扎根于书本,孕育在基础知识之中。让高考不再那么高不可攀,神秘莫测,多了几分亲近,更接地气,原来高考题可以这样获得,同时也给学生课后作业和再探索留下了空间。
三、关于教学的思考
关于试卷讲评课,笔者以一道测试题为突破口,对试卷讲评课的有效模式做了一次尝试,并用一个“动”字来概括这次尝试,不仅新授课需要“动”,试卷讲评课也需要“动”,这里所说的“动”有显性和隐性之分,简称为“双动”。
1.显性的“动”
《普通高中数学课程标准(实验)》中指出:“高中数学课程应力求通过各种不同形式的自主学习、探究活动,让学生体验数学发现和创造的历程,发展他们的创新意识。” 故显性的“动”就是学生的“学习主动”,它是学生行为。学生在“学习主动”中获得知识、技能以及养成数学素养。在这节课中,学生要做到三“动”:课前学情分析、课堂以问题链为驱动的启发与探究、课后作业与再探究。笔者的意图很明显,通过三“动”,使学生逐渐学会用数学的观点来分析问题、探究问题和解决问题的问题策略以及基于数学素养的数学学习。罗增儒教授曾说:“学生逐步学会用数学的眼光观察世界,发展数学抽象、直观想象素养;用数学的思维分析世界,发展逻辑推理、数学运算素养;用数学的语言表达世界,发展数学建模、数据分析素养。增强创新意识和数学应用能力。”让显性的“动”真正起到主动学习之功效。
2.隐性的“动”
《普通高中数学课程标准(实验)》中也指出:“学生的主动学习过程成为在教师引导下的“再创造”过程。”这里的“教师引导”就是隐性的“动”,它是教师行为,包含了两个方面:一是教师对有效教学活动的构思;二是教师对有效教学活动的实施。在这节课中,笔者在学生显性的“动”上下足了功夫,如从课前学情分析、课堂以问题链为驱动的启发与探究、课后作业与再探究等教学活动的构思到实施,无不体现教师隐性的“动”。真正使教师隐性的“动”起到激发学生学习数学的兴趣、树立学生学好数学的信心、逐步养成用数学思维解决问题的习惯之功效。
[1]罗增儒.从数学知识的传授到数学素养的生成[J].中学数学教学参考,2016(7):2-7.

