Study on Vulnerability Criteria and Model Experiment for Surf-Riding/Broaching
GU Min,CHU Ji-long,HAN Yang,LU Jiang
(1.China Ship Scientific Research Center,Wuxi 214082,China;2.Jiangsu Key Laboratory of Green Ship Technology,Wuxi 214082,China)
0 Introduction
The second generation intact stability criteria for five stability failure modes including pure loss of stability,parametric roll,surf-riding and broaching,dead ship condition and excessive accelerations are under development at the International Maritime Organization(IMO)to guarantee sufficient safety of ships in waves[1].The second generation intact stability criteria consist of two levels of vulnerability criteria based on simple physical models and direct stability assessment using advanced numerical simulation methods.
Surf-riding occurs when a ship is captured by a wave from the stern and forced to run with wave celerity.During surf-riding,the ship is often unstable and will turn uncontrollably despite keeping maximum rudder angle in the opposite direction,which is defined as broaching.Broaching is considered as one of the most dangerous phenomena in following and sternquartering waves for high-speed ships,such as destroyers and fishing vessels.
Levels 1 and 2 vulnerability criteria for surf-riding and broaching have been determined at the 3rd session of Sub-committee on Ship Design and Construction(SDC)[2-3].Because surfriding is usually regarded as a precondition of broaching,the likelihood of surf-riding occurrence is used as vulnerability criteria instead of broaching.Level 1 criterion is simply checked by ship speed and length.The formula of level 2 criterion is obtained by using Melnikov method,the stochastic wave theory and the wave statistics,and the calculated value need to be compared with the safety level set as 0.005 currently.
It is important to estimate surf-riding thresholds in the level 2 criterion.Recently some approximate formulas based on Melnikov’s method were proposed to predict surf-riding thresholds in following regular waves[4-7].Maki et al[6-7]also provided another analytical formula for calculating surf-riding thresholds using a continuous piecewise linear approximation,which is more transparent than Melnikov’s method in obtaining the solution.
The prior task of IMO SDC 4 was drafting the guidelines for the specification of direct stability assessment procedures[1].For the numerical simulation of surf-riding and broaching,the numerical approach is required at least a 4 DOF mathematical model of surge-sway-rollyaw motion,and hydrodynamic forces should consider hydrodynamic lift forces due to the coexistence of wave particle velocity and ship forward velocity.
Umeda and Hashimoto[8]used a 4 DOF mathematical model of surge-sway-roll-yaw motion to qualitatively explain the capsizing phenomena associated with surf-riding and broaching in regular following and stern-quartering waves.In order to improve the calculation accuracy to realize quantitative prediction,Hashimoto et al[9-10]took into account several important nonlinear terms in the previous mathematical model.
For the numerical simulation in irregular waves,the issue is how to identify surf-riding and broaching in irregular waves.Belenky et al[11]proposed a method to detect surf-riding in irregular waves by the celerity of irregular waves,which is computed by finding the point of maximum wave steepness on the down slope of the wave nearest the ship[12].They also provided two novel metrics for likelihood of surf-riding and broaching used for evaluating the probability of surf-riding and broaching in irregular waves[13-14].
In order to verify the applicability of vulnerability criteria for surf-riding and broaching,the calculations for seven sample ships including one unconventional ship are conducted.The free running experiment with the unconventional ship is carried out to provide validation data for criteria check.
1 Assessment on vulnerability criteria for surf-riding and broaching
According to the updated drafts[2-3,15],vulnerability criteria for surf-riding and broaching are simply introduced as follows.
1.1 Level 1 criterion
A ship is judged to be vulnerable to the surf-riding and broaching failure mode if formula(1)is false:

1.2 Level 2 criterion
A ship is judged to be vulnerable to the surf-riding and broaching failure mode if the value C is larger than 0.005:


where Fncris the critical Froude number corresponding to the surf-riding threshold for the regular wave with steepness sjand wavelength to ship length ratio ri,and calculated by using the critical speed ucr,which is determined by solving the following equation:

where Teis the propulsor thrust in water;R is the calm water resistance of the ship;ncris the commanded number of propeller revolutions corresponding to the surf-riding threshold,which is estimated based on Melnikov method.The detailed estimation of ncris introduced in the draft explanatory notes for surf-riding and broaching[3].
1.3 Sample ships calculation
The check of level 2 criterion for a fishing vessel is conducted to compare with the example in the draft explanatory notes for surf-riding and broaching[3],and the comparison results of Fncrand the value C are shown in Tabs.1-2 repectively,which indicate that the software coded by the authors based on the updated vulnerability criteria for surf-riding and broaching[2-3,15]has sufficient accuracy.As shown in Tab.3,the sample calculations for seven ships are conducted to analyze the applicability of the current vulnerability criteria for surfriding and broaching.
从表4可以看出,29家医养结合型养老机构中的20家综合效率值为1,视为DEA有效,另外9家处于弱DEA有效,即在规模效率或纯技术效率值上没有达到最优,其中,最低的是机构10,其综合效率仅为0.675,相对于其他养老机构而言,其投入的资源没有得到充分利用。在规模报酬可变的情况下,纯技术效率值为1的有23家,占比79.31%;而从规模效率角度分析,20家规模效率有效,9家处于规模效率无效的状态,还存在通过改变规模提高效率的空间。
The results of the sample calculations show that five ships fail to pass level 1 criterion,which need to check level 2 criterion,because their Froude numbers are larger than 0.3,while their lengths are less than 200 m.Three ships with much higher speed still can not pass level 2 criterion,which need to be checked by the direct stability assessment.

Tab.1 Comparison results of Fncr

Tab.2 Comparison results of the value C
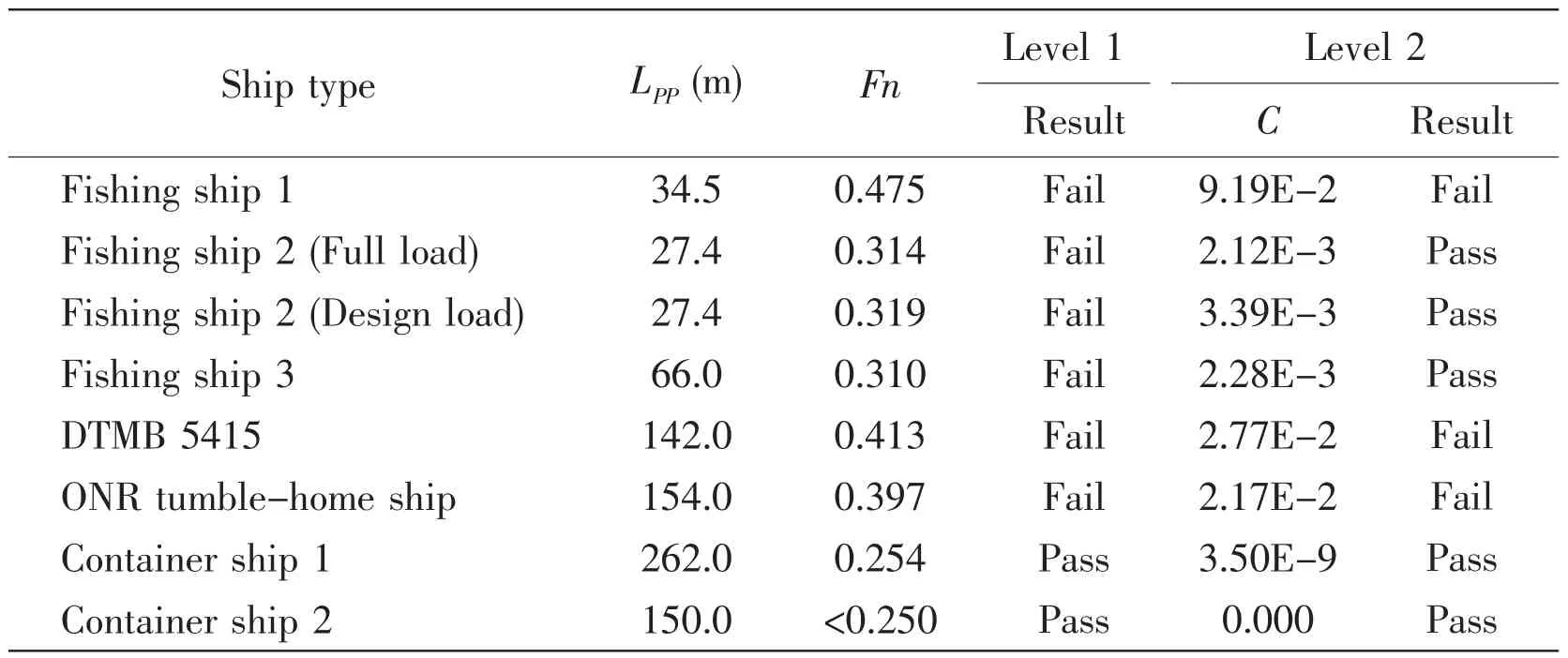
Tab.3 Summary of sample calculations
There are no inconsistencies in the checks between two levels vulnerability criteria,which indicate that the mathematical model of the current level 2 criterion is reasonable.
In order to provide validation data for the calculation of vulnerability criteria,ONR tumblehome vessel as an unconventional ship with good performance of propulsion and seakeeping,which is one of standard models for the second generation intact stability criteria,is used as a subject ship in the following model experiment.
2 Experimental investigation
2.1 Experiment
The free running experiment of the ONR tumblehome vessel was conducted to assess the surf-riding and broaching phenomena in regular following and stern-quartering waves at the seakeeping basin of China Ship Scientific Research Center(CSSRC).The basin is 69 m length,46 m breadth and 4 m water depth,which is equipped with flap wave makers at the two adjacent sides of the basin.The ship model was equipped with double propellers and double rudders.Ship motions were measured by the MEMS(Micro Electro-Mechanical System)-based gyroscope placed on the ship model.
The principal particulars and the body plan of the ONR tumblehome vessel are shown in Tab.4 and Fig.1.

Tab.4 Principal particulars of ONR tumblehome vessel

Fig.1 Body plan of ONR tumblehome vessel
2.2 Results and discussions
As shown in Figs.2-3,the ship experiences surf-riding and broaching in two wave conditions,respectively.Surf-riding and broaching often occur on the down slope of a wave,and broaching always accompanied with a large heel angle,may lead to stability failure,or even capsizing.

Fig.2 A snapshot of surf-riding in the experiment

Fig.3 A snapshot of broaching in the experiment
The experiment results in following waves are shown in Figs.4-5.The pitch motion of the ship appears periodic at the beginning,and then the amplitude of pitch motion is almost unchanged in later time,while yaw motion is generally small all the time.This reveals that stable surf-riding occurs.
With the wave steepness increasing and the heading changing to stern-quartering waves as shown in Figs.6-7,surf-riding occurs quickly.Then the ship can not keep its course even with maximum steering effort,and broaching occurs.At the same time,roll angle increases rapidly.But with the action of rudders,the ship is stable at a new heading temporarily.And then the ship is captured again by a new wave and surf-riding and broaching occur once more.At the third broaching event,the roll angle is so large that the ship capsizes at last.

Fig.4 Time histories of pitch and roll angles(Fn=0.4,λ/L=1.25,H/λ=0.05,following waves χ=0°)

Fig.5 Time histories of yaw and rudder angles(Fn=0.4,λ/L=1.25,H/λ=0.05,following waves χ=0°)
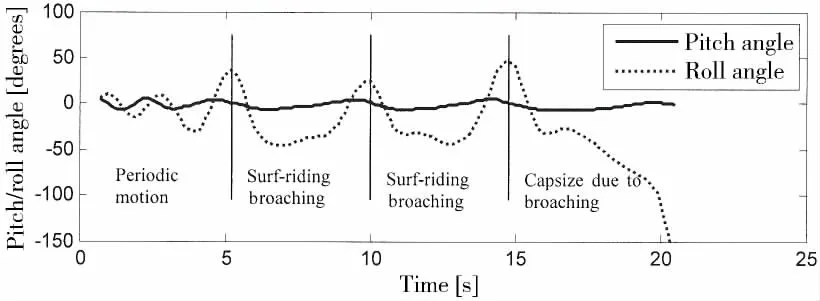
Fig.6 Time histories of pitch and roll angles(Fn=0.4,λ/L=1.25,H/λ=0.06,stern-quartering waves χ=30°)

Fig.7 Time histories of yaw and rudder angles(Fn=0.4,λ/L=1.25,H/λ=0.06,stern-quartering waves χ=30°)

Fig.8 Comparison of the results between calculation and model experiment(Fn=0.3)

Fig.9 Comparison of the results between calculation and model experiment(Fn=0.4)
In the experiment,the ship does not experience surf-riding at the cases with small steepness and wavelength to ship length ratio(Fn=0.3,λ/L=1.0,H/λ=0.05 and 0.08;Fn=0.4,λ/L=1.0,H/λ=0.08),which are inconsistent with the calculation results.It is because that the mathematical model of level 2 criterion is based on a single degree of freedom surge equation with the linear Froude-Krylov force,and could conservatively predict surf-riding for the unconventional ship in waves with small steepness and wavelength to ship length ratio.However,level 2 criterion is practical for its simple and conservative.For the ONR tumblehome vessel,which fails to pass level 2 criterion,the direct stability assessment using the advanced state-of-theart technology should be performed to avoid over conservative assessments.
3 Conclusions
Based on the sample calculation and the model experiment for surf-riding and broaching,the following conclusions can be summarized:
(1)The mathematical model of the current level 2 criterion is reasonable by analyzing the applicability of vulnerability criteria with the sample calculations.
(2)Four types of ship motions with periodic motion,stable surf-riding,broaching and capsizing due to broaching are observed in the experiment,while broaching is observed three times in one wave case.
(3)With the comparison of results between calculations and model experiment,level 2 criterion for surf-riding and broaching is also applicable to ONR tumblehome vessel.
This paper was presented at the 16th International Ship Stability Workshop,Belgrade Serbia,5-7 June 2017.
[1]IMO.Draft guidelines of direct stability assessment procedures for use with the second generation intact stability criteria[R].SDC 4/WP.4 Annex 1,2017.
[2]IMO.Amendments to part B of the 2008 IS Code on towing,lifting and anchor handling operations[R].SDC 3/WP.5,2016.
[3]IMO.Draft explanatory notes on the vulnerability of ships to the surf-riding/broaching stability failure mode[R].SDC 3/WP.5 Annex 5,2016.
[4]Kan M.A guideline to avoid the dangerous surf-riding[C].Proceedings of the 4th International Conference on Stability of Ships and Ocean Vehicles,1990:90-97.
[5]Spyrou K J.Asymmetric surging of ships in following seas and its repercussion for safety[J].Nonlinear Dynamics,2006,43:149-172.
[6]Maki A,Umeda N,Renilson M,Ueta T.Analytical formulae for predicting the surf-riding threshold for a ship in following seas[J].Journal of Marine Science and Technology,2010,15:218-229.
[7]Maki A,Umeda N,Renilson M,Ueta T.Analytical methods to predict the surf-riding threshold and the wave-blocking threshold in astern seas[J].Journal of Marine Science and Technology,2014,19:415-424.
[8]Umeda N,Hashimoto H.Qualitative aspects of nonlinear ship motions in following and quartering seas with high forward velocity[J].Journal of Marine Science and Technology,2002,6(2):111-121.
[9]Hashimoto H,Umeda N,Matsuda A.Importance of several nonlinear factors on broaching prediction[J].Journal of Marine Science and Technology,2004,9:80-93.
[10]Hashimoto H,Umeda N,Matsuda A.Model experiment on heel-induced hydrodynamic forces in waves for realizing quantitative prediction of broaching[J].Fluid Mechanics and Its Application,2011,96:379-398.
[11]Belenky V,Spyrou K,Weems K.Evaluation of the probability of surf-riding in irregular waves with the time-split method[C].Proceedings of the 11th International Conference on the Stability of Ships and Ocean Vehicles,2012:29-37.
[12]Spyrou K,Belenky V,Themelis N,Weems K.Conditions for surf-riding in an irregular seaway[C].Proceedings of the 11th International Conference on the Stability of Ships and Ocean Vehicles,2012:23-28.
[13]Belenky V,Weems K,Spyrou K.On Probability of surf-riding in irregular seas with a split-time formulation[J].Ocean Engineering,2016,120:264-273.
[14]Belenky V,Spyrou K,Weems K.On probability properties of surf-riding and broaching-to in irregular seas[C].31st Symposium on Naval Hydrodynamics,2016:264-273.
[15]IMO.Draft amendments to part B of the IS Code with regard to vulnerability criteria of levels 1 and 2 for the surf-riding/broaching failure mode[R].SDC 2/WP.4 Annex3,2015.
- 船舶力学的其它文章
- Numerical Study of the Shapes of the Super-Rogue Waves
- Hydroelasitic Analysis of the Gravity Cage Subjected to Irregular Waves and Current
- Application of Propagation Characteristics of Translating-Pulsating Source Green Function in the Side-Wall Effects Discrimination
- LES Simulations of the Flow Around a Propeller in Crash Back and Crash Ahead
- Investigations on the Mechanical Behavior of an Innovative Subsurface Tension Leg Platform in Ultra-Deep Water(Part I)
- Low-Cycle Fatigue Crack-Propagation Behavior of Ship Cracked Plate Considering the Accumulative Plasticity under Variable Amplitude Loading

