Numerical Study of the Shapes of the Super-Rogue Waves

LU Wen-yue,YANG Jian-min

(State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

0 Introduction

As an increasing number of accidents that occurred in recent years are believed to be associated with rogue waves,the physical mechanisms of this phenomenon have attracted much interest of researchers and offshore industry.Serious studies of the phenomenon started about 20-30 years ago and have intensified during the recent decade[1-5].One remarkable feature of the rogue waves is that they always appear from nowhere and quickly disappear without a trace.Thus,there is little useful at-sea evidence except for a limited number of visual sightings and a few photographic records.The study of the complex shapes of such extreme events becomes ultra-rear.As the nonlinear dynamics is one of the approaches to investigate the mechanisms of the formation of the rogue wave,the localised focusing of the wave energy is regarded as being the result of the modulational instability of uniformly traveling trains of Stokes waves in deep water.The modulational instability,which is also known as the Benjamin-Feir instability,has been extensively studied[6-8].The nonlinear process of the modulational instability of deep water waves is now widely accepted to be one of the main mechanisms to explain the generation of such extreme events.

The modulational instability was widely investigated based on the nonlinear Schrödinger(NLS)equation.The NLS equation was first derived by Zakharov[8]under the assumptions of being weakly nonlinear and spectrally narrowbandness,which is a relatively simple model that can be used to describe the evolution of the envelope of slowly modulated surface waves.Subsequently,the NLS equation was also derived by Mei[9]using a multiple-scale perturbation method.Then Dysthe[10]extended the envelope equation to include the fourth-order of ε(i.e.the wave steepness)by taking the perturbation expansion to the next order,obtaining the modified nonlinear Schrödinger equation(mNLS equation).Compared with the NLS equation,the mNLS equation retains the same spectral width constraint as the original NLS equation in O（ε）but accounts for the effects of several higher-order terms,such as nonlinear dispersion,first order dispersion of linear waves and the effect of wave induced current.Thus the mNLS equation can better describe the evolution of nonlinear waves than the NLS equation.

Fig.1 The profile of the first-order rational solution of the NLS equation.The maximum amplitude reaches the value of 3 times larger than the background carrier wave at the position X=0,T=0

One class of the NLS solutions have been regarded as being the prototype of a class of the rogue waves developing in a plane wave background[11-13].The whole hierarchy of rational solutions of the NLS equation can be constructed by using the modified Darboux Transformation[14].The first order rational solution is also known as the Peregrine breather which is identified with the limiting case of both the Ma solitons[15]and the Akhmediev breather[16]which is localized both temporally and spatially.It also describes the amplification of an initial infinitesimal disturbance of a plane wave and in which the maximum amplitude can reach three times of the initial wave amplitude.Fig.1 shows this solution,demonstrating clearly its spatial and temporal localization.It illustrates mathematically waves that can appear from nowhere and then disappear without a residual trace.At the position X=0,T=0,it generates a high amplitude rogue wave when the carrier wave reaches the peak value.

Higher-order rational breather solutions have also been reported as discussed in Refs.[14,16-19],which are localized both in time and space.They describe the superposition of the group of rogue waves and can result in waves that reach even higher amplitudes.Following the procedure mentioned above,higher-order rational solutions of the NLS equation can be constructed.Such waves have been usually named the super-rogue waves.The amplitude profiles of the national solutions from the 2nd order to 5th order are demonstrated in Fig.2.It was found[14]that the wave amplification described by different order rational solutions can reach 2j+1 times of the background waves,where j is the order of the rational solution.Additionally,the rational solutions of the NLS equation turn out to be reproducible in wave tank facilities[20-23].

Fig.2 The profile of the higher-order rational solutions of the NLS equation with the background amplitude q=1.The maximum amplitude of the jth order solution reaches the value of 2j+1 times larger than the background carrier wave at the position X=0,T=0

In this paper,the generation and evolution of 1st～5th order super-rogue waves were simulated numerically by solving the mNLS equation in order to investigate the shape of the super-rogue waves.The 4th order split-step pseudo-spectral method was used during the integral process in order to obtain more accurate results.Shapes of the super-rogue waves were analyzed by adoption of the conversion of coordinates and interpolation.

1 Mathematical model and numerical scheme

1.1 Mathematical model

In this section,the mNLS equation was used to simulate the generation and evolution of the super rogue waves numerically.

where B denotes the first harmonic of the complex velocity potential,is the mean velocity potential and the mean surface elevation due to radiation stress caused by the modulation of a finite amplitude wave,k and ω are the wave number and the wave frequency of the carrier wave respectively,cgis defined by cg=ω/2k as the group velocity and U denotes the current velocity.The complex conjugate is denoted by ‘*’.The velocity potential of the induced mean currentis governed by:

satisfying the boundary condition:

In order to compare the numerical results with the experimental measurements made in the associated follow-up study,it is more convenient to use the spatial version of mNLS.Thus we introduce the dimensionless variables similar to Lo and Mei in Ref.[24]:

where ε=ka and γ is a scale factor which renders the computational domain in ξ to 2π.With the primes omitted for brevity,the Eqs.(3)-(6)are redefined as follows:

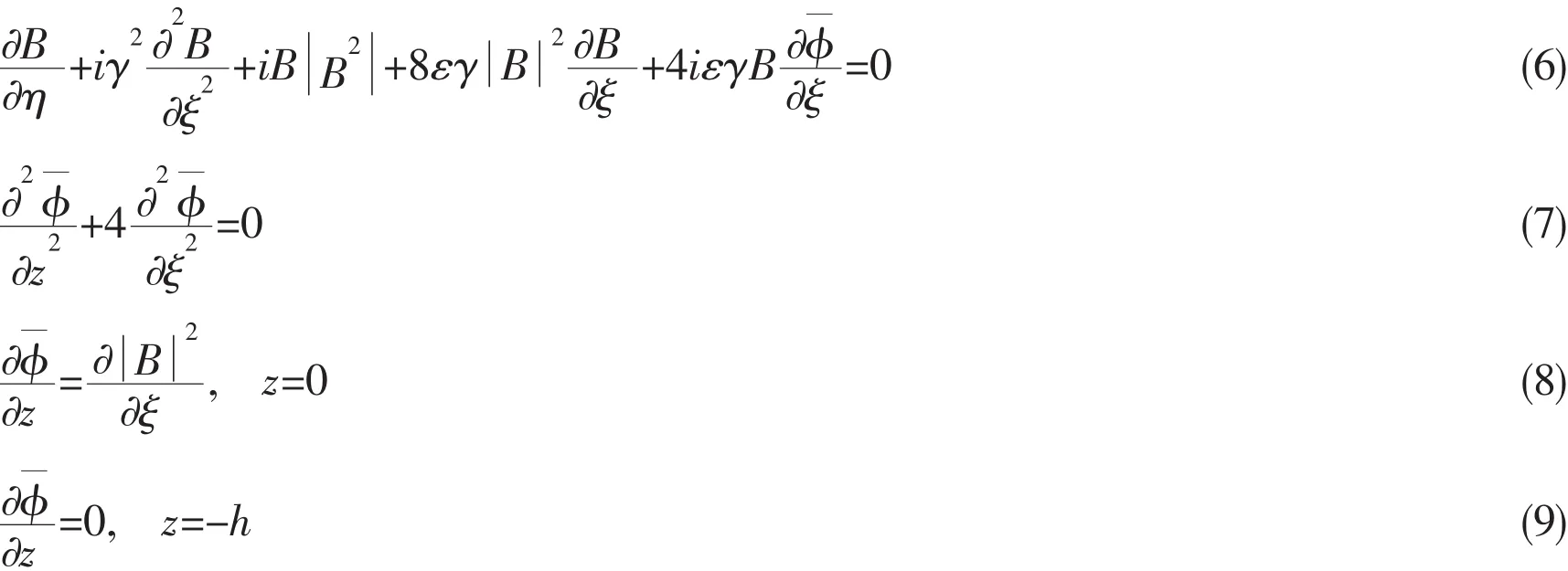
However,there is a significant point that has to be addressed when analyzing the surface elevation and the velocity potential.Noticeably,the amplitude B and the surface elevation ζ are different functions.Thus,the maximums of B and ζ may attain significantly different values.Then,the surface elevation is computed up to the third order of the bound waves.Namely,the wave surface elevation is obtained as follows:

where Ψ=-η/ε2+ξ/εγ is the phase function of the carrier waves.

1.2 Numerical scheme

The mNLS equations can be solved numerically by the split-step pseudo-spectral method[24],with a modification in which we used the fourth-order split-step method[25]and fourth-order Runge-Kutta method during the iteration processes of the linear part and nonlinear part respectively.The linear part and the nonlinear part of Eq.(8)are solved separately at each step.For the nonlinear part,we firstly solve the equation

In order to avoid the aliasing that can occur in numerical solutions,the rectangular window function is adopted during the Fast Fourier Transform.Since these higher order modes do not contribute to B,this does not change the overall solution.

In the numerical simulations,using the dimensionless variables the same as given in Eq.(11),we can obtain the ‘initial’condition of the super-rogue waves up to fifth order.65 536 grid points were used in a very large time interval corresponding to a sufficiently small value of parameter γ and the spatial integration step was set to be 3.75 cm which is considered to be sufficiently small in order to ensure the avoidance of numerical instabilities.In order to reconstruct the surface elevation from the solution of B and φ¯,65 536 grid points were used to represent the wave surface elevation.Thus,it is necessary to translate Eq.(12)to a discreteversion:

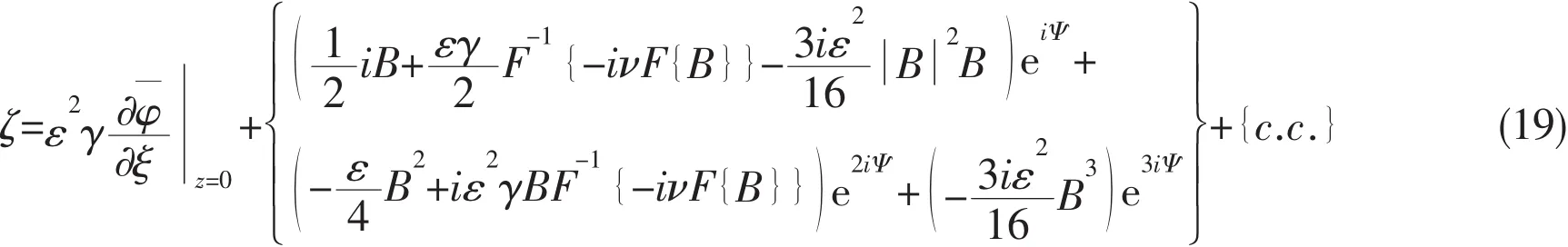
where ν=0,±1,±2,±3,…,±N/2 is Fourier mode.

Due to the occurrence of wave breaking during the amplification process of the wave amplitude for these rational solutions and the convenience for the comparison among the superrogue waves of the different orders,the choices for the parameters of the initial wave steepness were selected to be near the wave breaking condition of the 5th order rational solution based on the experiments cited in Refs.[20,23,26].Since the rational solutions of the NLS equation are defined on the infinite domain,the scale factor γ was set to be sufficiently small so that the time intervals can be much wider than the characteristic localization interval.Since the parameters used in numerical simulation is quite small,it needs very large spatial length for the 1st-5th order super-rogue waves to generate from small disturbance.The distance between the wave maker and the pre-arranged focusing point is 250 m and the total length of the numerical simulation is 300 m.The parameters that are used in the numerical simulations are given in Tab.1.

Tab.1 Parameters used for numerical simulations of first-to fifth-order rational solutions

2 Results and discussion

Taking the third-order super rogue wave as an example,the process of the generation and evolution of the third-order super rogue waves are demonstrated in Fig.3.The time history during the period of 500 seconds is illustrated at different positions.It is clearly shown that the third-order super rogue wave appears at the x=249.45 m with a very large amplitude.The initial disturbances under the background of a plane wave at the initial position absorb the wave energy around and then develop to the super rogue wave as the waves propagate forwards.It is also seen that the super rogue waves can be resulted in the nonlinear interaction between different wave groups.

Fig.3 Generation and evolution of the third-order super rogue wave

Fig.4 The spatial distributions of the 1st-5th order super-rogue waves

Fig.4 shows the spatial-distribution of the first-to fifth-order super rogue waves and the details of their shapes of the highest peaks.Deviation of the position where the super rogue waves appear from the pre-arranged position was observed in Fig.4.The higher order super rogue wave occurs at the earlier position due to the stronger effects of the nonlinear interaction between different wave groups.

Tab.2 Fitting results for the shapes of the first-to fifth-order super rogue waves

It is also found that the wave amplitudes around the super rogue waves are very small and the waves fluctuate widely near the location of the appearance of the super rogue waves.Strong asymmetry is observed in front of and behind the super rogue waves.Waves before the appearance of the super rogue waves are gentle while the areas of waves after that become rough which coincides with suddenness and unpredictability of rogue wave.The shapes of the first-to fifth-order super rogue waves are analysed by adopting the curve fitting as shown in Fig.4.The fitting function is chose to be the standard sine function and the fitting results are summarised in Tab.2.Asymmetries are also observed during the appearance of the super rogue wave between the peaks and troughs.As the order of the super rogue wave grows,the deviation of the shapes between the super rogue wave and the sinusoidal wave becomes more obvious,namely,the peak increases while trough decreases.It can also clearly notice that the wave number of the single super rogue wave becomes larger as its order grows,which means its wave length decreases leading to the stronger nonlinear interaction during the evolution.

3 Conclusions

In this study,the first-to fifth-order super rogue wave events were simulated numerically by solving the mNLS equation.The generation and evolution of the first-to fifth-order rational solutions of the NLS equation were investigated which had been observed in the wave tank.To overcome the limit of the physical length of the test facility and the layout of measurement gauges,these super rogue waves were simulated numerically in order to investigate the spatial-distribution of the super rogue waves and the property of their wave shapes.

The position where the super rogue waves appear are different from that expected by their analytical solutions due to the higher-order nonlinear effects.Thus,the fourth-order nonlinear terms in the mNLS equation cannot be ignored during numerical simulation.

Asymmetries are observed in the area in front of and behind the appearance of the super rogue wave which coincides with suddenness and unpredictability of rogue wave.The asymmetries between the peak and trough also show the deviation of the shapes between the super rogue wave and the sinusoidal wave becomes more obvious duo to the increase of the nonlinearity as the order of the super rogue wave grows.

Acknowledgement

This work was financially supported by the National Natural Science Foundation of China(Grant No.51239007).The authors would also like to acknowledge the support of the Sino-UK Higher Education Research Partnership for PhD Studies funded by the British Council in China and the China Scholarship Council.

Nomenclature

[1]Adcock T A A,Taylor P H.The physics of anomalous(‘rogue’)ocean waves[J].Rep.Prog.Phys.,2014,77(10):105901.

[2]Onorato M,Residori S,Bortolozzo U,Montina A,Arecchi F T.Rogue waves and their generating mechanisms in different physical contexts[J].Physics Reports,2013,528(2):47-89.

[3]Slunyaev A,Didenkulova I,Pelinovsky E.Rogue waters[J].Contemp Phys.,2011,52(6):571-590.

[4]Dysthe K,Krogstad H E,Müller P.Oceanic rogue waves[J].Annual Review of Fluid Mechanics,Davis,and Moin,eds.,2008:287-310.

[5]Kharif C,Pelinovsky E.Physical mechanisms of the rogue wave phenomenon[J].European Journal of Mechanics,B/Fluids,2003,22(6):603-634.

[6]Onorato M,Osborne A R,Serio M,Cavaleri L,et al.Extreme waves,modulational instability and second order theory:Wave flume experiments on irregular waves[J].European Journal of Mechanics,B/Fluids,2006,25(5):586-601.

[7]Onorato M,Osborne A R,Serio M,Bertone S.Freak waves in random oceanic sea states[J].Phys Rev Lett,2001,86(25):5831-5834.

[8]Zakharov V E.Stability of periodic waves of finite amplitude on the surface of a deep fluid[J].J Appl Mech Tech Phys,1968,9(2):190-194.

[9]Mei C C.The applied dynamics of ocean surface waves[J].World Scientific,Singapore,1989.

[10]Dysthe K B.Note on a modification to the nonlinear Schrödinger equation for application to deep water waves[J].Proceedings of the Royal Society of London.Mathematical and Physical Sciences,1979,369(1736):105-114.

[11]Shemer L,Alperovich L.Peregrine breather revisited[J].Physics of Fluids,2013,25(5):287-433.

[12]Shrira V I,Geogjaev V V.What makes the Peregrine soliton so special as a prototype of freak waves?[J].J Eng.Math.,2010,67(1):11-22.

[13]Peregrine D.Water waves,nonlinear Schrödinger equations and their solutions[J].The Journal of the Australian Mathematical Society,Series B,Applied Mathematics,1983,25(01):16-43.

[14]Akhmediev N,Ankiewicz A,Soto-Crespo J M.Rogue waves and rational solutions of the nonlinear Schrödinger equation[J].Phys.Rev.E Stat.Nonlinear Soft Matter Phys.,2009,80(2):026601.

[15]Ma Y C.Perturbed plane-wave solutions of the cubic Schrödinger equation[J].Stud.Appl.Math.,1979,60(1):43-58.

[16]Akhmediev N,Eleonskii V,Kulagin N.Exact first-order solutions of the nonlinear Schrödinger equation[J].Theoretical and Mathematical Physics,1987,72(2):809-818.

[17]Gaillard P.Wronskian representation of solutions of the NLS equation and higher Peregrine breathers[J].Scientific Advances,2012,13(2):71-153.

[18]Dubard P,Gaillard P,Klein C,Matveev V B.On multi-rogue wave solutions of the NLS equation and positon solutions of the KdV equation[J].Eur.Phys.J:Spec.Top.,2010,185(1):247-258.

[19]Akhmediev N,Ankiewicz A,Taki M.Waves that appear from nowhere and disappear without a trace[J].Phys Lett Sect A Gen At Solid State Phys,2009,373(6):675-678.

[20]Chabchoub A,Hoffmann N P,Akhmediev N.Observation of rogue wave holes in a water wave tank[J].J Geophys.Res.-Oceans,2012,117:5.

[21]Chabchoub A,Hoffmann N,Onorato M,Slunyaev A,Sergeeva A,Pelinovsky E,Akhmediev N.Observation of a hierarchy of up to fifth-order rogue waves in a water tank[J].Phys.Rev.E,2012,86(5):6.

[22]Chabchoub A,Hoffmann N,Onorato M,Akhmediev N.Super roguewaves:Observation of a higher-order breather in waterwaves[J].Phys.Rev.X,2012,2(1).

[23]Chabchoub A,Hoffmann N P,Akhmediev N.Rogue wave observation in a water wave tank[J].Phys Rev Lett,2011,106(20):204502.

[24]Lo E,Mei C C.Numerical study of water-wave modulation based on a higher-order nonlinear Schrödinger equation[J].Journal of Fluid Mechanics,1985,150:395-416.

[25]Muslu G M,Erbay H A.Higher-order split-step Fourier schemes for the generalized nonlinear Schrödinger equation[J].Math Comput Simul,2005,67(6):581-595.

[26]Slunyaev A,Pelinovsky E,Sergeeva A,Chabchoub A,Hoffmann N,Onorato M,Akhmediev N.Super-rogue waves in simulations based on weakly nonlinear and fully nonlinear hydrodynamic equations[J].Phys.Rev.E Stat.Nonlinear Soft Matter Phys.,2013,88(1):012909.