基于风险的非一致性设计洪水及其不确定性研究
杜 涛,熊立华,李 帅,邵 骏,许崇育,4,闫 磊
(1.长江水利委员会水文局,湖北 武汉 430010;2.武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072;3.中国长江三峡集团有限公司,湖北 宜昌 443133;4.奥斯陆大学 地学系,挪威 奥斯陆 N-0316)
1 研究背景
设计洪水是水利工程规划设计、防洪决策等工作的一个重要特征值[1-2]。由于气候变化及人类活动影响,水文极值事件存在非一致性已成为共识[3-6],致使基于一致性假设所得的设计结果受到质疑。因此,研究非一致性条件下设计洪水具有重要的实际应用价值。
目前,关于水文极值序列非一致性的研究主要集中于时变矩法[7-8],其基本思想是:假设水文变量所服从的分布类型不变,但分布的统计参数随时间或其他气象协变量变化。在此情况下,给定某一超过概率p,不难得出每年各自的设计值,即,其中为水文极值变量Z的逆分布函数,θt为第t年的统计参数向量。Strupczewski等[9-11]首次提出一个非一致性洪水频率分析模型,将趋势性成分引入到洪水频率分布的一、二阶矩中;Katz等[12]在前人基础上直接建立了洪水频率分布参数与时间的关系;Villarini等[13]基于考虑位置、尺度和形状的广义可加模型(Generalized additive Models for Location,Scale and Shape, GAMLSS)研究了Little Sugar Creek流域年最大洪水趋势性变化问题,结果发现传统意义下100年一遇的设计洪水在非一致性条件下已不再是一个固定值,该设计值最小为1957年的2.1 m3s-1km-2,最大为2007年的5.1 m3s-1km-2。理论上,时变矩方法能够较好地描述洪水极值序列年际间的非一致性变化情况,然而在实际应用中,给定某一超过概率,每年都有一个设计值较难应用于实际[14]。Schumann[15]指出,考虑水文风险的水文极值事件设计值对水利工程规划设计显得越发重要。梁忠民等[16]基于“等可靠度”的概念建立了一致/非一致性条件下设计洪水计算方法间的联系,保证了非一致性条件下水文设计成果与现行工程采用的成果之间的衔接与协调。Rootzén等[17]将水文风险概念引入到非一致性极值事件设计值的研究中。他们指出,在变化环境下水利工程规划设计中,应该量化两方面的基础信息:①设计使用年限,即水利工程将发挥作用的年限;②水文风险,即设计使用年限内水文极值事件超过某一特定设计值的概率。在给定设计使用年限及水文风险情况下,将有唯一的设计值与之对应,称之为基于风险的水文极值事件设计值。Rootzén等[17]应用以上方法研究了变化环境下非一致性年最大日降水及年最低气温的设计值。该方法为非一致性极值事件设计值的研究提供了一种基于风险的新思路,但其中存在有待改进之处,即在应用时变矩法对非一致性极值序列进行频率分析时仅选取时间因子作为协变量。单纯以时间为协变量既无法拟合统计参数波动性变化较为复杂的情况,同时又缺乏物理意义,更重要的是进一步推求设计使用年限内极值事件的统计分布时,假设所拟合出的上升、下降趋势或者跳跃突变将在未来时期无限延续下去。
综上,有研究选取具有物理意义的气象因子为协变量进行非一致性水文频率分析[7-8],同时也有研究以时间为协变量,将水文风险概念引入到非一致性极值事件设计值推求当中[17],但未见有研究将两者相结合,以推求更具物理意义的非一致性设计洪水成果。本文拟采用该方法探讨变化环境下渭河流域洪水极值事件的设计值,并用自助抽样(Bootstrap)方法[18]推求该设计值的不确定性,以期为水利工程规划设计及防洪决策提供一定参考依据。
2 研究区域及数据
渭河发源于甘肃省渭源县鸟鼠山,是黄河最大支流。干流总长818 km,流域面积134 800 km2,界于黄土高原东南部 33°40′—37°26′N,103°57′—110°27′E之间(图 1)。渭河流域地处半干旱半湿润的大陆性季风气候区,多年平均降水量540 mm(1954—2009年,下同),年平均气温6~14℃,年潜在蒸散发量660~1600 mm,多年平均天然径流量100亿m3,约占黄河的17%[19-20]。
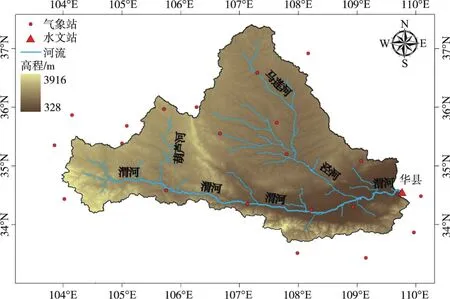
图1 渭河流域水系及水文气象站点
本研究主要应用3类数据:(1)观测水文数据;(2)观测气象数据;(3)美国国家环境预报中心(National Centres for Environmental Prediction,NCEP)再分析数据以及国际耦合模式比较计划第5阶段(Coupled Model Intercomparison Project Phase 5, CMIP5)提供的大气环流模型(General Circulation Mod⁃el,GCM)输出数据。
(1)华县水文站1954—2009年日平均流量数据来自黄委水文局,选取其年最大日平均流量序列作为洪水极值事件进行研究(图2(a))。华县站位于渭河与黄河接口上游70 km处,站点控制面积106 500 km2,约为渭河流域总面积的80%。
(2)气温和降水是与径流密切相关的气象变量,因此本研究选取其作为协变量对洪水序列进行非一致性频率分析。渭河流域及其周边22个气象站点1954—2009年日平均气温及日总降水来自中国气象科学数据共享网(http://cdc.cma.gov.cn)。两个变量的面平均序列由泰森多边形法获得,进一步提取年平均气温(Temp)及年总降水(Prep)统计量作为非一致性洪水频率分析的协变量(图2(b)(c))。理论上讲,季节性气象统计量应更适合于描述洪水极值事件的非一致性,考虑到华县站约有90%的实测洪水极值事件发生在7—10月,本研究同样检验了夏季平均气温(TempS)和夏季总降水(PrepS)与实测洪水序列的相关性(图2(d)(e)),结果稍低于年值统计量。
(3)本文应用NCEP再分析数据及CMIP5提供的GCM输出数据结合统计降尺度方法[21]获取气温及降水的未来情景。1954—2009年的NCEP预报因子来自NOAA地球系统研究实验室(ESRL)(http://www.esrl.noaa.gov)[22-23]。GCM输出数据选取IPCC第5次评估报告中RCP2.6、RCP4.5和RCP8.5三种排放情景下 9个模型(BCC-CSM1.1,BNU-ESM,CanESM2,CCSM4,CNRM-CM5,GFDL-ESM3M,HadGEM2-ES,MIROC-ESM-CHEM,NorESM1-M)2010—2099年与NCEP相应的大尺度预报因子(http://cmip-pcmdi.llnl.gov/cmip5)。由于NCEP和GCM数据均为网格数据且空间分辨率不同,本研究首先将两组数据插值到气象站点,再应用泰森多边形法获取各预报因子的流域面平均序列。
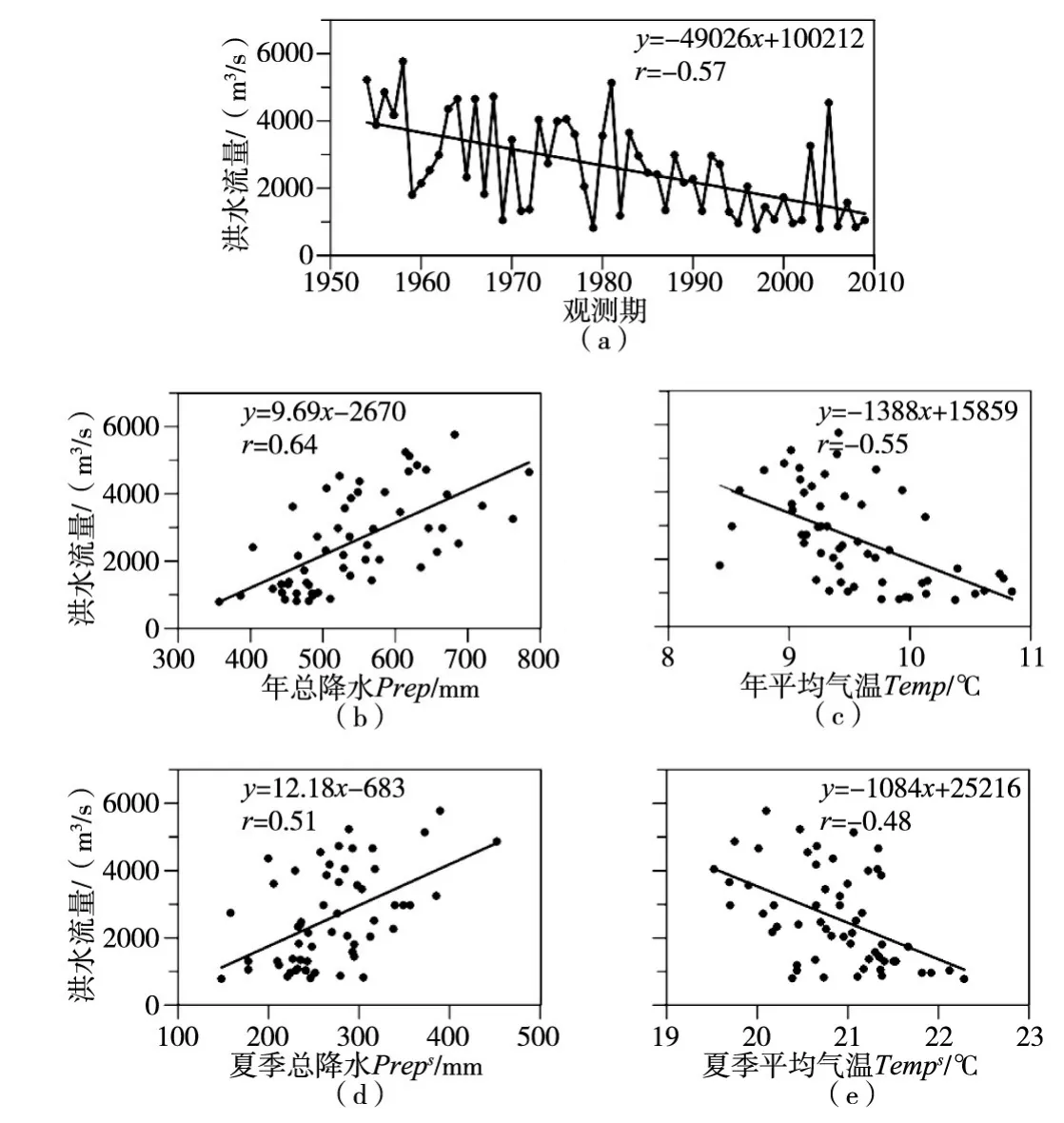
图2 华县水文站实测洪水序列与气象协变量相关关系
3 研究方法
3.1 水文风险及设计洪水量级随机变量Z表示洪水极值事件。在一致性条件下,FZ(z,θ0)表示Z的累积概率分布函数,其中θ0为固定的统计参数向量。给定某一特定设计使用年限T,则该设计使用年限内洪水极值事件超过某一设计值zT的概率,即一致性条件下zT所对应的水文风险RT为[14,17]:
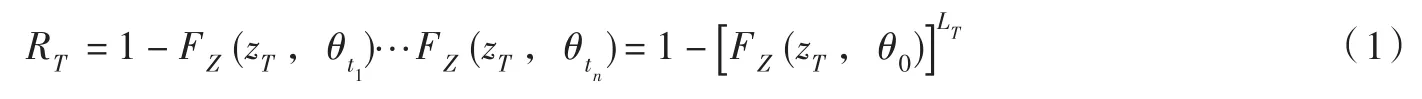
式中:LT为设计使用年限总年数;t1和tn分别为设计使用年限初年和末年。
此时,给定某一水文风险RT,可推求相应的一致性设计洪水量级zT,即转变式(1)为:

在非一致性条件下,FZ(z,θt)表示Z的累积概率分布函数,其中统计参数向量θt随时间或其他物理因子变化。于是有非一致性情况下设计值zT所对应的水文风险为:
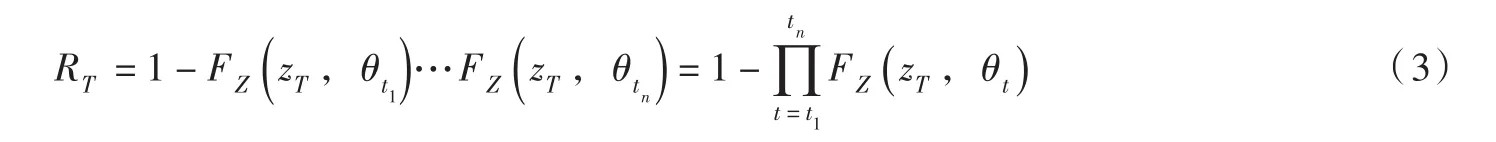
此时,给定某一水文风险RT,相应的非一致性设计洪水量级zT将无法像式(2)显式表达,但可通过数值迭代求出其数值解。当θt=θ0,即一致性条件仍成立,式(3)将退化为式(1)。
通过对实测洪水序列进行非一致性频率分析,进一步求出式(3)中设计使用年限内各年的统计参数θt。此时针对特定设计使用年限T可进行两方面研究:①对于某一量级的设计洪水zT,推求非一致性条件下的水文风险RT;②对于某一水文风险RT,推求非一致性条件下相应的设计洪水量级zT。第①种情况易于求解,然而实际工程设计中通常更关心第②种情况的设计结果,因此本文将对给定水文风险条件下的非一致性设计洪水及其不确定性进行研究。
3.2 非一致性洪水频率分析针对特定设计使用年限T及相应风险RT,研究非一致性设计洪水量级zT的一个重要步骤即确定式(3)中设计使用年限内各年的统计参数θt,而θt的确定又依赖于其与协变量之间的函数关系,即非一致性洪水频率分析。本文前述国内外相关研究成果中通常仅选取时间因子为协变量进行非一致性频率分析并进一步推求极值事件的设计值[14,17],而气象变量相比于时间具有更强的物理意义及解释能力,因此本文将建立洪水概率分布统计参数与气象因子的关系,并结合统计降尺度下GCM输出的气象数据获得设计使用年限内各年的统计参数θt,最终推求某一水文风险RT所对应的非一致性设计洪水量级zT及其不确定性。本文同时选取了以时间为协变量的情况进行比较研究。选取国内外较为常用的两参数Gumbel(GU)分布和三参数GEV分布、P-Ⅲ分布作为备选洪水频率分布,详见表1。由于GEV和P-Ⅲ分布的形状参数非常敏感且较难估计,通常不考虑该参数的非一致性变化[12,24-26],故本文同时检查各备选分布位置参数μ及尺度参数σ的非一致性[27],并应用赤池信息准则(Akaike Information Criterion, AIC)评价准则[28]选取最优非一致性模型。用worm图[29]、分位图、Filliben相关系数(Fr)[30]以及 Kolmogorov-Smirnov(KS)检验统计量(DKS)[31]评价模型拟合优度。

表1 非一致性洪水频率分析备选概率分布
3.3 统计降尺度模型(SDSM)GCM输出数据使得预估未来时期气象因子成为可能,将其引入以气象因子为协变量的最优非一致性模型中便可获取设计使用年限T内各年的统计参数θt并进一步计算与水文风险RT相应的设计洪水量级zT。然而,较低的空间分辨率限制了GCM的应用范围,针对此问题,Wilby等[21,32]提出了统计降尺度模型(SDSM)来建立大尺度预报因子与区域或站点尺度预报量间的关系,该模型融合了天气发生器和多元线性回归技术。本文应用SDSM结合站点实测气象数据、NCEP及GCM数据对渭河流域的气温和降水进行降尺度。
综上,本文基于风险的非一致性设计洪水及其不确定性研究流程如图3所示。
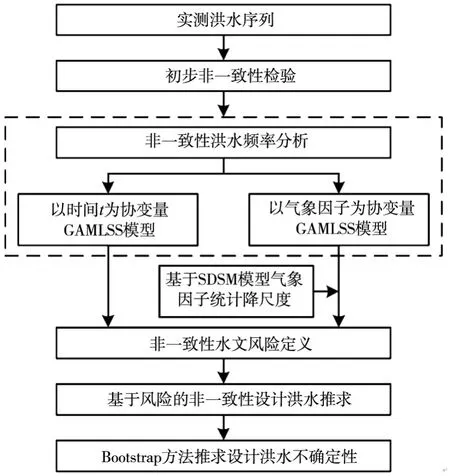
图3 基于风险的非一致性设计洪水及其不确定性研究流程
3.4 Bootstrap方法推求设计洪水不确定性本研究采用Bootstrap方法[18]推求由于样本数据长度有限所引起的设计洪水统计不确定性。
(1)一致性条件下,采用Bootstrap方法计算设计洪水不确定性具体步骤为:①由原始实测洪水序列计算一定水文风险RT下的设计洪水量级zT;②采用有放回方式从原始实测洪水序列中抽取与其等长度的新样本序列;③用新样本序列重新计算风险RT下的设计洪水量级;④重复第②、③步N次,得到N个抽样设计值,i=1,2,…,N ;⑤对N个抽样设计值由小到大排序,zT的置信区间为。
(2)非一致性条件下,无法从原始样本中直接抽样,需要采用对一致性残差进行抽样的方法来推求设计值的不确定性,具体步骤为:①由原始实测洪水序列计算一定水文风险RT下的设计洪水量级zT;②由非一致性洪水频率分析得到的时变统计参数计算模型标准正态残差③采用有放回方式从残差序列ri,i=1,2,…,n中抽取与其等长度的新残差序列;④用新残差序列计算洪水样本序列,重新按照第①步计算风险RT下的设计洪水量级;⑤重复第③、④步N次,得到N个抽样设计值;⑥对 N个抽样设计值由小到大排序,zT的100(1-α)%置信区间为。
4 实例分析
4.1 洪水序列非一致性识别及模型建立采用Mann-Kendall检验法对实测洪水序列进行初步非一致性检验,结果表明序列存在明显下降趋势。GAMLSS模型拟合结果如图4所示,结果表明,一致性情况下的最优分布为P-Ⅲ分布;以时间t为协变量情况下的最优分布同样为P-Ⅲ分布,且位置参数为时间的线性函数为最优非一致性模型。定性评价指标(worm图和分位图)表明模型能够通过显著性水平为0.05的拟合优度检验(图5(c)(d)),定量评价指标同样说明选取的最优非一致性模型能够通过检验(表2),然而如前文所述,以缺乏物理意义的时间因子为协变量,不能对洪水序列的波动性给出较好的拟合(图5(d))。
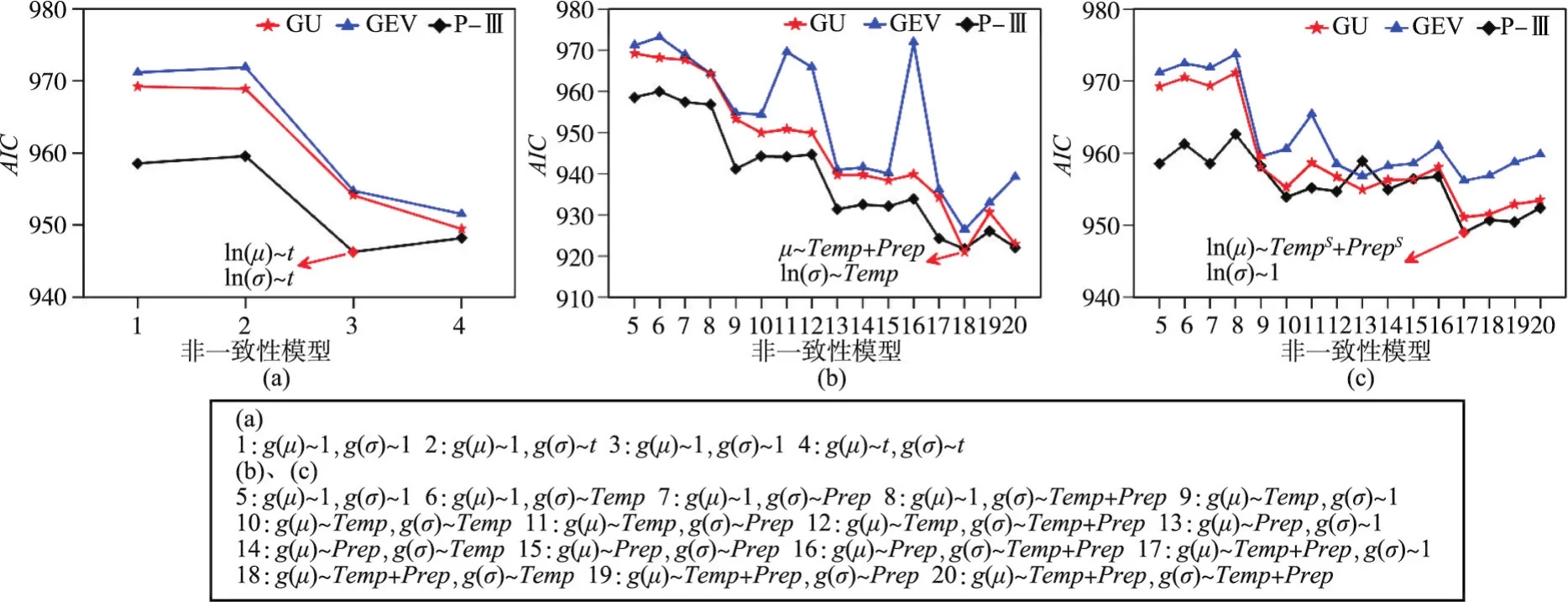
图4 非一致性模型拟合结果比较
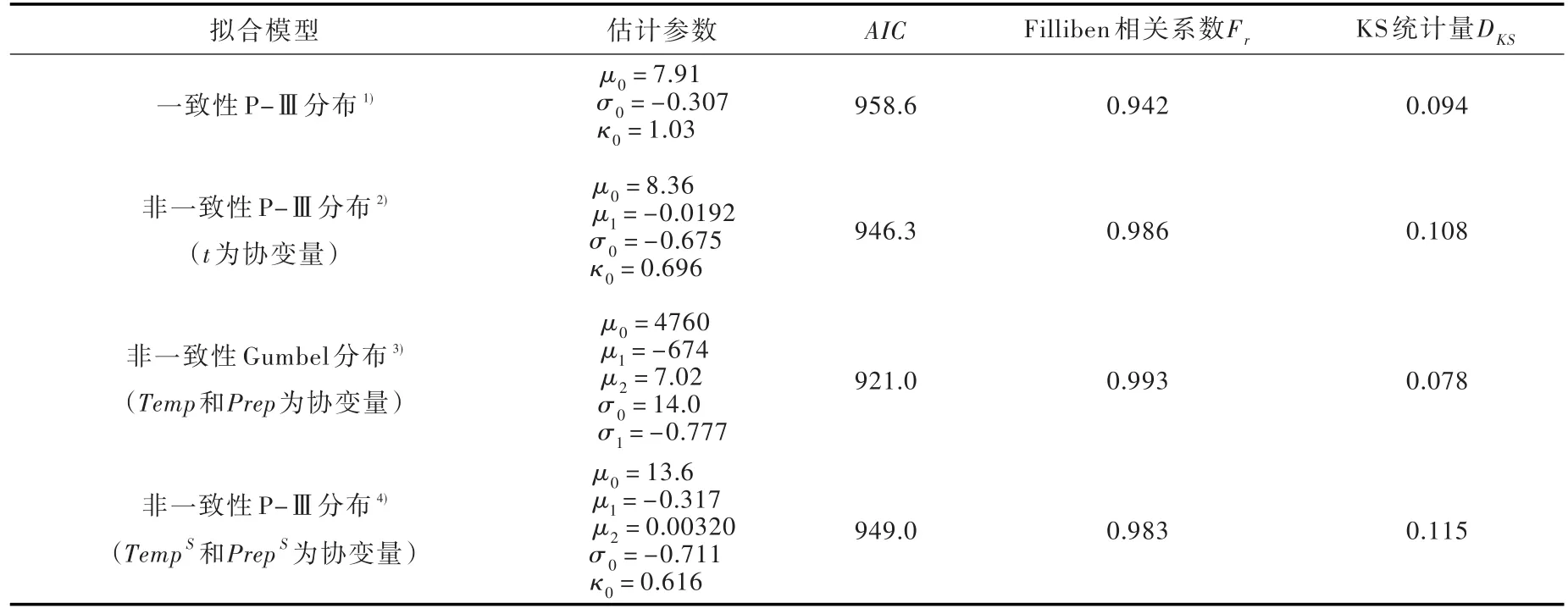
表2 渭河流域实测洪水序列非一致性频率分析结果及评价指标统计量
以年平均气温Temp及年总降水Prep为协变量对实测洪水序列进行频率分析时,AIC评价准则表明Gumbel分布为最优分布,且μ和σ两个统计参数分别为Temp、Prep以及Temp的线性函数为最优非一致性模型。定性和定量评价结果同样说明所选取的最优非一致性模型能够通过拟合优度检验(图5(e)(f)和表2)。而且,以Temp和Prep为协变量的最优模型相比于以t为协变量具有更小的AIC值,同时其不仅能够拟合出洪水序列的下降趋势,还可以对其波动性给出较好的拟合(图5(f)),进一步印证了选取具有物理意义的气象因子作为协变量的必要性和有效性。本研究同样分析了以季节性统计量为协变量的情况,结果表明,P-Ⅲ分布为最优分布,且μ为TempS、PrepS的线性函数,σ和κ均为常数,相应模型检验结果见表2,最终发现该最优非一致性模型效果远差于以Temp和Prep为协变量情况,甚至不及以时间t为协变量情况。
本文同样给出了一致性情况下拟合优度检验结果,结果表明,模型的Filliben相关系数不能通过显著性检验,说明渭河流域实测洪水序列确实存在显著的非一致性,若仍然以一致性假设为前提进行工程规划设计将增大事故风险。
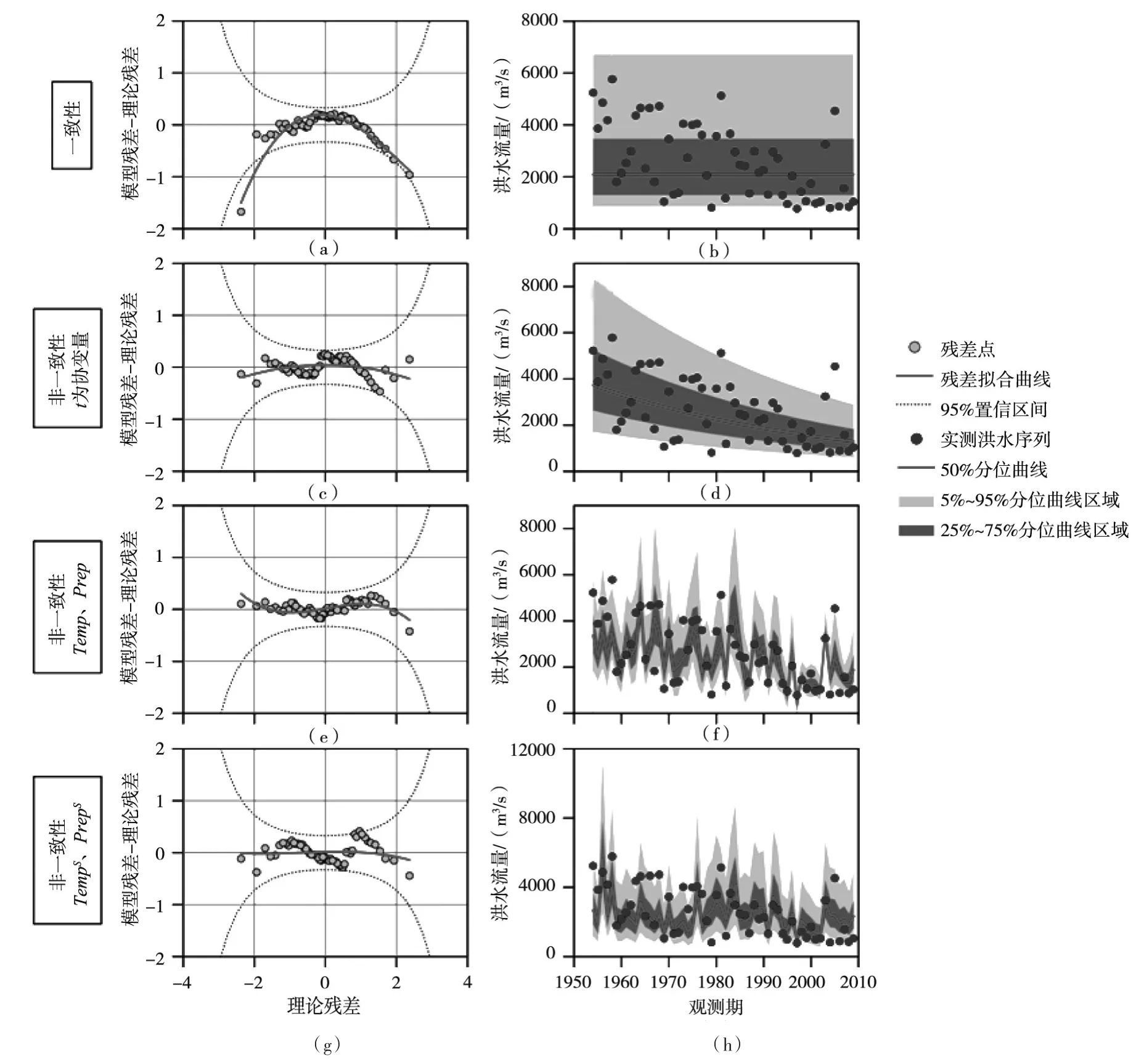
图5 渭河流域最优非一致性模型拟合优度检验worm图及分位曲线图
依据最优分布线型及参数变化情况,用1954—2000年资料重新拟合每种情况下的最优非一致性模型,进而将所得模型应用于2001—2009年以验证模型效果,结果见图6。结果表明,相比一致性模型和以时间t为协变量的非一致性模型,以气象因子为协变量的非一致性模型具有更强的预测能力。
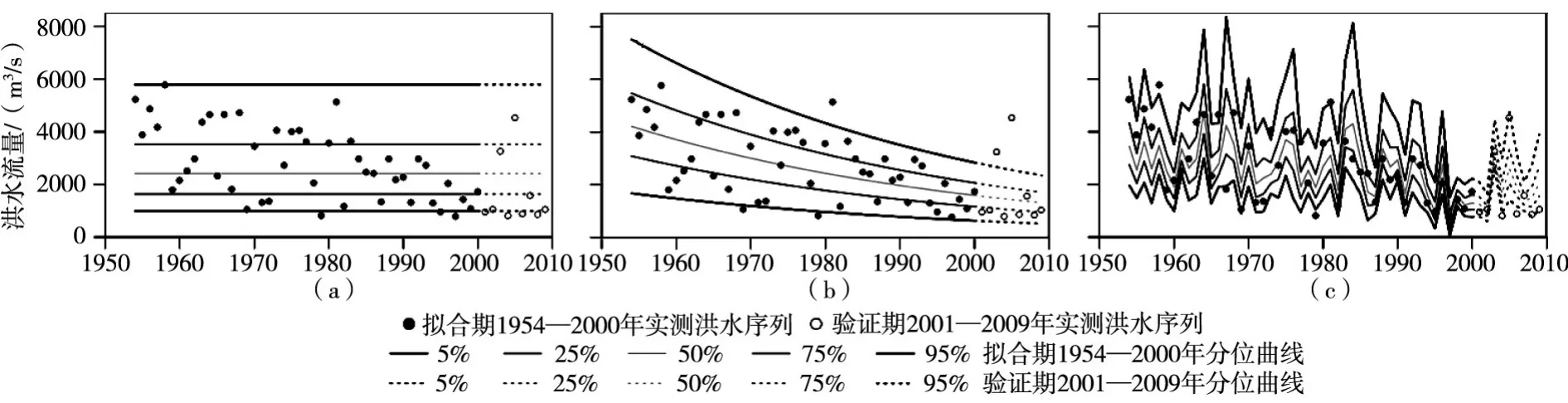
图6 最优洪水频率分布模型验证
4.2 降水及气温的统计降尺度对于以气象因子为协变量的最优非一致性模型,需要提供协变量未来年份的预估值才能进一步计算设计使用年限T内各年的统计参数μt和σt以及特定水文风险RT下的非一致性设计洪水zT。参考Wilby等[21,32],经相关性分析,本文最终选取降水和气温的预报因子如表3所示。

表3 日降水和日平均气温降尺度所选大尺度预报因子及模型类型
本文实测日降水和日平均气温为1954—2009年共56年资料,在建立SDSM模型时,选取1954—1993年共40年的数据率定模型,1994—2009年共16年的数据验证模型。结果表明,所建立的SDSM模型在率定期和检验期内模拟值与观测值拟合良好,结果见图7。进一步将3个典型浓度路径(RCP2.6、RCP4.5和RCP8.5)下的9个GCM模式[33]输出的大尺度气候因子2010—2099年的未来预估值代入到所建立的SDSM模型当中,生成每个GCM模式下2010—2099年日降水和日平均气温的未来预估值,进一步统计渭河流域年总降水和年平均气温未来时期各模型预估结果如图8所示。
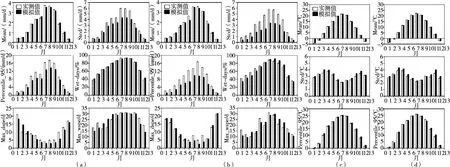
图7 渭河流域日降水((a)、(b))和日平均气温((c)、(d))SDSM模型模拟结果((a)、(c)率定期,(b)、(d)检验期)
为减小GCM模式选取的差异性,采用每个典型浓度路径下多模型平均值推求非一致性设计洪水[34]。RCP2.6、RCP4.5和RCP8.5三种典型浓度路径下多模型平均序列及其趋势线如图9所示。对于年总降水,每个RCP下差别并不大,随着辐射强迫的增强,序列逐渐由轻微下降转变为轻微上升,但幅度都较小(图9(a));对于年平均气温,每个RCP下都呈现出一定的上升趋势,随着辐射强迫的增加,上升越显著,RCP2.6情景下年平均气温首先有较为缓慢的上升,到2040年左右趋于稳定;RCP4.5情景下2070年以前上升较为明显,之后趋于稳定;在最高辐射强迫的RCP8.5情景下,呈现出明显的直线上升趋势(图9(b))。
4.3 非一致性设计洪水推求本文选取设计使用年限T为2015—2064年的50年。以时间为协变量时,设计使用年限t=2015,2016,…,2064年内时变统计参数μt和σt可由最优非一致性模型(表2)直接计算。给定水文风险R2015-2064,进而迭代推求相应的非一致性设计洪水z2015-2064。以Temp和Prep为协变量时,将设计使用年限t=2015,2016,…,2064年内Temp和Prep的降尺度数据(多模型平均值)代入最优非一致性模型(表2)计算时变统计参数μt和σt,进而推求与R2015-2064相应的非一致性设计洪水z2015-2064。同时给出了一致性假设成立情况下不同水文风险对应的设计洪水。
结果表明,以气象因子Temp和Prep为协变量时,3种典型浓度路径下非一致性设计洪水差别很小,随着辐射强迫的增加,设计洪水有轻微的增大,但并不显著,因此下面仅以RCP2.6情景下设计结果为代表进行分析。无论以时间t或者Temp和Prep为协变量,所得的非一致性设计洪水均明显偏低于一致性假设情况。意味着在考虑非一致性的情况下,设计使用年限内洪水极值事件相比于一致性假设将明显减弱,从观测期的洪水序列也发现明显的下降趋势(图2(a)),说明考虑非一致性的设计结果较为合理。
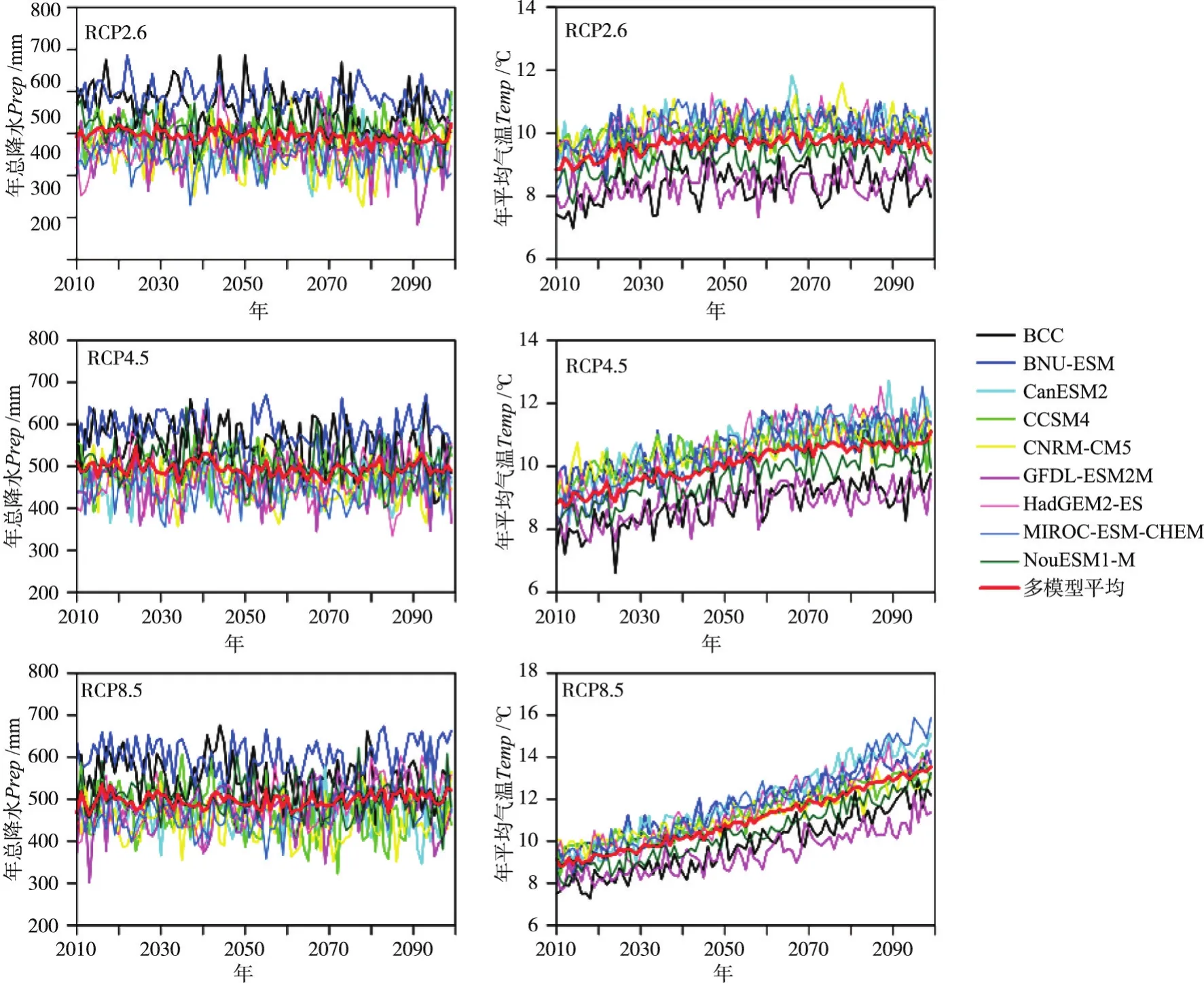
图8 渭河流域RCP2.6、RCP4.5和RCP8.5三种典型浓度路径下9个GCM模式[33](左)年总降水和(右)年平均气温未来时期(2010—2099年)预估值
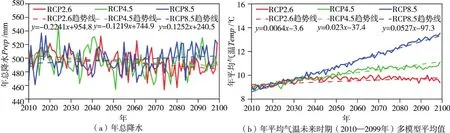
图9 渭河流域RCP2.6、RCP4.5和RCP8.5三种典型浓度路径下9个GCM模式年总降水和年平均气温未来时期(2010—2099年)多模型平均值
同时,两种非一致性设计结果间也存在较大差别,以t为协变量的设计结果明显偏低于以Temp和Prep为协变量的情况。虽然观测期的洪水序列表明渭河流域的洪水极值事件确实存在一定的减弱趋势,然而由于时间协变量情况假设所拟合出的下降趋势将在未来时期延续下去,基于此外延假设得到的设计洪水不免有些夸张。
当R2015-2064=10%,以t为协变量的非一致性设计洪水量级为3303 m3/s,意味着在未来2015—2064的50年间,超过3303 m3/s的洪水极值事件发生概率为10%,然而在观测期1954—2009的56年间,此事件却发生18次,说明以t为协变量的设计结果减弱趋势确实有所偏大,若以该设计结果为依据可能会增加工程事故风险。相比之下以Temp和Prep为协变量的设计结果6126 m3/s显得更为合理。应该指出,在假设一致性条件仍成立情况下,该设计值达到13 168 m3/s,而观测期内最大洪水量级也仅为5770 m3/s,更加印证了一致性设计结果的不合理性。
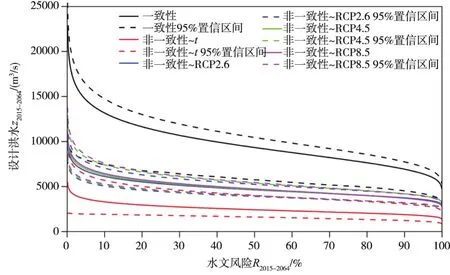
图10 不同水文风险R2015-2064对应的设计洪水z2015-2064及其95%置信区间
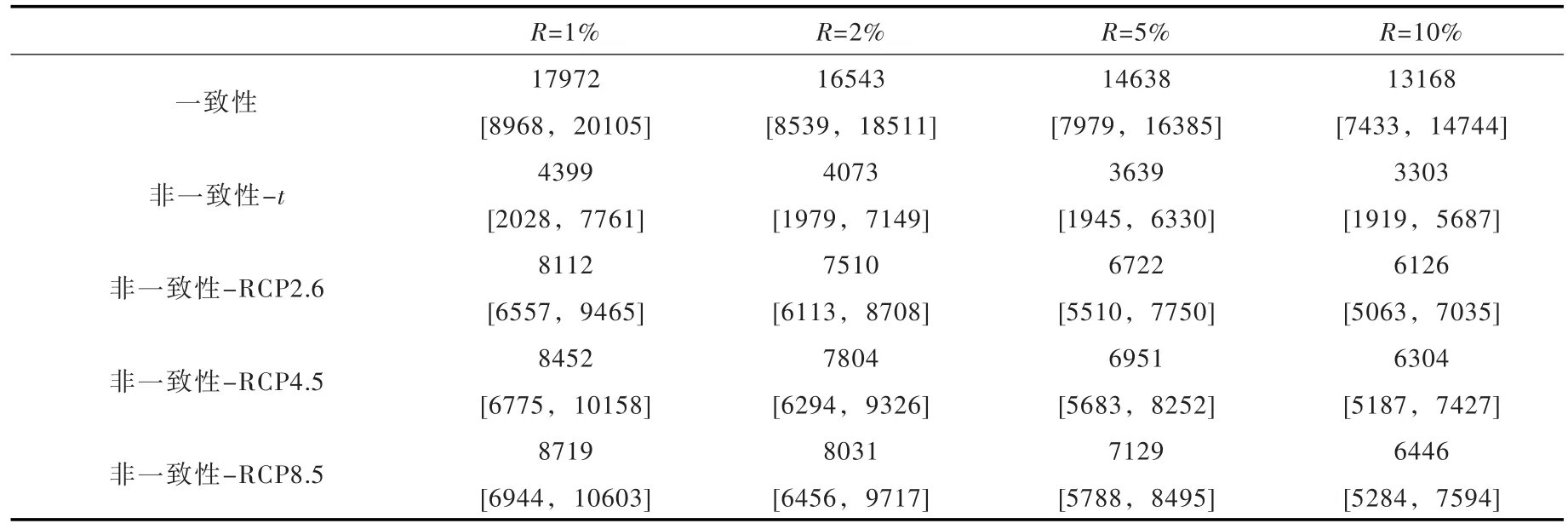
表4 设计洪水结果统计 (单位:m3/s)
4.4 非一致性设计洪水不确定性采用Bootstrap方法推求设计洪水不确定性,抽样结果见图11,相应的95%置信区间见图10及表4。通过对华县站进行历史大洪水调查,1933年历史洪水量级8340 m3/s,从R2015-2064=1%设计洪水及相应不确定性可见,以Temp和Prep为协变量的设计结果最为合理。
5 结论与讨论
在水文风险概念下,将气象因子引入到非一致性洪水频率分析中,并在给定设计使用年限情况下推求对应某一目标水文风险的非一致性设计洪水及其不确定性。该方法与常见的以时间为协变量的方法一起应用于有实测洪水资料流域的设计洪水研究,所得结论如下:(1)以气象因子为协变量时,Gumbel分布为最优洪水频率分布,其他情况下均以P-Ⅲ分布为最优洪水频率分布,比较符合我国设计洪水研究的实际情况。(2)以时间为协变量时,最优模型中位置参数为时间的线性函数;以气象因子为协变量时,最优模型中位置和尺度参数分别为年平均气温、年总降水以及年平均气温的线性函数。并且,以气象因子为协变量的最优非一致性模型优于以时间为协变量的情况。(3)以时间为协变量和以气象因子为协变量两种情况下的非一致性设计洪水及其不确定性相比于一致性假设情况存在显著差异。同时,两种非一致性设计洪水及其不确定性之间也存在着明显不同,前者由于相对不太合理的假设及参数拟合使得设计结果有所失准,而后者则提供了更具物理意义、更为可信的设计结果。
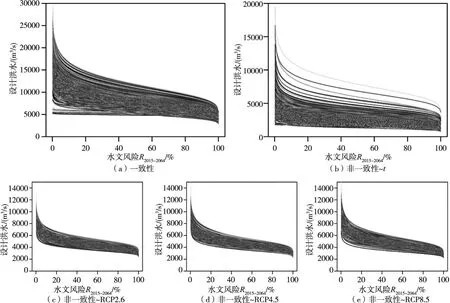
图11 设计洪水Bootstrap抽样图
本研究成果可为工程规划设计及防洪决策提供一定参考依据,但其中也存在几点值得进一步深入研究之处:(1)不同频率分布模型由于其尾部的差异性,对设计洪水量级的影响较大,因此,下一步有必要重点研究频率分布模型的选取对水文分析计算的影响。(2)本文综合比较了气象因子年统计量与季节性统计量作为协变量的拟合效果,最终选取了效果更优的年平均气温和年总降水作为气象协变量,下一步有必要进一步研究该变量与场次洪水之间的关系以及是否还有较之更为适合的协变量。(3)本文仅考虑了由于样本数据有限所引起的设计洪水统计不确定性,对于分布模型选取以及引入GCM统计降尺度数据所增加的新的不确定性没有进行研究。(4)GCM输出的未来时期气象因子预估结果最长可到2300年,时间跨度完全可以满足现行规范规定的水利水电工程合理使用年限要求。然而,对于设计期较长的情况下,GCM输出的气象协变量的预测仍存在精度较低等不足之处,因此下一步工作中考虑引入人类活动因素作为协变量,结合流域未来水利工程规划等影响,建立非一致性洪水频率分布模型,增加设计结果的可靠性。本文所选研究区域面积较大,支流众多,下一步考虑选取一些中小流域进行比较研究,以探究本文方法的普适性。
[1]郭生练,刘章君,熊立华 .设计洪水计算方法研究进展与评价[J].水利学报,2016,47(3):302-314.
[2]丁晶,何清燕,覃光华,等.论水库工程之管运洪水[J].水科学进展,2016,27(1):107-109.
[3]宋松柏,李扬,蔡明科.具有跳跃变异的非一致分布水文序列频率计算方法[J].水利学报,2012,43(6):734-739.
[4]谢平,张波,陈海健,等.基于极值同频率法的非一致性年径流过程设计方法——以跳跃变异为例[J].水利学报,2015,46(7):828-835.
[5]徐宗学,张楠.黄河流域近50年降水变化趋势分析[J].地理研究,2006,25(1):27-34.
[6]DU T,XIONG L H,XU C Y,et al.Return period and risk analysis of nonstationary low-flow series under cli⁃mate change[J].Journal of Hydrology,2015,527:234-250.
[7]XIONG L H,JIANG C,DU T.Statistical attribution analysis of the nonstationarity of the annual runoff series of the Weihe River[J].Water Science and Technology,2014,70(5):939-946.
[8]VILLARINI G,SMITH J A,NAPOLITANO F.Non-stationary modeling of a long record of rainfall and tempera⁃ture over Rome[J].Advances in Water Resources,2010,33(10):1256-1267.
[9]STRUPCZEWSKI WG,KACZMAREK Z.Non-stationary approach to at-site flood frequency modelling II.Weighted least squares estimation[J].Journal of Hydrology,2001,248(1/4):143-151.
[10]STRUPCZEWSKI W G,SINGH V P,FELUCH W.Non-stationary approach to at-site flood frequency modelling I.Maximum likelihood estimation[J].Journal of Hydrology,2001,248(1/4):123-142.
[11]STRUPCZEWSKI W G,SINGH V P,Mitosek H T.Non-stationary approach to at-site flood frequency model⁃ling.III.Flood analysis of Polish rivers[J].Journal of Hydrology,2001,248(1/4):152-167.
[12]KATZ R W,PARLANG M B,NAVEAU P.Statistics of extremes in hydrology[J].Advances in Water Resourc⁃es,2002,25(8):1287-1304.
[13]VILLARINI G,SMITH J A,SERINALDI F,et al.Flood frequency analysis for nonstationary annual peak re⁃cords in an urban drainage basin[J].Advances in Water Resources,2009,32(8):1255-1266.
[14]SALAS J D,OBEYSEKERA J.Revisiting the concepts of return period and risk for non-stationary hydrologic ex⁃treme events[J].Journal of Hydrologic Engineering,2014,19:554-568.
[15]SCHUMANN A H.Flood risk assessment and management[M].London:Springer,2011.
[16]梁忠民,胡义明,王军,等.基于等可靠度法的变化环境下工程水文设计值估计方法[J].水科学进展,2017,28(3):398-405.
[17]ROOTZÉN H,KATZ R W.Design life level:quantifying risk in a changing climate[J].Water Resources Re⁃search,2013,49:5964-5972.
[18]DAVISON A C,HINKLEY D V.Bootstrap methods and their application[M].Cambridge University Press,UK,1997.
[19]左德鹏,徐宗学,李景玉,等.气候变化情景下渭河流域潜在蒸散量时空变化特征[J].水科学进展,2011,22(4):455-461.
[20]XIONG L H,DU T,XU C Y,et al.Non-stationary annual maximum flood frequency analysis using the norming constants method to consider non-stationarity in the annual daily flow series[J].Water Resources Management,2015,29(10):3615-3633.
[21]WILBY R L,DAWSON C W,BARROW E M.SDSM-a decision support tool for the assessment of regional cli⁃mate change impacts[J].Environmental Modelling and Software,2002,17(2):147-159.
[22]NASSERI M,TAVAKOL-DAVANI H,ZAHRAIE B.Performance assessment of different data mining methods in statistical downscaling of daily precipitation[J].Journal of Hydrology,2013,492:1-14.
[23]赵芳芳,徐宗学.统计降尺度方法和Delta方法建立黄河源区气候情景的比较分析[J].气象学报,2007,65(4):653-662.
[24]COLES S G.An introduction to statistical modeling of extreme values[M].London:Springer,2001.
[25]GILROY K L,MCCUEN R H.A non-stationary flood frequency analysis method to adjust for future climate change and urbanization[J].Journal of Hydrology,2012,414:40-48.
[26]OBEYSEKERA J,SALAS J.Quantifying the uncertainty of design floods under nonstationary conditions[J].Journal of Hydrologic Engineering,2014,19(7):1438-1446.
[27]RIGBY R A,STASINOPOULOS D M.Generalized additive models for location,scale and shape[J].Journal of the Royal Statistical Society Series C-Applied Statistics,2005,54(3):507-554.
[28]AKAIKE H.A new look at the statistical model identification[J].IEEE Transactions on Automatic Control,1974,19(6):716-723.
[29]BUUREN S V,FREDRIKS M.Worm plot:a simple diagnostic device for modeling growth reference curves[J].Statistical in Medicine,2001,20:1259-1277.
[30]FILLIBEN J J.The probability plot correlation coefficient test for normality[J].Technometrics,1975,17(1):111-117.
[31]MASSEY F J Jr.The Kolmogorov-Smirnov test for goodness of fit[J].Journal of the American Statistical Associa⁃tion,1951,46(253):68-78.
[32]WILBY R L,DAWSON C W.SDSM 4.2-a decision support tool for the assessment of regional climate change im⁃pacts[Z].User Manual,2007.
[33]van VUUREN D P,EDMONDS J,KAINUMA M,et al.The representative concentration pathways:an overview[J].Climatic Change,2011,109(1/2):5-31.
[34]CHEN L,FRAUENFELD O W.A comprehensive evaluation of precipitation simulations over China based on CMIP5 multimodel ensemble projections[J].Journal of Geophysical Research:Atmospheres,2014,119.doi:10.1002/2013JD021190.

