青狮潭水库降水集合预报模式构建及应用

杨明祥，雷晓辉，蒋云钟，王 浩，何素明

（1.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038；2.广西壮族自治区水利电力勘测设计研究院，广西 南宁 530023）

1 研究背景

数值降水预报是一种客观预报手段，较主观预报方法有较大优势。然而，大气过程的混沌性和复杂性［1］，加之人类对降水发生发展机理认识有限，决定了数值模式必然存在较大不确定性。近些年来发展起来的集合预报技术，是充分考虑预报过程存在的不确定性，通过初值扰动、参数扰动等手段引入多组预报样本，从而利用多组预报结果获得比单一预报更高精度和稳定性的预报方法［2-3］。针对集合预报，国内外学者已经开展了一定的研究。文献［4］将模式中的物理过程参数化方案进行组合，形成了20个集合预报成员，采用集合平均的方式进行概率预报试验，结果表明，集合平均的结果要比单个成员的预报结论更加稳定和可靠。文献［5］采用物理过程扰动方法，构建了基于16个WRF（Weather Research and Forecasting）模式成员的中国东南地区短期集合预报系统，发现集合平均方法对于大部分气象要素场的预报效果超过单个模式成员。文献［6］基于THOPEX项目，将TIGGE集合预报应用于淮河流域的洪水预报中，取得了延长洪水预报预见期的效果。世界气象组织（WMO）认为集合预报是本世纪预报技术发展四大方向之一，并且提出了TIGGE计划［7］。针对北美预报需求，美国国家环境预报中心（National Centers for Environmental Prediction，NCEP）联合加拿大气象中心（Ca⁃nadian Meteorological Centre，CMC）开发了北美集合预报系统（North American Ensemble Forecast Sys⁃tem，NAEFS）［8］。可见，降水集合预报已经成为国内外研究的热点，产生了大量研究成果。然而，目前集合预报试验区域往往较大，针对小流域的研究还不多见。同时，当前研究多将集合样本预报技巧等同对待，采用集合平均生成最终预报结果，这种方式较为粗放，难以体现不同参数化方案针对不同研究区预报技巧的差异。

针对以上问题，本文选择位于广西暴雨中心的青狮潭水库为研究区域，通过参数化方案扰动来实现集合预报。通过WRF模式参数化方案敏感性分析，对不同参数化方案预报技巧进行定量评价，在此基础上构建集合预报方案，并开发信息化系统，以期为相关研究提供一定参考。

2 WRF模式参数化方案敏感性分析

2.1 青狮潭WRF模式构建青狮潭水库所在流域如图1所示，位于漓江支流甘棠江上，距离桂林市30 km，集雨面积474 km2，总库容6亿m3，是桂北最大水库。青狮潭水库所在区域为广西暴雨中心地带，多年平均降水量2400 mm，其下游的桂林市为著名旅游城市，为景观考虑，未修建较高的河堤，防洪能力较弱。青狮潭所处地区地形复杂，同时受季风、台风、副高等多种天气系统的影响，成云致雨机理极其复杂，数值降水预报效果受模式参数化方案影响较大。因此，采取参数化方案扰动的方式进行青狮潭流域降水集合预报，具有一定的科学和现实意义。

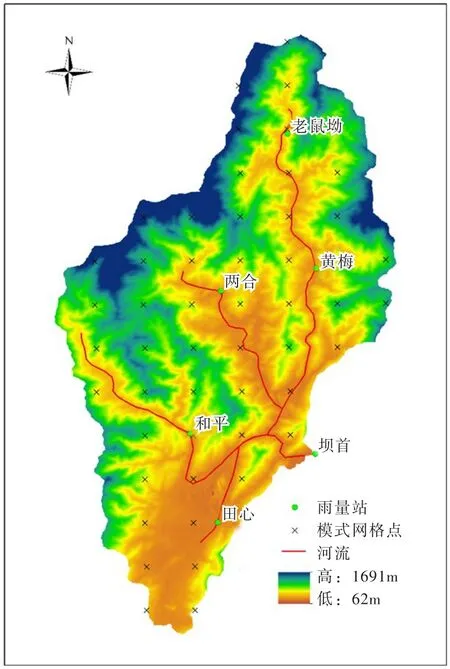
图1 青狮潭流域图

WRF模式是美国国家大气研究中心（National Center for Atmospheric Research，NCAR）和国家环境预报中心（NCEP）等部门联合开发的新一代中尺度数值天气预报系统，因其出色的动力框架和丰富的参数化方案，目前已经替代MM5成为应用最广泛的天气模式。本文基于WRF构建青狮潭流域数值降水预报模式，并针对青狮潭水库降水预报需求，综合考虑计算资源，决定采用三层嵌套方式，将WRF模式输出最内层数据的分辨率定为3 km，位于研究区域的模式网格点如图1所示。嵌套区域设置充分考虑了周边大地形和重点天气、气候系统，并尽量避免模拟中跨越气候特征或者地理特点相差巨大的区域。不同层级之间的网格设置为双向反馈关系，内层网格在接受外部网格提供的初始场和边界条件的同时也向外部网格反馈模式运行信息。本文WRF模式的初始场和边界场采用NCEP/NCAR提供的逐6 h全球分析资料（Final Operational Global Analysis，FNL），空间分辨率为1°×1°。青狮潭水库WRF模式详细参数设置如表1所示。

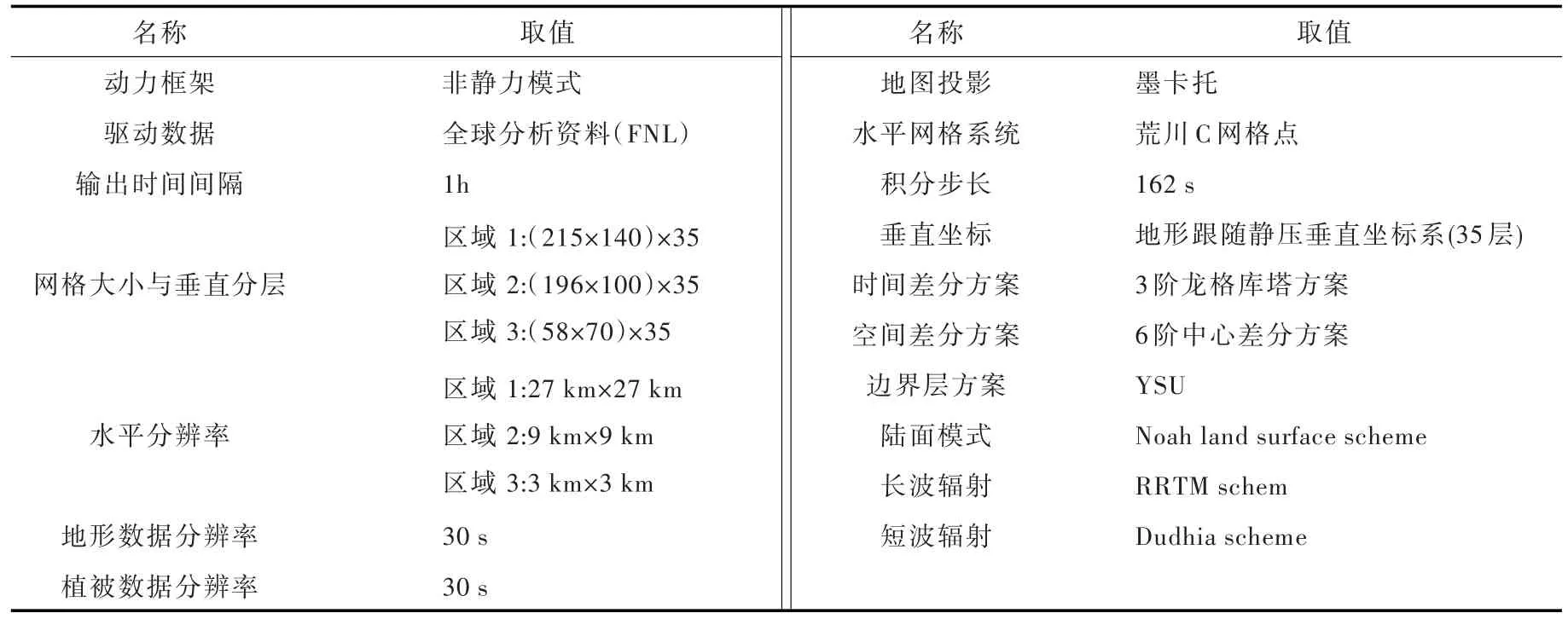
表1 WRF模式参数配置

2.2 数值降水预报定量评价方法选取ETS平均得分作为定量评价指标，ETS代表了模式的综合预报能力，取值为1时代表该次预报为完美预报，0则代表其预报技巧与随机预报相当。ETS计算公式如下［9］：

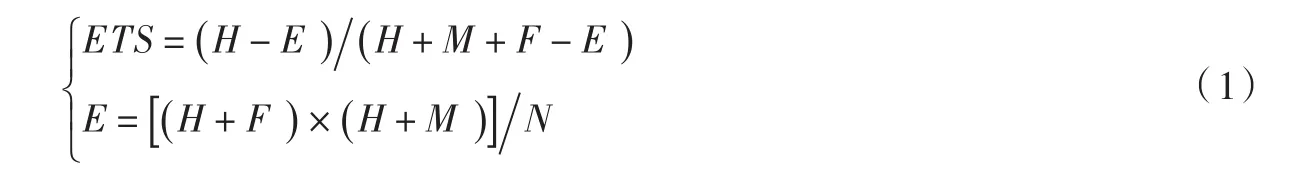
式中：H为观测值与模拟值同时大于某一阈值的站数，代表模式对某一阈值降水事件的探测能力；F为模拟值大于阈值而观测值小于阈值的站数，代表模式对某一阈值降水事件的空报倾向；M为模拟值小于阈值而观测值大于阈值的站数，代表模式对某一阈值降水事件的漏报倾向，H、M、F等指标依据表2计算；N为雨量站的个数，雨量站分布请见图1；变量E为随机预报技巧，它的加入使ETS评分能够消除随机得到的正确预报对评价的影响，因此ETS评分也叫公平预报评分。

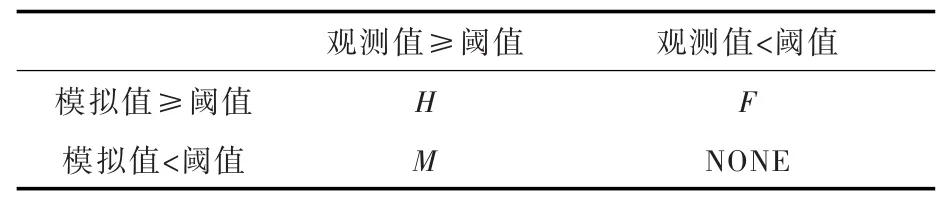
表2 降水评价列联

本研究针对降水事件选取3个阈值进行评价，阈值分别为10、25和50 mm/d。某一降水事件的ETS平均评分如下式所示：

式中：ETSevent为某次降水事件的ETS平均评价结果，ETSij即为式（1）计算的阈值j上第i个时段（24 h）的ETS评价结果；n为某次降水事件包含的时段数。

2.3 参数化方案敏感性分析WRF模式参数化方案包括辐射过程、微物理过程、边界层、积云对流和陆面过程等，其中微物理过程和积云对流参数化方案对降水的影响较大，是研究人员关注和改进的重点［10-11］。虽然WRF模式各参数化方案均有明确的物理基础，但大气现象极其复杂，且人类认识水平有限，数学方程难以精确刻画各类物理现象，导致不同参数化方案对降水模拟预报的能力相差较大，加之局部地形的影响，使同一个参数化方案在不同区域的预报技巧也存在差异。因此，基于WRF模式对研究区进行降水预报前，对参数化方案的敏感性进行分析就显得尤为重要［12］。本文选择应用较为广泛的7种不同的微物理方案（Kessler，Lin et al.（Lin）Single-Moment 3-class（WSM3）， Single-Moment 5-class（WSM5）， Ferrier， Single-Moment 6-class（WSM6）和 New Thompson（NTH））和 3种不同的积云对流参数化方案（Kain-Fritisch（KF）， Betts-Miller-Janjic（BMJ）和Grell-Devenyi（GD）），构成21个参数化方案组合，以此作为敏感性分析样本。为了能更好对比不同积云对流参数化方案和微物理参数化方案对桂林地区降水预报的影响，模拟过程中其它参数化方案保持不变，如表1所示。同时，由于本研究WRF模式最内层采用3 km分辨率，对流已不再完全是次网格尺度现象［13］，因此最内层采用纯显式云物理方案。利用1°×1°的NCEP全球再分析资料作为初始场和边界场，对2012年全年的降水情况进行了模拟。WRF模式为中尺度数值天气模式，其动力框架难以满足长期积分的需求，因此采用循环启动的方式，以4 d为一个周期，12 h为预热期（Spin-up），完成全年的数值模拟。为了提高运算效率，本研究将WRF模式部署于流域水循环模拟与调控国家重点实验室的一组计算机集群上。利用流域内6座雨量站的24 h累积降水数据，基于2.2节所述方法，对WRF模式2012年模拟结果进行ETS评分，评价结果如表3所示。

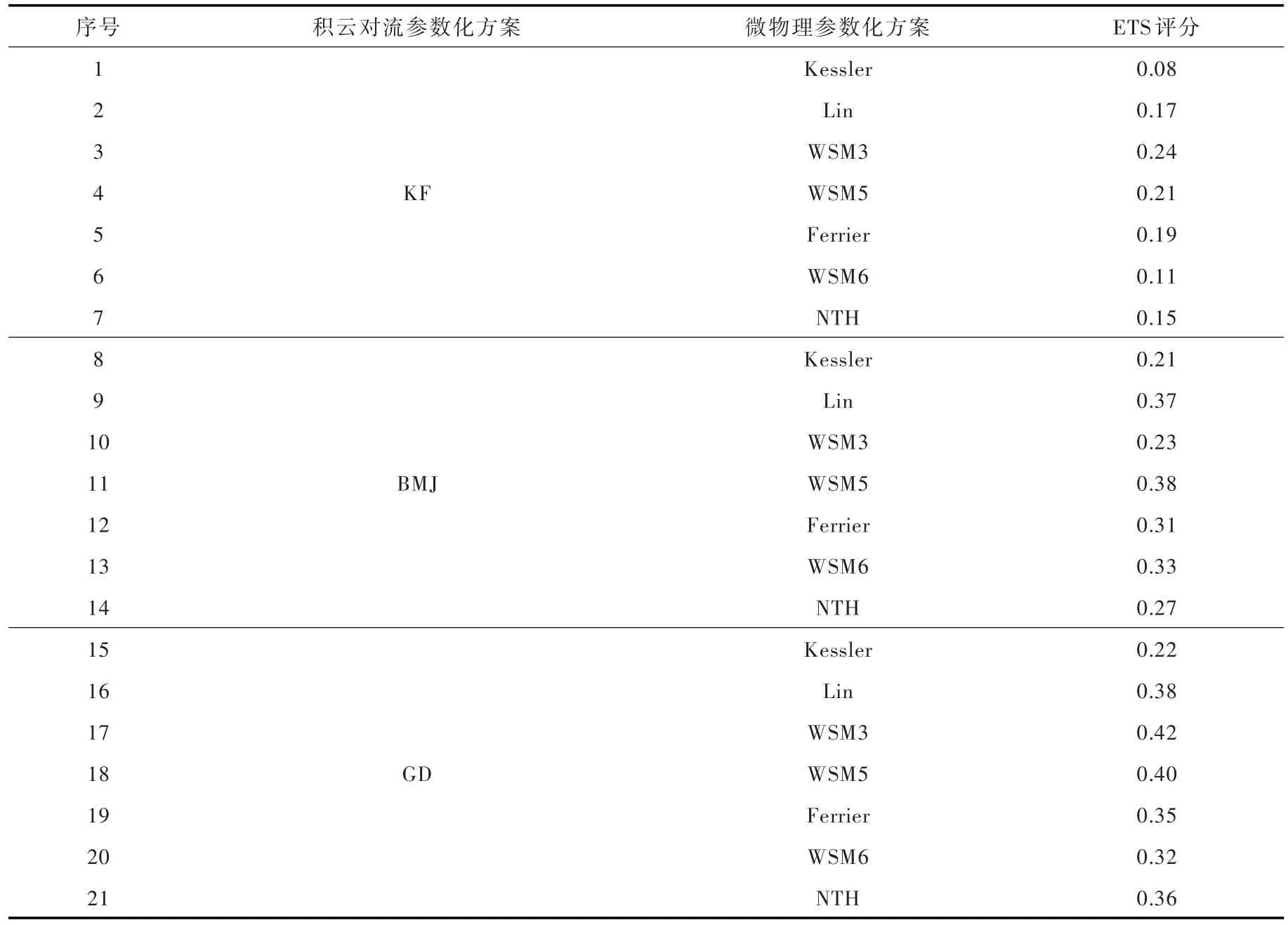
表3 微物理与积云对流参数化方案敏感性分析结果

由表3可知，各参数化方案组合在青狮潭流域均表现出一定的预报技巧，但却有明显的优劣之分。GD和BMJ积云对流参数化方案整体表现较优，而KF积云对流参数化方案则表现较差，配合各类微物理参数化方案均不能取得较高的ETS评分，甚至与Kessler微物理参数化方案的组合表现出了接近随机预报的预报技巧，说明构建的青狮潭流域WRF模式对积云对流参数化方案的选取较为敏感。Lin和WSM5微物理参数化方案的表现较为稳定，搭配合适的积云对流参数化方案能够较好的对降水情况进行模拟。在21种参数化方案组合中，WSM3与GD的组合在2012年降水模拟中表现是最优的，ETS平均评分达到了0.42，WSM5与GD的组合次之，达到了0.4。

3 降水集合预报方案构建及检验

传统基于参数化方案扰动的集合预报大多采用集合样本平均的方式，并不考虑单个集合样本的敏感性信息，但WRF模式中参数化方案往往具有一定的适用性条件，也就是针对某些具体气候特征或研究区，其预报技巧会有系统性差异，如表3所示，配置KF积云对流参数化方案的集合样本的预报效果往往较差，KF&Kessler成员的ETS评分仅有0.08。将21个参数化方案组合的结果做平均，并对其进行评价，发现ETS评分仅有0.32，低于某些集合样本的预报技巧。可见，在集合预报中，并不是集合样本越多预报效果越好。将21个集合样本按照ETS评分从高往低排序，依次累加选择样本集合，并采用式（3）来确定各个成员的权重，然后对集合加权平均结果进行ETS评分，得到2012年ETS平均评分随着集合样本数量变化情况如图2所示。

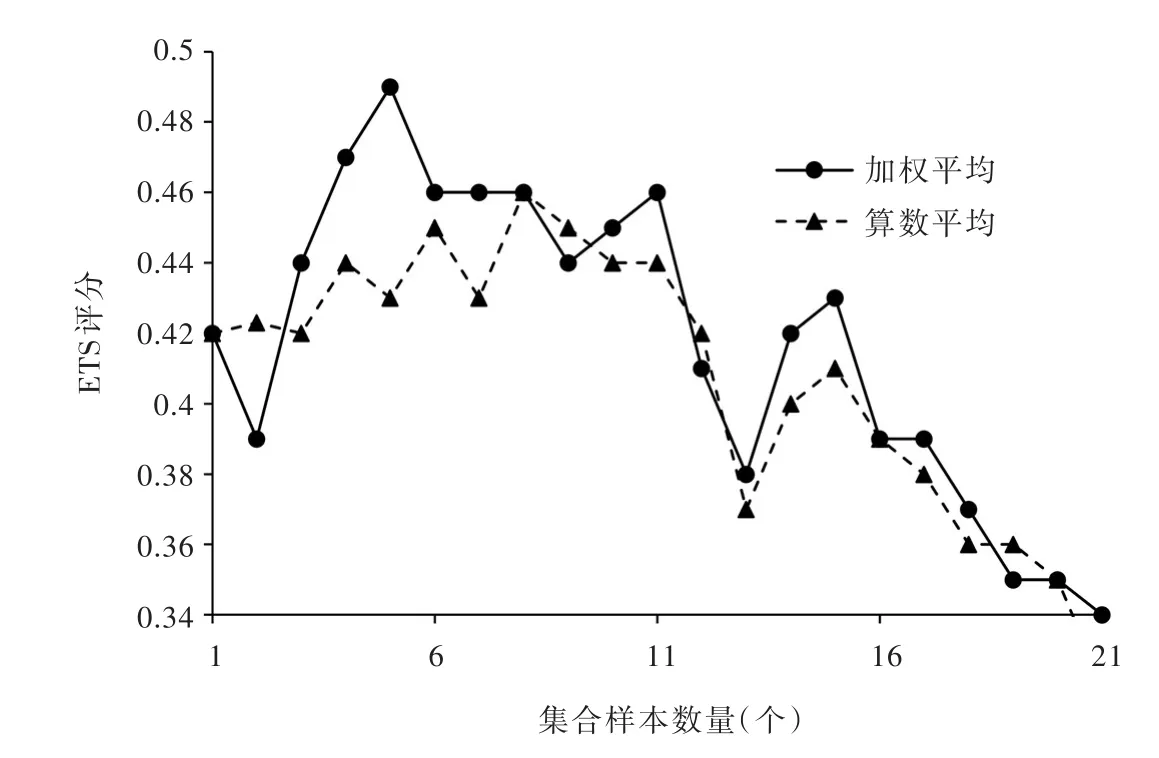
图2 集合样本预报技巧

由上图可知，随着集合样本数量的增加，其集合预报技巧整体呈现先增加后减小的趋势，并且采用集合算数平均的预报技巧整体低于相应成员加权平均的预报技巧。可见，针对具体预报对象集合样本的数量并不是越多越好，采用加权平均的预报方案能够体现不同样本预报技巧的不同，从而更好的发挥集合预报的效果，较集合算数平均的稳定性和精度更高。因此，选取ETS评分的前5位（WSM3&GD，WSM5&GD，Lin&GD，WSM5&BMJ，Lin&BMJ）作为降水集合预报成员。每次预报均使用以上5种参数化方案组合分别运行WRF模式，利用流域边界截取栅格数据形成各预报时效内的面雨量。根据ETS评分结果形成各样本的权重，分别为0.22，0.21，0.19，0.19和0.19，计算公式如下所示。

其中：Wi为第i个样本的权重，；ETSi为第i个样本的ETS评分；n为集合样本个数。

基于各样本权重，对时间序列内的面雨量做加权平均，得到集合预报的平均结果，并获取每个时段的最大值和最小值，构成上下包线。平均结果代表了预报样本的总体预报意见，计算方法如式（4）。上下包线则代表了本次预报的不确定性区间或各样本预报意见的差异性。

其中：Pi为预报成员的预报结果；P为集合预报加权平均结果。

为了进一步说明集合预报在强降水事件中的预报效果，选取2012年的4月16—19日（事件a）、5月30日—6月2日（事件b）、6月7—10日（事件c）以及6月27—30日（事件d）等4场典型降水事件对本文构建的集合预报方案进行检验，结果如图3所示。

（1）事件a，如图3（a）所示，主要降水量发生在后期，16日与17日降水量为4和8 mm，18日与19日降水量分别为22和15 mm。模式在16日与17日的上下包线区间较小，代表预报不确定性较低，且集合预报的加权平均结果分别为2.5和6 mm，很好的预报出了实际降水量级。然而，18日和19日的集合预报显示，随着预见期的延长预报不确定性迅速增大，这主要是因为实际大气现象极其复杂，初始状态的误差随着模式积分的进行而不断扩大造成的。但是，集合加权平均的预报结果在18日和19日仍然表现出了一定的预报技巧，18日集合加权平均结果为17 mm，19日集合加权平均结果为30 mm。

（2）事件b，如图3（b）所示，主要降水量发生在前期，5月30日降水量为28 mm，之后3天累积24 h降水量均在5 mm以下。模式在5月30日的预报结果上下包线区间较大，不确定性较高，而之后3天的不确定性较小。这主要是因为WRF模式对较大量级降水的预报不确定性高于较小量级降水引起的［14］。虽然5月30日预报不确定性较大，但集合预报技巧仍然较高，其预报结果为26 mm，说明加权平均使不同模式的误差得到了抵消。

（3）事件c，如图3（c）所示，是一场持续性强降水，6月7—10日，24 h累积降水量分别为37、33、10和9 mm。与事件a和事件b的预报效果类似，随着预见期的延长和实测降水量级的增加，模式预报不确定性均呈现变大的趋势。集合加权平均的预报技巧仍然较高，但在7日和8日预报中集合加权平均预报效果均低于实况，而9日和10日预报结果则略高于实况，这说明WRF模式针对较大量级降水有低报的趋势，而针对较小量级降水有高报的趋势，这与现有研究结论是一致的［15-16］。

（4）事件d，如图3（d）所示，是受副热带高压加强，低层偏南气流加强所致的大范围强降水过程，6月27日降水量达57 mm，致使漓江出现145.9 m的洪峰水位，洪峰流量达2390 m3/s。WRF模式对这场降水的模拟效果较好，27日的集合预报样本均预报出了这次强降水，且27日和28日的集合加权平均预报结果与实况数据较为接近。说明WRF模式对大范围降水的捕捉能力较强。

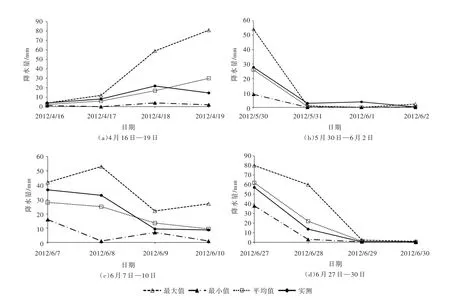
图3 集合预报试验

综上，大气过程复杂多变，具有较强的混沌效应，成云致雨机理难以被准确描述，导致基于数值模式的降水预报不确定性较大，其不确定性随着预见期的延长而迅速增加，针对小雨有高报的趋势，针对大雨有低报的趋势。但集合预报能够有效降低因单值预报带来的不确定性，利用本文所述的预报方案可有效提取不同预报样本的一致性信息，从而提高预报可靠性，是现有条件下提高预报精度的有效方法。

4 结论与展望

本文选择青狮潭水库集水区作为研究对象，建立了WRF降水预报模式，利用7种云微物理参数化方案与3种积云对流参数化方案的组合对2012年24小时累积降水进行了模拟，基于ETS评分对参数化方案敏感性进行了分析，根据样本数量对预报精度的影响，选取预报技巧在前5位的参数化方案组合作为集合预报样本，并确定了各预报样本的权重，构建了青狮潭水库集合降水预报方案。本文对集合预报方案在青狮潭降水预报中的可靠性进行了分析，发现集合预报能够有效降低因单个样本预报带来的不确定性，提升预报可靠性，是现阶段条件下提高预报精度的有效方法。然而，由于人类对自然现象认识的局限性，使得参数化方案的预报技巧随大气背景的变化而有所差异，如何运用智能挖掘方法，充分利用每个预报样本的可用信息改进总体预报效果，将成为作者未来研究的重点。此外，受计算资源限制，本研究仅选取2012年数据进行相关研究，在后续工作中将利用更多数据对研究结论进行佐证。

［1］LORENZ E N.Deterministic nonperiodic flow［J］.Journal of the Atmospheric Sciences，1969，20：130-141.

［2］TOTH Z，KALNAY E.Ensemble forecasting at NCEP and the breeding method［J］.Mon.Wea.Rev.，1997，125：3297-3319.

［3］MULLEN S L，BUIZZA R.Quantitative precipitation forecasts over the United States by ECMWF ensemble pre⁃diction system［J］.Mon.Wea.Rev.，2001，129：638-663.

［4］李刚，王铁，谭言科，等.WRF3.0参数化敏感性及集合预报试验［J］.解放军理工大学学报（自然科学版），2010，11（1）：89-96.

［5］李嘉鹏，汤剑平.WRF模式对中国东南地区的多参数化短期集合预报试验［J］.南京大学学报，2012，48（6）：677-688.

［6］包红军，赵琳娜.基于集合预报的淮河流域洪水预报研究［J］.水利学报，2012，43（2）：216-224.

［7］RICHARDSON D，BUIZZA R，HAGEDOM R.Final report of the 1st workshop on the THORPEX interactive grand global ensemble（TIGGE）［C］//WMO/TD-No.1273，WWRP-THOREX No.5.2005.

［8］CANDILLE G，BEAUREGARD S，GAGNON N.Bias correction and multiensemble in the NAEFS context or how to get a“Free Calibration”through a multiensemble approach［J］.Monthly Weather Review，2010，138（29）：4268-4281.

［9］CLARK P，GERHARD R，THOMAS F.Verification of the WRF model for simulating heavy precipitation in Al⁃berta［J］.Atmospheric Research，2014，135/136：172-192.

［10］何惠卿，王振会，金振润，等.积云参数化方案和微物理方案不同组合对台风路径模拟效果的影响［J］.热带气象学报，2009，25（4）：435-441.

［11］陈茂钦，徐海明，刘蕾，等.WRF3.1微物理参数化方案对两例暴雨的集合预报试验及可预报性分析［J］.气象科学，2012，32（3）：237-245.

［12］COLLE B A，GARVERT M F，WOLFE J B，et al.The 13-14 December 2001 IMPROVE-2 event Part III：Simu⁃lated microphysical budgets and sensitivity studies［J］ .Journal of the Atmospheric Sciences，2005，62：3535-3558.

［13］程麟生.中尺度大气数值模式发展现状和应用前景［J］.高原气象，1999，18（3）：350-360.

［14］周迪，陈静，陈朝平，等.暴雨集合预报—观测概率匹配订正法在四川盆地的应用研究［J］，暴雨灾害，2015，34（2）：97-104.

［15］王亚男.多模式降水集合预报资料的统计降尺度及误差订正研究［D］.南京：南京信息工程大学，2012.

［16］曹萍萍，陈朝平，徐栋夫，等.基于集合预报的四川夏季强降水订正试验［J］.热带气象学报，2017，33（1）：111-118.