反倾层状岩质边坡倾倒破坏的离心模型试验研究
吴 昊,赵 维,年廷凯,宋怀博,张彦君
(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
1 研究背景
具有层状结构的沉积岩、变质岩广泛分布于我国西南高山峡谷地区,随着西部大开发战略的实施,西南地区水利水电、高速公路及矿山开采等工程常涉及反倾层状岩质边坡问题,如锦屏一级水电站左岸边坡倾倒变形[1-2]、小湾水电站饮水沟大规模倾倒破坏[3]、金沙江某水电站坝肩岩体双面倾倒变形[4-5]、沪蓉西高速公路K323+185~300段反倾边坡倾倒破坏[6]、贵州开阳磷矿反倾斜坡崩塌等[7]。大型倾倒变形体一旦发生破坏,将产生规模较大的倾倒型滑坡[8-9],造成生命和财产损失。因此,针对反倾层状岩质边坡倾倒破坏的研究具有重要的现实意义。
Goodman等[10]首次提出采用基于极限平衡原理的分析方法评价反倾层状岩质边坡稳定性,陈祖煜等[11]从工程实用性角度出发,对该方法进行了改进和简化。随后,部分学者将倾倒破坏简化为悬臂梁弯曲问题,并采用极限平衡分析方法评价其稳定性[12-14]。虽然,极限平衡分析方法因其原理简单在工程中应用较为广泛,但可靠的计算结果依赖于对倾倒破坏机制的深入认识,并据此合理作出简化假设。
物理模型试验能直接观测和记录岩体的变形、破坏及其发展过程,是深入研究岩体倾倒变形破坏机制的有效手段。左保成等[15]通过室内物理模型试验研究了此类边坡的破坏模式和影响因素;杨国香等[16]、刘云鹏等[17]、范刚等[18]通过大型振动台试验探讨了其动力响应特征和破坏模式。基于离心模型试验技术,Adhikary等[13]对比研究了脆性与柔性两类岩质的反倾边坡弯曲形成机制,汪小刚等[19-20]结合龙潭水电站左岸边坡实例研究了反倾岩质边坡的变形破坏机理,Zhang等[21]发现此类边坡会产生双折线的破裂面。相比于缩尺的室内物理模型试验,离心模型试验通过再现自重应力场,可更加真实可靠地再现倾倒变形破坏过程,然而反倾层状岩体的离心模型试验所取得的成果极为有限。
目前,物理模型试验多以块状石膏混合物作为相似材料模拟节理裂隙特别发育的反倾厚层岩块式倾倒,而工程建设中常见厚度较薄的完整岩层弯曲倾倒破坏,这种工况的物理模型试验研究鲜见报道,对其弯曲倾倒破坏特征认识不足。此外,薄层反倾结构岩体弯曲变形破坏模式和坡角及岩层反倾角对其破裂面位置分布的影响探讨尚处于空白。
本文以典型地质资料为依托,概化反倾层状岩质边坡几何模型,以平板玻璃为薄层状岩层相似材料,开展4组离心模型试验,结合图像量测技术,研究不同层面倾角和边坡坡角组合情况下的坡体变形破坏特征,探究这一类边坡典型变形破坏模式及破裂面位置分布规律,为深入认识这一类边坡变形破坏机制,建立可靠的稳定性评价方法提供参考。
2 试验方案与量测技术
2.1 试验装置采用大连理工大学GT450/1.4土工鼓式离心机进行离心模型试验。该离心机鼓槽尺寸为1.4 m(直径)×0.35 m(竖向宽度)×0.27 m(径向深度),总容量为450 gt,环形模型槽的最大转速为875 r/min,此时环形鼓槽外侧离心加速度达到最大值600 g,土工鼓式离心机构造图如图1所示。
为解决高清图像采集及实时存储问题,采用GOPRO HERO4高速运动相机,通过建立无线局域网直接将高清画面传输到离心机外监测设备。设计了一套土工鼓式离心机高清图像采集的模型箱,用于固定高速运动相机以及试验模型,为捕捉高清图像,增设了LED灯片组装成的灯光补偿装置,试验模型装载于离心机中如图2所示。
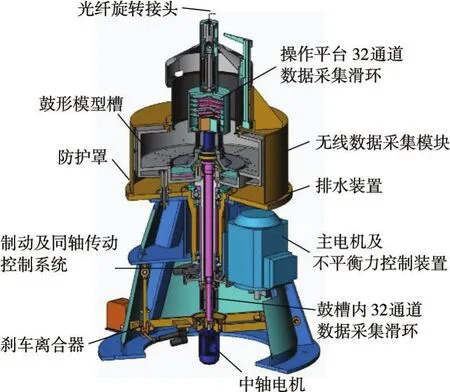
图1 土工鼓式离心机构造

图2 试验模型装载
实践证明即使离心机转速达到500 r/min,图像的采集与传输依然稳定。该测量方式具有以下特点:①能够在高离心场环境下稳定地采集及传输高清画面;②无需布置传感器,对研究对象无干扰;③能够对试验对象进行全局监测,可以记录微小变形,也可以记录较大尺度的倾倒破坏过程。
2.2 相似设计根据岩质边坡离心模型试验的相似原理,模型的几何尺寸、边界条件、荷载及相似材料的容重、强度、变形特性等方面需满足一定的相似要求。由量纲分析的一般原理,可以将岩石力学各项参数的形函数形式表达为:
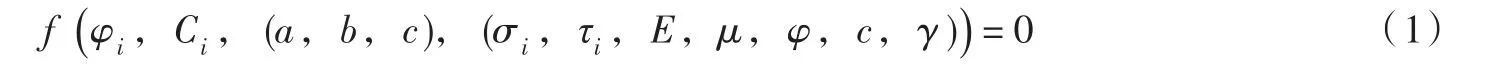
式中:φi、Ci为结构面的剪切强度;a、b、c为岩石块体和主要结构面的几何条件和方位;σi、τi、E、μ、φ、γ为岩体材料的力学特性。长若原型和模型的几何比尺CL=Lp/Lm=N,其中,Lp为原型尺寸,Lm为模型尺寸,N为离心加速度倍数,且当原型材料和模型材料的容重相等时,根据量纲分析,可以导出表1主要物理量相似关系。

表1 主要物理量相似关系
首先,平板玻璃作为一种以SiO2(占70%-73%)为主要成分的钠钙硅酸盐材料,其化学成分与岩石极为相似。此外,根据相关规范[22-23],岩体的力学参数范围与平板玻璃的力学参数列于表2,从表2可以看出,平板玻璃与岩体主要物理力学参数相似。最后,试验研究表明[24-25],平板玻璃的破坏表现为典型的脆性断裂,其破坏形式与典型的岩石破坏形式极为相似。
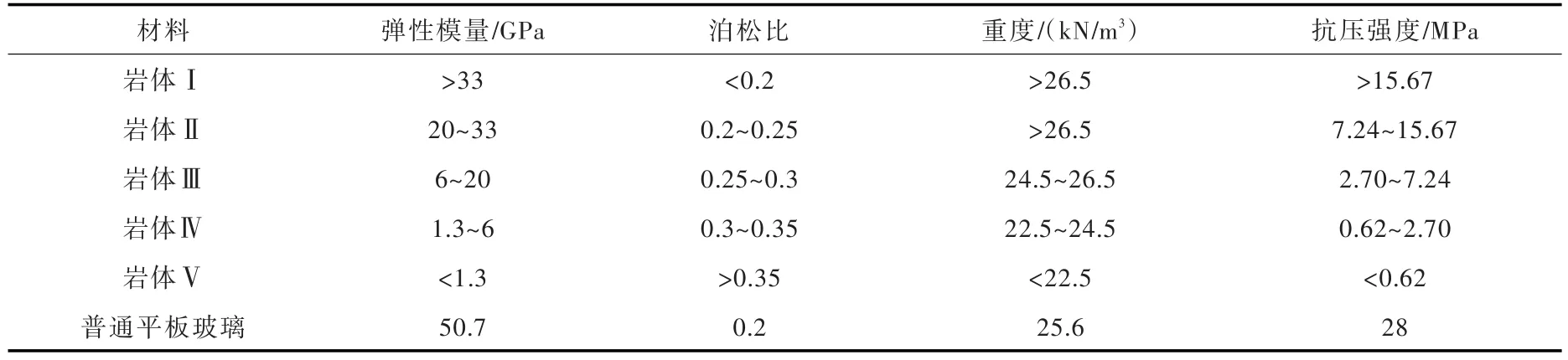
表2 材料的力学参数
综上所述,选择平板玻璃作为相似材料,可以使得原型岩体与模型材料间的力学特性相似,应力应变相同,破坏机理相同,变形相似。并且,厚度较薄的平板玻璃具有可以模拟薄层或中厚层的层状岩质边坡的优势。因此,本文相似材料选择平板玻璃,结合离心模型试验相似比尺N,选择1.6 mm厚度的平板玻璃,可以模拟层厚较薄的反倾层状岩质边坡。
2.3 试验过程地质调查表明[4-6,15-17],西南地区典型反倾层状岩质边坡工程问题常发生于边坡坡角在60°~80°之间,岩层反倾角在50°~80°之间,考虑本文离心机模型箱尺寸,本次试验概化的边坡坡角分别为60°和75°,岩层反倾角分别为60°和80°,由此开展边坡坡角及岩层反倾角不同组合形式的4组工况试验,为了对比研究,4组试验模型边坡坡高保持200 mm不变。详细试验工况列于表3。
部分藻类的油脂含量占干重的25% ~ 77%,明显高于富含油脂的陆生作物。脂肪酸链长为C15 ~ C22、不饱和水平较低的原料最适合生产生物柴油。生物柴油的制备方法包括物理法和化学法,其中物理法包括直接混合法、微乳化法,化学法包括热裂解法、酯化和酯交换法。酯交换法是制备生物柴油的常用方法,即天然油脂和醇(如甲醇)在催化剂(酸、碱、酶)作用下进行酯交换反应,生成脂肪酸酯(生物柴油)和甘油(图3)。

表3 4组离心模型试验工况
本文不考虑岩层层间力学参数变化的影响,每层平板玻璃直接接触,不添加其他材料,直剪试验表明:玻璃片层间凝聚力几乎为0,层间摩擦角约为8°,这符合真实岩层层间力学参数值。试验前,按照如图3边坡尺寸的设计,将切割后的平板玻璃分层叠加装入模型箱。以坡趾位置为基准点,按照15 mm间距绘制网格参考线,网格线交点处用红色标记点标记,作为边坡位移变化监测的参考点。试验开始前及试验过程中,通过图像量测技术,获得标记点在自定义坐标系下不同时刻的空间坐标,通过对比前后时刻标记点的空间坐标即可得到标记点的相对位移矢量。由于设备安装时标记点未能全部观测到,也有人为标记时存在的局部误差,实际4组工况下获得的有效测点位置如图3所示。
为了模拟反倾岩层由开挖卸荷导致的临空面高度增加,进而岩层受重力发生倾倒变形破坏的过程,本文采用离心梯级加载方案。首先稳步将离心机提高到85 g,稳定5 min后待边坡不再发生变形时,以10 r/min(相当于0.06 g)为一级逐步提高离心机转速,每级稳定约90 s进行下一级加载,直至边坡产生完全倾倒破坏或达到180 g设定的最大离心加速度时停止加载,加载过程离心加速度值随时间变化关系如图4所示。
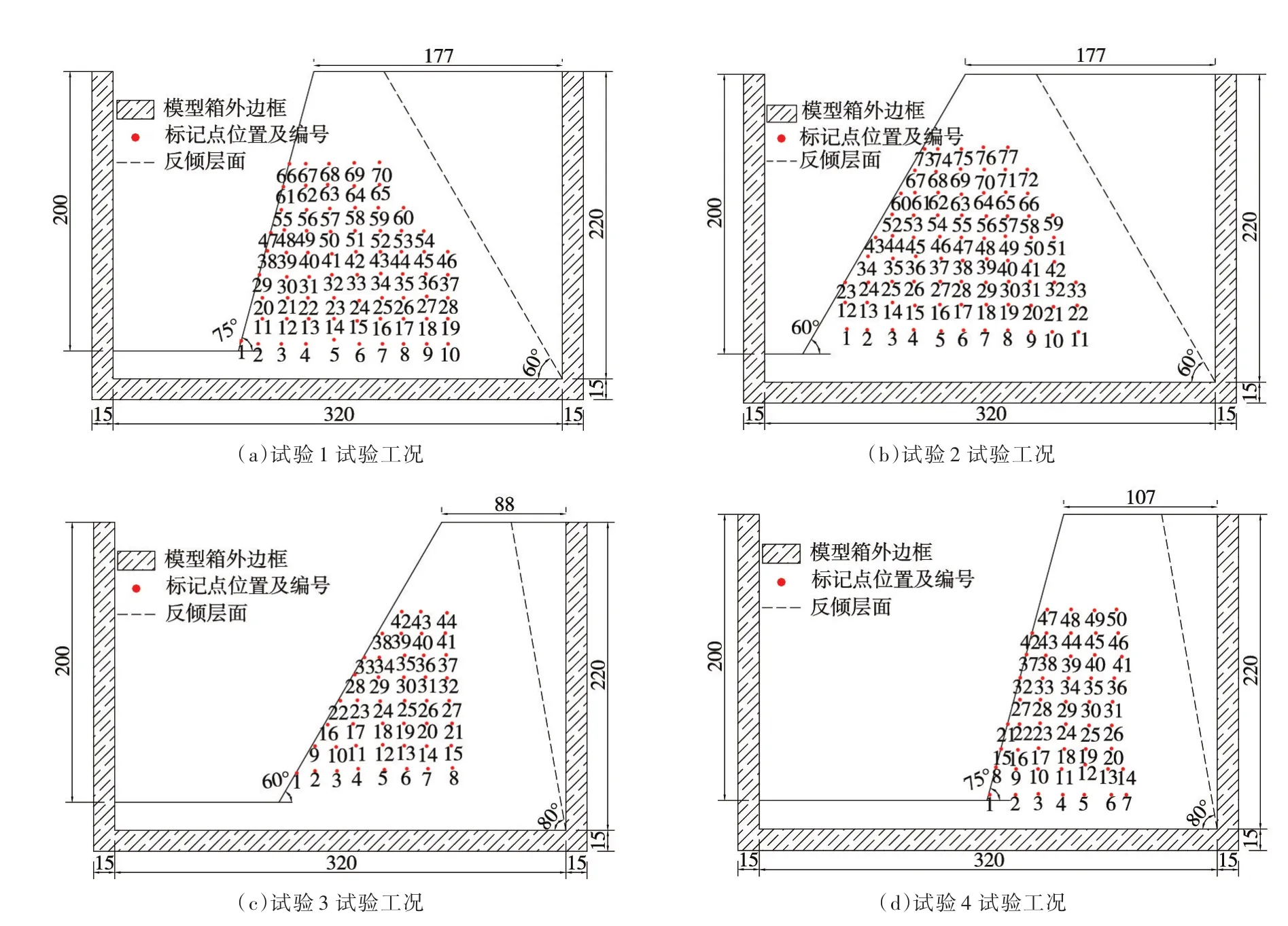
图3 4组试验工况布置侧面图(单位:mm)
3 试验结果分析
3.1 坡体变形特征4组工况边坡在发生倾倒破坏之前相对于85 g时刻累积位移矢量以及倾倒破坏后的破裂面位置如图5所示,为便于识别,显示的位移矢量放大了5倍。从图5可以看出,4组工况下边坡全场位移都很小:试验1工况,水平方向最大位移是测点67的4.99 mm,竖直方向最大位移是测点61的4.31 mm,最大合成位移为测点66的6.32 mm;试验2工况,水平方向最大位移是测点73的2.61 mm,竖直方向最大位移是测点43的5.91 mm,最大合成位移为测点43的6.20 mm;试验3工况,水平方向最大位移是测点43的3.36 mm,竖直方向最大位移是测点28的5 mm,最大合成位移为测点28的5 mm;试验4工况,水平方向最大位移是测点47的4.28 mm,竖直方向最大位移是测点37的2.60 mm,最大合成位移为测点47的4.86 mm。平板玻璃作为一种脆性材料,且弹性模量较大,受离心场荷载边坡全场变形量较小,这符合一般规律。
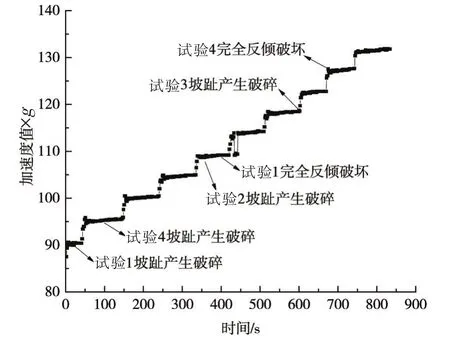
图4 4组工况坡体破坏时临界加速度值
虽然4组工况坡体累积位移量都较小,但是坡体位移矢量基本上可以按照潜在的破裂面分为两部分:一部分是潜在破裂面以下岩体,该部分坡体累积位移量相对较小且主要以竖向位移为主;另一部分是潜在破裂面以上岩体,该部分坡体累积位移量相对较大,且越靠近坡顶位置合成位移量越大,坡趾位置在坡体倾倒破坏前基本无水平方向的相对位移量。此外,坡表的位移矢量基本平行于潜在破裂面。据此可以看出,坡体变形主要发生在潜在的破裂面以上岩层部分,该部分可以看作是组合悬臂梁,岩层潜在破裂面以下部分可以看作组合悬臂梁锚固约束固定端,忽略其变形;从坡趾位置的变形可以看出,该部分岩体起到抗倾倒作用,对岩层倾倒变形发展起到至关重要的作用。
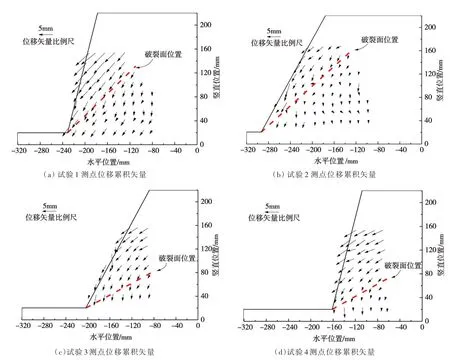
图5 4组工况测点位移累积矢量
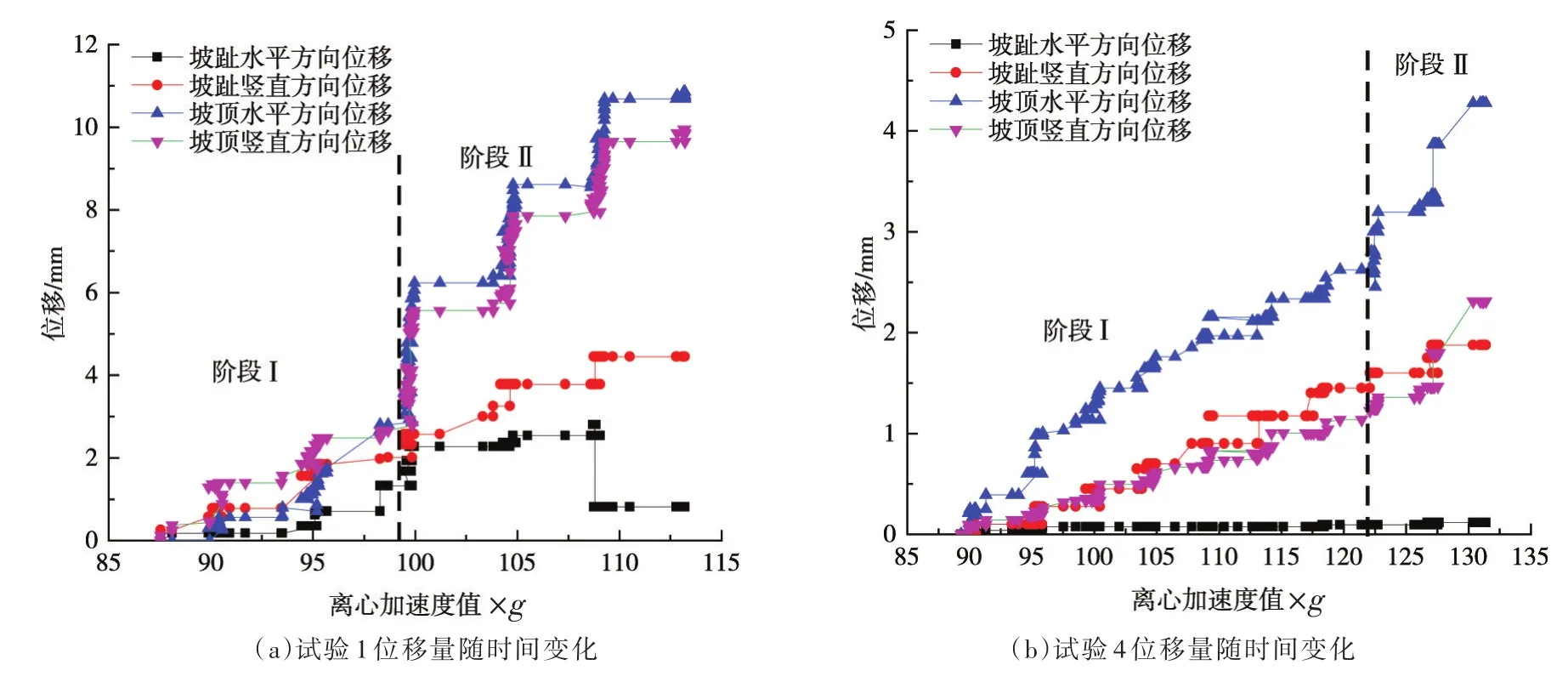
图6 位移随离心加速度的变化曲线
由于试验1与试验4两种工况坡体发生完全倾倒破坏,因此选取两种工况下坡趾与近坡顶处测点(试验1工况分别是测点1和66,试验4工况分别是测点1和47),对比其位移随离心加速度值的变化关系,如图6所示。从图6可以看出,可以将近坡顶位移量随时间变化分为两阶段:阶段Ⅰ是位移量稳步增长阶段,阶段Ⅱ是位移量加速增长阶段。当位移量随离心加速度值变化属于阶段Ⅰ时,边坡处于相对稳定状态,随着离心加速度进一步提高,到达某一g值时,边坡位移量随离心加速度值变化转变到阶段Ⅱ,此时边坡由阶段Ⅰ的相对稳定状态转变到阶段Ⅱ非稳定状态,坡体在此阶段极易发生瞬时的倾倒破坏。此外,根据图6可以观察到,试验1工况下近坡顶测点处水平方向与竖直方向位移量保持同等大小增量增加,而试验4工况下坡趾或近坡顶测点处水平方向位移增量明显大于竖直方向位移增量,其本质原因是两组工况近坡顶测点位移发展方向不同,这进一步说明,潜在破裂面以上坡体部分位移矢量方向与潜在破裂面平行向下,而不同工况下坡体破裂面位置明显不同。
3.2 坡体倾倒破坏特征边坡的临界坡高定义为模型边坡高度乘以达到模型边坡破坏时的离心加速度值,其可以反映边坡的极限承载能力。试验结果显示,不同边坡角度及岩层反倾角度组合条件下,边坡的极限承载能力不同,并且边坡破坏时的破裂面分布位置不同。
如图4所示,记录4组工况坡体倾倒破坏发生时的临界加速度值。试验1工况下,当离心加速度值达到90.2 g时,坡趾产生破碎,当离心加速度值达到109 g时,边坡发生完全倾倒破坏,试验4工况下,当离心加速度值达到95.5 g时,边坡坡趾产生破碎,当离心加速度值达到127 g时,边坡发生完全倾倒破坏,试验2与试验3两组工况下,边坡坡趾产生破碎时的离心加速度值分别在109 g与122.2 g,然而一直到离心机稳步加载到180 g时,试验2与试验3两种工况边坡依然未发生明显的倾倒破坏,只产生了部分岩层断裂的现象。经计算,边坡坡趾产生破碎时,4组工况分别对应的边坡临界坡高为:18.04、21.80、24.44与19.10 m;试验1与试验4两组工况坡体产生完全倾倒时对应的边坡临界坡高分别为21.80和25.40 m,而试验2和试验3两组工况边坡坡高直到36 m依然未发生完全倾倒破坏。如图7所示,坡体倾倒破坏基本是沿着过坡角且约高于层面垂线某一角度的破裂面产生,通过对4组工况边坡破裂面与层面垂线夹角的测量,得到以下结果:4组工况该角度分别为12.43°、10.28°、16.64°与 17.57°。

图7 4组工况离心加载产生破坏情况
4 倾倒破坏模式和破裂面位置分析
4.1 倾倒破坏模式分析通过4组反倾层状岩质边坡倾倒破坏的离心模型试验,得出上述坡体变形及破坏特征,结合图8边坡倾倒破坏过程不同阶段的实物图(以试验1工况为例),将整个边坡倾倒破坏过程概化成图9的素描简图,分成以下4个主要阶段:
(1)坡趾岩层断裂。反倾层状岩质边坡坡趾处往往受到上部岩层的挤压作用,离心模型试验中,离心加速度提高到一定程度时,坡趾岩层产生断裂,在实际工程中,通常表现为反倾层状结构岩层开挖卸荷,达到某一开挖深度后,开挖坡趾处岩层产生断裂,如图9(a)所示。
(2)近坡顶张拉裂缝产生。反倾层状岩质边坡倾倒破坏存在一个变形倾倒区和一个稳定区,稳定区位置位于坡体后缘,该部分在整个变形破坏过程中,变形有限,坡体处于稳定状态,而变形倾倒区坡体随着离心加速度的提高,进一步产生变形,特别在靠近坡体后缘稳定区处呈现明显的沿着破裂面平行方向的位移,因此,当离心加速度达到某一g值时,近坡顶张拉裂缝产生,如图9(b)所示。
(3)岩层折断渐进式延伸。坡趾位置受到坡体上部推力,产生剪断式破坏,远离坡趾位置的岩层在离心场作用下首先产生弹性弯曲变形,当弹性弯曲变形达到极限值后,进而岩层产生折断,岩层的折断现象从坡趾开始沿着直线型破裂面渐进式向近坡顶方向延伸,如图9(c)所示。
(4)裂缝贯通瞬间倾倒。坡体在发生完全倾倒破坏之前,坡体变形发展缓慢且变形量较小,随着离心力提升,岩层渐进式折断,变形倾倒区坚硬的完整岩柱逐一被次级节理切割,反倾层状岩质边坡倾倒破坏模式由完整岩层的弯曲式倾倒转变为岩块式倾倒破坏。当坡体后缘张拉裂缝与岩层折断裂缝贯通后,进一步提高离心加速度,坡体产生瞬间倾倒破坏,如图9(d)所示。

图8 倾倒破坏不同阶段特征(试验1工况为例)
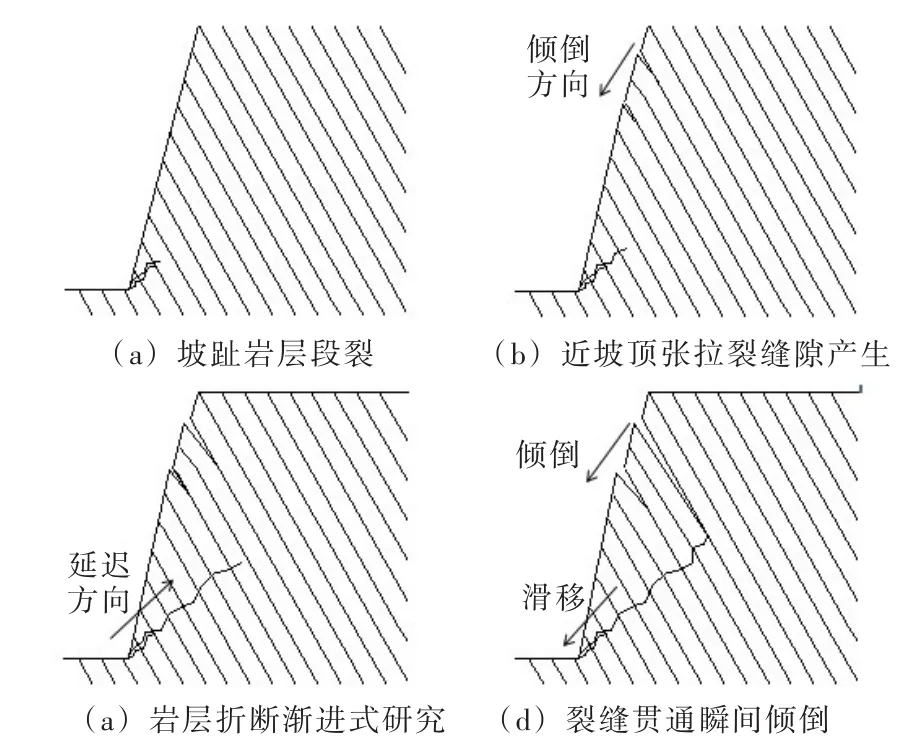
图9 坡体倾倒破坏模式
4.2 倾倒破裂面位置分析本文研究进一步证实反倾层状岩质边坡倾倒破坏是沿着过坡趾直线型的破裂面产生,该面位于层面法线以上且呈θ夹角,最初Aydan等[12]提出的悬臂梁型极限平衡理论分析中θ=0,后来Adhikary等[13-26]通过试验得到q的合理范围在12°~20°,然而Aydan等[27]最新的模型试验结果表明θ的范围为0°~15°,由此可见,目前对破裂面与层面法线交角尚无统一认识。由上述试验结果分析可得,边坡坡角的改变对θ角的影响不大,而岩层反倾角的改变对θ角的影响显著,θ随着岩层反倾角增大而增大。
破裂面位置的确定对开挖高边坡及基坑工程意义显著,实际工程中对其位置的确定通常具有一定的主观性。由上述倾倒破坏模式分析可知,在岩层折断之前,最初岩层仅产生微小的弹性弯曲变形,图3则表明岩层折断前靠近坡顶表面岩层弹性变形产生的位移矢量基本是平行于潜在的破裂面向下。据此,对于反倾结构岩层的开挖支护及倾倒变形体的防治,可依据监测近坡顶得到的水平向及竖直向位移计算其潜在的破裂面位置,进而确定支护方案和支护位置。由本文4组工况近坡顶表面多个测点位移矢量方向计算得到θ角平均值,对比其破坏后量测得到的真实值,列于表4。计算值结果虽稍大于真实值,但可反映破裂面的真实位置,为实际工程反倾层状岩质边坡破裂面位置的确定提供科学依据。

表4 4组工况θ角真实值与计算值对比
5 结论
通过4组反倾层状岩质边坡倾倒破坏的离心模型试验及其数字图像处理分析,得到如下结论:(1)反倾层状岩质边坡倾倒变形主要发生在潜在破裂面以上,坡趾位置整体位移量小,坡趾位置岩层起到抗倾倒作用;近坡顶位移增量可以分为稳定增长和加速增长两个阶段,分别对应坡体稳定状态和坡体不稳定状态;(2)反倾层状岩质边坡倾倒破坏模式可概化4个阶段:(a)坡趾岩层断裂;(b)近坡顶张拉裂缝产生;(c)岩层折断渐进式延伸;(d)裂缝贯通瞬间倾倒。前两个阶段主要发生在近坡顶位移量稳定增长阶段,而后两个阶段主要发生在近坡顶位移量加速增长阶段;(3)倾倒破坏是沿着经过坡趾的一直线型破裂面产生,边坡坡角的改变对破裂面位置影响不大,而岩层反倾角的改变对其影响显著,可以通过监测近坡顶表面岩层弹性变形产生的位移矢量方向预测潜在破裂面位置,这为边坡稳定性评价及边坡支护提供参考。(4)通过本试验结果可以看出,由平板玻璃作为岩石相似材料开展的离心模型试验可以得到理想的试验结果,这为岩体相似材料的选择提供新的思路,可进一步以平板玻璃作为相似材料深入研究岩层间力学参数、岩层厚度及其他外部营力作用等因素影响的反倾层状岩质边坡的科学问题。
[1]徐佩华,陈剑平,黄润秋,等.锦屏水电站解放沟反倾高边坡变形机制的探讨[J].工程地质学报,2004,12(3):247-252.
[2]刘造保,徐卫亚,金海元,等.锦屏一级水电站左岸岩质边坡预警判据初探[J].水利学报,2010,41(1):101-107.
[3]杨根兰,黄润秋,严明,等.小湾水电站饮水沟大规模倾倒破坏现象的工程地质研究[J].工程地质学报,2006,14(2):165-171.
[4]王启国,颜慧明,刘高峰 .金沙江虎跳峡水电站上江坝址若干关键工程地质问题研究[J].水利学报,2012,43(7):816-825.
[5]邱俊,任光明,吴龙科,等.金沙江某水电站左坝肩岩体双面倾倒形成机制[J].山地学报,2016,34(1):77-83.
[6]卢海峰.巴东组软岩边坡岩体工程特性及破坏机理研究[D].北京:中国科学院研究生院,2010.
[7]郑达,黄润秋,黄刚.地下开采作用下“反倾上硬下软”型斜坡崩塌形成机制研究--以贵州开阳磷矿崩塌为例[J].工程地质学报,2014,22(3):464-473.
[8]李果,黄润秋,巨能攀,等 .汶川地震诱发干河口巨型反倾滑坡成因机制研究[J].水电能源科学,2011,29(4):118-121.
[9]王剑梅.反倾层状岩体倾倒变形的力学机制分析及其早期识别指标体系研究[D].成都:成都理工大学,2015.
[10]GOODMAN R E,BRAY J W.Toppling of rock slopes[C]//Proceedings of ASCE Specialty Conference,Rock En⁃gineering for Foundations and Slopes.Colorado:Boulder,1976.
[11]陈祖煜,张建红,汪小刚 .岩石边坡倾倒稳定分析的简化方法[J].岩土工程学报,1996,18(6):92-95.
[12]AYDAN O,KAWAMOTO T.The stability of slopes and underground openings against flexural toppling and their stabilisation[J].Rock Mechanics&Rock Engineering,1992,25(3):143-165.
[13]ADHIKARY D P,DYSKIN A V.Modelling of progressive and instantaneous failures of foliated rock slopes[J].Rock Mechanics and Rock Engineering,2007,40(4):349-362.
[14]卢海峰,刘泉声,陈从新 .反倾岩质边坡悬臂梁极限平衡模型的改进[J].岩土力学,2012,33(2):577-584.
[15]左保成,陈从新,刘小巍,等.反倾岩质边坡破坏机理模型试验研究[J].岩石力学与工程学报,2005,24(19):3505-3511.
[16]杨国香,叶海林,伍法权,等.反倾层状结构岩质边坡动力响应特性及破坏机制振动台模型试验研究[J].岩石力学与工程学报,2012,31(11):2214-2221.
[17]刘云鹏,黄润秋,邓辉.反倾板裂岩体边坡振动物理模拟试验研究[J].成都理工大学学报(自科版),2011,38(4):413-421.
[18]范刚,张建经,付晓.含泥化夹层反倾岩质边坡动力响应的大型振动台试验[J].地震工程学报,2015,37(2):422-427.
[19]汪小刚,贾志欣,陈祖煜,等.岩质边坡倾倒破坏的稳定分析方法[J].水利学报,1996(3):7-12.
[20]汪小刚,张建红,赵毓芝,等 .用离心模型研究岩石边坡的倾倒破坏[J].岩土工程学报,1996,18(5):14-21.
[21]ZHANG J H,CHEN Z Y,WANG X G.Centrifuge modeling of rock slopes susceptible to block toppling[J].Rock Mechanics and Rock Engineering,2007,40(4):363-382.
[22]中华人民共和国水利部 .GB/T50218-2014,工程岩体分级标准[S].北京:中国计划出版社,2014.
[23]中国建筑科学研究院.JGJ102-2003,玻璃幕墙工程技术规范[S].北京:中国建筑工业出版社,2003.
[24]李维红.玻璃材料在双向应力下失效分析的数值模拟与失效准则的验证[D].大连:大连理工大学,2005.
[25]张明,卢裕杰,介玉新,等.不同加载条件下岩石强度尺寸效应的数值模拟[J].水力发电学报,2011,30(4):147-154.
[26]ADHIKARY D P,DYSKIN A V,JEWELL R J,et al.A study of the mechanism of flexural toppling failure of rock slopes[J].Rock Mechanics&Rock Engineering,1997,30(2):75-93.
[27]AYDAN O,AMINIM M.An experimental study on rock slopes against flexural toppling failure under dynamic loading and some theoretical considerations for its stability assessment[J].Journal of the College of Marine Sci⁃ence&Technology Tokai University,2009,7(2):25-40.

