水电机组振动劣化预警模型研究及应用
桂中华,张 浩,孙慧芳,张 飞
(1.国网新源控股有限公司 技术中心,北京 100161; 2.国网浙江省电力公司,浙江 杭州 310008)
1 研究背景
振动稳定性关系到水电机组乃至整个水电站能否正常运行,随着水电机组单机容量和尺寸的不断增大,机组相对刚度下降,运行中的机组振动稳定性问题日益突出。国内五强溪、小浪底、李家峡、东江电站转轮都曾因振动而引起叶片裂纹问题[1-3];江苏宜兴抽蓄电站在试运行阶段出现导水机构小开度自激振动[4];河北张河湾抽蓄电站水轮机工况运行时的强烈振动和噪声等[5]。这些振动问题导致机组部件的损坏、机组运行中断,甚至影响到电厂和电网的生产和运行安全,但由于人们对水电机组振动稳定性问题的认识较晚,加之问题本身的复杂性,对该问题的认识至今仍不全面[6-7]。
随着传感器技术、计算机技术和数据处理技术的进步,水电行业开展了大量的振动监测与故障诊断方面的研究,并开发了水电机组稳定性监测系统,如TN8000、PSTA2003等,大都安装有振动、摆度、压力脉动等传感器,实现机组振动状态在线监测、越限报警及分析诊断等功能[8]。国外也有团队研究开发了抽水蓄能机组的监测系统,分析了机组的不同振动水平,针对不同类型的故障进行了举例说明,如发电机、轴承、支撑结构、空化等,并对故障进行了振动信号和频谱的分析[9]。这些成果对预防机组振动事故起到了一定的积极作用。但现有研究基本采用振动监测值与单一限值的比较来实现越限预警报,其振动限值通常参考相关国家标准、行业标准,以及厂家建议值等来确定,这种绝对值比较法存在不能反映机组个性特色、适用机组运行工况有限的缺点,其报警实用性有待提高[11-14]。
本文利用机组健康状态下振动样本数据,计算出典型工况振动的健康区间,进而建立振动预警模型,该模型可为机组不同运行工况提供预警保护,有效弥补传统预警法仅能对机组稳定运行工况进行保护的不足。同时模型可利用机组振动历史数据进行自学习,更新振动预警模型,提高预警准确性。
2 机组振动预警的统计理论
2.1 莱以特准则(3σ准则)3σ准则是最常用的一种检查异常数据的准则。对某一次观测,如果观测值偏离总体期望的偏差服从正态分布N(μ,σ2),那么可采用区间(μ-3σ,μ+3σ)作为判断此次观测值是否超限的依据。
2.2 振动信号的正态分布特性水电机组振动数据测量的随机误差是由多种相互独立的因素引起的微小误差的总和,包括运行条件的波动、测量仪器的灵敏度以及随机干扰等。随机误差具有明显的统计分布特征,一般服从正态分布规律。通过多个电站振动数据的统计分析,发现机组振动信号符合正态分布规律。
本文以某水电站2号机组为案例,选取该机组在额定水头和额定负荷下20 s的振动和摆度实测信号进行统计分析。在振动摆度物理参数中通常采用振动混频幅值作为评价机组运行稳定性的参数,通过计算得到分析时段内,振动混频幅值的均值和标准差见表1。将各个信号的峰峰值从最大值到最小值均分为100个区间,统计振动信号峰峰值落在每个区间内的个数,进而求出每个区间的概率密度,结果如图1所示,同时在图中还绘制了与振动信号具有相同均值和标准差的标准正态分布。通过实测振动和标准正态分布的概率分布密度函数比较,可以看出机组振动信号具有明显的正态分布规律。

表1 实测振动信号的统计参数
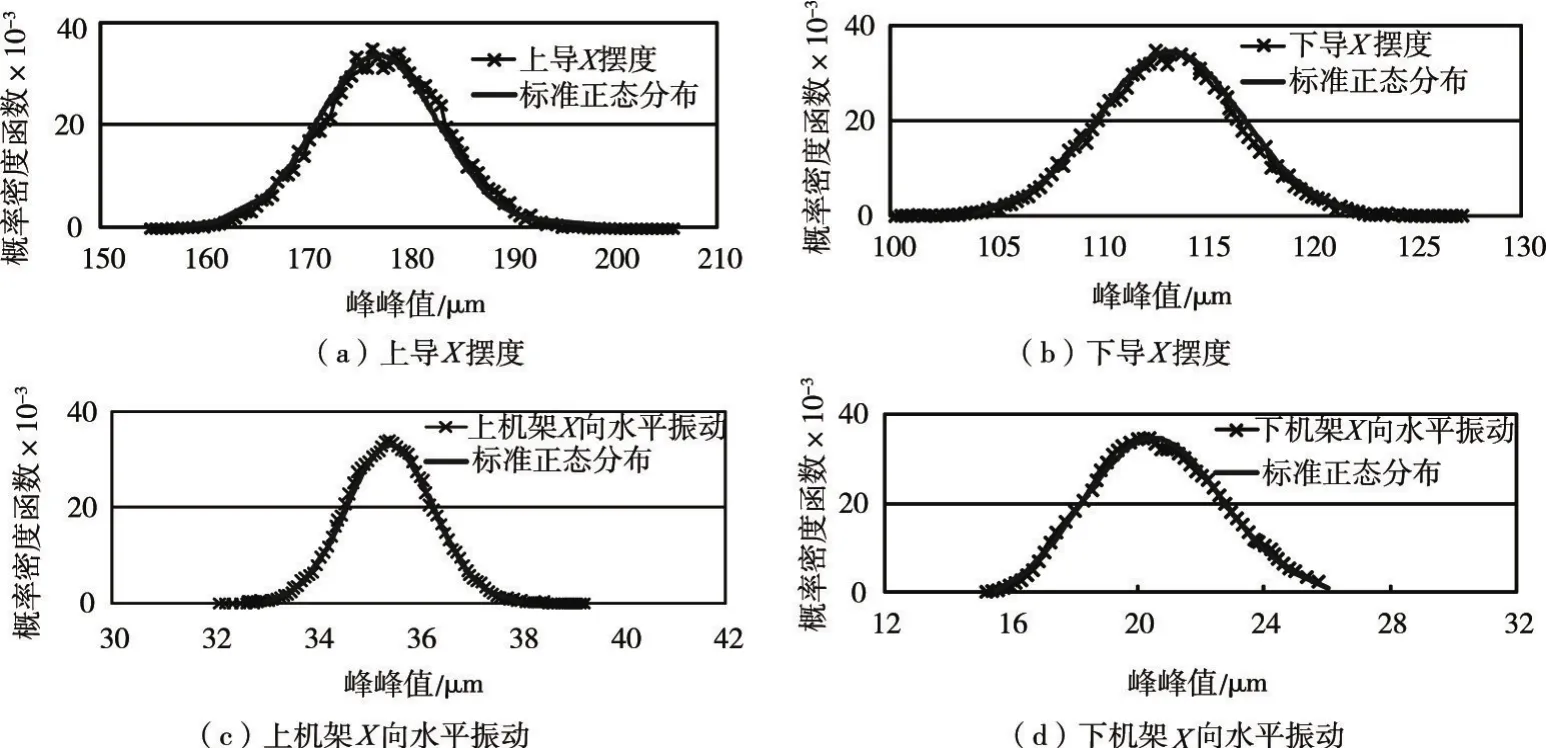
图1 实测振动信号与标准正态分布的概率密度函数比较
2.3 振动预警限值的确定上述分析表明振动信号的混频幅值服从N(μ,σ2)的正态分布,因此,对于振动混频幅值,可根据莱以特准则确定其预警限值区间为,其中、S是μ、σ的无偏估计,可按下列公式求取:
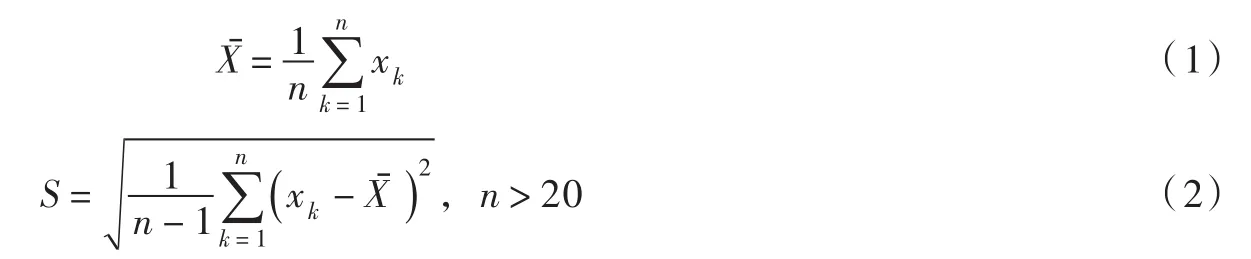
由于振动与机组运行工况紧密相关,在计算预警区间如果不考虑工况差异,会导致样本分散,标准偏差大,不利于预警区间的准确确定。因此,在计算预警区间时,需先将健康样本按工况条件进行区分,如按一定的功率范围、水头范围等,不同的工况应分别确定不同的预警区间。
3 振动劣化预警的建模方法
建立水电机组振动劣化预警模型时,应先选取机组健康状态下的振动数据,进行适当预处理,得到正常状态的振动记录;然后对机组运行工况进行细分,确定若干典型工况;最后计算典型工况的振动健康区间,建立振动预警模型,其建模流程如图2所示。
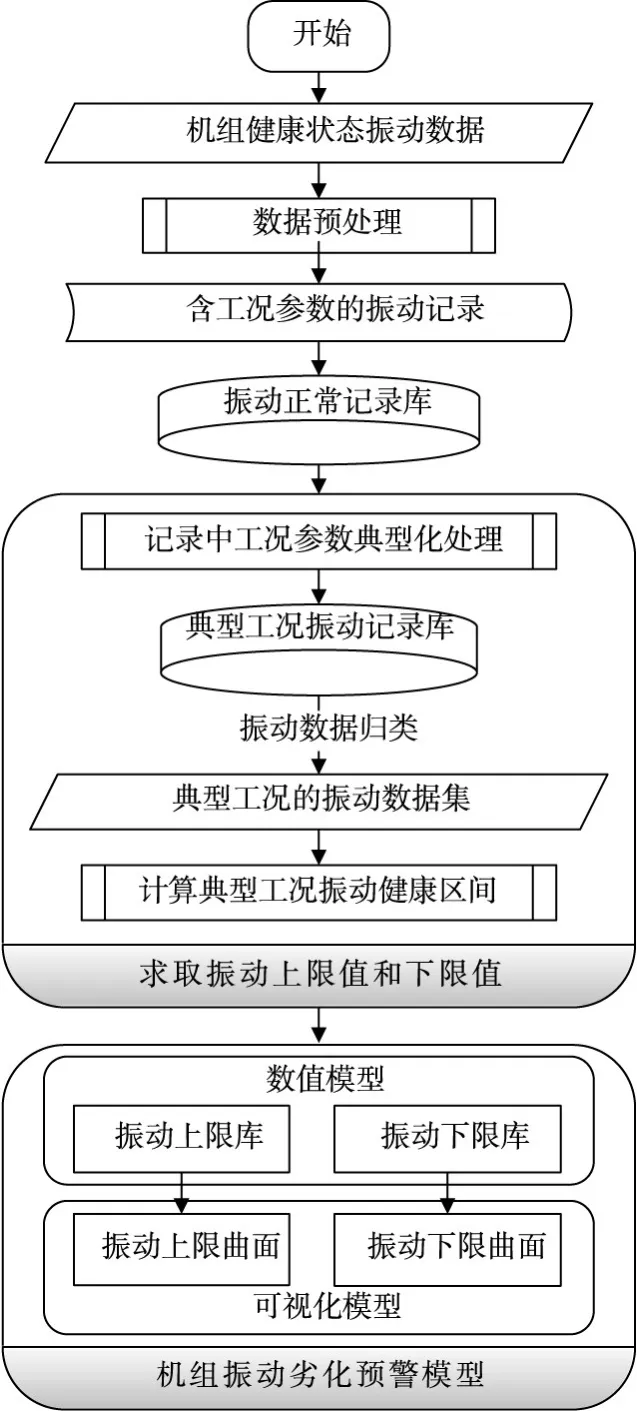
图2 振动状态劣化预警建模流程
(1)建模数据选取。建模的数据应选取机组健康状态时的振动值,主要来源:新投产机组的调试试验数据;老机组的大修后试验数据;机组运行状态良好时段内稳定性监测系统采集到的振动数据。
(3)建立机组振动正常记录库。将收集到的所有振动正常数据,按照进行表示,得到振动正常记录,并存入振动正常记录库。
(4)确定机组典型工况。水电机组的振动与工况密切相关,但当两个工况的水头之差△H和负荷之差△P足够小时,其振动差异可以忽略,可近似当作相同工况。据此,可将水电机组运行工况按照水头、负荷划分为若干典型工况,表示为。
(5)建立典型工况振动记录库。按照下列原则对振动正常记录的工况参数进行处理,将振动正常记录中的有功和水头参数转换为典型工况参数。
对振动正常记录库里所有记录进行上述处理后,得到典型振动记录库。
(6)典型工况振动记录的归类。将典型工况振动记录库中的记录按照有功和水头进行归类,即具有相同的有功和水头的记录归为同一类记为,并提取其振动值得到集合。
以数值模型中上限记录的有功、水头和上限值作X、Y、Z坐标,在三维坐标系中将所有上限记录对应的点连起来,即可得到上限曲面;同理可得到下限曲面,从而建立起可视化预警模型。
4 振动劣化预警的应用
4.1 预警模型的建立下面以国内某水电站的2号机组为研究对象,将振动状态劣化预警模型与机组原有振动稳定性监测系统相结合,建立了机组振动监测及劣化预警系统,实现机组运行工况范围内的振动预警。该机组原振动稳定性监测系统的主要监测参数见表2。
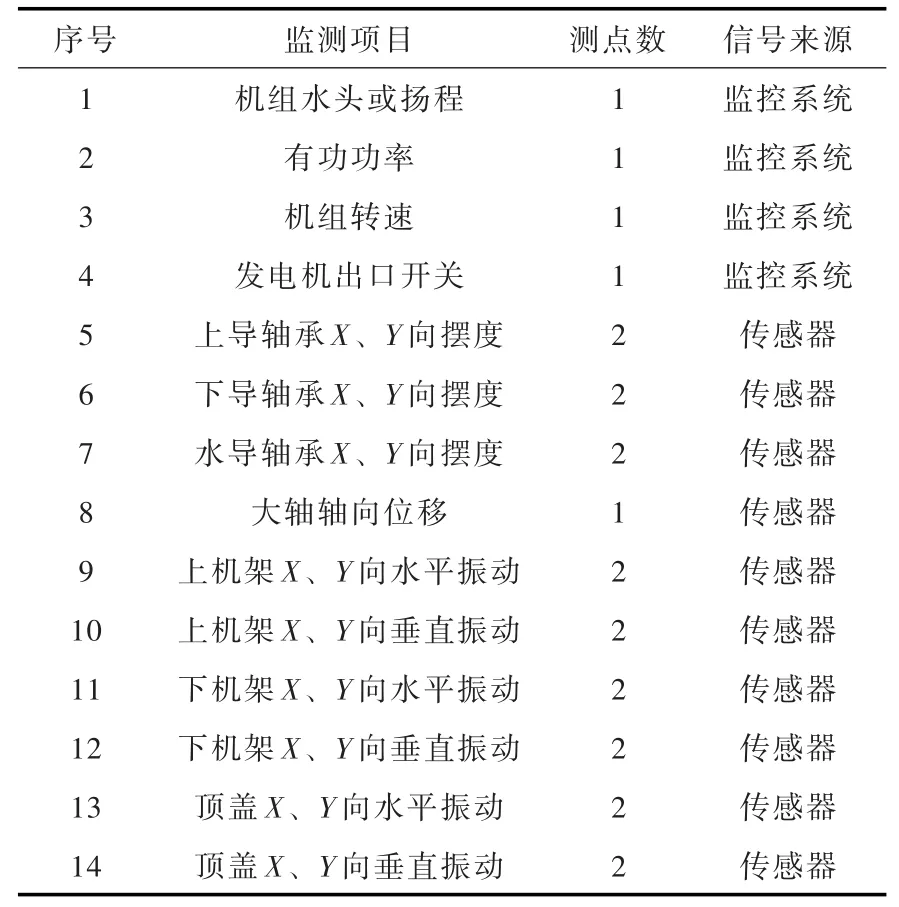
表2 振动稳定性监测参数
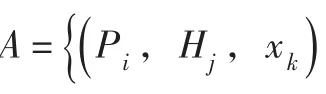
(2)机组发电工况细分,根据国标GB/T 32584-2016中水电机组稳态运行工况的定义,要求机组流量(有功)、水头等主要参数保持在±1.5%以内[15]。可将水头变化范围△H在3%以内、负荷变化范围△P在3%以内的所有工况近似为相同工况。据此,机组发电工况可细分成以下若干典型工况:
(1.5%,91.5%)、(4.5%,91.5%)、…、(118.5%,91.5%)
(1.5%,94.5%)、(4.5%,94.5%)、…、(118.5%,94.5%)
......
(1.5%,137.5%)、(4.5%,137.5%)、…、(118.5%,137.5%)
说明:如(1.5%,91.5%)代表所有有功功率/额定功率在0~3%、水头/额定水头在90%~93%范围内的发电工况。
(3)各个典型工况振动的健康区间计算,下面以典型工况(94.5%,91.5%)的上导X摆度为例,说明振动健康区间的计算方法,其他工况和测点的计算方法类似。
本实例数据来自试验样本,试验在相对功率为94.5%、相对水头为91.5%附近的工况下进行,并选取30个上导X摆度的样本数据得到:{180,182,179,193,174,168,192,191,172,194,196,165,190,183, 182, 190,187,170,189,187,173,178, 188,178,184,196,177,204,179,173}。
因此上导X摆度的正常区间取整后为[154,210]。
典型工况(94.5%,91.5%)上导X摆度的下限记录表示为(94.5%,91.5%,154),上导X摆度的上限记录表示为(94.5%,91.5%,210)。
重复第上述步骤,可得到其他典型工况( )Pi,Hj的上导X摆度下限记录和上限记录,记为和。
以数值预警模型中振动记录的有功参数为X轴、水头参数为Y轴、摆度值为Z轴在三维坐标系中进行绘图,将所有点连成一个曲面,可得到上导摆度的下限预警曲面和上限预警曲面,从而建立水电机组上导X摆度的可视化预警模型图。图3为研究机组上导X摆度的三维可视化预警上限面。
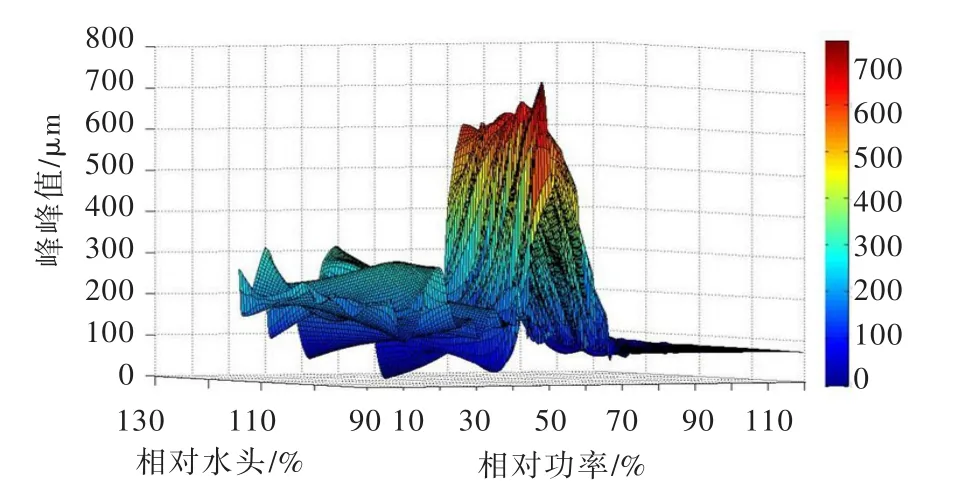
图3 上导X摆度三维可视化预警上限曲面
4.2 预警模型的应用对该机组已安装的稳定性监测系统,进行功能扩展,增加预警模型,组成水电机组振动监测及劣化预警系统,系统工作流程见图4。通过在线监测可以获得机组当前振动值、有功和水头参数等,同时在数值预警模型中可检索到对应的振动上限值和下限值,若振动实测值不在振动上限与下限之间则发出预警信息,实现振动状态的劣化预警。
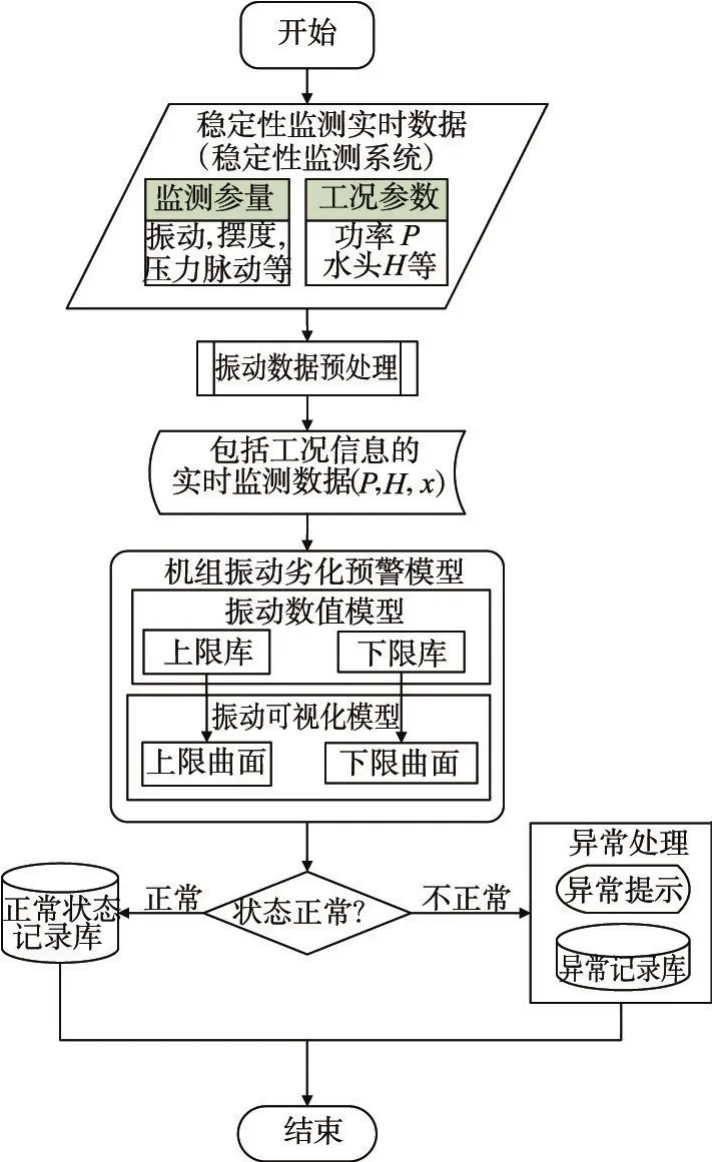
图4 振动监测及劣化预警系统工作流程
预警结果为正常则将振动实时数据记录存入振动正常记录库;预警结果为异常则将振动实时数据记录存入振动异常记录库,以便于进一步的故障诊断、分析查找原因。
预警模型运行一定时期后或者机组大修后,机组运行状态会发生较大变化。为了使得模型能更精确反映机组实际情况,可以采取手动或定期自动的方式,读取正常状态记录,求取各个典型工况的健康区间,重建数值预警模型和可视化预警模型,实现模型的自我完善,使得预警模型全面、准确反映机组振动状态,提高预警结果的精度。
4.3 预警结果分析图5是机组稳定运行工况时上导X摆度可视化预警结果,图中机组摆度位于上限预警曲面下方、下限预警曲面的上方,摆度状态正常;此时机组实测摆度值为175 μm,机组当前相对功率98%、相对水头106%,查询数值预警模型得到该工况下机组的预警区间为[158,235],机组实测摆度落在该工况预警区间内,摆度状态正常。
图6是机组部分负荷运行时上导X摆度可视化预警结果,图中机组摆度位于上限预警曲面下方、下限预警曲面的上方,机组摆度状态正常;此时机组实测摆度值为552 μm,机组当前相对功率60%、相对水头115%,查询数值预警模型得到该工况下机组的预警区间为[461,623],机组实测摆度落在该工况预警区间内,摆度状态正常。
图7是该机组摆度传统预警分析法的分析结果。图中350 μm水平线为摆度预警线,预警值的确定主要参考国标GB/T 11348。从图中可以看出该机组在不同水头、不同负荷下的摆度存在较大的差异性;在80%~120%负荷范围内各水头下机组摆度未超过预警值;而各水头80%负荷以下,机组摆度大都超过350 μm预警线,然而这并不意味着机组摆度异常,而是机组部分负荷的稳定性特性决定的,因此传统预警法仅适合机组稳定运行区域,不能用于机组部分负荷区运行时的预警。
预警结果分析表明:振动劣化预警模型对机组稳定工况和部分负荷工况均能有效预警,且具有自学习功能,预警准确性高;而传统预警法预警限值单一、只能对机组稳定运行工况进行预警保护,预警限值不具备自学习能力。
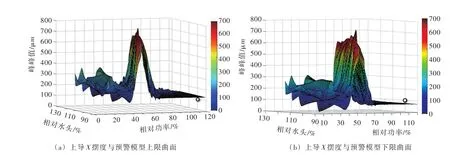
图5 机组稳定运行区时上导X摆度的可视化预警结果(相对功率98%、相对水头106%、上导X摆度175 μm)
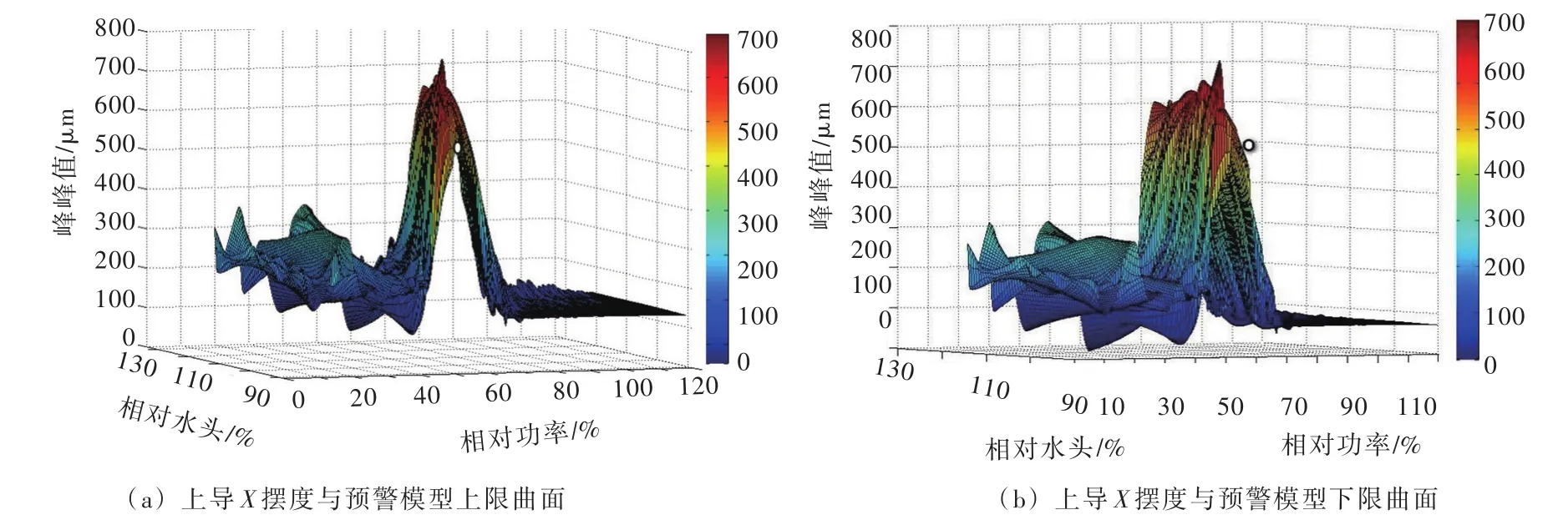
图6 机组部分负荷运行区时上导X摆度可视化预警结果(相对功率60%、相对水头115%、上导X摆度552 μm)
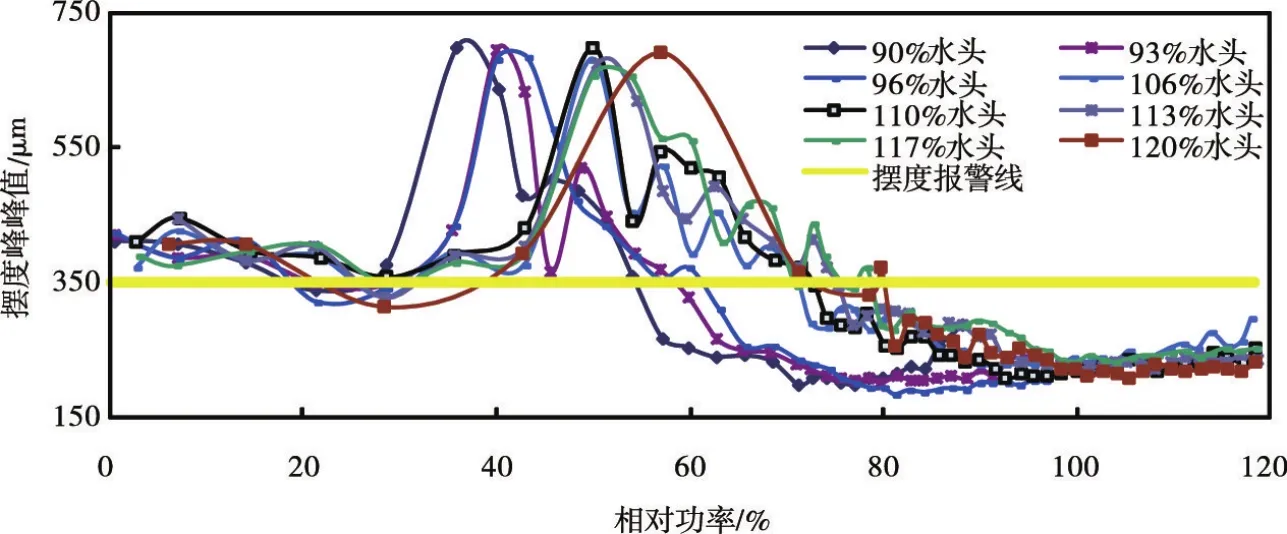
图7 不同水头下上导X摆度的传统预警结果
5 结论
本文提出了水电振动劣化预警模型,利用机组健康状态下的样本数据,建立不同水头和负荷参数下的振动健康区间,实现了机组振动状态的异常预警。本文通过理论分析和实例证明得到以下结论:(1)相近工况下的机组振动混频幅值符合正态分布规律。(2)振动预警模型可提前预警水电机组的振动劣化,为防止水电设备故障提供了新的有效方法。(3)与传统预警方法比较,振动劣化预警模型适用工况范围广、预警结果更加精准。(4)振动劣化预警模型具有自学习功能,提高了模型的适用性,可有效避免渐变性振动故障的发生。
[1]安学利,潘罗平,张飞,等.水电机组劣化趋势混合预测模型[J].水力发电学报,2014,33(3):286-291,310.
[2]付文龙,周建中,张勇传,等.基于OVMD与SVR的水电机组振动趋势预测[J].振动与冲击,2016,35(8):36-40.
[3]钱冰,邹磊,马越 .设备故障早期预警系统在水电机组检修中的应用[J].人民长江,2014,45(17):48-51.
[4]NENNEMANN B,PARKINSON É .YiXing pump turbine guide vane vibrations:Problem resolution with ad⁃vanced CFD analysis[C]//25th IAHR Symposium on Hydraulic Machinery and Systems.2010.
[5]尹铫,刘碧龙,常道庆,等.张河湾蓄能电站厂房噪声与振动调查[J].噪声与振动控制,2012,10(S1):157-160.
[6]徐永,李朝晖.基于仿真模型的水电机组振动特性分析[J].水力发电学报,2013,32(3):247-251,264.
[7]赵志宏,杨绍普,申永军.基于独立分量分析与相关系数的机械故障特征提取[J].振动与冲击,2013,32(6):67-72.
[8]郭谋发,徐丽兰,缪希仁,等.采用时频矩阵奇异值分解的配电开关振动信号特征量提取方法[J].中国电机工程学报,2014,34(28):4990-4997.
[9]EDUARD E,CARME V,DAVID V,et al.Condition monitoring of pump-turbines:New challenge[J].Messure⁃ment,2015,67:151-163.
[10]张飞,潘罗平,安学利.水轮发电机组稳定性参数统计特性与监测报警阈值研究[J].水力发电学报,2013,32(5):269-272,293.
[11]安学利,潘罗平,桂中华,等.抽水蓄能电站机组异常状态检测模型研究[J].水电能源科学,2013,31(1):157-160.
[12]贾嵘,李涛涛,夏洲,等.基于随机共振和经验模态分解的水力发电机组振动故障诊断[J].水利学报,2017,48(3):334-340,350.
[13]党建,何洋洋,贾嵘,等.水轮发电机组非平稳振动信号的检测与故障诊断[J].水利学报,2016,47(2):173-179.
[14]中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.GB/T 11348-2008,旋转机械转轴径向振动的测量和评定第5部分:水力发电厂和泵站机组[S].北京:中国标准出版社,2008.
[15]中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.GB/T 32584-2016,水力发电厂和蓄能泵站机组机械振动的评定[S].北京:中国标准出版社,2016.

