怒江上游流域降雪识别及其演变趋势和原因分析
刘少华 ,严登华 ,王 浩 ,秦天玲 ,翁白莎 ,卢亚静
(1.流域水循环模拟与调控国家重点实验室,北京 100038;2.中国水利水电科学研究院 水资源研究所,北京 100038;3.长江勘测规划设计研究院,湖北 武汉 430010)
1 研究背景
降水是水循环过程中最活跃的要素,其相态变化直接影响地表能量和水循环过程[1-2]。降雪在地表的累积不仅增加了地表反射率,改变了地表的能量过程;而且延迟了产汇流时间,改变水循环过程[3-4]。青藏高原是气候变化的敏感区,典型的高寒气候使得其降雪量在降水中占据了较大的比例,在以增温为背景的气候变化作用下其降雪时空分布均发生了显著变化,进而改变了融雪过程的时空特征,对其水循环过程产生了深刻的影响[5]。
当前基于降水形成机理的相态识别研究以气象学研究为主,即以大气层温度廓线为基础,根据大气层温度及厚度的梯度变化识别降水过程中的相态变化[6-8]。如许爱华等[9]对2005年我国的一次寒潮事件研究表明,925 hPa气温<-2℃则可作为降雪的预报判据。李江波等[10]对2007年河北地区一次春季强寒潮研究指出:0℃层高度低于950 hPa、1000 hPa温度<2℃且925 hPa温度<-2℃时,降雨转变为降雪或者雨夹雪;高洋等[11]对2008年我国南方地区的冻雨过程研究指出,700 hPa附近温度最高达到4℃以上,有利于形成降雨;在850 hPa以下气温明显<0℃,有利形成降雪。然而,由于气象系统的复杂性和大气层相关资料的稀缺性,以及气象学与水文学研究时空尺度的差异性,基于气象学研究的降雪识别尚难以应用于水循环研究。水文学研究中通常采用统计学方法对降水相态进行识别,常用方法可分为以下两种:(1)单温度阈值法,当气温高于临界温度时认为降水以液态(降雨)发生,当气温低于临界温度是认为降水以固态(降雪)发生[12];(2)双温度阈值法,当气温高于临界高温时认为降雨概率是100%,当气温低于临界低温时则认为降雪概率是100%,当气温介于临界温度之间时认为降雪概率随温度呈线性变化[13-14],或根据临界温度区间降雪事件与气温的统计关系确定降雪事件发生概率[15-2]。由于不同区域气候条件和下垫面系统的差异性,单温度阈值难以适应不同区域的气候特征,加之降水过程受局部环境影响显著,单温度阈值降雪识别必然会导致较大误差[16]。双温度阈值法在当前降雪识别研究中应用较广泛,相关学者根据其研究区域的气候特征提出了多种双温度阈值法,其中指数方程形式的双温度阈值法在青藏高原地区的降雪识别中精度较高[17]。
本文选取青藏高原东部的怒江上游流域为研究区域,以流域气象站点观测气温和降水相态资料为基础,采用指数方程形式的双温度阈值方法进行流域降雪的识别、验证及趋势分析,并通过设置气温和降水的控制情景方案,量化识别气温和降水的变化对流域降雪量变化的贡献。
2 研究区概况及数据
2.1 研究区概况怒江上游流域位于青藏高原东南部,流域界于东经91°10′—96°20′和北纬29°55′—32°50′之间、面积约76 000 km2、平均海拔在4 000 m以上。流域大部分区域属高原亚寒带季风湿润与半湿润气候区,多年平均日气温为0.26℃,月平均气温从11月至次年3月均在0℃以下。流域多年平均降水量556 mm,其中80%的降水量集中在6—9月,多年平均降雪量不足降水总量的20%,但由于流域内积雪分布广泛,积雪融水是流域春季径流的重要组成部分,且在温升作用下发生了显著的变化。识别怒江上游流域降雪过程,量化气候变化对降雪量的影响,对于提高积雪融水模拟精度、明晰径流的年内分配特征、支撑变化环境下流域水资源综合管理具有重要意义。
2.2 数据资料我国公开降水相态资料相对匮乏,由国家气象信息中心提供的日降水资料集(V3.0)中仅1979年以前降水资料中标记了降水相态(降雨/降雪/雨夹雪)。怒江上游流域气象站点稀疏,是典型的缺资料地区[18],流域内部及周边仅有6个气象站具有降水相态记载(图1),统计各气象站点年均气温、降水量以及降水相变的临界气温(根据每0.5℃区间气温与降雪比例关系得到)见表1。由于单个站点系列较短、样本代表性差,研究综合流域6个气象站的1979年以前逐日降水相态和平均气温资料,统计临界气温内(-4~8℃)气温与降雪比例关系,并拟合得到流域降雪识别指数方程。
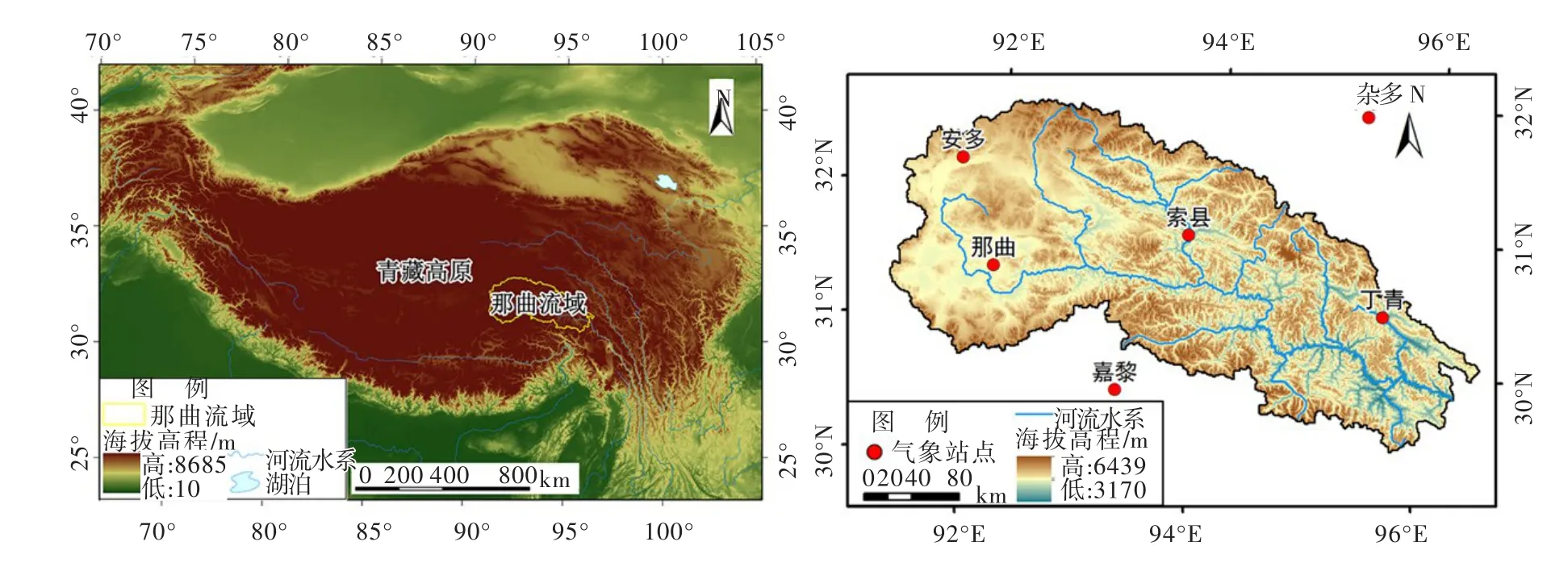
图1 怒江上游流域位置及气象站点分布
3 研究方法
3.1 降雪量识别方法气象站点的降水相态标记资料中无法得知雨夹雪中降雪的含量,统计研究区气象站点不同气温下降雪量占降雪和降水总量的比值(不考虑雨夹雪情况下的气温与降雪比例关系),绘制其降雪比例与日平均气温的关系(图2(a))。当温度小于临界低温(Tmin)时,降水完全以降雪形态发生;当温度大于临界高温(Tmax)时,降水完全以降雨形态发生;临界温度内(Tmin~Tmax),降雪比例与日平均气温成指数函数关系[2-17],可概化为如下方程:

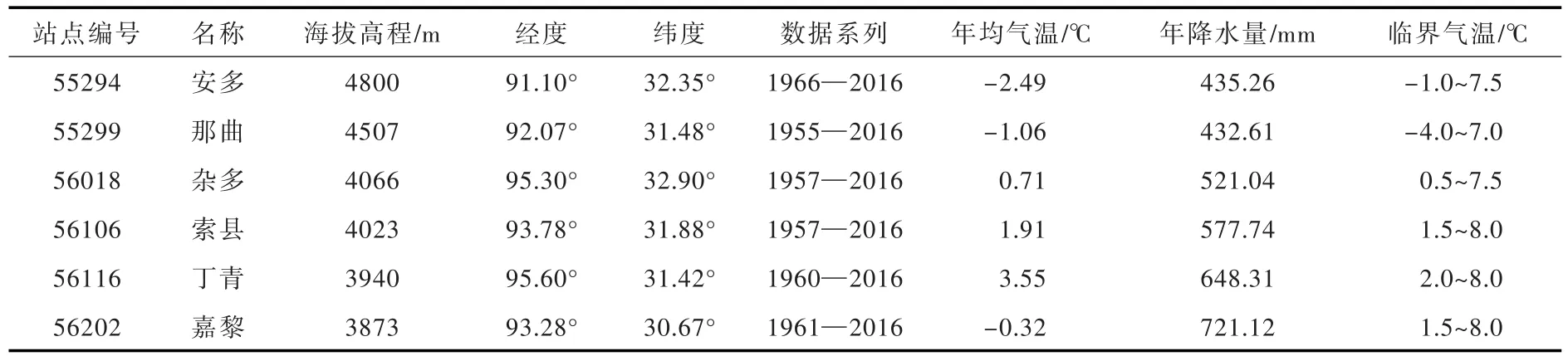
表1 气象站点相关信息
式中:PS为降雪比例;T为日平均气温;a和b均为指数方程的经验参数,可以根据研究区域气温与降雪比例的统计关系采用最小二乘法估算得到。
在此基础上,假定相同温度下雨夹雪中降雪比例也满足该指数方程,并统计研究区域不同气温下降雪量、雨夹雪和降雨量占总降水量的比值,绘制降水各相态与日平均气温的关系(图2(b))。进而,把各气象站点雨夹雪中估计降雪量和观测降雪量之和作为其总降雪量,并以此为据验证采用指数方程识别总降水量得到的降雪量。
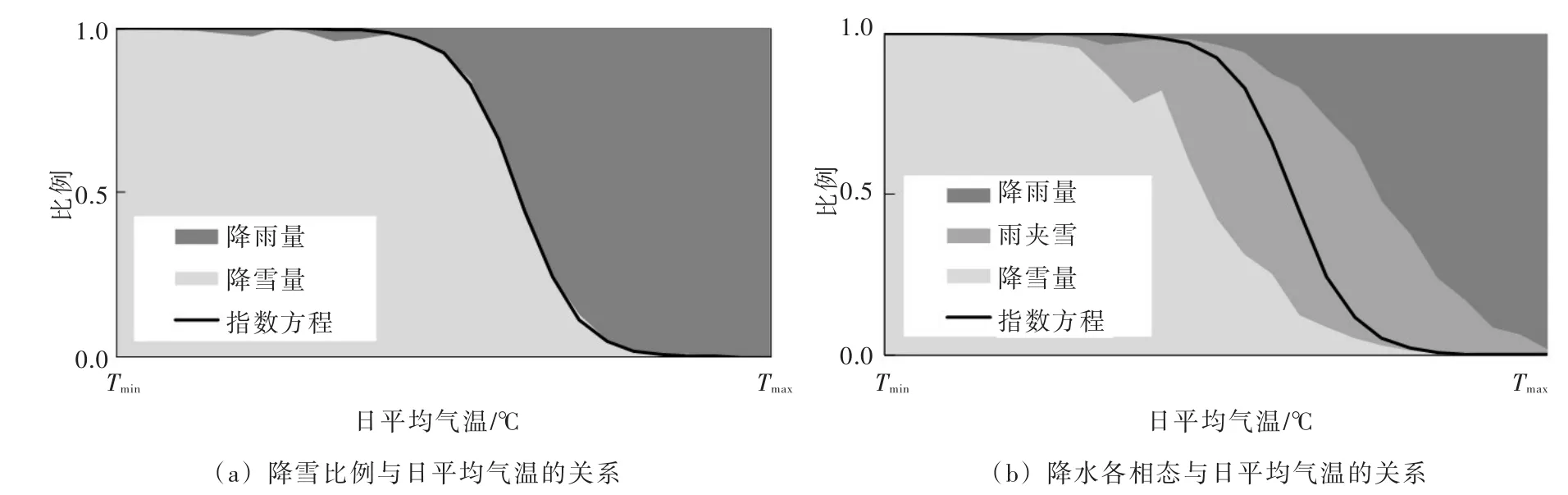
图2 降水各相态比例与气温关系
3.2 降雪量变化趋势检验根据各气象站点逐日气温和降水量,采用指数方程识别其逐日降雪量,并累计得到其年降雪量过程。通过线性回归分析各气象站点年平均气温、年降水量和年降雪量变化趋势,并采用Mann-Kendall检验法对其变化趋势进行显著性检验。Mann-Kendall检验法是气象水文分析中最常用的一种非参数检验方法[19],其计算公式如下:
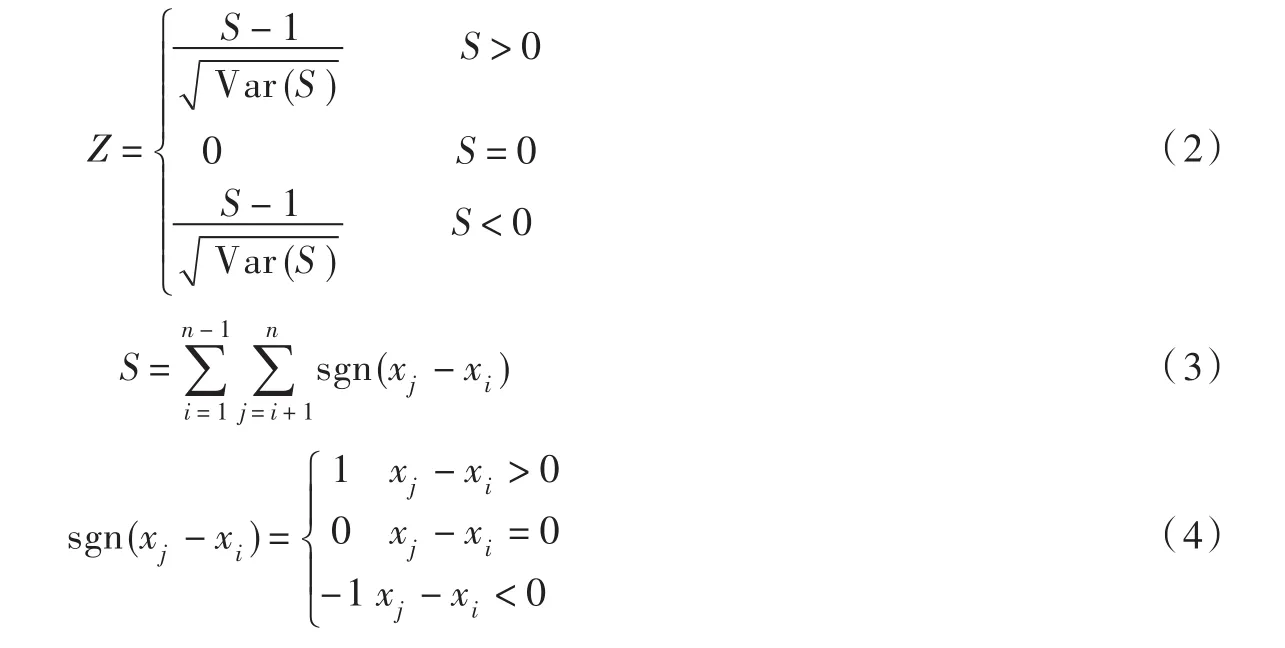

式中:x为进行趋势检验的时间序列;n为时间序列的长度。统计量Z符合正态分布,在给定的α置信水平上,当,则拒绝零假设,表明该时间序列的变化趋势满足显著性检验;Z>0,表明序列具有上升趋势,反之为下降趋势。
3.3 气温和降水对降雪量影响的分解降雪是降水在一定气候条件下的特殊形态,降雪量的变化是降水量变化的直接体现,但同时也受到以增温为主导的气候变化的影响。为了量化气候变化背景下气温和降水的变化对降雪量变化的贡献,根据研究区域气候变化的突变点把其气候要素时间序列划分为两个阶段:气候变化前和气候变化后,并以气候变化前多年平均降雪量作为基准值(S0),以气候变化后多年平均降雪量作为气候变化后降雪量(SC)。同时,设置不同气温和降水量控制方案,分别研究气温和降水量变化对降雪量变化的贡献。
(1)气温控制方案。对气候变化后逐日平均气温去趋势化修正得到无趋势逐日平均气温系列。具体步骤:①计算得到气候变化后年平均气温的增长速率;②根据年逐日平均气温减去该年平均气温增量(年平均气温增长率乘以年序号),得到相应年份去趋势化逐日气温系列。根据去趋势化逐日平均气温和降水量,重新应用指数方程对气候变化后逐日降雪量进行估计,得到控制气温条件下多年平均降雪量(ST)。
(2)降水控制方案。由于指数方程可知,当温度不变时降水中降雪的比例是定值,即统计意义上温度不变降雪率(降雪量/降水量)相同。根据气候变化后多年平均降雪率乘以气候变化前多年平均降水量得到控制降水条件下多年平均降雪量(SP)。根据以上控制条件的降雪量,可分别得到气温、降水量以及两者共同影响对降雪量变化的贡献率:
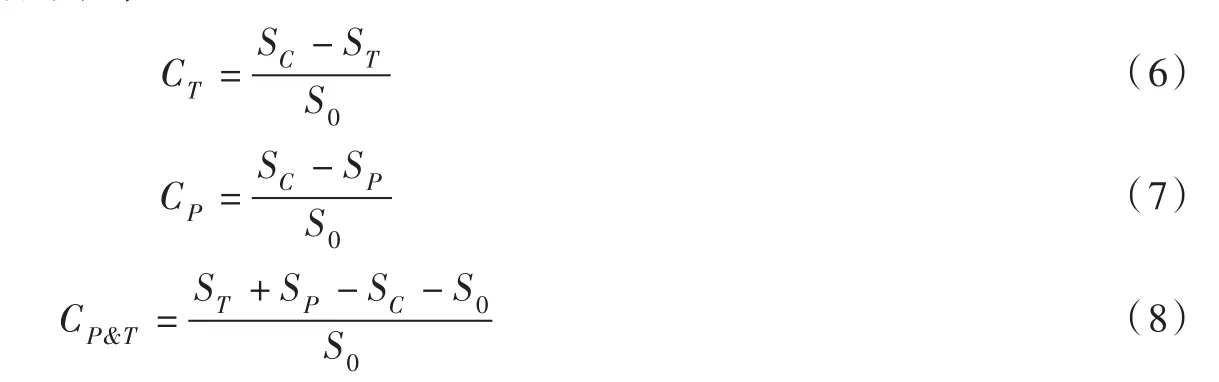
其中,CT、CP和CP&T分别是气温、降水以及两者共同影响对降雪量变化的贡献率,需要注意的是此处贡献率是指由于气温和降水的改变导致的降雪变化率(相对于气候变化前多年平均降雪量S0),所以其理论取值范围为[-1,+∞)(负值表示该要素的增加/升高对降雪量的增加具有负贡献),一般情况下三者之和不为1。
4 案例应用
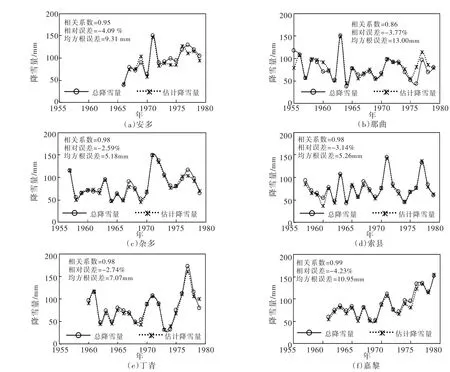
图3 各气象站点总降雪量与估计年降雪量
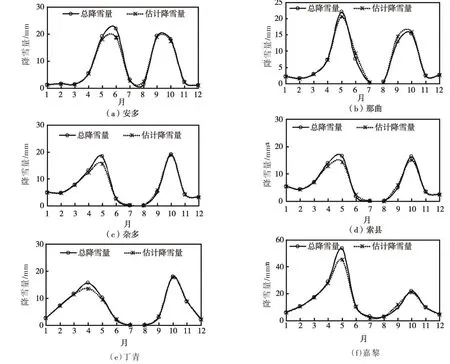
图4 各气象站点多年月总降雪量与估计月降雪量
4.1 降雪量的识别及验证综合怒江上游流域6个气象站点1979年以前气温和降水相态资料,统计其气温与降雪比例关系,采用指数方程对其进行拟合,以流域临界气温范围(-4~8℃)作为拟合区间,拟合计算步长为0.5℃。根据最小二乘法估算拟合指数方程参数a和b的值分别为-6.11和1.81,残差平方和为0.0038。通过指数方程估计流域各气象站点1979年以前逐日降雪量,并统计其历年估计降雪量与总降雪量关系(图3)可知:除那曲站外各气象站点估计年降雪量相关系数均在0.95以上,那曲站估计年降雪量相关系数略低,但仍表现出与总降雪量较好的一致性。各气象站点估计年降雪量的累计相对误差范围均在5%以内,仅那曲站相对误差为正值。其原因是流域临界气温与气象站点实际临界气温存在一定偏差:流域临界气温较那曲站临界气温偏高(指数方程向右便移),导致那曲站估计降雪量偏高;相反,流域临界气温较其他站点临界气温偏低(指数方程向左偏移),导致其估计降雪量偏低。总体而言,该降雪识别方法可能低估怒江上游流域降雪量,但整体能够较好的估计各气象站点的年降雪量。其次,统计气象站点各月多年平均估计降雪量(图4)显示,各气象站点降雪量主要集中在春夏(4—6月)和夏秋交替月份(9—10月),其原因是怒江上游流域春季和冬季降水量较少、夏季气温较高,不利于形成降雪。而春夏和夏秋交替月份具有一定规模的降水量,且其平均气温均在临界温度内,容易形成降雪。春夏交替季节各气象站点降雪量出现的峰值从流域东南向西北具有一定滞后现象,其中丁青站降雪峰值出现最早在4月份,安多站降雪峰值出现最晚在6月份,其他站点降雪峰值均出现在5月份,且降雪峰值月份的估计降雪量明显偏低。其可能原因是怒江上游流域春夏交替季节,伴随气温升高季风携带大量水汽由东南向西北快速推进,使得流域西北部雨季较东南部滞后;同时,高海拔地形作用下该月份冷暖气流交汇频繁易形成区域短历时降雪,该降雪过程受气温影响较小[20],导致基于气温和降雪比例统计关系的指数方程普遍低估流域降雪量。
4.2 降雪量演变趋势分析降雪是大气在一定的湿度、温度以及区域环流场等综合条件下形成的固态降水,其形成条件虽复杂多样,但并不随气象要素演变而变化。根据气温和降雪比例统计关系拟合得到的降雪识别指数方程则是对降雪形成条件的定量概化。因而,可根据流域气象站点1979年以前资料获得的流域降雪识别指数方程对各气象站点1980—2016年逐日降雪量进行识别,并采用线性回归分析1979年前后各气象站点年平均气温、年降水量、年降雪量变化趋势(图5)。结果可知:流域整体上气温呈升高趋势,且1979年以后气温升高趋势更为明显;1979年以前流域整体降水量变化趋势不明显,各气象站点降水趋势不完全一致,1979年以后安多和杂多站降水量呈减少趋势,其余气象站点的降水量均呈现出增加趋势。与此同时,1979年以前流域降雪量呈增加趋势,仅那曲站降雪量表现出微弱的减少趋势,1979年以后所有气象站点降雪量均表现出减少趋势。根据Mann-Kendall趋势检验结果(表2)可知,各气象站点1980—2016年平均气温、年降水量和年降雪量的变化趋势与线性回归趋势基本一致,其中平均气温均呈显著增加趋势,但降水量和降雪量变化趋势均不显著。

表2 各气象站点年1980—2016年均气温、年降水量和年降雪量变化趋势的显著性检验结果(Z值)
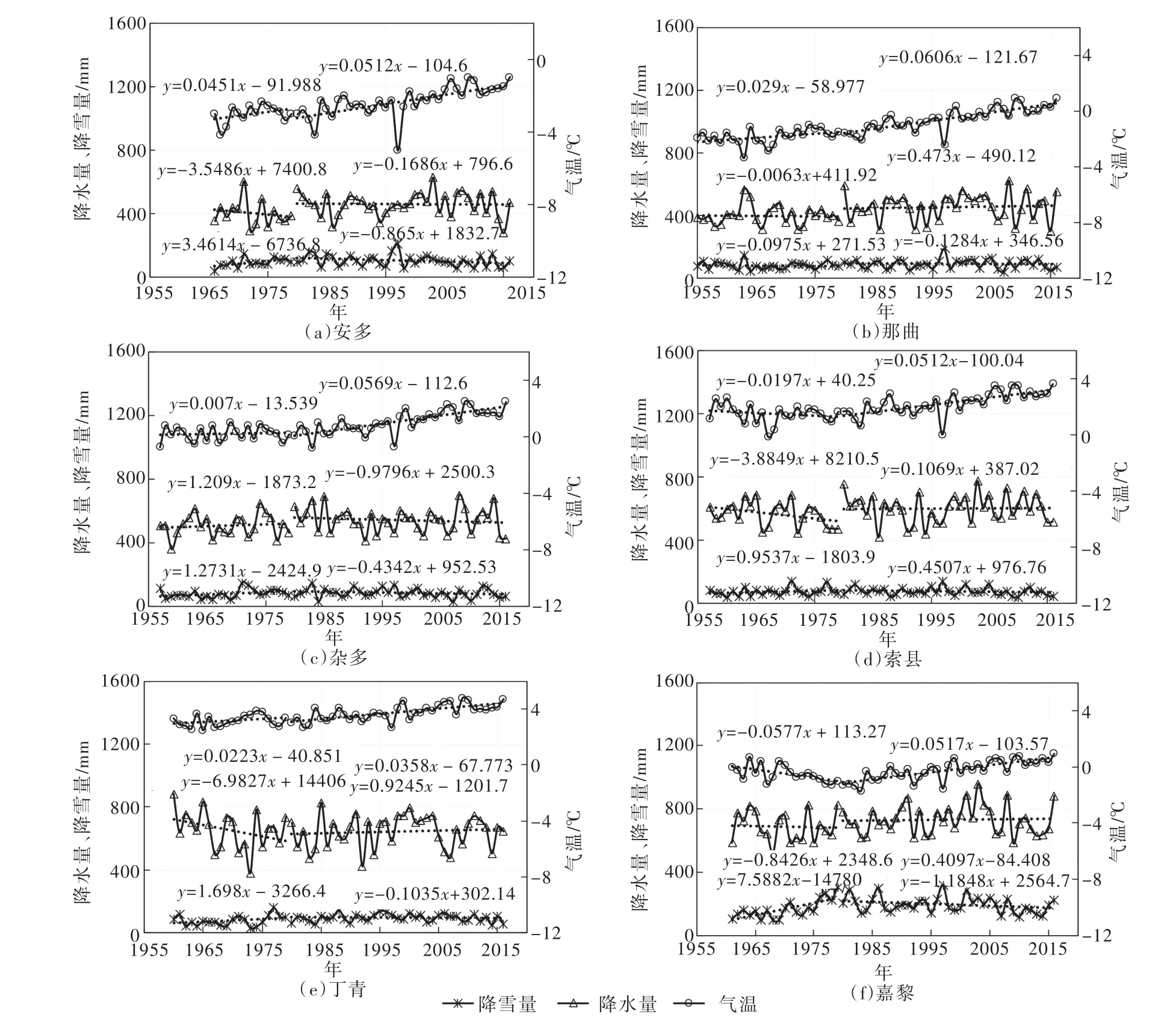
图5 各气象站点估计年降雪量、年平均气温和年降水量变化趋势
4.3 气温和降水对降雪量影响分析研究采用现有研究普遍认可的1980年作为怒江上游流域气候变化的转折点[21-24],采用已获得的流域降雪指数识别方程,对气象站点1980年后不同控制方案下的多年平均降雪量进行估计,并量化识别气候变化后流域气象站点气温和降水变化对降雪量变化的贡献率(图6),结果表明:各气象站点1979年以后多年平均降雪量较之前多年平均降雪量均有所增加。各气象站点气温升高对于降雪量表现出明显的减少作用。除丁青站外其他气象站点1979年以后多年平均降水量均大于之前,并对其降雪量具有明显的增加作用。丁青站1979年以后多年平均降水量略低于之前,因而其对降雪量呈现出了减少作用。怒江上游流域气温和降水对降雪量的影响呈东南向西北方向逐渐增强分布规律,其可能原因是流域的平均气温和年降水量均呈西南向东北递减分布特征,气温越低、降水量越少降雪量对气温和降水变化的响应越敏感。气温和降水量共同影响对各气象站点降雪量均表现出增加作用。原因是气候变化背景下流域低温条件下降水概率增加(图7),对于各气象站点降雪量增加具有显著促进作用。
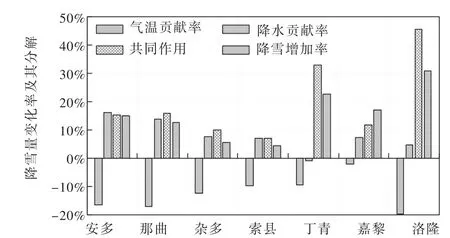
图6 各气象站点1979年以后多年平均降雪量增加率及其分解

图7 1979年前后降水随气温变化的概率分布
5 结语
(1)基于降雪比例和日平均气温的降雪识别指数方程,能够在年和月尺度上较好估计怒江上游流域各气象站点降雪量。各气象站点估计降雪量与总降雪量相关系数均在0.86以上,相对误差均在5%以内。
(2)1979年以后,怒江上游流域各气象站点气温均呈显著增加趋势,各气象站点降水量和降雪量变化趋势并不一致,流域整体上年降水量和年降雪量分别呈增加和减少趋势,但趋势并不显著。
(3)怒江上游流域气象站点气温升高具有减少降雪量的作用,且作用强度从流域东南向西北逐渐增强。气候变化背景下,低温条件下降水概率增加对各气象站点的降雪量的增加具有显著促进作用,但1979年以后气温的显著增加对降雪量的影响占据主导作用,使得流域降雪量整体呈减少趋势。
[1]LOTH B,GRAF H F,OBERHUBER J M.Snow cover model for global climate simulations[J].Journal of Geo⁃physical Research:Atmospheres,1993,98(D6):10451-10464 .
[2]DING B,YANG K,QIN J,et al.The dependence of precipitation types on surface elevation and meteorological conditions and its parameterization[J].Journal of Hydrology,2014,513(11):154-163 .
[3]CLARK M P,SLATER A G,BARRETT A P,et al.Assimilation of snow covered area information into hydrologic and land-surface models[J].Advances in Water Resources,2006,29(8):1209-1221 .
[4]BOX J,FETTWEIS X,STROEVE J,et al.Greenland ice sheet albedo feedback:thermodynamics and atmospher⁃ic drivers[J].The Cryosphere,2012,6(4):821-839 .
[5]姚檀栋,秦大河,沈永平,等.青藏高原冰冻圈变化及其对区域水循环和生态条件的影响[J].自然杂志,2013,35(3):179-186 .
[6]漆梁波,张瑛.中国东部地区冬季降水相态的识别判据研究[J].气象,2012,38(1):96-102.
[7]张琳娜,郭锐,曾剑,等 .北京地区冬季降水相态的识别判据研究[J].高原气象,2013,32(6):1780-1786.
[8]徐辉,宗志平 .一次降水相态转换过程中温度垂直结构特征分析[J].高原气象,2014,33(5):1272-1280.
[9]许爱华,乔林,詹丰兴,等.2005年3月一次寒潮天气过程的诊断分析[J].气象,2006,32(3):49-55.
[10]李江波,李根娥,裴雨杰,等 .一次春季强寒潮的降水相态变化分析[J].气象,2009,35(7):87-94.
[11]高洋,吴统文,陈葆德.2008年1月我国南方冻雨过程的热力异常及其形成原因[J].高原气象,2011,30(6):1526-1533.
[12]YANG Z L,DICKINSON R E,ROBOCK A,et al.Validation of the snow submodel of the biosphere-atmosphere transfer scheme with Russian snow cover and meteorological observational data[J].Journal of Climate,1997,10(2):353-373.
[13]WIGMOSTA M S,VAIL L W,LETTENMAIER D Pv.A distributed hydrology-vegetation model for complex ter⁃rain[J].Water Resources Research,1994,30(6):1665-1679 .
[14]CHEN R,LU S,KANG E,et al.A distributed water-heat coupled model for mountainous watershed of an inland river basin of Northwest China(I)model structure and equations[J].Environmental Geology,2008,53(6):1299-1309.
[15]DAI A.Temperature and pressure dependence of the rain-snow phase transition over land and ocean[J].Geo⁃physical Research Letters,2008,35(12):62-77 .
[16]韩春坛,陈仁升,刘俊峰,等.固液态降水分离方法探讨[J].冰川冻土,2010,32(2):249-256.
[17]LIU S,YAN D,QIN T,et al.Precipitation phase separation schemes in the Naqu River basin,eastern Tibetan plateau[J].Theoretical&Applied Climatology,2016.doi:10.1007/s00704-016-1967-7 .
[18]刘昌明,白鹏,王中根,等 .稀缺资料流域水文计算若干研究:以青藏高原为例[J].水利学报,2016,47(3):272-282.
[19]刘少华,严登华,翁白莎,等 .近50a中国≥10℃有效积温时空演变[J].干旱区研究,2013,30(4):689-696.
[20]徐祥德,陶诗言,王继志,等.青藏高原-季风水汽输送“大三角扇型”影响域特征与中国区域旱涝异常的关系[J].气象学报,2002,60(3):257-266.
[21]冯新灵,罗隆诚,冯自立.中国近50年降水变化趋势及突变的Hurst指数试验[J].干旱区地理,2009,32(6):859-866.
[22]尹云鹤,吴绍洪,陈刚.1961—2006年我国气候变化趋势与突变的区域差异[J].自然资源学报,2009,24(12):2147-2157.
[23]刘春蓁,占车生,夏军,等.关于气候变化与人类活动对径流影响研究的评述[J].水利学报,2014,45(4):379-393.
[24]朱丽华,范广洲,华维.全球变暖背景下青藏高原夏季气温在对流层上下反相变化及其与降水和环流的关系[J].大气科学,2015,39(6):1250-1262.

