基于Copula函数的导弹多性能退化可靠性评估

戴宗亮， 李小兵， 王慧杰

(空军工程大学 防空反导学院，陕西 西安 710051)

0 引 言

导弹在整个寿命周期中，绝大部分时间处于贮存状态[1]。在长期贮存过程中，导弹必然会受到周围各种环境应力的影响，难免引起设备性能参数的变化，导致整个系统功能异常或可靠度降低[2]，目前，常用的解决多性能退化参数可靠性评估的方法有2种: 1)假设多个性能参数之间相互独立，可以按照串联系统的方法进行处理，具有简单快速的优点，但分析不够全面，评估结果误差较大; 2)充分考虑性能参数之间的相关性，如联合概率密度法和状态空间法[3,4]，优点是充分考虑了参数之间的相关性，但在特征参数较多时存在计算量大和建模困难。Copula函数[5,6]作为一种灵活、稳健的相关性分析函数，在分析变量间相关性时具有诸多的优点。

本文提出了基于Copula函数的多性能退化可靠性评估模型。

1 多性能参数退化数据可靠性模型

根据导弹的退化机理[7]，导弹性能的退化是m个退化参数直接影响的结果，其可靠度为

R(t)=P{Y1(t)≤D1,Y2(t)≤D2,…,Ym(t)≤Dm}

ym(t)dy1dy2…dym

(1)

式中f(y1(t),y2(t),…,ym(t))为y1(t),y2(t),…,ym(t)的联合概率分布。由式(1)可知，只要知道联合概率密度函数f(y1(t),y2(t),…,ym(t))，根据已知的失效阈值，即可求得多退化模型的可靠度R(t)。要知道这些性能参数在统计学上的相关性，通常可以通过性能参数间的协方差运算获得其相关性。其方差—协方差矩阵可表示为

(2)

当cov(yi(t),yj(t))=0，表示第i和第j个性能参数独立,i,j=1,2,…,m。当V的非对角线元素均为零，则可认为产品性能参数均相对独立，可将其等效成串联系统，可靠度为

R(t)=P{Y1(t)≤D1,Y2(t)≤D2,…，Ym(t)≤Dm}

=P{Y1(t)≤D1}·P1{Y2(t)≤D2}·…·

(3)

当V的非对角线元素非全零，则可认为产品性能参数不全相对独立，则要求出其联合概率密度函数f(y1(t),y2(t),…,ym(t))，以此求得可靠度。因此，建立多性能参数产品的可靠性模型的关键是建立求取各性能参数的联合概率密度函数f(y1(t),y2(t),…,ym(t))。

如果性能参数退化量Y1(t),Y2(t),…,Ym(t)的边缘分布均服从为正态分布，则多性能参数产品性能参数退化量的联合分布密度函数为

(4)

式中Y=(Y1(t),Y2(t),…,Ym(t));μ和Σ分别为Y的均值和协方差矩阵。

综上可得，该模型主要有两个难点:联合概率密度f(y1(t),y2(t),…,ym(t))的确定，对于参数边缘分布不同的情况，理论推导其联合分布十分繁琐；在多退化性能相关的条件下，可靠度的计算，协方差矩阵V的大规模积分计算量较大。

2 基于Copula函数的多性能退化模型

2.1 Copula函数[8]

定义1m维Copula函数是一个定义域为[0,1]m，值域为[0,1]的函数，即函数C：[0,1]m→[0,1]，且满足条件

1)C对于每个变量递增；

2)对[0,1]m中任意uk=0,k≤m，满足C(u1,…,uk,…,um)=0；

3)对[0,1]m中任意vk∈[0,1],k≤m，满足C(1,1,…vk,…,1,1)=vk；

4)对[0,1]m中所有的ak,bk∈[0,1]m,k=1,2,…,m，且ak≤bk,k=1,2,…,m，有

(5)

对于二元Copula函数，任意u1,u2,v1,v2∈[0,1]，令u1≤u2,v1≤v2，则

C(u2,v2)-C(u1,v2)-C(u2,v1)+C(u1,v1)≥0

(6)

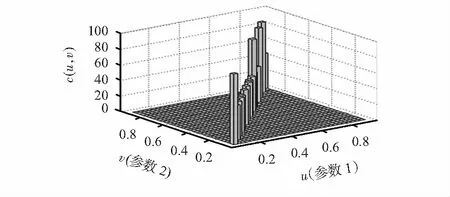
定义2 若∀(u1,u2,…,um)∈Im,C1(u1,u2,…，um)≤C2(u1,u2,…,um)，则称Copula函数C1

m维Copula函数的Freche-hoeffding上、下界分别为

(7)

Sklar定理：一个联合分布函数H(y1,y2,…,ym)可分解为m个边缘分布函数F1(y1),F2(y2),…,Fm(ym)和一个Copula函数，即

H(y1,y2,…,ym)=Cm(F1(y1),F2(y2),…,Fm(ym))

(8)

式中Cm(·)为一个m维的Copula 函数。如果F1(y1),F2(y2),…,Fm(ym)是连续的，则Copula函数唯一确定；否则要根据RandF1×RandF2×…×RandFm确定。相反，如果F1(y1),F2(y2),…,Fm(ym)为分布函数，那么函数H(y1,y2,…,ym)为一个联合分布函数，其边缘分布为F1(y1),F2(y2),…,Fm(ym)，通过Copula函数的密度函数cm(·)和边缘分布函数F1(y1),F2(y2),…,Fm(ym)，可以方便地求出m维分布函数的密度函数如下

h(y1,y2,…,ym)=cm(F1(y1),F2(y2),…,

(9)

2.2 可靠性评估模型

根据Copula函数的理论基础，将Copula函数引入到多性能退化量的可靠性评估模型，不难得出多性能参数产品的联合密度函数为

f(y1,y2,…,ym)=cm(F1(y1),F2(y2),…,

(10)

联合分布函数为

H(y1,y2,…,ym)=Cm(F1(y1),F2(y2),…,Fm(ym))

(11)

假设Ω=(v1,v2,…,vm,θ)为Copula 函数的参数向量，其中v1,v2,…,vm为各个性能参数的边缘分布函数F1(y1),F2(y2),…,Fm(ym)的参数向量，θ为Copula函数的相关系数。根据精确极大似然估计[9]得似然函数为

(12)

将L(Ω)关于参数向量Ω极大化，得极大似然估计为

(13)

式(13)可以同时求得边缘分布函数F1(y1),F2(y2),…,Fm(ym)的参数v1,v2,…,vm和θ，但当维数较高时计算十分复杂，为了简化问题，采用边际分布的函数推断方法(function inference method,FIM)对上式进行参数估计，即二步极大似然估计法。首先利用最大似然估计法对各边缘分布的参数v1,v2,…,vm进行估计，并对参数θ进行估计，其步骤如下：

1)对v1,v2,…,vm进行估计得

(14)

Fm(ymj;vm);θ)

(15)

则可由Copula函数推出产品可靠度为

R(t)=Cm(F1(D1;v1),F2(D2;v2),…,Fm(Dm;vm);θ)

(16)

综上，基于Copula函数的多性能退化模型的步骤为:

1)获取或求取m组数据的边缘分布函数；

2)选择适当的Copula函数形式并求取参数估计值；

3)根据产品可靠度公式求得产品可靠度。

3 实例应用

以某型地空导弹为例，通过MATLAB仿真软件进行仿真计算。已知该型导弹可靠性评定主要由参数X1及参数X2共同决定，在自然条件下连续进行20次测量的数据如表1。

表1 各参数的连续测试数据

其中参数X1的失效阈值为2.5 Ω，参数X2的失效阈值为10 Ω。为确定参数X1,X2的分布类型，首先给出其频率直方图如图1。

从图1难以准确看出参数X1,X2的分布类型，但参数均类似于正态分布，对参数进行正态检验，引入正态分析图对参数进行检验的图2所示。

图1 参数频率直方图

从图2可以看出:参数X1及X2服从正态分布，且求得X1～N(2.2,0.004)，X2～N(42,8)。参数X1及参数X2的二元频率直方图，如图3所示。

图3 X1及X2的二元频率直方图

根据图3及参数X1,X2之间的相关性，选取二元正态Copula[10]作为其连接函数，有

C(u1,u2;ρ)=Φρ(Φ-1(u1),Φ-1(u2))

(17)

C(u1,u2;ρ)=Φρ(Φ-1(u1),Φ-1(u2))=

(18)

将ρl=0.952 3代入式(18)可得各时刻的导弹可靠性数据如图4所示。其随着时间而降低，符合实际规律，同时表明模型的有效性。

图4 导弹各时刻的可靠度

4 结 论

本文提出了基于Copula函数的多性能退化可靠性评估模型，以较高的准确度描述了导弹多性能指标间的关系及系统的可靠性退化特征。模型在确保评估结果准确的基础上，大幅减小了计算量，为导弹多性能退化可靠性模型研究提供了一种新方法，具有较高的推广性和实用性。

[1] QJ3153—2002.导弹贮存可靠性设计技术指南[S].

[2] 段鹏程,王学奇,霍建成,等.基于多传感器的机载导弹环境应力监测装置[J].传感器与微系统,2015,34(9):111-114.

[3] 曾 健,陈俊芳.Copula函数在风险管理中的应用研究—以上证A股与B股的相关结构分析为例[J].当代财经,2005(2):34-38.

[4] Kim I T,Itoh Y.Accelerated exposure tests as evaluation tool for estimating life of organic coatings on steel bridges[J].Corrosion Engineering,Science and Technology,2007,42(3):242-252.

[5] 刘景森，金 勇.一种基于吉布斯抽样的MUSIC多维参数联合估计算法[J].传感器与微系统,2008,27(6):62-65.

[6] 戴邵武，王克红，钱俭学.基于AKPSO算法的加速度计快速标定方法[J].传感器与微系统,2015,34(2):69-72.

[7] 王 凯.导导弹武器系统贮存环境监测及贮存可靠性评定方法研究[D].哈尔滨:哈尔滨理工大学,2012.

[8] Nelson R B.An introduction to Copulas[M].Berlin Heidelberg:Springer,2006.

[9] 王 琦,冯新喜,杜钦峰.三维传感器极大似然配准算法[J]. 传感器与微系统,2007,26(11):54-56.

[10] 张世英.Copula理论及其在金融分析上的应用[M].北京：清华大学出版社,2008.