线振动MEMS陀螺结构振动非线性特性研究*

苟元东， 王学锋， 庄海涵， 邢朝洋

(北京航天控制仪器研究所，北京 100039)

0 引 言

基于微机电系统(micro-electro-mechanical system,MEMS) 技术的陀螺(MEMS陀螺)，具有小体积、低功耗、易于批量生产、低成本等特点而得到广泛应用。实现高精度的微机械陀螺仪，就必须增大其驱动振幅，从而降低布朗噪声水平和角度随机游走等[4]。但实验结果表明，当驱动振幅超过某个临界值时，陀螺驱动轴将发生非线性迟滞，导致其频率响应曲线发生突变，即陀螺的幅频特性曲线不再连续而出现明显的突变，严重影响了陀螺的稳定性，制约了其性能的提高。目前，针对MEMS谐振器的非线性研究大多集中于定性分析，如振动非线性造成系统谐振频率漂移[5]，导致闭环谐振电路的不稳定性[6,7]，影响闭环自激系统的实现[8]等。但关于谐振器振动非线性系数的测量方法，非线性振动下振幅阈值的计算评估等，国内外鲜有报道。

本文针对一种线振动MEMS陀螺驱动轴的振动非线性问题开展研究，采用理论分析、仿真模拟和实验数据拟合相结合的方法确定模型中的非线性系数，并根据模型推导计算非线性迟滞效应消失点的临界振幅和激励值，为陀螺结构设计提供了理论参考。

1 陀螺驱动轴振动非线性分析

影响MEMS陀螺的非线性因素主要有2方面：机械非线性和电容值非线性。针对电容值非线性，可以通过梳齿变面积设计大幅减小电容值非线性的影响；而微纳米双端固支梁的动态响应却常常表现出明显的非线性特征[9]。因此，本文从谐振梁的角度出发，对线振动MEMS陀螺驱动轴的振动非线性问题开展研究。

1.1 谐振梁刚度非线性理论分析

考虑如图1所示的双端固支梁结构，梁的横向振动导致其中性面的非线性伸长。

根据弹性理论，梁因横向振动而产生的纵向伸长量ΔL为[10]

图1 梁轴向的附加伸长

(1)

式中L为梁的长度；w为梁的横向振动位移；x为梁的纵向位置；t为时间。梁伸长引起梁能量U的变化为

(2)

式中E为梁材料的杨氏模量；A为梁的横截面积。

一般地，梁的横向位移w可以简化成一个与位置x相关的函数β(x)和一个与时间t相关的函数q(t)的乘积，β(x)可取梁的阵型函数。令ε=x/L，将ΔU对当地挠度q(t)进行微分，得到梁的附加轴力Fe

(3)

将谐振梁的尺寸参数代入式(3)，即可以得到梁的非线性刚度系数。

1.2 梁结构有限元仿真

利用有限元建模(finite element modeling,FEM)软件ANSYS计算谐振梁的刚度非线性，其中，谐振梁的尺寸参数设置：梁长为1 938 μm，梁宽为30 μm，梁高为60 μm，杨氏模量为130 GPa，泊松比为0.18。

获得谐振梁的有限元模型，梁两端固支，中心点施加横向驱动力，求解时打开大变形选项，对应不同的驱动力F可以获得相应的梁中点位移x。

为了得到梁的线性和非线性刚度系数，将得到的仿真数据进行多项式拟合[11]

F(x)=k1x+k3x3

(4)

式中F为加载的外力；x为梁中心点的横向位移。

图2为谐振梁仿真结果，根据拟合结果，可以求得谐振梁的刚度非线性系数。

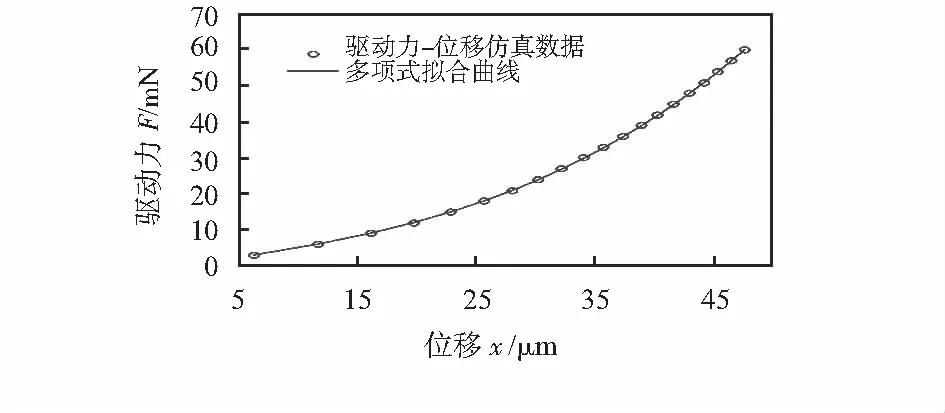
图2 谐振梁驱动力—位移非线性

1.3 陀螺结构FEM仿真

利用有限元软件ANSYS模拟MEMS陀螺结构的刚度非线性，如图3所示。

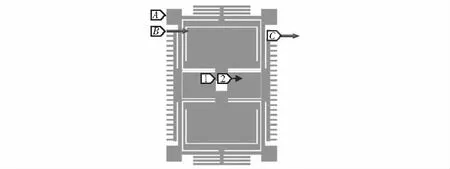
图3 陀螺结构的ANSYS模型简图

图3中，陀螺结构的4个锚点固支，为了更有效地模拟实际情况，将驱动力沿驱动轴方向施加在驱动梳齿上，以陀螺结构中心质量块沿驱动轴方向的偏移量作为位移，求解时打开大变形选项，对应不同的驱动力可以获得相应的位移，将式(4)用于分析结构的刚度非线性，拟合结果如图4。

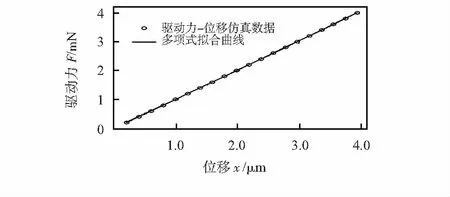
图4 陀螺结构驱动力—位移非线性

将谐振梁的尺寸参数值代入式(3)，得到陀螺驱动轴刚度非线性如表1所示。

表1 梁的非线性刚度

将仿真值分别与理论值相比较，其误差均较小，由此验证了理论计算的正确性。

2 实验对比分析

2.1 非线性系数测定原理

MEMS陀螺的驱动轴可以简化成二阶谐振子系统，引入当陀螺驱动轴方向的等效质量m和等效线性刚度k1时，达芬方程可用于描述陀螺驱动轴方向的非线性动力学特性，则陀螺驱动轴的工作谐振频率可以近似表示为[12]

(5)

式中ω0=k1/m为陀螺驱动轴方向的固有圆频率；α=k3/m为陀螺驱动轴方向的非线性系数；kcv为陀螺仪表CV电路的 CV系数，表征单位振幅的检测输出电压变化量；Vout为陀螺驱动轴在不同激励下的谐振峰值。

由式(5)知，在非线性振动的条件下，系统的谐振频率是一个与振幅相关的抛物线。可以根据式(5)，进行曲线拟合，获得MEMS谐振器的固有频率f0和对应的非线性系数α，实现对MEMS谐振器非线性系数的表征。

2.2 实验数据处理

实验选取2只同批次的陀螺，对其驱动轴进行正弦扫频测试，扫描频率变化范围在陀螺的谐振区域。实验中，逐渐增大陀螺的驱动激励，在幅值未发生突变前，测得一系列不同激励下的的谐振峰值以及对应的谐振圆频率。表2为实验测得的部分数据，不难发现，陀螺的谐振频率随振幅的增大而增大。

表2 谐振峰值及其对应的频率值

为了从实验数据中拟合出陀螺驱动轴方向的振动非线性系数，结合式(5)，采用最小二乘法进行拟合处理，曲线拟合结果如图5所示。

图5 陀螺驱动轴幅频响应曲线

陀螺仪表的CV系数kcv=1.957×105V/m，驱动轴的等效质量m=1.127×10-7kg，结合式(3)和式(5)，得到的2只陀螺驱动轴的非线性系数α如表3所示。

表3 陀螺驱动轴方向非线性系数

2只陀螺的非线性系数α值与理论值相比，误差较小，充分证明了本文测量方法的正确性。

3 陀螺驱动轴的激励阈值

假设陀螺驱动轴非线性迟滞效应消失的临界点是其幅频曲线的多值现象的消失点，即响应幅值与频率是一一对应的关系，则该推导转变为使得右半段幅频曲线的斜率一直小于0的条件求解。基于达芬方程，陀螺驱动轴右半边幅频特性曲线的数学表达式为

(6)

式中ω0为固有圆频率；α为非线性系数；ζ为阻尼比；P为等效简谐力；ω为简谐力的频率；A为振幅。

若使得dω/dA≤0，有

(7)

因此，系统激励阈值P和系统振动阈值A分别为

(8)

(9)

陀螺驱动梳齿产生的驱动力可近似计算[13]，以陀螺1为例，实验中，陀螺驱动轴驱动梳齿的直流偏置电压为10 V，实验测得的自然频率为15.117 kHz，阻尼比ζ=1.602 5×10-5，要使得陀螺非线性迟滞效应消失，则要求交流激励幅值电压Vac≤ 0.056 9 V。

图6为激励交流幅值在0.05 V左右的扫频实验数据，当交流电压幅值为0.044 V时，陀螺驱动轴的振动特性虽然表现出比较明显的非线性振动特性，但其频率特性曲线依然连续，并未出现幅值突变现象，但当交流电压幅值等于0.056 V时，陀螺驱动轴的幅频和相频曲线均产生比较明显的突变。这与理论计算结果相吻合。

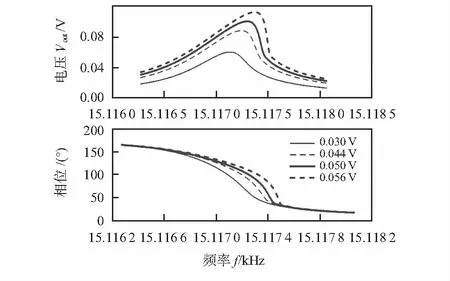
图6 陀螺驱动轴正弦扫频曲线

4 结 论

针对线振动MEMS陀螺驱动轴的振动非线性问题展开研究，重点讨论了谐振梁的非线性系数，基于达芬方程，利用其谐振频率曲线拟合得到陀螺驱动轴的非线性系数。结果表明：实验值和理论推导值相吻合。

从稳定性出发，推导计算得到陀螺的激励阈值和振幅阈值，为陀螺结构设计提供了参考。结果表明：非线性跳跃现象消失点的理论值与实验结果相吻合。陀螺驱动轴的非线性系数降低100倍，其振幅阈值增大10倍。

本文仅讨论了系统的结构非线性，并未涉及其他方面的非线性的讨论，有待进一步的研究。

[1] 李红光.现代军用MEMS惯性传感器技术进展[J].传感器与微系统,2014,33(8):4-7.

[2] 施常勇,张 肖.MEMS 陀螺在航天器控制系统中的应用评述[J].传感器与微系统,2015,34(7):1-5.

[3] 赵正平.典型MEMS和可穿戴传感技术的新发展[J].微纳电子技术,2015,52(1):1-13.

[4] Nitzan S.Impact of gyro.operation above the critical bifurcation threshold on scale factor and bias instability[C]∥Proc of MEMS 2014,San Francisco:749-752.

[5] 梁新建,郑旭东,李丹东，等.一种基于高线性度弓形支撑梁的新型MEMS陀螺设计[J].导航与控制,2011,10(3):49-53.

[6] Ehsan M M,Hossein N P,Aghil Y K,et al.Chaos prediction in MEMS-NEMS resonators[J].Internaional Journal of Engineering Science,2014,82:74-83.

[7] Siewe M,Usama H H.Homoclinic bifurcation and chaos control in MEMS resonators[J].Applied Mathematical Modelling,2011,35:5533-5552.

[8] 樊尚春，乔少杰，张 轩.谐振式硅微结构压力传感器非线性振动特性研究[J].仪器仪表学报,2006,27(12):1670-1673.

[9] Moorthi P,Lynn K.Nonlinear behavior of SOI free micromechanical beam resonator[J].Sensors and Actuators A,2008,142:203-210.

[10] 宋震煜,于 虹.纳米梁非线性振动的动力学分析[J].MEMS器件与技术,2006(3):145-149.

[11] Zhang W H,Baskaran Rajashree,Turner K L.Effect of cubic nonlinearity on auto-parametrically amplified resonant MEMS mass sensor[J].Sensors and Actuators,2002,102:139-150.

[12] Shao L C,Niu T,Palaniapan M.Nonlinearities in a high-Q SOI Lam’e-mode bulk resonator[J].J Micromech Microeng,2009,19:715-724.

[13] 郭秋芬.微型梳状线振动陀螺仪特性及干扰因素影响的研究[D].哈尔滨：哈尔滨工程大学，2007.