材料二次电子产额对腔体双边二次电子倍增的影响∗

董烨刘庆想 庞健周海京 董志伟

1)(西南交通大学物理科学与技术学院,成都 610031)

2)(北京应用物理与计算数学研究所,北京 100094)

3)(中国工程物理研究院流体物理研究所,绵阳 621900)

1 引 言

二次电子倍增是由二次电子驱动的一种真空共振放电现象,其可以在很多结构下产生,如:加速器、微波器件的腔体结构表面、微波输出窗表面以及人造卫星敏感器件内部,并导致严重后果,包括射频击穿、建场失败、沿面闪络以及噪声干扰等.作为一种最基本的二次电子倍增类型,金属双边二次电子倍增已经得到广泛研究.Vaughan[1]建立了细致的动力学理论分析模型并得到了聚焦相位条件;Kishek等[2]给出了共振方程并据此给出了双边二次电子倍增的敏感曲线;Kishek和Lau利用电子面片简化模型研究了双边二次电子倍增与外电路互作用的过程[3],最近Kishek还发现并证明了ping-pong类型双边二次电子倍增的存在[4].

国内外许多工作都是采用基于粒子轨迹跟踪的蒙特卡罗方法,对不同领域的二次电子倍增敏感区间进行预估和相关分析,由于蒙特卡罗方法并未考虑二次电子倍增过程中的空间电荷效应,因此无法获得完整的物理图像和深入认识[5−9].Gopinath等[10]首次使用粒子模拟(particle-in-cell)方法验证了Kishek动力学理论模型所得双平板二次电子倍增的相关规律.Riyopoulos[11]则单独讨论了空间电荷效应对双边二次电子倍增的影响.

针对加速器腔体射频建场过程[12−14]中二次电子倍增形成机理的研究需要,我们借鉴Kim和Verboncoeur[15]模拟介质窗二次电子倍增的思路,前期采用粒子模拟方法细致研究了金属双边二次电子倍增的瞬态及饱和特性,给出了二次电子倍增瞬态演化及饱和过程的物理图像[16].由于加速器腔体选用的是无氧铜材料,其材料二次电子产额系数较低(δmax0≈1.3,δmax0为材料正入射二次电子产额系数);而同样是基于双边二次电子倍增机理工作的微脉冲电子枪(如图1所示)通常选用的材料是金属表面氧化镁镀膜[17],其材料二次电子产额系数极高(δmax0≈16).Buyanova等[18]研究发现:平行平板结构中若二次电子产额超过某个阈值,可能会出现两个互不耦合的单边二次电子倍增取代双边二次电子倍增的现象,但其形成机理尚不明确.不同材料二次电子产额系数对腔体双边二次电子倍增的瞬态演化和饱和过程中所起的作用机理有何不同?本文在前期工作基础之上,重点研究了腔体内表面材料的不同二次电子产额对二次电子倍增形成及饱和阶段的影响过程.粒子模拟研究发现,二次电子倍增饱和阶段,高/低二次电子产额材料的饱和机制有所不同,导致其表现出的物理现象不同.

图1 微脉冲电子枪结构示意图Fig.1.Schematic of micro pulse electron gun.

2 物理建模

图2所示为腔体双边二次电子倍增简化模型,腔体间距为L,初始电子在射频电压VRF=VRF0sin(ωt+θ0)(VRF0为幅值,ω=2πf,f为工作频率,T为射频周期,f=1/T,θ0为初始相位)作用下,从腔体壁面一侧发射,经过半个射频周期(主模式)后获得能量轰击腔体另一侧壁面,激发出多于初始电子数目的二次电子,如此往复,便会出现二次电子倍增效应.当射频场频率、振幅以及器件结构参数达到某种匹配时,就有可能诱发双边二次电子倍增现象.本文采用粒子模拟与蒙特卡罗抽样算法(抽样二次电子的初始发射速度和角度)相结合的方法,从第一原理出发,研究与评估材料二次电子产额对腔体双边二次电子倍增瞬时特性的影响过程和作用机理.

图2 双边二次电子倍增示意图Fig.2.Schematic of two-sided multipactor discharge.

2.1 动力学方程与粒子模拟方法

模型中考虑了射频场与带电粒子产生的空间电荷场对粒子的双重作用,暂未考虑腔体加载效应的影响(即尚未考虑射频电压幅值VRF0与外电路联动的动态变化).

电子动力学方程如下:

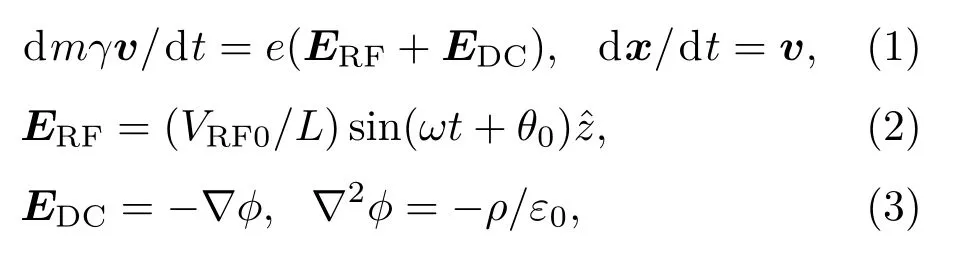
式中,ERF,EDC分别为射频电场强度矢量和电子产生的空间电荷场强度矢量;v,x,e,m和γ分别为电子速度矢量、位移矢量、电量、电子质量和相对论因子;ϕ,ρ分别为空间电荷静电势与电荷密度;ˆz为z方向单位矢量.EDC定义在网格中心;ϕ,ρ定义在网格结点位置.使用cloud-in-cell方法(线性插值的粒子模拟)将EDC权重到粒子位置,用同样方法将粒子电量权重到网格结点位置得出ρ.泊松方程可通过追赶法(一维情况)或松弛迭代求解(二维情况),ϕ求解后,通过中心差分求解可得EDC.我们编制了1D3V(一维三速)和2D3V(二维三速)粒子模拟(即1D3V-PIC和2D3V-PIC)程序.由于1D3V程序计算速度远快于2D3V程序,通过2D3V与1D3V程序模拟结果的比对,在完成1D3V程序正确性验证后,主要使用1D3V-PIC程序对不同材料二次电子产额情况下的腔体双边二次电子倍增瞬时演化及饱和特性相关物理规律进行研究.

2.2 材料二次电子发射模型

采用Vaughan[19]提出的二次电子产额经验拟合公式:

式中,

δ为二次电子产额系数;δmax0为正入射二次电子产额系数最大值;Emax0为δmax0对应的入射能量;δmax(α)为斜入射二次电子产额系数最大值;Emax(α)为δmax(α)对应的入射能量;α为入射角(α=0为正入射,α= π/2为掠入射);ks为表面光滑系数(ks=0,1,2,分别代表粗糙、不光滑和光滑);Ei为电子碰撞能量;Eth为能量阈值,一般取Eth=12.5 eV.δ＞1对应的碰撞能量分布范围(E1＜Ei＜E2,E1为二次电子倍增的碰撞能量下限值,E2为上限值)为材料二次电子倍增区间,其代表此区间内每个种子电子碰撞产生的二次电子数目大于1.

二次电子初始能量概率密度函数满足[20]:,其中,E0为二次电子出射能量;E0m是函数f(E0)峰值所对应的二次电子出射能量,E0m取值与材料特性有关,根据Vaughan的constant-k理论,一般取E0m=0.005Emax0.二次电子发射角ϕ是偏离平行出射表面方向的角度,其概率密度函数g(ϕ)满足[20]g(ϕ)=0.5sin(ϕ),ϕ取值范围0＜ ϕ ＜ π.本文采用蒙特卡罗方法对二次电子的出射能量和角度进行随机抽样.

3 数值模拟结果

粒子模拟中,设置射频频率f=72 MHz,板间距L=4cm,二次电子倍增发生面积A=1.77cm2,初始种子电子电流密度10µA/cm2(作用时间为射频注入开始后的一个周期内,位置随机出现在左右平板端面).由蒙特卡罗模拟得到射频电压幅值VRF0的二次电子倍增敏感区间(一阶)为420—810 V,不失一般性,设定射频电压幅值VRF0=550V,模拟中设置材料正入射二次电子产额最大值δmax0分别为1.3,2.0,3.0,12.0,16.0,研究不同材料的二次电子产额对金属双边二次电子倍增瞬时特性的影响规律和作用机理.

首先研究不同二次电子产额材料对二次电子倍增过程中宏观物理量瞬态演化特性的影响,包括二次电子数目、放电电流、放电功率和沉积功率等.某时刻电子数目通过对该时刻间隙空间内所有二次电子的数目累加求和获得.某时刻放电电流采用对该时刻所有二次电子的速度与电荷量乘积累加求和后,再除以间隙长度计算获得.放电功率通过瞬时射频电压与瞬时放电电流的乘积进行计算,沉积功率是时间步长内所有电子碰撞壁面损失能量除以时间步长后得到的数值.稳态阶段指的是二次电子倍增的趋于饱和后的阶段.

图3和图4分别给出了二次电子倍增瞬态演化过程中二次电子数量和放电电流随时间的演化关系,可以看出:二次电子数目和放电电流均随时间以指数形式快速增长后趋于饱和振荡.二次电子倍增发展阶段,二次电子数目增长率随材料二次电子产额增长呈现增加趋势;二次电子倍增饱和阶段,饱和二次电子数目及其振幅随材料二次电子产额增长亦呈现增加的规律.材料二次电子产额对放电电流的起振时间影响显著,随着材料二次电子产额的增长放电电流起振时间明显缩短.与稳态二次电子数目不同的是,稳态电流幅值随材料二次电子产额的增长呈现出非持续增长规律,而是逐渐增加后有所降低并趋于饱和的规律.

稳态放电功率波形如图5所示,稳态放电功率存在负值,说明二次电子倍增过程中存在充电现象,即电流波形相对电压存在延时效应.随着材料二次电子产额的增加,放电功率呈现正向幅值和负向幅值同时增加的规律(正向幅值绝对值大于负向幅值绝对值),而后稳态放电功率有所下降并最终达到惟一的饱和值.稳态沉积功率波形如图6所示,稳态沉积随时间演化呈现脉冲形式,这是由二次电子倍增相位聚焦区间决定的.随着材料二次电子产额的增加,沉积功率波形出现明显“拖尾”现象直到趋于饱和,该现象是材料二次电子产额增加导致二次电子数目增加,引发愈发强烈的空间电荷效应所导致的.

图3 二次电子数量随时间演化关系Fig.3.Electron number vs.time.

图4 放电电流随时间演化关系Fig.4.Discharge current vs.time.

图5 稳态放电功率Fig.5.Discharge power in saturation stage.

其次,通过分析讨论电子相空间、电荷密度、空间电荷场时空分布以及平均二次电子产额、平均碰撞能量、放电电流、间隙电压与二次电子数目的相互关系,细致研究了低二次电子产额(δmax0=1.3)和高二次电子产额(δmax0=16.0)材料对二次电子倍增不同的影响过程和作用机理.

图7和图8分别给出了稳态时二次电子相空间和电荷密度分布状态,可以看出:对于低二次电子产额材料,电荷密度最大值位于壁面位置附近,电子渡越过程中,电荷密度逐渐降低但空间分布逐渐变宽,这是由出射电子速度杂散效应以及空间电荷效应共同引发的,相空间上存在许多杂散的电子分布,说明稳态阶段的空间电荷效应较为强烈,电子间的排斥作用较为明显;对于高二次电子产额材料,大部分电子集中分布在腔体壁面附近,间隙内的电子渡越运动受到了明显的抑制,间隙内未形成明显的“空间群聚”现象,电荷密度最大值出现在金属壁面附近并明显高于低二次电子产额材料情况下的电荷密度最大值,间隙内部存在数值极低的电荷密度分布,表明空间电荷效应随着材料二次电子产额的增加呈现出明显增强的趋势.

图6 稳态沉积功率Fig.6.Deposited power in saturation stage.

图7 稳态电子相空间分布(a)δmax0=1.3;(b)δmax0=16Fig.7.Electron phase-space distribution in saturation stage:(a) δmax0=1.3;(b) δmax0=16.

图8 稳态电荷密度空间分布(a)δmax0=1.3;(b)δmax0=16Fig.8.Charge density distribution in saturation stage:(a) δmax0=1.3;(b) δmax0=16.

图9给出了稳态电子数目、二次电子产额、碰撞能量关系,可以看出:低二次电子产额情况下,二次电子数目、平均二次电子产额和碰撞能量的脉宽较宽,二次电子数目下降段对应平均碰撞能量和二次电子产额的下降段(空间电荷“反场”效应)和剧烈振荡段(空间电荷“去群聚”效应);高二次电子产额情况下,二次电子数目、平均二次电子产额和碰撞能量的脉宽较窄,二次电子数目下降段主要对应平均碰撞能量和二次电子产额的下降段(空间电荷“反场”效应),平均碰撞能量和二次电子产额小幅振荡段对应的二次电子数目下降速度较缓.

图10给出了稳态电子数目、间隙电压、放电电流关系,可以看出:二次电子倍增过程中,放电电流波形较间隙射频电压波形存在明显的延时效应.对于低二次电子产额材料,二次电子数目脉宽较宽,振荡幅度较小,放电电流波形类似“三角波”分布;对于高二次电子产额材料,二次电子数目脉宽较窄,振荡幅度较大,放电电流波形类似“正弦波”分布.

上述现象表明:虽然在二次电子倍增发展阶段,双边二次电子倍增的特性与材料二次电子产额无关(此阶段空间电荷效应可以忽略);但是,当二次电子倍增进入饱和阶段,随着材料二次电子产额的增加,腔体双边二次电子倍增将会向单边二次电子倍增类型转变.较高的二次电子产额材料,在二次电子倍增达到饱和时,更倾向趋于单边二次电子倍增类型分布(图8(b)所示).

图9 稳态电子数目、二次电子产额及碰撞能量关系(a)δmax0=1.3;(b)δmax0=16Fig.9.The evolution relationship of the electron number,secondary electron yield(SEY)coeffcient and impact energy in saturation stage:(a) δmax0=1.3;(b) δmax0=16.

图10 稳态电子数目、间隙电压及放电电流关系(a)δmax0=1.3;(b)δmax0=16Fig.10.The evolution relationship of electron number,gap voltage and discharge current in saturation stage:(a) δmax0=1.3;(b) δmax0=16.

4 结 论

本文采用蒙特卡罗抽样与粒子模拟相结合的方法,数值研究了材料二次电子产额对腔体双边二次电子倍增瞬态演化及饱和特性的影响.研究发现,随着材料二次电子产额的增加,二次电子增长率以及稳态二次电子数目和振幅均呈现增加的趋势,放电电流起振时间逐步缩短,稳态电流幅值以及放电功率的平均值和振幅值均呈现逐步增加并趋于饱和的规律,沉积功率波形延时以及脉宽呈现逐步增加并趋于饱和的趋势.

粒子模拟细致地给出了高/低二次电子产额情况下的电子相空间分布、电荷密度分布、平均碰撞能量、平均二次电子产额、二次电子数目和放电电流的物理图像.模拟结果表明:二次电子倍增饱和阶段,高/低二次电子产额材料的物理图像有所不同,低二次电子倍增产额材料下,间隙内电子的单向渡越“群聚”特性明显;高二次电子倍增产额材料下,电子基本位于壁面附近,渡越运动受到了明显的抑制.对于低二次电子产额材料,二次电子数目脉宽较宽,振荡幅度较小,放电电流波形类似“三角波”分布;对于高二次电子产额材料,二次电子数目脉宽较窄,振荡幅度较大,放电电流波形类似“正弦波”分布.电荷密度最大值均出现在金属壁面附近,且高二次电子产额材料的电荷密度明显高于低二次电子产额材料情况.

随着材料二次电子产额的增加,双边二次电子倍增将会向单边二次电子倍增类型转变.较高的二次电子产额材料,在二次电子倍增达到饱和时更倾向趋于单边二次电子倍增类型分布.究其作用机理,二次电子倍增过程中空间电荷场起到了两方面作用:其一,导致电子碰撞相位发散,使电子溢出聚焦相位区间;其二,导致发射面电场呈现“反场”效应阻止二次电子的发射.低二次电子产额材料情况下,二次电子倍增的饱和特性是由空间电荷场的“去群聚”效应和“反场”效应同时决定的;而高二次电子产额材料情况下,二次电子倍增的饱和特性主要是由发射面空间电荷场的“反场”效应决定的.

[1]Vaughan J R M 1988 IEEE Trans.Electron Dev.35 1172

[2]Kishek R A,Lau Y Y,Ang L K,Valfells A,Gilgenbach R M 1998 Phys.Plasmas 5 2120

[3]Kishek R A,Lau Y Y 1995 Phys.Rev.Lett.75 1218

[4]Kishek R A 2012 Phys.Rev.Lett.108 035003

[5]Zhang P,Lau Y Y,Franzi M,Gilgenbach R M 2011 Phys.Plasmas 18 053508

[6]Sazontov A G,Nechaev V E,Vdovicheva N K 2011 Appl.Phys.Lett.98 161503

[7]Sazontov A,Buyanova M,Semenov V,Rakova E,Vdovicheva N,Anderson D,Lisak M,Puech J,Lapierre L 2005 Phys.Plasmas 12 053102

[8]Zhang X,Wang Y,Fan J J 2015 Phys.Plasmas 22 022110

[9]Li Y D,Yan Y J,Lin S,Wang H G,Liu C L 2014 Acta Phys.Sin.63 047902(in Chinese)[李永东,闫杨娇,林舒,王洪广,刘纯亮2014物理学报63 047902]

[10]Gopinath V P,Verboncoeur J P,Birdsall C K 1998 Phys.Plasmas 5 1535

[11]Riyopoulos S 1997 Phys.Plasmas 4 1448

[12]Devanz G 2001 Phys.Rev.Special Topics-Accelerators and Beams 4 012001

[13]Xu B,Li Z Q,Sha P,Wang G W,Pan W M,He Y 2012 High Power Laser and Particle Beams 24 2723(in Chinese)[徐波,李中泉,沙鹏,王光伟,潘卫民,何源 2012强激光与粒子束24 2723]

[14]Wang C,Adelmann A,Zhang T J,Jiang X D 2012 High Power Laser and Particle Beams 24 1244(in Chinese)[王川,Andreas Adelmann,张天爵,姜兴东2012强激光与粒子束24 1244]

[15]Kim H C,Verboncoeur J P 2005 Phys.Plasmas 12 123504

[16]Dong Y,Liu Q X,Pang J,Yang W Y,Zhou H J,Dong Z W 2017 Acta Phys.Sin.66 207901(in Chinese)[董烨,刘庆想,庞健,杨温渊,周海京,董志伟 2017物理学报66 207901]

[17]Liao L,Zhang M,Gu Q 2013 Nucl.Instrum.Meth.Phys.Res.A 729 381

[18]Buyanova M,Semenov V E,Anderson D,Lisak M,Puech J 2010 Phys.Plasmas 17 043504

[19]Vaughan J R M 1993 IEEE Trans.Electron Dev.40 830

[20]Kishek R A,Lau Y Y 1998 Phys.Rev.Lett.80 193