耦合双泡声空化特性的理论研究∗
王德鑫 那仁满都拉
(内蒙古民族大学物理与电子信息学院,通辽 028043)
1 引 言
液体中的微小气泡在超声作用下会发生一系列的非线性振荡,这就是声空化.空化气泡内部的极端条件可能会促进液体中的物理化学反应,并在一定条件下会伴随光辐射现象,这就是声致发光.最早对于液体中空化气泡的理论研究是Rayleigh建立的球形空腔的气泡动力学理论模型[1].之后人们不断对其进行改进和完善,提出了经典的Rayleigh-Plesset方程[2]和常用的Keller-Miksis(K-M)方程[3].这些模型对于研究声致发光现象的内在机理有重要意义.
有研究表明,在多泡声致发光(MBSL)中,气泡半径的大小随着超声波频率的减小而增加[4].Ida等[5]对不同多泡模型进行了研究,并且对液态汞中空化气泡进行了观察.王成会等[6]从气泡辐射场影响下的均匀球状气泡群的耦合振动以及非线性声响应方面分析了增强和抑制泡群空化的因素.由于空化和MBSL的复杂性,为简化模型以便于贴近实际环境,人们开始关注双泡的理论研究.Mettin等[7]通过考虑气泡的非线性振动,研究了水中不同驱动压力下的双泡之间的相互作用力.卢义刚和吴雄慧[8]由速度势叠加原理得到双泡超声空化方程并对其运动规律进行了分析.蒲中奇等[9]建立了空化泡辐射噪声的理论模型,对双泡在崩溃时空化噪声规律进行了分析.在双泡的实验研究中,Shirota等[10]利用声致发光的实验系统观察了双泡的运动轨道,同年张文娟和安宇[11]对实验中观察到的双泡相互绕圈运动的现象进行了理论研究.Rasoul等[12]分析了不同浓度硫酸溶液中两个声致发光气泡间的次Bjerknes力.
Bjerknes力是声场对气泡的作用力,具体可表现为:单个气泡在静止声场的压力节点或波腹处的吸引或排斥现象,以及振荡气泡的相互吸引或排斥现象.当影响气泡的力是由外加声场作用引起的时,其被称为“主Bjerknes力”;由于相邻气泡辐射声场引起的两个气泡之间的力称为“次Bjerknes力”[7].关于气泡间的次Bjerknes力,早在1993年Pelekasis和Tsamopoulos[13,14]采用混合边界的有限元法,通过对无限远流体静压力的阶跃性变化和振荡压力场下双泡间的次Bjerknes力的研究来说明它们的形变和界面的电位变化.通过将平均Bjerknes力与平均浮力相等的方法,计算了稳定声波中的单泡声致发光气泡的平衡位置[15].由于次Bjerknes力对气泡体积的影响,马艳等[16]利用Lagrange方程推导出了次Bjerknes力作用下气泡体积的振动方程,并探讨了次Bjerknes力作用下不同参数对气泡体积振动振幅和振动初相位的影响.胡静等[17]在考虑了不同泡群间的次级辐射声响因素,对不同大小泡群间的相互作用进行了分析.为了更贴近实际情况,在空化气泡非球形效应的基础上,马艳等[18]对非球形空化气泡和球形气泡间的次Bjerknes力的影响因素进行了分析讨论.
本文通过考虑双泡之间的辐射压力波,利用改进的K-M方程和van der Waals方程,研究了不同大小、不同间距、含不同惰性气体的双泡在声空化过程中半径的变化、次Bjerknes力的变化和双泡内温度的变化.
2 耦合双泡动力学模型
当双泡中心间距足够小时,由于气泡间辐射压力波的存在,作用在气泡上的压力不等于外部驱动压力,所以必须考虑双泡之间的相互作用.假设双泡在振荡过程中位置保持不变,并且始终保持球形,双泡可以在驱动声场的作用下同步振荡.双泡中任一球形气泡的辐射压力可以从如下欧拉方程和流体介质的连续性方程获得[5]:
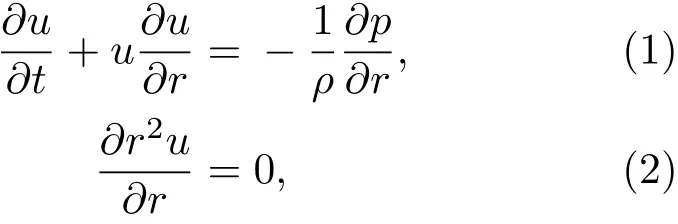
式中,u(r,t)和p(r,t)分别是气泡在液体中的速度和压力,r是气泡的径向坐标.气泡周围的速度场可以表示为
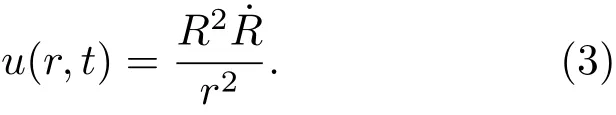
由(3)式可知u(R,t)=R˙(t),并假设u(r→∞,t)=0,则将(3)式代入(1)式并进行积分得
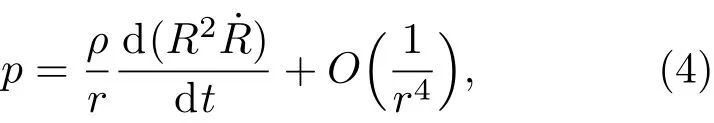
由于p(r→ ∞,t)=0,故可忽略无穷小项.在气泡1的压力梯度场∇P1的作用下,体积为V2的气泡2受到气泡1作用的次Bjernes力可表示为
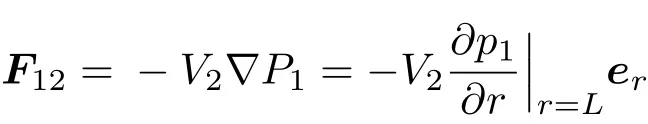
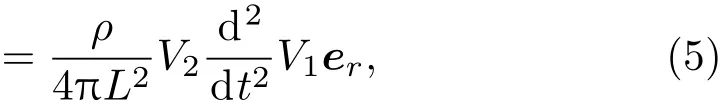
式中L,er分别为两个气泡之间的距离和径向单位矢量.(5)式两边对时间进行二次积分就可得到[12]
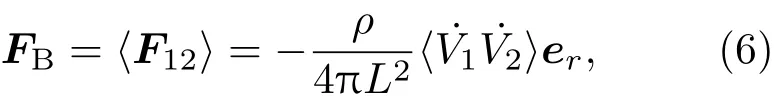
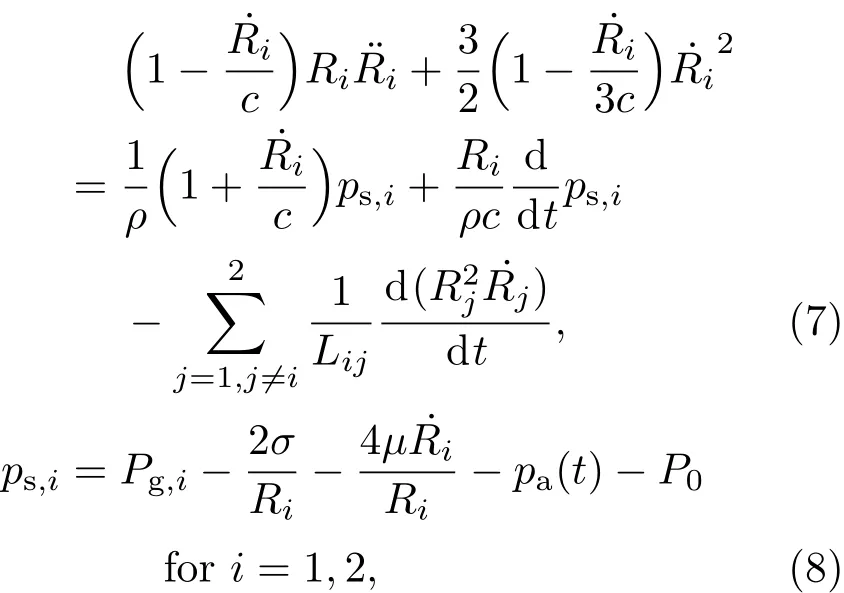
式中Lij是气泡i和气泡j的中心距离;pa(t)=−Pasin(ωt)为外部驱动力.(7)式中的最后一项是双泡之间的声场相互耦合作用项.假设气泡内部的气体为理想气体,因此气泡内气体压强的变化满足van der Waals方程:

式中,P0为环境压强,σ为液体的表面张力,Ri0是第i个气泡的初始半径,hi是第i个气泡的van der Waals硬核半径,γ为气体的多方指数.对于不同气体,多方指数γ可以通过下式得出[19]:
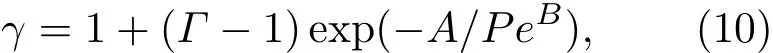
上式中瞬时Pelect数由式Pe=|R˙|R/κgas确定,其中κgas可由下式计算[19]:
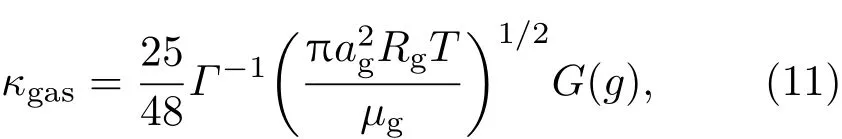
这里ag,Rg,T和µg分别是气体有效原子直径、理想气体常数、气体温度和气体分子质量,G(g)是一个无量纲的密度函数.考虑到气泡壁上气体热扩散所导致的气泡内部的温度变化,气泡内部温度的表达式修正为[19]
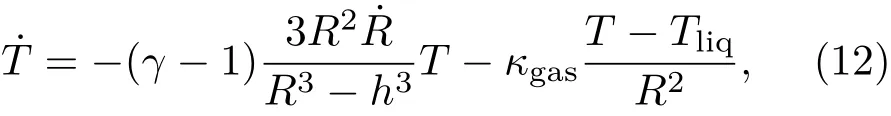
其中Tliq是无穷远处的液体温度.方程(12)与方程(7)给出了双泡系统中气泡半径和气泡内温度的计算模型.本文所采用的计算气泡内部温度的模型进行了较多的简化,并没有考虑气泡内的蒸汽压强,以及在气泡振荡过程中的热传导和质量交换.在下面的计算中各物理参数的初始值分别取为:µ =10−3Pa·s,c=1485 m/s,σ =0.0725 N·m−1,ρ=1000 kg/m3,f=20 kHz,Pa=1.3 atm,T0=293.13 K.
3 不同大小双泡的声空化特性
在MBSL实验中,所形成气泡的大小是随机的,因此研究不同大小双泡的相互作用对声空化特性的影响,在实验方面可以提供理论指导.本节考虑三种情况:1)双泡的大小分别为R10=2µm,R20=5µm;2)双泡的大小均为R10=R20=2µm;3)双泡的大小均为R10=R20=5µm.假设双泡处于耦合状态,即L=100µm,气泡内是Ar气,其van der Waals硬核半径为hAr=Ri0/8.86.另外在运动过程中双泡受到的次Bjerknes力是对称的,即〈Fij〉= −〈Fji〉[9],并且在本文的计算中忽略了延迟效应对次Bjerknes力的影响.利用改进的K-M模型,计算了不同大小耦合双泡的声空化特性,结果如图1所示.
图1显示的是耦合双泡大小对声空化气泡半径、次Bjerknes力和内部温度变化的影响.当双泡分别为2和5µm时,小气泡膨胀的最大半径为R1max=18.087µm,崩溃时间为22.6355µs,最高温度为3.8294×103K,大气泡膨胀的最大半径为R2max=50.919µm,崩溃时间为27.2705µs,最高温度为1.8729×104K,此时最大正次Bjerknes力为2.8426 × 10−6N,最大负次Bjerknes力为2.5546×10−6N;当双泡大小均为2µm时,双泡振荡的频率是一样的,膨胀的最大半径为Rmax=28.647µm,崩溃时间为24.632µs,最高温度为1.1958×104K,此时最大次Bjerknes力为1.6899×10−5N;当双泡大小均为5µm时,膨胀的最大半径为Rmax=46.368µm,崩溃时间为27.664µs,最高温度为1.6608×104K,此时最大次Bjerknes力为1.5976×10−4N.
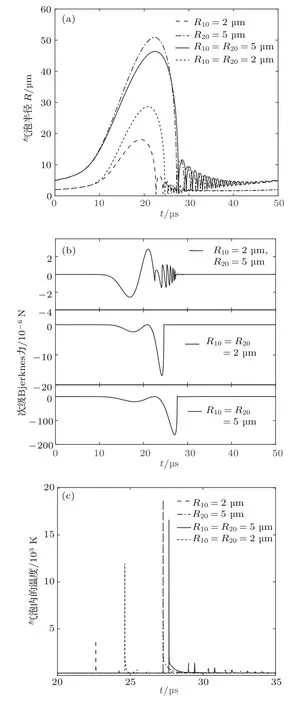
图1 一个周期内不同大小双泡的声空化特性的变化(a)气泡半径;(b)次Bjerknes力;(c)气泡内温度Fig.1.Property changes of ultrasonic cavitation of the double bubbles with different sizes in one period:(a)Radius of bubble;(b)secondary Bjerknes force;(c)temperature of bubble.
从图1(a)和图1(b)以及上面的数据可以看出,当两个气泡大小不同时,次Bjerknes力主要的贡献来自于大气泡在第一次溃灭之前气泡壁运动.当小气泡溃灭之后,因为辐射压力场的耦合将次Bjerknes力由吸引力转变为排斥力,这就意味着在两个气泡之间存在着一个平衡点[7].在大气泡溃灭后的反弹阶段由于快速的振荡,平均的次Bjerknes力约为零.当两个气泡大小相同时,从图1(b)可以看出在一个周期内次Bjerknes力属于吸引力,并且在一个周期内次Bjerknes力有两次径向振荡,第一次在20µs左右,第二次在气泡发光的瞬间,说明在膨胀和崩溃过程中双泡是相互吸引的[11].

图2 一个周期内耦合双泡和单泡的气泡半径和气泡内温度的变化(R1,R2为单泡模型气泡初始半径;R10,R20为双泡模型的两个气泡初始半径)Fig.2.Changes of radius and temperature of the coupling double bubbles and the single bubble in one period(R1and R2are the initial radii of bubbles in the single bubble model,R10and R20are the initial radii of bubbles in the double bubbles model,respectively).
从图1(c)可以看出,当双泡大小不同时,双泡间的相互作用对小气泡的影响比大气泡大,在小气泡崩溃过程中大气泡会对小气泡起到非常明显的抑制作用,使其内部温度与相同半径双泡相比明显降低.对于大气泡,相互作用力与半径相同时的大气泡相比降低,使得大气泡在溃灭时温度有所提高.为了研究双泡大小不一样时哪个气泡受影响的程度比较大,研究了初始半径为2和5µm的耦合双泡的半径变化和内部温度变化,并与初始半径为2和5µm的单泡的半径变化和温度变化进行了比较,结果如图2所示.当单泡半径R1=2µm时,膨胀的最大半径Rmax=30.670µm,崩溃时间为24.490µs,最高温度为1.2609×104K;当单泡半径为R2=5µm时,膨胀的最大半径Rmax=50.819µm,崩溃时间为27.2485µs,最高温度为1.8456×104K.
可以看出,双泡中半径2µm的气泡比初始半径为2µm的单泡膨胀的最大半径减少将近12µm,由于膨胀半径的减小,直接导致气泡内部的温度下降了约104K.初始半径为5µm的单泡与双泡中5µm的气泡半径相比几乎没有变化,气泡内部的温度同样没有明显的变化.由此可以看出,大气泡辐射出的声压相对于小气泡来说非常大,对小气泡的运动起到了非常明显的抑制作用,而小气泡对大气泡的影响却很微弱.因此,当双泡大小不同时,大气泡对小气泡有非常明显的抑制作用.该结论与文献[19]中两个半径大小不一样的球形气泡群相互作用时的结论类似.
4 不同间距双泡的声空化特性
对于双泡声空化问题中,双泡之间的距离是影响双泡空化特性的一项非常重要的因素.通过文献[9]可知,如果双泡间距非常小,它们之间的相互运动就受到影响.本节考虑水中不同间距的两个大小相同的气泡,并假设双泡的大小均为4.5µm,气泡内部气体都为Ar气.下面分别计算双泡间距L=100µm,1 mm,1cm时气泡半径、次Bjerknes力以及气泡内部温度的变化情况.
计算结果表明:当L=100µm时,气泡的崩溃时间为27.372µs,膨胀的最大半径为44.550µm,最大次Bjerknes力为1.3286×10−4N,最高温度为1.6932×104K;当L=1 mm时,气泡的崩溃时间为27.0395µs,膨胀的最大半径为48.205µm,最大次Bjerknes力为2.1165×10−6N,最高温度为1.7608×104K;当L=1cm时,气泡的崩溃时间为26.994µs,膨胀的最大半径为48.867µm,最大次Bjerknes力为2.2390×10−8N,最高温度为1.8814×104K.
从图3(a)可以清晰地看到随着双泡间距的增加,双泡膨胀的最大半径也在逐渐增大,从崩溃放大图可看出气泡的崩溃时间明显提前,这与文献[8]中的计算结果是一致的.随着双泡间距的增大,气泡壁膨胀的曲线趋于重合,说明当双泡间距大于一定值时,可以将其简化成单泡模型.
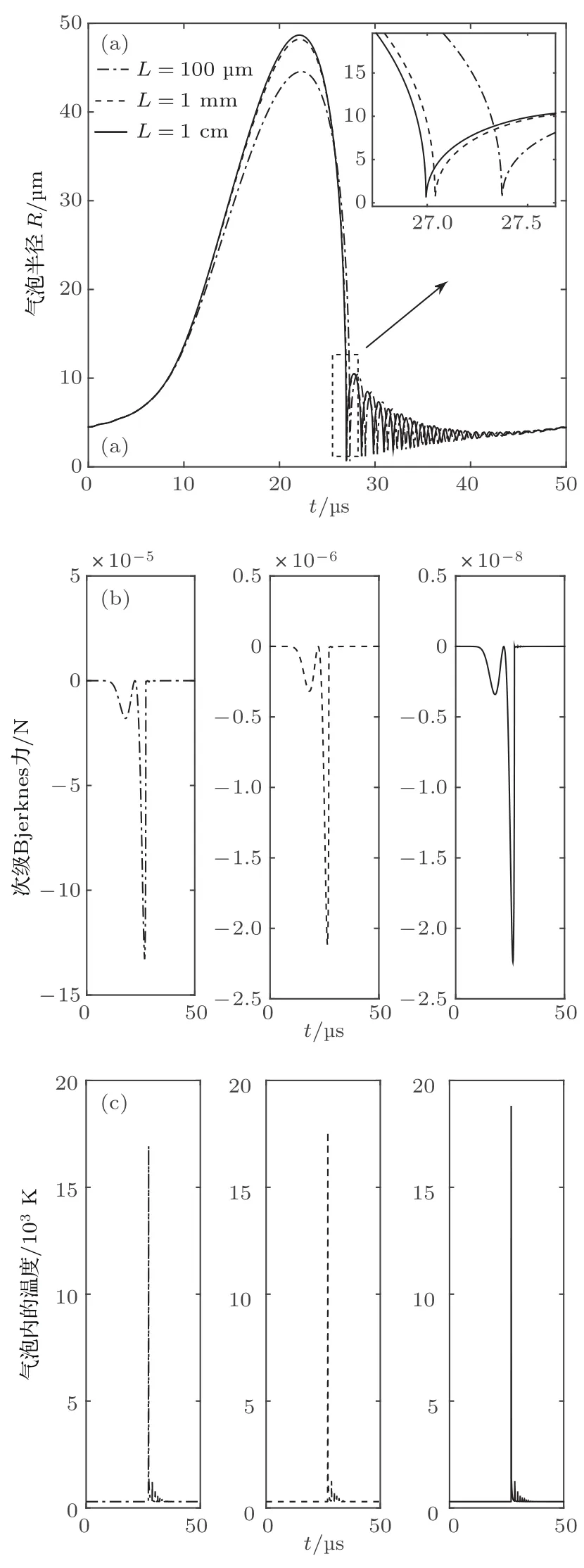
图3 一个周期内不同间距双泡的声空化特性的变化(a)气泡半径;(b)次Bjerknes力;(c)气泡内温度Fig.3.Property changes of ultrasonic cavitation of the double bubbles with different distances in one period:(a)Radius of bubble;(b)secondary Bjerknes force;(c)temperature of bubble.
图3(b)表示的是不同间距下计算出的双泡间次Bjerknes力,三种情况对比可以看出,随着双泡间距的增加,次Bjerknes力的数量级从10−4N减小到10−8N,即气泡间相互作用力的大小随着气泡间距的减小而增大.文献[12]中认为当双泡间距为1cm时处于未耦合状态,从计算结果可以看出此时气泡间次Bjerknes力的数量级为10−8N,基本可以忽略不计.这说明双泡间的次Bjerknes力随着双泡间距的增大而逐渐衰减,当双泡间距大于1cm时逐渐衰减为零[18].从图3(c)气泡内部温度的变化可以看出,随着双泡间距的增加,双泡间相互作用力的减小,它们内部的温度也在增加.
5 含不同惰性气体双泡的声空化特性
惰性气体在声致发光过程中的作用是非常明显的,有研究表明当空气泡中注入1%的Ar气时,在声致发光过程中所发出的光与未注入Ar气相比亮度增加几百倍[20],且惰性气体对声致发光光谱的研究也有重要作用[21].因此在双泡声空化中不同惰性气体的影响也是必须考虑的一个因素.通过文献[22]可知,在声致发光过程中随着气泡中惰性气体分子量的增加,气泡的相对半径变化不明显,但是所产生的温度和亮度都随之增加.
本节考虑双泡由不同惰性气体构成,双泡大小均为4.5µm,双泡间距L=100µm,计算中采用的惰性气体参数列于表1.

表1 不同惰性气体的参数[19]Table 1.The characteristic parameters of the noble gases[19].
图4为含不同惰性气体双泡在声空化过程中其半径和温度的变化.计算结果表明,当泡1内含有Xe气、泡2内含有Ar气时,双泡膨胀的最大半径分别为44.554,44.549µm,最高温度分别为3.3766×104,1.6869×104K,崩溃时间分别为27.3725,27.3721µs,最大次Bjerknes力为1.3288×10−4N;当泡1内含有Xe气、泡2内含有He气时,两气泡膨胀的最大半径分别为44.559,44.532µm,最高温度分别为3.3676×104,7.0395×103K,崩溃时间分别为27.3725,27.3705µs,最大次Bjerknes力为1.3280×10−4N.
两种情况的比较可看出,不同的惰性气体对耦合双泡膨胀的最大半径的影响很小.但从放大图4(b)和图4(e)可以看出,不同的惰性气体气泡在回弹阶段表现出明显不同的振荡规律,即半径的变化明显不同.这由于在气泡膨胀和收缩的过程可以看作是等温过程,此时气体的多方指数γ≈1,所以不同惰性气体对气泡膨胀和收缩过程中半径的影响可以忽略.在气泡崩溃的瞬间,气泡内部可以看作是绝热过程,由(10)式可知分子量大的惰性气体的多方指数的变化快,影响了气泡内部气体压强,导致在第二个膨胀过程中膨胀的最大半径的差异,进而影响了回弹阶段的振荡.
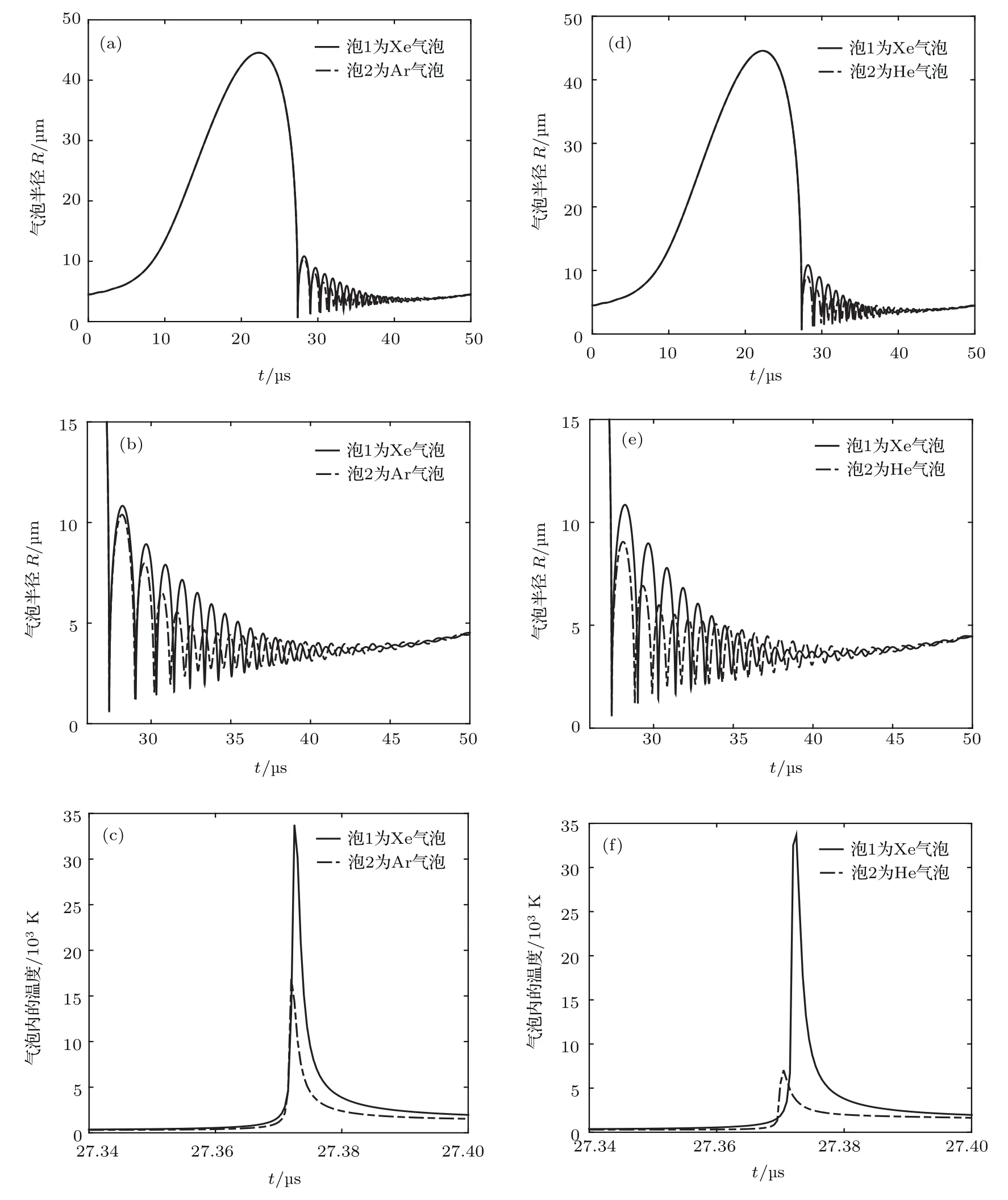
图4 一个周期内不同惰性气体双泡的声空化特性的变化(a)Xe气泡和Ar气泡的半径;(b)图(a)回弹阶段的放大图;(c)Xe气泡和Ar气泡内温度;(d)Xe气泡和He气泡的半径;(e)图(d)回弹阶段的放大图;(f)Xe气泡和He气泡双泡内温度Fig.4.Property changes of ultrasonic cavitation of the double bubbles with different noble gas in one period:(a)Radius of Xe and Ar bubble;(b)magni fied figure of panel(a)in the stage of rebound;(c)temperature of Xe and Ar bubble;(d)radius of Xe and He bubble;(e)magni fied figure of panel(d)in the stage of rebound;(f)temperature of Xe and He bubble.
由(6)式可知,最大次Bjerknes力与气泡膨胀最大半径的平方成正比,因此不同惰性气体对双泡间的相互作用力大小的影响是不明显的,所以没有给出次Bjerknes力的变化图.由于单泡和双泡内温度的计算都与气泡内部气体和气泡膨胀的半径有关,当双泡含有相同的惰性气体且膨胀的最大半径相同时,单泡和双泡声空化时内部温度是一样的[19].当双泡分别含有不同的惰性气体且膨胀的最大半径也相同时,单泡和双泡都是分子量大的惰性气体气泡内部的温度更高,这表明耦合双泡声空化中惰性气体的作用与单泡声空化中的作用是一样的.
6 结 论
如果两个空化气泡间距足够小时,由于相邻气泡间的辐射压力波的存在,必须考虑它们之间的次Bjerknes力.本文通过考虑双泡间的相互作用,得到了次Bjerknes力的表达式,并通过双泡动力学方程对耦合双泡声空化时的气泡半径变化、气泡内温度变化以及次Bjerknes力变化进行了分析.
对于不同大小的双泡,由于大气泡的辐射压力波较强,所以小气泡受到抑制作用较强,温度变化也比较明显.当双泡大小相同时,双泡间的次Bjerknes力均为负,表明耦合的双泡在振荡过程中相互吸引,并且在一个周期内次Bjerknes力有两次径向振荡.随着双泡间距的增加,双泡间的相互影响减弱,因此双泡受到的次Bjerknes力逐渐减小,膨胀的最大半径在逐渐增大,并且气泡内温度也随之增加.当双泡间距足够大时,次Bjerknes力就可以忽略不计,可将双泡模型简化为单泡模型.
当双泡内含有不同惰性气体时,由于溃灭时气泡内气体的多方指数变化的差异导致在溃灭之后的回弹阶段表现出明显不同的振荡规律.而在双泡膨胀阶段多方指数不变,所以最大半径没有明显差异.本文的研究对于不同数量气泡的声空化模型的建立,以及不同数量气泡间相互作用的研究提供了理论基础.
[1]Rayleigh L 1917 Philos.Mag.34 94
[2]Plesset M S 1949 J.Appl.Mech.16 277
[3]Keller J B,Miksis M 1980 J.Acoust.Soc.Am.68 628
[4]Kyuichi Y 2002 J.Acoust.Soc.Am.112 1405
[5]Ida M,Naoe T,Futakawa M 2007 Phys.Rev.E 76 046309
[6]Wang C H,Mo R Y,Hu J,Chen S 2015 Acta Phys.Sin.64 234301(in Chinese)[王成会,莫润阳,胡静,陈时2015物理学报64 234301]
[7]Mettin R,Akhatov I,Parlitz U,Ohl C D,Lauterborn W 1997 Phys.Rev.E 56 2924
[8]Lu Y G,Wu X H 2011 Acta Phys.Sin.60 046202(in Chinese)[卢义刚,吴雄慧 2011物理学报 60 046202]
[9]Pu Z Q,Zhang W,Shi K R,Zhang J H,Wu Y L 2005 J.Tsinghua Univ.(Science and Technology)45 1450(in Chinese)[蒲中奇,张伟,施克仁,张俊华,吴玉林 2005 清华大学学报:自然科学版45 1450]
[10]Shirota M,Yamashita K,Inamura T 2012 AIP Conf.Proc.1474 155
[11]Zhang W J,An Y 2013 Tech.Acoust.32 125(in Chinese)[张文娟,安宇 2013声学技术 32 125]
[12]Rasoul A,Rezaee N,Ebrahimi H,Mirheydari M 2010 Phys.Rev.E 82 016316
[13]Pelekasis N A,Tsanopoulos J A 1993 J.Fluid Mech.254 467
[14]Pelekasis N A,Tsanopoulos J A 1993 J.Fluid Mech.254 501
[15]Matula T J,Cordry S M,Roy R A 1997 J.Acoust.Soc.Am.102 1522
[16]Ma Y,Lin S Y,Xian X J 2016 Acta Phys.Sin.65 014301(in Chinese)[马艳,林书玉,鲜晓军 2016物理学报 65 014301]
[17]Hu J,Lin S Y,Wang C H,Li J 2013 Acta Phys.Sin.62 134303(in Chinese)[胡静,林书玉,王成会,李锦 2013物理学报62 134303]
[18]Ma Y,Lin S Y,Xu J,Tang Y F 2017 Acta Phys.Sin.66 014302(in Chinese)[马艳,林书玉,徐洁,唐一璠2017物理学报66 014302]
[19]Hilgenfeldt S,Grossmann S,Lohse D 1999 Phys.Fluids 11 1318
[20]Hiller R,Putterman S J,Barber B P 1992 Phys.Rev.Lett.69 1182
[21]Zhou C,Chen W Z,Cui W C 2013 Acta Phys.Sin.62 087805(in Chinese)[周超,陈伟中,崔炜程2013物理学报62 087805]
[22]Gheshlaghi M 2015 Ext.J.Appl.Sci.3 257

