二维情况下两组分带电囊泡形变耦合相分离的理论模拟研究∗

段华 李剑锋 张红东

(复旦大学高分子科学系,聚合物分子工程国家重点实验室,上海 200433)

1 引 言

两亲性脂质分子、表面活性剂以及嵌段共聚物等在溶液中易自发组装成各种形态,例如:片状膜、胶束、囊泡等.囊泡乃两亲性双分子层通过卷曲形成的一种内部包含溶剂分子的封闭膜泡.虽然囊泡结构极其简单,但由于其物理上与生物体系中细胞结构存在共性,故可结合经典弹性膜理论[1]、用囊泡物理模型解释一些生命现象,例如红细胞的双凹碟状[1],红细胞的SDE序列转变[2,3]等.然而,真实的生物膜十分复杂,为多组分且通常带一定电荷,故研究带电多组分囊泡具有重要的生物学意义.此外,多年来人们感到不解,生物膜一般为多组分,通常多组分聚集体都容易出现同种组分团聚现象,过分的团聚行为必定影响其生理功能的实现,那么生命体是如何克服这种团聚现象的呢?人们猜测静电相互作用或许可帮助增加不同生物分子间的相溶性,而具体机理人们并不非常清楚.因此有必要对带电多组分囊泡的相分离现象进行细致的理论模拟研究[4−11].

然而,目前的研究要么只针对多组分囊泡,要么只针对带电囊泡,极少将两者结合起来.

其中多组分囊泡相关的研究已经比较多.例如,Jørgensen等[12,13]通过将实验数据与蒙特卡罗模拟相结合的方法研究了两组分的非平衡有序化过程对局部和整体侧向膜结构的影响,提出非平衡态效应会影响微相区的形成;Suni-Kumar等[14]采用动态三角网格划分的蒙特卡罗方法研究了两组分囊泡相分离的形变动力学,他将出芽的过程分为膜内区域的形成和生长、形成许多小芽、小芽融合再长大三个阶段,并给出了后期凸芽生长动力学随时间的标度关系;之前,我们采用球冠模型与耗散动力学方法系统研究了两组分囊泡的相分离和出芽的过程,发现组分的自发曲率及相区界的界面能会影响出芽的数目以及出芽的方式,增加其中一个组分的自发曲率会增加出芽的数目,并给出了一个相对完整的相图[5];此外,耗散粒子动力学模型[15,16]以及时间依赖的Ginzburg-Landau(TDGL)[17]动力学等方法也被用于研究多组分囊泡中的相分离微相区的生长.

单组分带电囊泡的模拟研究则较少报道,主要存在数值计算困难,难以模拟大变形及静电作用较强时的情形,导致大多研究不成系统性.Sinha和Thaokar[18]认为我们之前的工作[19]是目前仅有关于单组分带电囊泡的系统研究工作,在这篇报道中我们给出了不同带电量不同约化体积条件下的三维带电囊泡平衡态形状.

关于带电多组分囊泡的系统性研究则更少,目前只有分子动力学相关的粒子模拟[20].主要是因为首先带电囊泡的影响因素较多,很难进行系统性研究,其次理论和模拟中处理多组分和处理静电相互作用都存在一定的困难,现在两个困难叠加,使得模拟计算极不稳定.本文希望离散空间变分法[21]与耗散动力学方法[17]结合可用于克服这些困难,为简单起见,只考察二维两组分带电囊泡的形变耦合相分离行为,希望二维的初步研究可给出较为系统的研究结果,并重点考察静电相互作用对不同组分的相溶性的影响.

2 模型与方法

2.1 理论模型

本文的模型为二维两组分带电囊泡.假设其周长L固定,且局部近似不可压缩,故线元亦假设固定不变.该囊泡由两种不同磷脂组成,组分A带负电,组分B电中性.由于这两种组分在囊泡上可以自由迁移,故若相容性不佳时则会产生相分离,导致组分的分布变化及囊泡形变,如图1所示.

图1 两组分带电囊泡的形变耦合相分离示意图(a)相分离之前组分分布均匀;(b)相分离之后分成若干相区;其中红色部分为带负电荷的组分A,蓝色部分为电中性的组分BFig.1.Schematic diagram of the phase separation of the twocomponent charged vesicle:(a)The components are evenly distributed before the phase separation;(b)the phases are separated and divided into several phase regions.The red part is composed of the negatively charged component A while the blue denotes the electrically neutral component B.

2.2 模拟方法

本文主要结合离散空间变分方法[21]和耗散动力学方法[17]研究两组分带电囊泡.求解一个物理模型的动力学过程时,离散空间变分方法首先对这个模型的物理空间坐标进行离散,然后得到在离散空间坐标下的自由能泛函,再对离散的自由能做变分,直接得到已经离散好的差分方程,最后再利用这些差分方程去模拟具体的物理模型[21−23].Li等[24]将此方法引入生物膜的理论研究,并将其应用于二维囊泡的相关模拟,得到了与其他参考文献报道相同的结果.此外,离散空间变分法与耗散动力学结合还可用于模拟三维囊泡[25].该方法的优点主要有:1)数值稳定性强、计算速度快,且得到的囊泡形状光滑;2)不需要提前假设囊泡对称性,因此可得到非轴对称的中间演化态以及较大的形变等.

据上述模型,该体系的自由能主要由两部分组成(F=F1+F2),其中第一部分为

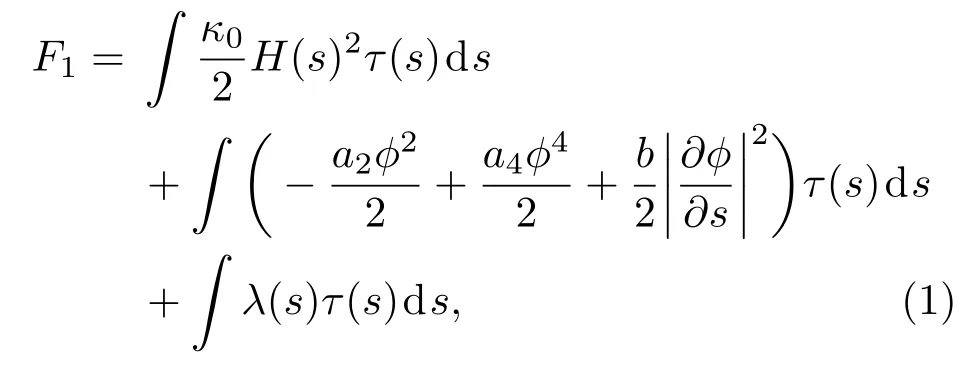
F1表示除去静电能以外囊泡自身的能量,右端第一项为Helfrich弯曲自由能[26],第二项为Ginzburg-Landau自由能[17],第三项中的拉格朗日乘因子λ(s)用于保证二维囊泡线元不可压缩.这里κ0为膜的弯曲刚性;H(s)代表膜上离散点s处的平均曲率;ϕ=ϕA(s)− ϕB(s)为组分序参量,ϕA(s)和ϕB(s)分别为组分A和组分B在离散点s处的体积分数;和a4为大于0的唯象系数,其中a2与温度相关,而a4本文中通常设置为0.2;b1/2正比于相界面宽度.

自由能的第二部分为静电相互作用,依据Debye-Huckel近似[18],静电排斥能F2为

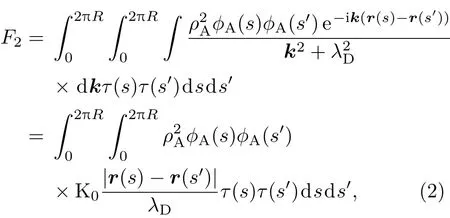
式中R为囊泡的初始半径,K0为0阶第二类修正Bessel函数;屏蔽长度λD可表示为λD=,其中ε为介电常数,e为单位电荷,n是溶液中电解质的浓度;ρA为带电组分A的电荷密度,囊泡所带的总电量Q=ρA〈ϕA〉L.

当静电屏蔽长度λD比较大(λD≥100 a,a为相邻两个离散点距离)时,静电能可简化为

为简单起见和减少计算量,只考虑静电屏蔽长度λD较大的情况.

体系中的总自由能为F=F1+F2,囊泡形变和A/B两组分的相分离可分别由下面的耗散动力学方程和TDGL方程描述[5,17]:

模拟过程中,上述两个动力学系数Lr和Lϕ皆设成1.0,时间步长通常为0.01.囊泡周长L=200 a离散成200个离散点,相邻两个离散点相距为a.初始形状皆为圆形,膜局部的A/B组分比等于平均组分比.

与前人的分子动力学的粒子模拟[20]相比较,上述方法具有以下优势和劣势:首先,相比之粒子模拟其计算量更小,容易得到系统性的模拟结果;其次,之前的分子动力学模拟一般主要用于考察形变动力学过程,而本文方法主要用于考察其平衡态形态;最后,上述方法存在其目前仍是一个二维模型的不足.

3 结果与讨论

3.1 典型动力学演化过程

图2给出了两组分带电囊泡一个典型的动力学演化过程,它分别展示了不同时刻囊泡形状以及A组分浓度分布.囊泡形态图中的红色代表带电组分(A)富集区,蓝色代表B富集区.具体参数设置见图例.

从图2可见,t=0时,带电组分A和组分B大致均匀分布于囊泡(各个离散点处ϕA=ϕB=0.5),故带电组分含量分布线呈现一条直线,此时囊泡呈圆形.由于此时初始组分浓度处于相图spinodal线之内,若不带电将发生spinodal decomposition相分离,从图2(b)—(d)发现,在此电量条件下,静电相互作用并没有完全改变相分离动力学的类型,动力学仍然沿spinodal decomposition进行.往后逐渐发生相区融合增长,最终囊泡形成了(6+6)个相区(图2(i)),即6个A组分富集区和6个B组分富集区,注意这些相区将不再继续融合,故由于静电的长程相互作用,使得两组分带电囊泡相分离呈现微观相分离.易发现,带电的组分A主要集中在弯曲的部分,而不带电的B组分膜显得平直.组分A集中在弯曲部分并不是因为带电导致A组分膜刚性变小了,相反因为静电排斥作用其表观刚性变大了;它弯曲是相对于组分B变得平直而言,而B组分变平直主要是因为不同带电A相区间的静电排斥作用所致,只有B组分变平直才可能使不同的带电A相区相互远离对方,以降低体系的自由能.

3.2 温度影响与相图

在Ginzburg-Landau自由能里,唯象系数a2与体系温度T有关(比如a2=c(T−Tc)),一般温度越高a2越小.我们通过改变a2研究温度对相行为的影响.

图3中蓝色曲线为电中性两组分囊泡上两组分序参数ϕ与唯象系数a2所组成的有序-无序相边界线,可由混合自由能密度对ϕ求极小得到.中间的U型区域为相分离形成的有序相区域,在此相区域囊泡通过宏观相分离分成两相;两边类似三角的区域为不发生相分离的无序相区域.观察蓝色的曲线可以得出如下结论:当a2较小时或温度较高时,两组分互溶性较好,无相分离发生;a2较大时或温度较低时发生分相.

图3中红色曲线为带电两组分囊泡模型中的有序-无序相分离边界线.由于电荷的引入,囊泡自身的静电排斥作用使囊泡上的电荷难以聚集,因此不利于相分离现象的发生,所以带电囊泡的有序相区域变窄了;相反地,静电相互作用增加两种组分间的互溶性.例如当a2=0.3时,对于非带电两组分囊泡而言,两组分的序参量(ϕ=ϕA(s)−ϕB(s))处于[−0.86,0.86]之间可以发生分相,而对于带电两组分囊泡而言,两组分的序参量处于[−0.67,0.67]之间才能分相.注意,与中性两组分相图不同,红色曲线左右并不完全对称(见3.3节讨论).

图2 带电两组分囊泡相分离随时间的演化过程(参数设置为L=200 a,a2=a4=0.2,κ=0.1kBT,ρA=−1.0 e/a2,〈ϕA〉= 〈ϕB〉=0.5,Q= −100 e/a)Fig.2.The dynamical evolution of phase separation of a two-component charged vesicle.Parameter setting:L=200 a,a2=a4=0.2,κ =0.1kBT,ρA= −1.0 e/a2,〈ϕA〉= 〈ϕB〉=0.5,Q= −100 e/a.

图3 非带电两组分囊泡与带电两组分囊泡的相图(参数设置:a4=0.2,L=200 a,κ=0.1kBT,ρA= −1.0 e/a2)Fig.3.The phase diagram of two-component electricalneutral vesicle and charged vesicle.Parameter setting:a4=0.2,L=200 a,κ=0.1kBT,ρA= −1.0 e/a2.

图4给出了带电组分含量〈ϕA〉=0.5(即序参量ϕ=0),a2分别为0.2,0.4,0.6,0.8和1.0时囊泡的相分离情况.囊泡上相区的数目随着a2的增加而增加.当a2为0.2时囊泡上分为(6+6)个相区;当a2为0.4时囊泡上分为(14+14)个相区;当a2为0.6时囊泡上分为(18+18)个相区;当a2为0.8时囊泡上分为(21+21)个相区;当a2为1.0时囊泡上分为(23+23)个相区.囊泡形状下方为囊泡所对应的带电组分的分布情况.当a2较小时,囊泡上的相区数目较少;随着a2的增加,囊泡上相区数目逐渐增多,相区尺寸变小.即温度的降低,使得相分离越来越呈现微相分离的趋势.

图4 不同唯象系数a2或温度对带电两组分囊泡相分离的影响(参数设置:a4=0.2,L=200 a,κ=0.1kBT,ρA= −1.0 e/a2,〈ϕA〉= 〈ϕB〉=0.5,Q= −100 e/a)(a)–(e)a2 分别为0.2,0.4,0.6,0.8和1.0Fig.4.In fluences of phenomenological coeffcient a2or temperature on the final con figurations of the two-component charged vesicle.Parameter setting:a4=0.2,L=200 a,κ =0.1kBT,ρA= −1.0 e/a2,〈ϕA〉= 〈ϕB〉=0.5,Q=−100 e/a.a2from(a)to(e)is set to 0.2,0.4,0.6,0.8 and 1.0,respectively.

图5 不同带电组分含量〈ϕA〉对两组分带电囊泡相分离的影响(参数设置:L=200 a,κ=0.1kBT,ρA= −1.0 e/a2,a2=a4=0.2,Q= −100 e/a)(a)–(j)〈ϕA〉分别为0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9和1.0Fig.5.In fluence of the charged concentration 〈ϕA〉on the phase separation.Parameter setting:L=200 a,κ=0.1kBT,ρA=−1.0 e/a2,a2=a4=0.2,Q=−100 e/a,〈ϕA〉from(a)to(j)is set to 0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9 and 1.0,respectively.

3.3 带电组分含量〈ϕA〉的影响

影响囊泡相分离的因素较多,例如:体系的温度、囊泡两组分含量之比、两相界面之间的线张力、自发曲率等.在图3相图中发现序参量ϕ绝对值越大(两组分的含量差越大)越难发生相分离.为进一步细致探究该因素影响,图5(a)—(j)分别考察囊泡中两组分含量之比分别为1:9,2:8,3:7,4:6,5:5,6:4,7:3,8:2,9:1和10:0的情形.

带电组分含量较低时(图5(a)和图5(b)),囊泡不发生相分离,所有的组分依然均匀地混合在一起;当两组分的比例为3:7时(图5(c)),囊泡开始发生相分离,此时生成(3+3)个相区域;当带电组分含量继续增加时,囊泡所形成的相区也越来越多,当带电组分含量与非带电组分含量相等(图5(e))时囊泡分为了(6+6)个相区;随着囊泡带电组分含量的继续增加,囊泡所形成的相区又相应地减少(图5(f)和图5(g));当带电组分的含量大于等于0.8时,囊泡便不再发生相分离行为.

注意到分相行为并不完全关于〈ϕA〉=0.5或组分比例(5:5)对称,比如当组分比例为4:6时呈现(6+6)相区,而在其对称组分比6:4则只有(4+4)相区.

3.4 带电组分电荷密度的影响

带电组分的电荷密度ρA也是影响两组分带电囊泡相分离的一个重要因素.相同带电组分含量的情况下,带电组分的电荷密度越大,囊泡上所带的总电量也就越大.表1列出了不同电荷密度下囊泡上的相区数目,表1中的编号(a)—(e)对应于图6(a)—(e).

表1 不同电荷密度ρA时囊泡的相分离情况Table 1.In fluence of charge densities.

图6 不同电荷密度下囊泡相分离的情况(参数设置为:L=200 a,κ=0.1kBT,a2=a4=0.2,〈ϕA〉= 〈ϕB〉=0.5,Q=−100 e/a)(a)–(e)ρA分别为−1.0 e/a2,−1.5 e/a2,−2.0 e/a2,−2.5 e/a2和−3.0 e/a2Fig.6.Phase separation of vesicles with different charge densities.Parameter settings:L=200 a, κ =0.1kBT,a2=a4=0.2,〈ϕA〉=〈ϕB〉=0.5,Q= −100 e/a,ρAfrom(a)to(e)is set to−1.0,−1.5,−2.0,−2.5 and−3.0 e/a2,respectively.

如图6所示,随着囊泡上带电组分电荷密度的增加,囊泡相分离形成的相区数目越多.但是在上述条件下,每个相区的带电组分含量(图6(f)—(j))有所降低.这是因为在相同带电组分含量时,随着电荷密度的增加,囊泡自身所带的电量越大,囊泡上自身的静电排斥作用也就越强,因此更倾向于形成更多的相区来减小自身的静电排斥作用.由于囊泡整体的带电组分含量不变,因此每个区域的带电组分含量也有所减小,所以带电组分含量的分布峰的高度随着电荷密度的增加(相区的增多)而有所降低.

4 结 论

本文用离散空间变分法结合耗散动力学对二维两组分带电囊泡相分离进行了系统的研究.主要考察了静电相互作用对两种组分表观相溶性的协调机制.发现当两种组分原本略微不相溶、但仍会发生同组分团聚或相分离现象时,静电相互作用可完全抑制相分离,避免同种组分的团聚;而当两种组分原本就较不相溶或温度较低时,静电相互作用会显著增加相区数目,使其呈微观相分离,从而避免了同种组分大范围的团聚.此研究结论定性地适用于三维两组分带电囊泡,并对理解一些生命现象有重要启发.

[1]Ouyang Z C,Helfrich W 1987 Phys.Rev.Lett.59 2486

[2]Lim H W G,Wortis M,Mukhopadhyay R 2002 Proc.Natl.Acad.Sci.USA 99 16766

[3]Mukhopadhyay R,Gerald L H W,Wortis M 2002 Biophys.J.82 1756

[4]Yang F Y,Halidan J M H,Jiang Z Y 2014 J.Atom.Mol.Phys.31 677(in Chinese)[杨方源,哈丽旦·居马汗,蒋中英2014原子与分子物理学报31 677]

[5]Li J F,Zhang H D,Qiu F 2013 J.Phys.Chem.B 117 843

[6]Liang X Y,Li L,Qiu F,Yang Y L 2010 Physica A 389 3965

[7]Li L,Liang X Y,Lin M Y,Qiu F,Yang Y L 2005 J.Am.Chem.Soc.127 17996

[8]Lipowsky R 1992 J.de Physique II 2 1825

[9]Jülicher F,Lipowsky R 1993 Phys.Rev.Lett.70 2964

[10]Leibler S 1986 J.Phys.47 507

[11]Seifert U 1993 Phys.Rev.Lett.70 1335

[12]Jørgensen K,Klinger A,Raiman M,Biltonen R L 1996 J.Phys.Chem.100 2766

[13]Jørgensen K,Mouritsen O G 1999 Thermochim.Acta 328 81

[14]Sunil-Kumar P B,Gompper G,Lipowsky R 2001 Phys.Rev.Lett.86 3911

[15]Yamamoto S,Hyodo S 2003 J.Chem.Phys.118 7937

[16]Laradji M,Sunil Kumar P B 2004 Phys.Rev.Lett.93 198105

[17]Taniguchi T 1996 Phys.Rev.Lett.76 4444

[18]Sinha K P,Thaokar R M 2016 Eur.Phys.J.E 39 73

[19]Li J F,Zhang H D,Qiu F,Yang Y L,Chen J Z Y 2015 Soft Matter 11 1788

[20]Ito H,Higuchi Y J 2016 Phys.Rev.E 94 042611

[21]Li J F,Zhang H D,Qiu F,Yang Y L 2005 Acta Phys.Sin.54 4000(in Chinese)[李剑锋,张红东,邱枫,杨玉良2005物理学报54 4000]

[22]Li J F,Zhang H D,Qiu F,Shi A C 2013 Phys.Rev.E 88 012719

[23]Guo K K 2005 Ph.D.Dissertation(Shanghai:Fudan University)(in Chinese)[郭坤琨 2005博士学位论文 (上海:复旦大学)]

[24]Li J F,Zhang H D,Tang P,Qiu F,Yang Y L 2006 Macromol.Theory Simul.15 432

[25]Xia B K,Li J F,Li W H,Zhang H D,Qiu F 2013 Acta Phys.Sin.62 248701(in Chinese)[夏彬凯,李剑锋,李卫华,张红东,邱枫2013物理学报62 248701]

[26]Helfrich W 1973 Z.Naturforsch.C 28 693