超声波电喷推力器羽流中和特性研究

于博 张岩 贺伟国 杭观荣 康小录 赵青

1)(电子科技大学物理电子学院,成都 611731)

2)(上海空间推进研究所电推进事业部,上海 201112)

3)(上海交通大学机械与动力工程学院,上海 200240)

1 引 言

近些年,随着器件小型化、集成化技术的快速发展[1−3],小卫星平台的研制已成为航天领域的重点研究方向之一,各类新型微推进技术也随之受到关注.其中,电喷推力器是利用带电流体在高强电场中的极化作用,形成类似泰勒锥几何结构[4]的发射液锥,在液滴的不断供给和发射的动态平衡下,完成带电液滴在真空中的发射,接着,在中和机理作用后,形成定向运动的中性液滴,提供推力.电喷推力器的功率一般在1—20 W,推力可以覆盖1—100µN不等[5,6],是应用于立方星平台的微推进技术[7].现今报道的绝大多数都是毛细孔电喷推力器[8−11]:包括传统的以离子液滴为工质、金属毛细孔电喷推力器[8],以液态碘为工质、硅发射体的毛细孔电喷推力器[9],外加磁场的铁磁体液滴电喷推力器[10],以及高液压通道的胶体电喷[11].以上胶体电喷的发射机理都是利用多孔隙中液体的毛细作用来提供形成泰勒锥的触发条件.由此,胶体电喷的推力密度和液滴形成太小会受限于多孔隙的加工情况,孔隙数量会受到加工空间和加工精度的限制,如果这些多孔数量较多,则加工时会影响到旁边孔隙,或是如果孔隙加工不均匀,发射液滴也会明显存在空间上的分布不均特性[12].因此,在2010年,有学者提出了一种推力密度更高的电喷推力器——超声波电喷推力器[12].

超声波电喷推力器是基于超声源对发射表面液体提供震动,形成液体表面规则的、阵列式的驻波[13,14].这些细微驻波的形成为带电液体形成发射泰勒锥提供了周期性的条件,即液滴的发射仅在波峰形成的一段极短时间内完成[12,15].近几年来,本团队人员对超声波电喷的研究都集中在驻波形成机理、带电液滴发射的验证等研究[12−15].然而,在2017年3月,以场发射阴极作为中和器进行性能试验时,发现了以下两个现象:1)推力与理论发射方向存在明显的3°—4°的夹角;2)推力器的阳极效率没有理论计算值(70%以上)[12,13]那么高,试验测得只有47%左右.面对上述问题,需要对超声电喷的液滴羽流中和过程进行研究,获得羽流的中和特性机理,以解答以上两个实际问题,以及对相应的优化策略给出参考.

针对超声波电喷推力器的羽流中和过程,采用试验方法的难度较高:1)探针介入测量会破坏羽流场的本身特性,影响试验结果的准确性;2)羽流的具体中和过程无法通过试验来进行细节上的捕捉,难以完成对中和机理的挖掘.因此,本文考虑使用数值计算方法来进行研究.首先,由于羽流中和过程是在电子与液滴间完成,这会涉及电子中和、液滴的流动与传热、液滴的破碎与重组等过程,故需要建立一种捕捉该过程的新算法——带电液滴中和模型(neutralization of electrons and charged droplets,NECD模型),具体将在第2节进行详细阐述;其次,在第3节,对该算法进行试验验证,介绍算法的计算精度和不足;第4节则对超声波电喷推力器羽流中和过程进行计算结果展示和分析,揭示出推力器的羽流中和特性;在第5节,对上一段中的两个问题进行解答,以及对超声电喷的性能设计给出相应的优化策略.

2 NECD模型

电喷推力器羽流的中和模型应具备捕捉正负带电粒子在中和过程中粒子的输运过程、碰撞过程以及液滴的破碎与重组等过程的能力,并且可以完成中和过程中各粒子的能量变化的追踪.因此,基于上述要求,输运过程的计算采用PIC(单元粒子)算法是比较合适的,以捕捉带电粒子在电场作用下的运动状态以及带电粒子的空间电势分布.PIC算法在大多数等离子体数值计算的文献中都有介绍[16,17],这里不再赘述.

除输运过程外,本文模型还应包括粒子间碰撞、液滴破碎、传热等过程的子模型.关于这些子模型,本节进行重点介绍.

2.1 电子-液滴碰撞过程

在讨论电子与液滴的碰撞时,分为两种情况:1)如果液滴带正电,电子与液滴的中和过程;2)如果液滴呈中性或负电,电子被液滴吸附过程.

需要说明的是,对电子-液滴碰撞的判断是基于对运动到网格内的电子,在当前网格内各物理参数制约下的碰撞概率判断.因而,在判断一个电子在液滴群内穿梭时,假设液滴可以作为背景气体存在,电子能否与液滴发生碰撞就是指在一个时间步长内,电子移动路径长度上是否包含一个电子平均自由程.

首先,一个时间步长内电子掠过的长度为

ve为电子运动速度(m/s),Δt为时间步长(s).

其次,电子在当前网格内运动的平均自由程由该网格的相关参数确定,有

其中,Rcell为该网格内液滴的平均半径(m),Ncell为该网格内液滴的数密度(m−3).

接着,对电子与液滴的碰撞进行判断:

1)如果电子掠过的路径大于等于当前网格内的平均自由程,则认为电子在该网格内触发碰撞,并将该时间步长内在此网格内发生碰撞的电子电荷对网格内所有液滴进行平均分配;

2)如果电子掠过的路径小于当前网格内的平均自由程,则认为电子有一定概率在该网格内发生碰撞,概率为

最后,对电子的能量沉积进行判断:

1)如果电子与正电液滴碰撞,则认为电子与液滴中和,并将全部电离能Eionization沉积给液滴转化为液滴的内能,提升液滴温度ΔTl(K)(ml为液滴质量(kg),cp为液滴比热容(J/kg·K)),

2)如果电子与中性或负电液滴碰撞,则认为电子被液滴吸附,不做能量变化处理,待到某时刻正负液滴发生中和时,再进行电离能的沉积处理,以此保证能量守恒.

2.2 液滴之间的碰撞过程

关于液滴之间的碰撞过程,采用基于蒙特卡罗的直接模拟(DSMC)算法[18]衍生出的算法.这一点与电子-液滴碰撞不同,是对液滴在网格物理参数制约下的判断.这里需要进行假设:忽略三个或以上的液滴碰撞事件,仅关注两液滴的碰撞事件.

首先,任意网格内,每个液滴在当前网格内发生液滴间碰撞的概率PNTC为

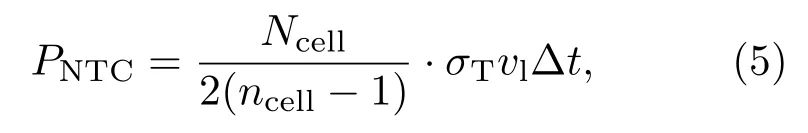
其中,ncell为当前网格内液滴的数量,σT为该液滴在当前网格平均液滴尺寸下的碰撞截面(m2),vl为当前液滴的运动速度(m/s).实际上,该公式是Bird[18]在计算稀薄等离子体流体时提出的重粒子间碰撞模拟的算法,通过粒子在一个时间步长内扫过体积的大小来判断粒子间的碰撞概率,这是一种基于对几何概型的统计算法,本文将这种思想应用在液滴碰撞的计算上.

与DSMC算法不同的是,(5)式是基于对单个液滴的碰撞概率为前提,而DSMC算法是对网格内每个碰撞对逐一进行判断,但是,(5)式从本质上与DSMC算法对碰撞概率的捕捉是一致的.

接着,碰撞截面σT为

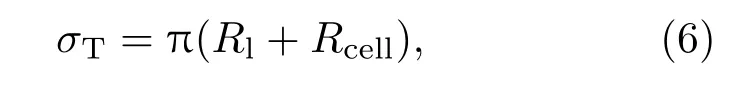
Rl为该液滴的半径(m).

两液滴碰撞后,可能会出现融合或反弹.Jayaretne和Mason认为[19],液滴的反弹主要发生在小尺度液滴对大尺度液面的碰撞中(例如液滴对水面或小液滴对大液滴),并且要满足一定的条件:R＞Eboun,其中R为(0,1)之间的随机数,Eboun为反弹效率.Eboun除了要考虑两个液滴的物理状态外,还要考虑两液滴的相对速度以及夹角.在推力器的羽流中,液滴的迁移方向几乎一致,速度矢量夹角较小,因此,Eboun几乎为0,可认为反弹发生概率极低,考虑到计算速度,本文予以忽略.

两液滴融合为一体,其运动状态由动量守恒来确定:

这里,对液滴中和过程的能量沉积进行判断:

1)如果碰撞发生在正负液滴之间,则将电荷绝对值较小液滴的电荷电离能(|qmin|Eionization)沉积给液滴转化为液滴的内能,提升液滴温度,

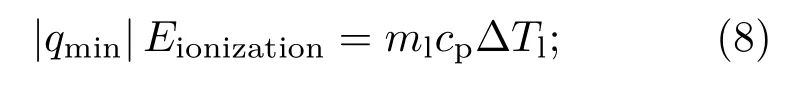
2)如果碰撞发生在同电荷液滴之间,则认为两液滴的电荷都保留给重组后的液滴,不做能量变化处理,待到某时刻再有正负液滴发生中和时,再进行电离能的沉积处理,以此保证能量守恒.

2.3 液滴的破碎过程

2.3.1 破碎触发的判断

液滴在气体中运动时,由于外力与内部张力的作用会在液滴表面形成一种对抗,当这种对抗没有打破维持液滴的平衡时,液滴可以保持原状态,当这种对抗已经足够打破这种平衡时,液滴就会发生破碎,这是一般情况下的液滴破碎.

然而,当液滴带有电荷,在静电场和压力场中运动时,则会受到电场力的作用,但是,在初期液滴破碎的判断中,液滴未形成尖端状的极化结构,故电场对液滴的破碎作用暂且不考虑,但是,在液滴破碎成小液滴时,电场力的作用就需要进行考虑.由此,运动液滴与背景气体发生相对运动时产生的冲击E1,液滴的表面张力维持作用E2.此刻,若后者大于前者,液滴可以在此刻保持不破碎:

其中,E2是维持液滴不破碎的能量(J),可描述为如下[17]:

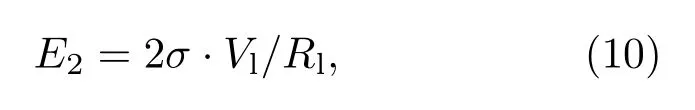
σ是水液滴的表面张力(N/m),Vl是滴液的当前体积(m3),Rl是滴液的当前半径(m).

接着,E1是气流冲击液滴所产生的能量(J),可描述为[20]

ρg为背景气体的密度(kg/m3),Δv为液滴与背景气体的相对速度(m/s),这里可认为是液滴的运动速度.

值得注意的是,水滴的表面张力σ是一个随温度变化的物理量,并且这种变化在本文的工况下是不可忽略的,尤其在多次进行中和过程的液滴,其温度的升高会影响表面张力的作用.因此,针对液滴的表面张力σ与液滴温度T,本文进行了公式耦合.图1显示表面张力随液滴温度的变化曲线以及耦合公式.由此,可根据液滴温度T直接求得当前液滴的表面张力.

图1 表面张力随温度的变化规律[21]Fig.1.Surface tension vs the droplet temperature[21].

2.3.2 液滴破碎后的处理

为实现计算中快速处理液滴破碎后的运动状态,本实验室特意对带电液滴在电场中的破碎过程进行了数值计算.计算模型可参考文献[22],其中,在连续性的控制方程中,源项改为网格节点极化电荷所受到的电场加速度极化电荷qplr是考虑分子内部电荷库仑作用下的节点电荷数量,这部分的处理方法在泰勒锥的模拟中[23]是比较常见的,这里不再赘述.

需要说明的是,如果电场均匀,带电液滴仅仅会表现为整体的迁移运动,只有当电场不均匀时,带电液滴才能够有被拉扯的作用,并且随着电场不均匀系数f(网格内最大电场强度Emax与平均电场强度Eave的比值)的增大,破碎将更加彻底,典型的计算结果如图2所示.在液滴破碎过程中,始终会受到气流冲击作用和不均匀电场的拉扯作用.在破碎最开始阶段,电场拉扯作用是可以忽略不计的,但是,随着液滴几何形状的拉伸,电场的拉扯作用将逐渐增强.这意味着一旦液滴开始进入破碎过程时,液滴将会在不均匀电场极化作用下加速破碎,迅速裂解为多个圆液滴或细长液滴,圆液滴由于表面张力重新占据优势而得到了维持,但细长液滴则会在电场极化作用下继续发生破碎,直到裂解成能够维持住的圆液滴为止.

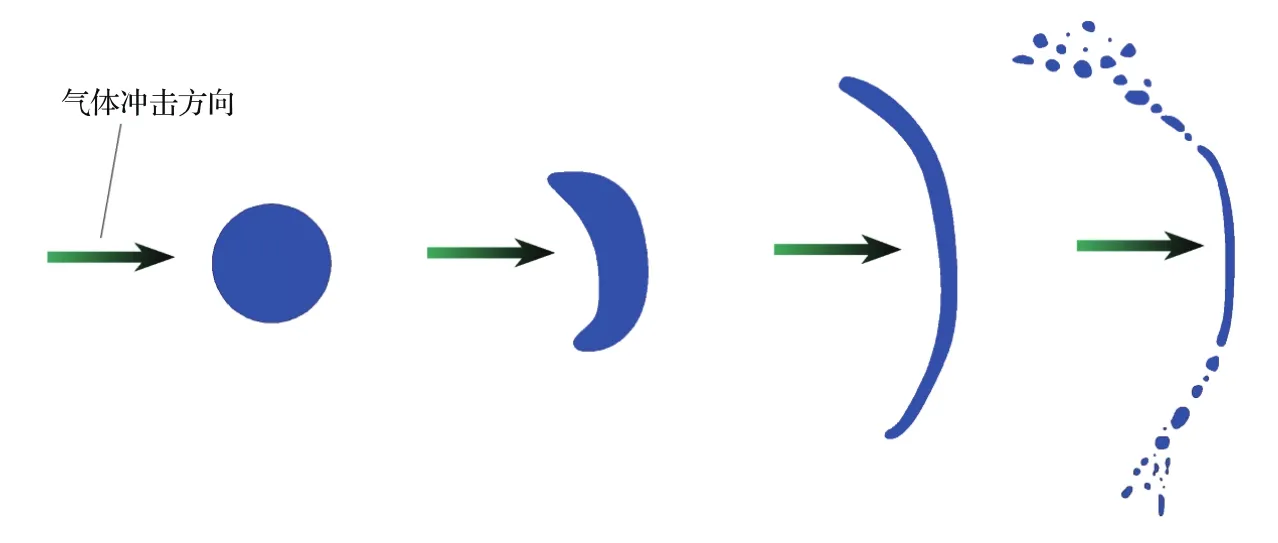
图2 液滴破碎过程模拟(液滴初始体积8.29×10−19m3,f=1.4,温度320 K)Fig.2.Simulation of droplet breaking up(droplet initial volume 8.29×10−19m3,f=1.4,temperature 320 K).

图3给出了液滴破碎更为细节的一系列数据,以便我们快速设定不同情况下的液滴的破碎后的状态.这里需要说明的是,本文这种快速判断方法是针对羽流多物理过程的复杂性,为提高计算效率而采取的粗糙、简略方法,并没有实现逐个液滴破碎过程的判断.

然后,当液滴破碎发生后,对液滴破碎的能量耗散进行统计:首先,原初液滴的表面张力能会小于各破碎后小液滴的表面张力能之和,这样才能够维持小液滴不破碎;接着需将两者张力能的差值,即小液滴的动能损失量之和,平均分摊到各个液滴.

其次,根据数值计算,液滴运动速度的角度变化不会超过10°,因此,针对每个破碎后小液滴的运动速度角度变化取−10°—10°之间的随机值,液滴总质量也采取平均分配.

图3 不同电场不均匀系数、不同液滴温度下的液滴破碎计算结果Fig.3.Calculation results of the droplet breakage at different local f and droplet temperature.

需要补充的是,在数值计算中,液滴的破碎是瞬间完成的,破碎后的所有小液滴暂时共用同一个空间坐标,但由于各个小液滴的随机运动方向不同,会在下一个时间步长分散开.

2.4 液滴与背景气体的传热和流阻过程

如前所述,液滴温度的升高主要源于中和过程带来的电离能沉积,大量电离能沉积在液滴,必然导致液滴温度升高,当液滴温度高于背景气体温度时就会产生与环境的传热,这个过程涉及到表面热辐射和对流换热.但值得说明的是,周围环境温度和液滴温度相差很少,辐射换热的热流密度将远远小于对流换热产生的热流密度,两者会相差2—3量级,故这里仅考虑背景气体对液滴的对流换热作用,以此作为液滴降温的主要途径.

液滴在运动中,受到冷却作用的降温功率(W)为

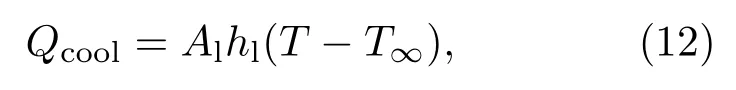
其中,Al为液滴表面积(m2),hl为液滴与当地背景气体的表面换热系数(W·m−2·K−1),该参数与液滴的运动速度有关,T∞为当地背景气体温度(K).

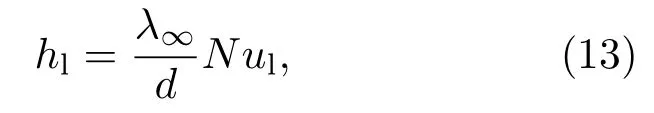
λ∞为背景气体的导热系数(W·m−1·K−1);d为液滴的特征尺度(m),对于球体,取半径的1/3;Nul为努赛尔数.

液滴运动中由于气体的冲击是变形状态的,但这里假设液滴形状为刚性球体,采用流体外掠圆球的模型[24],那么努赛尔数Nul可以表示为

其中,Re为雷诺数,Pr为普朗特数,两者均属于无量纲数;η∞和ηl分别为以背景气体温度和以液滴温度来计算的动力黏度(N·s·m−2).

由于液滴特征尺寸较小,在102m/s量级的运动速度下,雷诺数Re极小,因此,这里考虑采用低雷诺数下的刚性球体的阻力计算公式[25]:

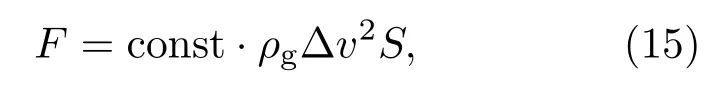
其中,const为表征物体形状的常数,球体取0.4—0.5,根据文献[25],在低雷诺数下,const取0.5为宜;S为液滴球体的横截面积(m2).

3 验证试验

为验证NECD模型的正确性,开展超声波电喷推力器的羽流中和试验,采用推力测量仪器进行推力的测量,采用高速相机对液滴大小进行测量,并且以上述两者和计算结果进行比对来验证模型的计算精度.需要说明的是,推力值的验证目的是验证液滴输运过程的计算精度,即以大量运动液滴所形成的推力来衡量液滴运动速度的捕捉精确程度;液滴粒径大小的验证目的是验证液滴输运过程中破碎与重组的捕捉精确程度.那么,通过以上两项验证,基本可以实现NECD模型的计算精度评估.

试验系统图如图4所示:超声波电喷推力器固定于转动机构的右侧托板上,托板则由三根支撑柱进行固定,并且上下支撑柱可以自由伸缩,中间的支撑柱与托板由转动节点连接,可以令托板在−15°—15°之间进行转动,由此调整推力器的羽流喷射方向.

图4 验证试验系统示意图Fig.4.Schematic diagram of the experiment system.

需要说明的是,本文没有采用传统的推力架来进行推力的测量,原因如下:超声波推力器中的超声波发生器对推力测量系统有很大的震动影响,导致测量结果波动极大,本文曾经测量过推力器正常工作时的推力,然而,测量结果在0.1×10−6N—80×10−6N之间不稳定振荡,已经无法获取准确数值.

所以,本文采用“打靶法”的测量思路.“打靶法”推力测量系统由悬臂薄板、电涡流传感器和示波器组成.首先,提出轴向有效推力的概念,即羽流产生实际推力矢量在推力器设计中心轴线方向上的分量,为该推力器的轴向有效推力.那么,推力测量系统测得的推力实际上是有效推力,而不是推力器的真实推力,因为任何推力器的推力方向与中心轴线(设计方向)都存在微小偏角.于是,有效推力为F0的羽流对悬臂薄板会产生一个冲击力P,以P来描述F0,有

其中,sinβ为羽流对悬臂薄板产生的冲击形变角度,由于推力较低,β一般可认为是90°;冲击力P会对悬臂薄板产生一个微小位移d,有

其中,E为悬臂薄板的弹性模量(MPa),w为薄板的横向宽度(m),t为薄板的厚度(m),L为薄板的纵向长度(m).那么,只要测得位移d的数值,就可以推导出有效推力F0.而电涡流传感器正是用来测量微小位移的装置,传感器利用感应线圈来产生感应电流,感应电流与位移d的大小有关,由此,传感器可以将位移的大小转化为电流的高低来读取位移d的数值.传感器的性能参数如表1所列.

表1 电涡流传感器技术指标Table 1.Technical parameters of the eddy current sensor.

需要说明的是,由于超声波羽流的波动以及放电振荡等因素的影响,由传感器所读取的电流数据实际上是一个范围,例如,工况2所测得的电压值为4.1 mV—8.9 mV,本文取平均值来表示实际值,即电压值为6.5 mV,所测推力为15.2×10−6N.

图5 液滴粒径的测量方法Fig.5.Measuring method of the drop diameter.

此外,在正常布置试验系统时,会将推力器中心轴线与悬臂梁板垂直放置,但由于推力器偏角的存在,所测得的推力F1一定是偏小的;那么,在不断调整转动机构时,一定存在一个转动角度θ,使得此刻测得的推力值Fmax为最大.那么,可认为F1/Fmax的反余弦值为推力偏角.事实上,推力偏角与转动角度θ有差别,本文以羽流达到悬臂薄板时的推力状态为准,所以推力偏角不采用转动角度θ.

最后,液滴的粒径由高速相机来进行测量,由于液滴具有一定的运动速度以及粒径在的10−6m的尺度,拍摄到清晰照片的难度较高.因此,本文采取一个对相片做后处理的方法来获取液滴的粒径,如图5所示.

3.1 推力的验证

试验输入条件设置见表2.在表2参数条件下,测量出三组推力,与相应工况的计算结果进行比对,见图6.

根据图6对于推力计算的相对误差在16%左右,推力偏角的计算误差在22%左右,并且随着工况的变化,变化趋势上可以保持一致.图6仿真结果表现出高于试验结果,推测是由于空间电势求解模型和破碎模型的误差放大了羽流电荷分布的不均匀性,导致推力偏角的升高.

表2 各工况的输入参数Table 2.Parameters of the test operation in different cases.

图6 推力测量的试验与计算结果对比Fig.6.Comparison of the thrust between the test and calculation results.

3.2 液滴粒径的验证

为验证液滴粒径的计算结果,首先对不同位置的羽流进行了高速相机的拍照,获取3组典型位置下的液滴照片,如图7所示,各照片中,按照液滴从小到大的顺序进行了编号,图中参数l为与羽流来流面的水平距离(该距离最大为3 m).

图7 不同羽流位置的液滴照片 (a)l=0.3—0.31 m;(b)l=1.50—1.51 m;(c)l=2.70—2.71 mFig.7.Photos of droplets in different plume position:(a)l=0.3—0.31 m;(b)l=1.50—1.51 m;(c)l=2.70—2.71 m.

接着,在每一处羽流位置上,从计算结果中抽取10个液滴,以清晰度较高的液滴为优先,这样的抽取方法确实受到了相机性能的限制.依然按照从小到大的顺序编号,以液滴粒径的计算值与试验值进行对比,对比的结果见图8.虽然计算结果与试验结果有误差不可避免,但在不同羽流位置上的变化趋势可以保持一致.

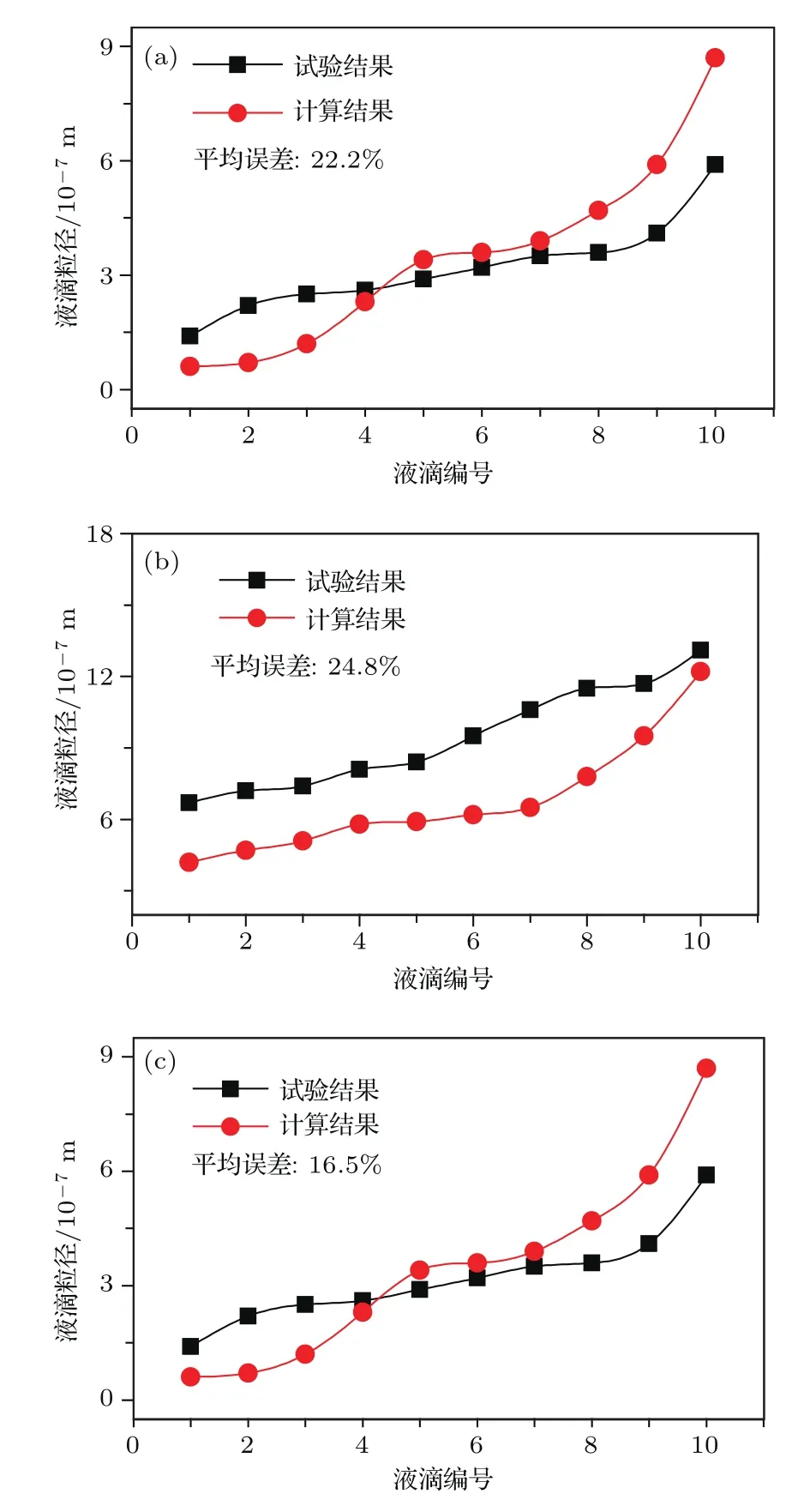
图8 液滴粒径的试验值与计算值的对比 (a)l=0.3—0.31 m;(b)l=1.50—1.51 m;(c)l=2.70—2.71 mFig.8.Comparison of droplet diameter between the test and calculation results:(a)l=0.3—0.31 m;(b)l=1.50—1.51 m;(c)l=2.70— 2.71 m.

至此,通过对推力、液滴粒径大小的验证,认为该模型的综合计算误差在20%左右,在趋势上可以与试验结果保持一致,可满足定性分析的需要.但定量计算精度并不算很高,原因为模型本身所考虑的子模型较多,进行了多项假设.这里,对NECD模型影响精度的一些重要假设进行了归纳:

1)电子与液滴碰撞时,电荷对网格内液滴平均分配的假设;

2)忽略三个或三个以上液滴碰撞的假设;

3)对液滴破碎后的状态进行快速判断的假设;

4)对运动中液滴的传热与流阻计算采用刚性球体的假设(液滴运动时存在一定的形变).

上述假设都是提高计算效率所必要采取的措施,但即使这样,采用16线程、32 GB内存的服务器,计算一个算例依然需要100 h以上.实际上,它们确实对计算精度产生了相当大的影响,尤其是第3)项假设.然而,若未来计算机的计算速度大幅度提高时,可以对上述假设进行更精细化的处理,以此提高此模型的计算精度.

4 计算结果与分析

为解释前文提出的推力偏角和能损耗较高的问题,本节首先给出液滴的电荷密度、数密度以及速度分布的云图,以此说明液滴产生推力偏角的原因;接着,给出说明液滴破碎与重组情况的液滴体积分布和液滴温度分布云图,以此说明液滴产生巨大能耗的原因.最后,总结出超声波电喷推力器羽流的带电粒子中和的规律.计算的输入条件见表3.需要说明的是,计算区域覆盖径向(X方向)0.36 m,轴向(Z方向)3 m的范围,而羽流区域仅在计算域中X=0.09—0.27 m之间.

超声波电喷推力器的羽流中和过程比较特殊:液滴的碰撞截面较大,很容易将大多数的电子拦截下来,因此,正负电荷的中和过程会表现出一定的不均匀性.如图9所示,在左侧最接近阴极的位置,羽流上部分的带电量会迅速下降;接着会有大片的液滴逐渐由正电荷过渡到中性,再过渡到负电荷,出现了过量中和的特点,如图9的蓝色区;而距离阴极较远的羽流下部分会表现出中和较慢的现象,依然保持一定的正电性.

表3 计算输入条件Table 3.Input conditions of the calculation.

图9 液滴电荷密度分布云图Fig.9.Distribution contour of the droplet charge density.

在推力器的中和过程中,只要液滴从加速电极运动出,就会从加速阶段转变为减速阶段,开始进行动能对电势能的返还,但如果尽早与电子中和,则会不受电场的影响而保留动能继续运动,形成最终的推力.因此,在图9的结果下,由于过度中和效应,羽流上部分的液滴将具有更高的动能,如图10所示,羽流上部分的液滴速度将比下部分高很多.

同时,液滴运动越快的位置,数密度将越低,反之数密度将越高.因此,图11从侧面显示了羽流上下部分的液滴速度和数量的不一致,进一步证明了羽流中和的不均匀性.

图10 液滴速度分布云图Fig.10.Distribution contour of the droplet velocity.

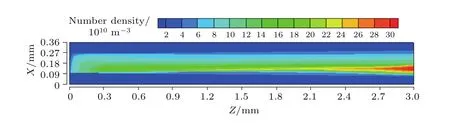
图11 液滴数密度分布云图Fig.11.Distribution contour of the droplet number density.

因此,在图9—图11的计算结果中,可以推导出羽流在中和过程中所形成的推力并不与液滴运动方向完全一致,而是会形成一个与阴极中和器背离的偏角.

接着,给出液滴在羽流输运过程中的能耗统计,见表4.

表4 羽流输运中的各类能耗比例Table 4.Each energy loss proportion of the plume.

这里,热损耗主要是指高温液滴与环境气体之间的对流换热损失;液滴破碎能耗是指一个大液滴破碎成小液滴后,总表面张力能上升而导致动能下降的损失;流动阻力损耗是指高速液滴受到大气阻力的能耗;弹性碰撞损耗是指不同速度方向的液滴在碰撞后,由动量守恒所导致的动能损失.需要说明的是,计算得到的总功率损耗(42.63%)与试验结果(53%)依然有偏差,除了计算模型的误差外,推测可能与阴极针通过遂穿效应发射电子和发射表面通过泰勒锥发射正电液滴所需要的电场做功并未考虑在本计算模型中有关.

进一步地,推力器能效较低的主要原因是液滴破碎发生频率较高,故讨论其内在机理:在羽流中和与输运过程中,液滴主要会由三方面的因素来影响破碎:1)较高的运动速度;2)较高的液滴温度;3)较明显的电场不均匀程度.

而在阴极中和位置处羽流区域的液滴速度较羽流中后部较高(此为因素1),并且液滴发生电子中和较为集中,电离能沉积导致温度高(见图12)(此为因素2),此外,该区域空间电荷的变化而导致电场变化极快,电场比较不均匀(此为因素3).因此,在阴极出口位置处的羽流区会形成破碎最容易、也是最集中的区域,这也是羽流产生如此多液滴破碎的主要原因,如图13的羽流前部分,单个液滴的平均体积出现急剧下降.此外,图13的羽流中后部的云图揭示:正负带电液滴的重组过程也伴随着少量的破碎,但多数液滴的体积是在逐渐增大的,依然以重组过程为主.

图12 液滴温度分布云图Fig.12.Distribution contour of the droplet temperature.

需要说明的是,液滴破碎是基于推力器羽流中和过程的特殊性而存在的固有过程:1)存在中和就涉及中和能的沉积,就会导致液滴温度的剧增;2)要保证推力性能就必须保证液滴具有相当的速度;3)中和集中的区域始终是电场不均匀性最强的区域.基于这三点因素,液滴破碎的能损很难降低到较小的水平,对于工质水来说,通常都在20%之上.

综上所述,可见超声波电喷的羽流中和过程是非常特殊、复杂的物理过程,隐含典型的电子-液滴的中和特性,不但涉及带电粒子的输运、碰撞,还涉及液滴的破碎与重组,以及传热过程.图14对超声波电喷推力器的羽流中和特性进行了概述:在羽流靠近阴极出口区域,发生正负电荷中和以及电子吸附过程,一方面,由于中和的不均匀性,表现为上部羽流呈负电性,下部羽流呈正电性,导致羽流上下部分的液滴运动速度不一致,会造成推力偏角;另一方面,由于靠近阴极出口的羽流区液滴的中和能沉积较大,液滴运动速度较快,是液滴发生破碎的集中区,大量破碎过程导致了较高的能量损耗,但在随后的羽流输运过程中,液滴的速度、温度逐渐过渡到较低的水平,因而在羽流中后部分,主要发生液滴的重组过程.

图13 单个液滴体积的平均值分布云图Fig.13.Distribution contour of the mean volume of one droplet.

图14 超声波电喷推力器羽流中和特性示意图Fig.14.Schematic diagram of the neutralization characteristics in UAET plume.

5 结 论

本文揭示了超声波电喷推力器的羽流中和过程中的各种物理机理内涵,在工程意义上,为推力器工作性能的优化提供了一定的参考;同时,在学术意义上,揭示出电子-液滴的中和特性与电子-离子中和特性截然不同,表现出多种物理过程耦合的复杂特性,为其他与电子-液滴中和相关的机理研究提供了参考理论.主要结论如下:

1)超声波电喷推力器羽流的中和过程会存在较高的电荷分布、速度分布的不均匀性,这是引起推力偏角的直接原因;

2)超声波电喷推力器的功率损耗主要集中在液滴破碎和热流失两个方面,其中,以液滴破碎所占比例最大,对于水工质来说,能耗通常在20%以上.

进而,本文对超声波电喷推力器的后续研发给出一些启示:

A)若采用电子中和器,可在其他方向进行对称布置,以此改善羽流中电荷的中和不均匀性,或者采用两台发射液滴带电性相反的推力器进行互和,但上述中和策略对两种推力器的性能一致性要求较高;

B)为提高推力器的能效,从降低液滴破碎频率的角度来说,可降低发射液滴的粒径或者更换表面张力系数较大的工质,但这样的设计需要对液滴发射装置进行相匹配的改进.

[1]Zhao Q,Huang X P,Lin E,Jiao J,Liang G F,Chen T 2017Opto-Electronic Engineer.44 140

[2]Jiao J,Zhao Q,Li X,Liang G F,Huang X P,Luo X 2014Opt.Express22 26277

[3]Zhao Y,Huang C,Qing A Y,Luo X 2017IEEE Photon.J.99 1

[4]Taylor G 1964Proc.Roy.Soc.Lond.A280 383

[5]Romero S,Bocanegra R,Gamero C 2003J.Appl.Phys.94 3599

[6]Lozano P,Martinez S 200541st Joint Propulsion Conference&ExhibitTuscon,Arizona.July 10–13,2005 p1

[7]Ober S,Branam R,Huffman R 201149thAIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace ExpositionOrland,Florida,January 4–7,2011 p1

[8]Legge R,Lozano P 2011J.Propuls.Power27 485

[9]Reading C,Anderson J,Kubiak C,Greer F,Rouhi N,Wilson D,White V,Dickie M,Mueller R,Singh V,Mackie W,Wirz R,Castano M 2016AIAA Propulsion and Energy ForumSalt Lake City,UT,July 25–27,2016 p1

[10]Kurt J,Lyon B 201652nd AIAA/SAE/ASEE Joint Propulsion ConferenceSalt Lake City,UT,July 25–27,2016 p1

[11]Gutierrez E,Castano M 2017J.Propuls.Power33 984

[12]Song W D,Shumlak U.2010J.Propuls.Power26 353

[13]Dong L,Song W D,Kang X M,Zhao W S 2012Acta Astron.77 1

[14]Zhang Y B,Hang G R,Dong L,Kang X M,Zhao W S,Zhang Y,Kang X L 2016Chin.Space Sci.Technol.36 9(in Chinese)[张姚滨,杭观荣,董磊,康小明,赵万生,张岩,康小录2016中国空间科学技术36 9]

[15]Kang X M,Dong L,Zhao W S 2014Acta Astron.98 1

[16]Passaro A,Nania F,Vicini A 200637th AIAA Plasmadynamics and Lasers ConferenceSan Francisco,California,June 5–8,2006 p1

[17]Robert S,Eduardo A 200945th Joint Propulsion Conference&ExhibitDenver,Colorado August 2–5,2009 p1

[18]Bird G 1963Gas.Phys.Fluids6 1518

[19]Jayaratne O,Mason B 1974Proc.Roy.Soc.Lond.380 218

[20]Luo T Q,Wang X Y,Zheng J Q,Wang Z T,Mao H M 2007Drainage and Irrigation Machinery25 57(in Chinese)[罗惕乾,王晓英,郑捷庆,王贞涛,毛惠敏2007排灌机械25 57]

[21]Gao S Q,Liu H P 2010Capillary Mechanics(Beijing:Science Press)p60(in Chinese)[高世桥,刘海鹏 2010毛细力学(北京:科学出版社)第60页]

[22]Cai B,Lee L,Wang Z L 2003J.Engineer.Thermophys.24 613(in Chinese)[蔡斌,李磊,王照林2003工程热物理学报24 613]

[23]Higuera F 2003J.Fluid Mech.484 303

[24]Yang S M,Tao W Q 2006Heat Transfer(4th Ed.)(Beijing:Higher Education Press)p258(in Chinese)[杨世铭,陶文铨2006传热学(第四版)(北京:高等教育出版社)第258页]

[25]Landau L(translated by Lee Z)2013Fluid Dynamics(5th Ed.)(Beijing:Higher Education Press)pp201–202(in Chinese)[朗道L著 (李植 译)2013流体动力学(第五版)(北京:高等教育出版社)第201—202页]