层结环境中浮力羽流的质量输移过程

赵 亮， 张 巍， 贺治国,2， 谈利明， 蒋后硕

(1. 浙江大学 海洋学院, 浙江 舟山 316000； 2. 国家海洋局第二海洋研究所, 杭州 310012； 3. 伍兹霍尔海洋研究所, 美国 伍兹霍尔 02543)

浮力羽流指在不同流体介质中受浮力驱动的柱状流动形态[1].在自然环境及工程应用中普遍存在着浮力羽流运动形态，如火山喷发形成的气流、火箭喷射出的高温气流、汽车尾气、烟气羽流、深海热液羽流等.浮力羽流在运动发展过程中不断夹带周围环境流体并发生物质交换，引起的物质输移对周围环境具有重大影响：火源上方形成的烟气羽流在火灾科学中为一重要概念，其输移质量决定了烟气生成量，是防排烟工程中的重要参考量[2]；深海热液羽流运动过程中伴随的质量输移对海洋的物质循环和生物活动有重要影响[3]，喷射时携带大量矿物粒子与金属粒子，这些粒子少部分直接在喷口附近沉积，大部分则随着羽流运动到一定高度并向周围扩散，参与大洋物质循环[4].

国内外对于浮力羽流已形成完备的理论体系，且有充足的数值模拟和物理模型实验作为支持[5-10].Morton等[5]在1956年提出经典MTT模型(以Morton、Taylor和Turner首字母命名)，给出了层结环境中点源浮力羽流的流场解析解，并详细分析羽干卷吸过程，不仅适用于热液羽流，而且适用于气相羽流等大多数流态.魏文礼等[6]采用欧拉双流体模型和混合模型结合标准k-ε紊流模型研究气泡浮力羽流的动力特性，认为欧拉双流体模型的结果更优.何标等[7]采用大涡模拟对气体羽流分层特性进行数值模拟，发现密度较小的组分主要分散在空间上部80%的范围内.Pham等[8]应用二维及三维粒子图像测速(PIV)技术研究纯羽流，观测到羽流的涡结构，揭示了其在卷吸过程中的作用.Han等[9]同样采用PIV技术测得伴随反应发生的羽流流场，并指出反应放热会降低羽流的卷吸速率.Mirajkar等[10]研究层结环境中浮力羽流的扩散过程，并且建立了羽流横向扩散速度随时间的变化关系.目前，对于层结环境中浮力羽流所引起的质量输移还有待深入研究，而密度层结是常见的羽流发生环境，尤其在海洋环境中.

本文通过层结盐水发生装置，在静止的线性密度层结盐水中开展一系列浮力羽流实验.采用时间解析PIV技术获得羽流的时空高分辨率流场，通过计算羽流的卷吸系数及垂向质量通量，定量分析羽流在演化发展过程中所产生的质量输移过程；提出了羽流最大输移质量计算公式并通过实验数据进行验证，为进一步深入研究自然界及工程活动中的羽流过程所产生的物质输运与混合奠定了理论基础.

1 实验方案与研究方法

1.1 实验装置

基于“双缸法”[11]，采用课题组前期搭建的层结盐水发生装置[12]，在有机玻璃实验水槽(50 cm×50 cm×50 cm)中生成稳定静止的线性密度层结盐水.实验时将喷口垂直向下固定在水槽正上方中心位置，并通过以高密度盐水从顶部向下注入线性层结盐水的办法，进行浮力羽流实验.实验水槽中线性层结盐水深度为47 cm，喷口位于水面下3 cm(图1).实验时浮力羽流的运动方向虽然与实际情况相反，但两者等效驱动力与运动方向一致，即两者动力学过程相同，浮力羽流的射流方向并不会影响其流体动力学过程[13-14].

应用PIV获得浮力羽流发展与演变过程中的可视化二维图像及流场，解析流场的演变过程.PIV系统分为图像采集与数据后处理系统两部分，其中图像采集系统由激光器和高频相机组成.实验采用连续波(波长532 nm，激光源功率10 W)垂直照射实验水槽的侧表面，形成厚度约3 mm的薄光面，使之经过喷口中心线，即通过羽流的中心线.在实验水槽正前方布置高频CMOS相机(采样频率200 帧/s)，相机采用16 mm F2.0 镜头，在垂直方向z-y平面28 cm(z)×21 cm(y)范围内获取羽流发展的二维可视化图像，坐标及示意图如图1所示.采集的PIV图像分辨率为 2 320 像素×1 726 像素，8 bit灰度图；添加到喷口射流盐水及密度层结盐水的PIV粒子直径15 μm，为与盐水密度相近的尼龙微粒，质量浓度3%(图2).需要指出的是，本文浮力羽流在达到充分演化发展时尺度均不超过实验水箱尺寸的3/4，即羽流到水槽底边界及边壁的距离均超过实验水箱尺寸的1/4，因此边界影响较小，可以忽略边界效应[8,14-15].采用PIV通用后处理软件对羽流二维图像进行处理，算法为多通迭代法，诊断窗口尺寸为32像素×32像素，初始与最终诊断窗口的重叠区为50%.获得流场数据后，再通过MATLAB进一步分析数据.

图1 实验装置示意图Fig.1 Experimental setup

图2 PIV采集的原始图像(工况10)Fig.2 The initial image collected by PIV (Case 10)

1.2 工况设计

浮力频率(N)定量表征环境的密度层结性，初始浮力通量(B)为喷口入射条件的度量，两者是浮力羽流的基本参数.计算表达式分别为

(1)

(2)

式中：g表示重力加速度；ρ0表示喷口出流盐水密度；ρa表示与喷口处于相同高度的周围环境盐水密度；ρb表示水槽底部的环境盐水密度；Q表示喷口出流盐水的体积通量(喷口流量)；∂ρ1/∂z表示层结环境的密度梯度.表1所示为根据N、Q、ρ0和喷口直径d等参数，设计的18组不同的实验工况.

表1 实验工况相关参数Tab.1 Experimental parameters

在实验水槽的壁面等较深位置处布置8个针状采水器(分别距离底部0、6、12、18、24、30、36、42 cm).在线性密度层结形成后， 羽流实验开始前， 抽取少量水样，确定羽流发生环境的盐度分布，并根据状态方程[16]计算盐水密度.应用最小二乘法对各组工况的盐水密度随水深分布进行线性回归分析，保证浮力羽流的发生环境具有良好的线性层结性[12].

1.3 参数计算方法

所有实验工况中，CMOS相机记录的羽流演变发展持续时间约为50 s.羽流在发展过程中的瞬时流速具有随机波动性，已有研究[17]指出：当羽流演变发展至某一时刻t*后，羽流流场便会达到稳定阶段，t*为与N相关的浮力时间尺度，且t*=2π/N.对于所有实验工况，在3t*≤t≤5t*稳定阶段，由羽流瞬时流场数据计算得到羽流时均速度场：

(3)

式中：U和W分别表示时均速度场水平(x轴)和垂直(z轴)方向速度分量；u和w分别表示通过PIV后处理得到的瞬时速度场水平和垂直方向速度分量；符号〈〉表示对所有瞬时速度场进行时间平均处理.通过得到的羽流速度场计算卷吸率和输移质量，定量研究浮力羽流的质量输移过程.

1.3.1卷吸系数 卷吸率指一种流体在运动过程中吸入另一种流体的速率，通常用卷吸系数α表示.卷吸过程是羽流在演化发展过程中产生物质输移的根本原因.对于单喷口浮力羽流，卷吸系数的计算表达式为：

αe=uh/ve

(4)

式中：uh表示羽流边界处的水平速度分量；ve表示同一高度处的羽流最大垂向速度分量.

经典MTT模型理论[5]认为：对于单喷口浮力羽流，卷吸作用主要发生在羽干处；对于羽干同一高度zk处的羽流质点，其垂向速度分量W(x,zk)呈现高斯分布.

W=Wme-(x-xm)2/b2

(5)

式中：Wm表示位于(xm,zk)处羽干中线的最大垂向速度分量；b表示位于高度zk处的羽干半径.

羽流在发展阶段，羽干半径b与羽流高度呈线性相关，即

b=cz+b0

(6)

式中：b0为截距常数；斜率c表示羽干半径的垂向变化梯度-db/dz，与αe关系如下[18]：

αe=5c/6

(7)

利用b随羽流穿透距离z的垂向变化梯度计算羽流的卷吸系数αe.由式(6)和(7)可得：

(8)

1.3.2垂向质量通量 浮力羽流在对于海底成矿、海洋勘探等具有重要影响.其输移质量可通过垂向质量通量M来表示为[17]

(9)

式中：r表示圆柱坐标系中的羽流水平半径，且最大值rmax=b；ρ表示羽流密度.

2 实验结果与分析

2.1 卷吸过程

为了便于显示，将羽干平均分成11层，采用式(5)对每层羽流垂向时均速度分量进行曲线拟合(图3)，从而得到b，再通过有限差分法计算-db/dz，由式(8)计算得到αe.羽干各层垂向速度分量的拟合结果如表2所示，羽干的垂向时均速度分量符合高斯分布，表明本文实验满足MTT模型卷吸理论中关于羽干垂向速度分布的假设.

采用文献[12]中的方法确定本实验中羽流的最大穿透距离Zmax，并将其作为无量纲化参数，对羽流垂向穿透深度z进行标准化处理.所有工况的卷吸系数随标准化穿透深度的平均分布曲线如图4所示.αe随着穿透距离明显变化：从喷口原点至z≈-0.3Zmax，αe逐渐增加；z≈(-0.3～-0.5)Zmax处，αe在 0.11 附近稳定波动，该段深度对应羽干区；之后，αe从z≈-0.5Zmax处的 0.1 减小至在z≈-0.7Zmax处的0，此处对应中性浮力层[12]，即羽流主要向周围扩散，而卷吸过程相对较弱；在z≈(-0.7～-1)Zmax处，αe为负值，这段深度对应羽帽区[17].本实验得到的羽干区卷吸系数为 0.09～0.13，与文献[17]范围相一致，表明了可靠性.

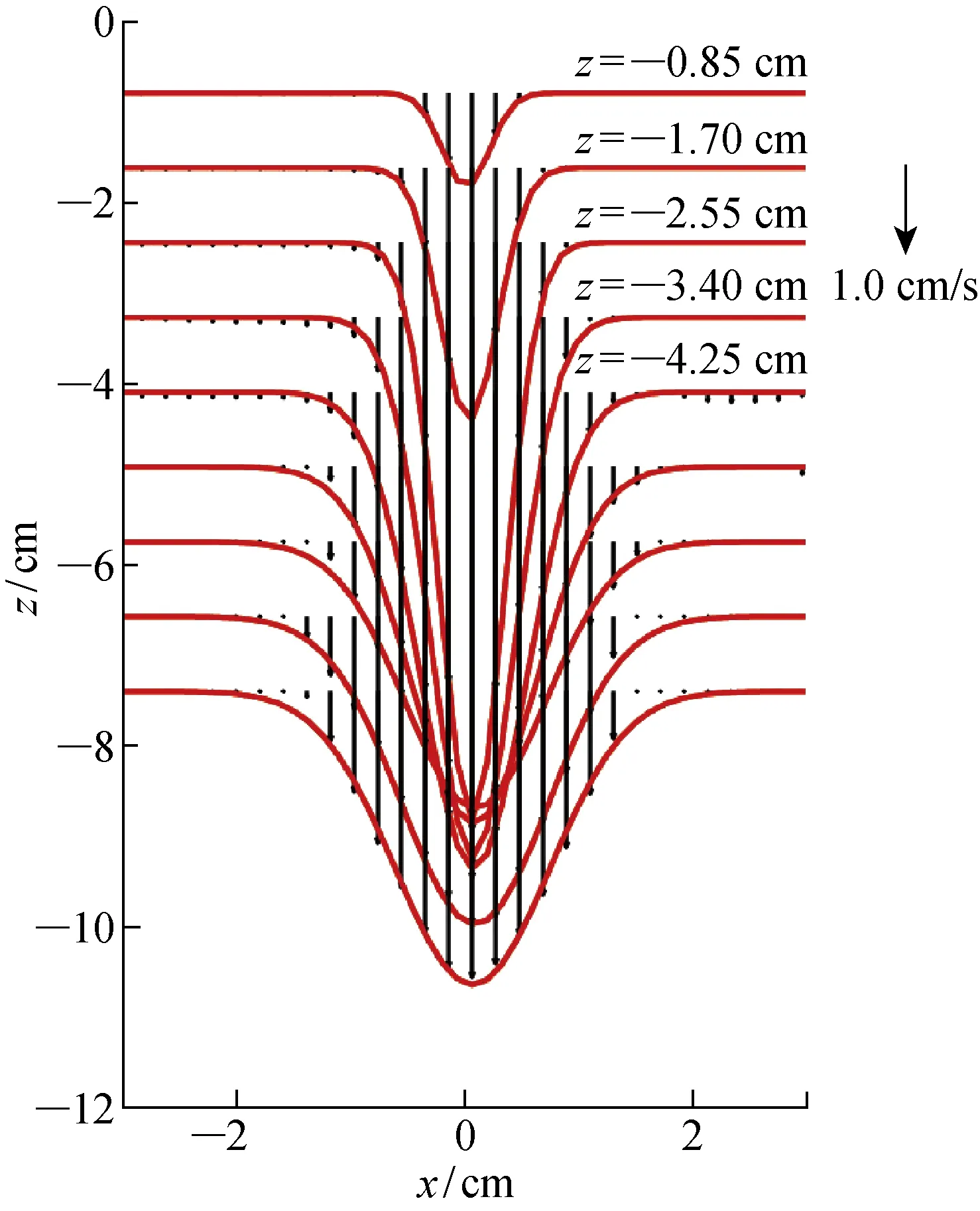
图3 垂向时均速度分量的高斯曲线拟合(工况10)Fig.3 Gaussian fitting of mean vertical velocity (Case 10)

表2 羽干各层垂向时均速度分量的高斯曲线拟合(工况10)

Tab.2 Results of Gaussian fitting for mean vertical velocity component at each level (Case 10)

z/cmWm/(cm·s-1)xm/mmb/mm拟合残差-0.85-1.460.504.356.20×10-7-1.70-3.690.924.752.69×10-6-2.55-5.841.015.563.27×10-6-3.40-5.781.116.652.17×10-6-4.25-5.381.207.956.83×10-6-5.10-4.771.269.042.17×10-5-5.95-3.961.369.905.38×10-5-6.80-3.931.4210.24.98×10-5-7.65-3.621.2010.36.98×10-5-8.50-2.871.6010.26.89×10-5-9.35-1.401.707.561.28×10-5

图4 所有工况的αe随标准化穿透深度分布Fig.4 αe for all cases versus normalized penetration

2.2 输移质量

将式(5)代入式(9)，并将直角坐标系转化为相应的圆柱坐标系，可得：

(10)

变形可得：

(11)

本文实验中喷口出流盐水密度与层结环境的盐水密度差异均在3%以内，可认为满足Boussinesq假设，即密度变化对羽流发展的影响可忽略[5].假定在同一深度的羽流内部密度恒定且为常数，因此式(11)中的密度ρ(z)只是z的函数，与r无关.对式(11)进行积分求解，

(12)

代入并整理可得：

M(z)=πρWmb2

(13)

式(13)与文献[2]中气体羽流水平截面的质量流量表达式相同，垂向质量通量与最大垂向速度分量和羽流半径这两个参数密切相关.采用式(13)得到标准化垂向质量通量随标准化穿透深度分布，如图5所示.羽流垂向质量通量从喷口处开始迅速增加，到喷口附近z≈-0.1Zmax处增速变缓，再到z≈-0.65Zmax处达到最大值，此后逐渐减小直到接近于0.当z=-0.65Zmax，该处属于中性浮力层，这说明在中性浮力层以上，羽流由于卷吸作用不断从周围环境吸收质量；在中性浮力层及以下，携带大量物质的羽流向四周扩散，同时将自身携带和环境吸收的物质输运到更远处.

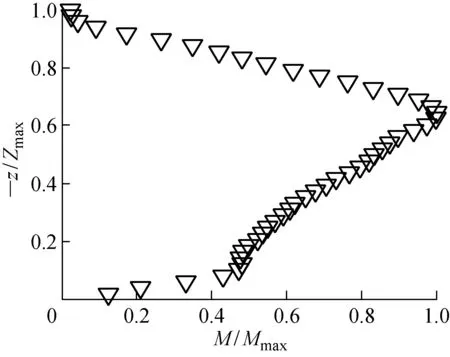
图5 所有工况M/Mmax随标准化穿透距离分布Fig.5 M/Mmax versus normalized penetration

根据π定理，对最大质量通量Mmax进行量纲分析，得到其函数表达式：

Mmax=CMρaB3/4N-5/4

(14)

式中：CM为待定常数，可由实验确定；所有工况的最大垂向质量通量相关参数见表3.对所得数据进行线性相关分析，结果如图6所示，矩形符号表示原始数据，实线表示拟合直线.

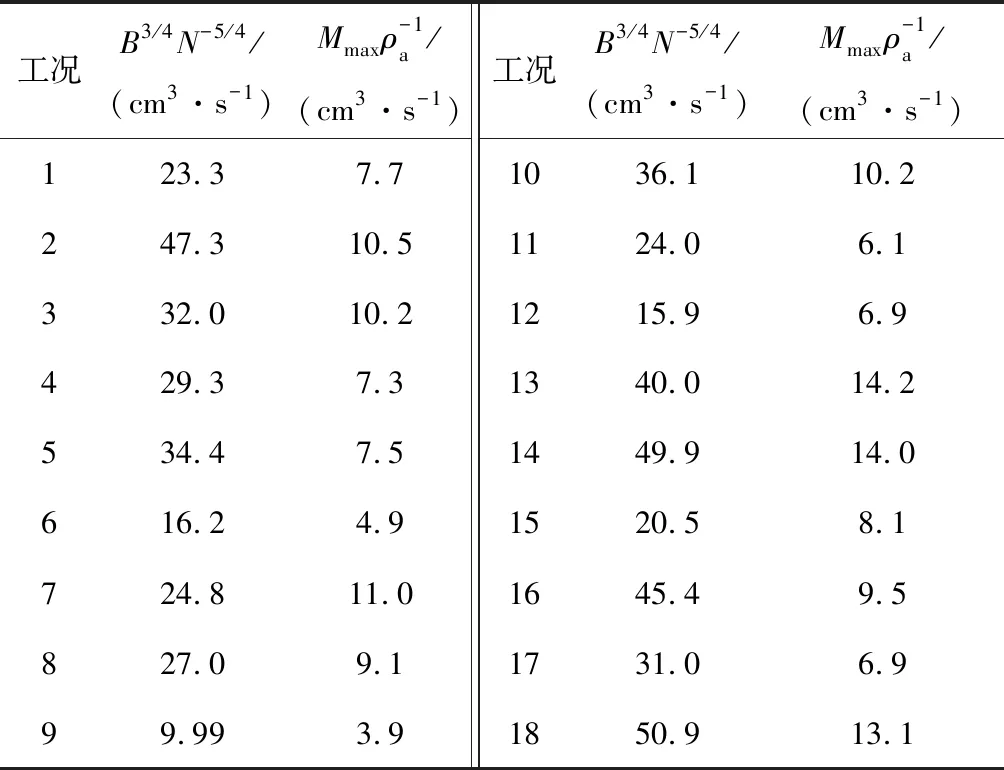
表3 Mmax线性相关分析的相关参数Tab.3 Parameters with linear correlation for Mmax

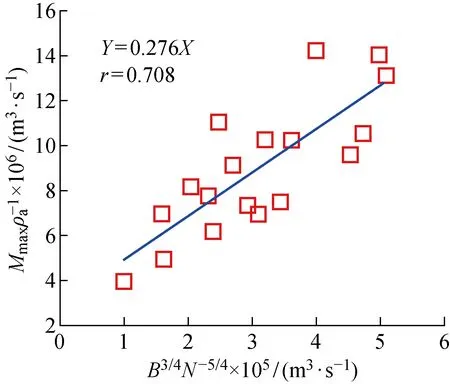
图6 Mmax线性相关分析结果Fig.6 Linear correlation for Mmax

通过最小二乘法计算得到Pearson相关系数，评估线性相关程度，用r表示，r值越大表示相关性越强.所有工况数据拟合得到r=0.708，待定常数CM=0.276.通过假设检验，计算P值为 1.01×10-3(P<0.01，样本量n=18)，这表明Mmax/ρa与B3/4N-5/4有显著的线性相关性.线性层结环境中的羽流Mmax由B、N和ρa共同决定：

Mmax=0.276ρaB3/4N-5/4

(15)

结合羽流卷吸系数分布、质量通量分布及羽流的发展演化形态[12]可知：从喷口喷出的浮力羽流在羽干处卷吸入周围环境流体后沿射流方向被输移到更远处；在羽帽区，羽流与吸入的环境流体发生混合后，最终在中性浮力层被输移到周围，这是浮力羽流的物质输移过程.

2.3 误差分析

本文层结环境中的浮力羽流是典型的变密度流动，折射率会随着流体局部密度的变化而改变.折射率的非定常会引起图像中示踪粒子的模糊，导致PIV测量误差.折射率变化引起的速度脉动现象被称为伪湍动，有必要评估其大小.

沿着中心线方向，在喷口下方2 cm处垂直固定一根直径为2 mm的黑色细杆，并在杆表面标出7个白点，如图7所示.在相同的实验设置基础上，不在层结盐水及射流盐水中添加PIV示踪粒子，并重复实验工况10，得到层结环境中浮力羽流中心线7个固定点的瞬时速度时间序列.其中，位于羽干中部点B的瞬时速度随时间波动最为剧烈，其时间序列如图8所示， 时均速度分量为UB=1.1×10-3m/s,WB=-2.0×10-3m/s.工况10的相同位置的垂向时均速度分量为W=6.2×10-2m/s，即由式(13)计算羽流最大输移质量，最大误差约3%.因此，伪湍动对于羽流的真实时均速度场影响有限，对于浮力羽流最大输移质量的影响可忽略.

图7 初始时刻通过固定点评估伪湍动的PIV图Fig.7 The image of fixed particles for the initial moment collected by PIV to assess pseudo turbulence

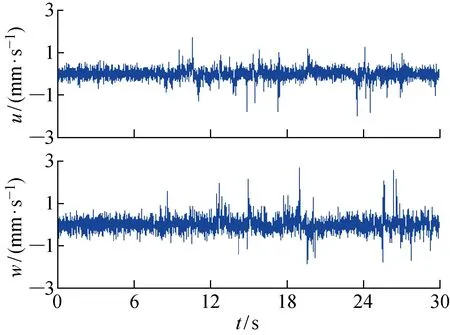
图8 折射率变化引起的羽流流场中固定点B的瞬时流速时间序列Fig.8 Measured time series of velocity components of fixed Particle B due to variations of refractive index

3 结语

在线性层结盐水中开展浮力羽流实验，通过PIV技术获得流场数据，分析其卷吸及质量输移过程，提出浮力羽流最大输移质量计算公式.

(1) 羽流位于相同高度处的垂向速度分量符合高斯分布.从喷口原点至z≈-0.3Zmax范围内，αe逐渐增加；在z≈(-0.3～-0.5)Zmax时，αe在 0.11 附近波动；在z≈(-0.5～-0.7)Zmax时，αe逐渐减小至0；在z≈(-0.7～-1)Zmax时，αe为负值.

(2) 从喷口喷出的浮力羽流在羽干处卷吸入周围环境流体后沿射流方向被输移到更远处，在 -0.65Zmax处羽流垂向质量通量达到最大值；在羽帽区，羽流与吸入的环境流体发生混合后，在中性浮力层被输移到周围，垂向质量通量减小至0.Mmax由浮力通量、浮力频率和与喷口处于相同高度的周围环境密度共同决定.

(3) 折射率变化引起的伪湍动对于羽流真实速度场的影响可忽略，其导致的浮力羽流最大输移质量计算误差约为3%.

本文实验在静止恒温的盐水环境中进行，有待进一步开展考虑侧向流、温度变化等环境条件下的羽流实验.本文得到的最大输移质量计算公式及相关结论为系统研究羽流演化过程中产生的物质混合与输移提供了理论依据.