隧道火灾羽流质量流量计算公式的研究

付 召 王子云

（四川大学建筑与环境学院 成都 610065）

0 引言

隧道给人们的出行带来了巨大的便利，但同时也给人们提出了诸多的安全挑战。其中隧道火灾给人们带来的危害更是不容忽视[1,2]。隧道空间结构复杂，空间狭小，纵深较长，出入口少，封闭性强，一旦发生火灾，烟雾难以排出。据统计，火灾中大部分人员是因吸入烟气等有毒气体窒息而亡[3]。故如能将隧道烟气及时有效排除，则能大大减少火灾人员伤亡。隧道排烟一般分为纵向排烟与横向排烟，传统纵向排烟的缺陷在于烟气沿隧道扩散，若遇隧道堵塞工况，高温烟气会对隧道堵塞人员造成严重伤害。而横向排烟系统虽然成本较高，但由于不存在纵向排烟系统的诸多缺陷，其应用正日益扩大。对于前者，国内外学者已进行了深入研究，在工程应用上已较为成熟，而对于横向排烟系统的研究还相对较少。

横向排烟系统设计的首要任务是确定排烟量，而排烟量与烟气层分界面处羽流质量流量密切相关。NFPA92B轴对称羽流模型是目前隧道火灾横向排烟设计工程中广泛采用的模型，但实际隧道火灾工况与该模型的假设条件有诸多不符，这必将影响该模型公式的计算精度。

本文利用FDS火灾动力学模拟软件对隧道火灾工况进行模拟，将不同工况下羽流质量流量模拟值与NFPA92B模型计算值，CIBSE模型计算值，以及本文提出的CIBSE修正模型计算值进行对比分析。

1 两种羽流模型概述

1.1 NFPA92B轴对称羽流模型概述

式（1）～（3）为NFPA92B轴对称羽流模型质量流量计算公式[4]。

式中，Z1为限制高度，m；Z为火焰底部至烟气层交界面距离，m；Qc为火源热释放速率的对流部分，kW，一般取Qc=0.7Q，Q为火源热释放速率；mp为高度Z处羽流质量流量，kg/s。

该模型是在Heskestad经验模型基础上加以修正提出的，而Heskestad经验模型仅对平均火焰高度以上区域的描述较为准确；同时，仅有实验证明在小面积火源工况下（2）式与实验结果符合得较好，而隧道高度较低，火灾释热率较高，一般处于Z1高度以下，须采用（3）式计算，但到目前为止，尚无关于（3）式的验证实验数据。

1.2 CIBSE线性火源羽流模型概述

式（4）～（6）为CIBSE线性火源羽流模型质量流量计算公式[5]。

式中，ds为火源长边长度，m。

根据CIBSE的描述，矩形火源长边超过短边三倍以上，可将其视为线性火源，其不同高度处羽流质量流量可按（4）～（6）式计算得到。其中（5）式中的系数是基于Lee与Emmons[6]理论提出的。

2 模拟值与两种模型计算值对比分析

2.1 数值模拟模型建立及网格划分

FDS是美国国家技术标准局（NIST）开发的权威火灾模拟软件[7]，其采用的计算核心为大涡模拟，而合理的网格划分是准确模拟的前提，结合相关资料[8]，设置网格尺寸为0.075D*。其中：

式中，D*为火源特征直径，Q为火灾总释热率，kW。

结合目前隧道建设的断面类型，选取截面为9m×4.5m（宽×高），18m×4.5m与 9m×7m，18m×7m的四种常见隧道尺寸。由于在不影响羽流发展情况下，隧道宽度对羽流质量流量并无影响，故本次模拟仅考虑宽度为9m的隧道模型，具体隧道模型尺寸设置为40m×9m×4.5m（长×宽×高）与40m×9m×7m两种。

结合PIARC，RABT，CETU，NFPA502等机构建议数据，火灾工况的设计如表1所示，火源设置在隧道底部中央位置。

表1 隧道火灾工况设计Table 1 The design of fire conditions

由于工程上一般将烟气层控制在0.8H以上，故对于H=4.5m与H=7m两种隧道模型分别监测0.8H高度平面，即3.6m与5.6m高度平面处羽流质量流量。

2.2 模拟值与模型计算值对比分析

在上述隧道火灾工况下，模拟值分别与NFPA92B轴对称羽流模型计算值，CIBSE线性火源羽流模型计算值的对比情况如图1～图2所示。

图1 模拟值与NFPA92B轴对称羽流模型计算值对比Fig.1 The comparison of value of simulationand the value calculated by NFPA92B

图2 模拟值与CIBSE矩形火源羽流模型计算值对比Fig.2 The comparison of value of simulation and the value calculated by CIBSE

分析上图可知，在常见隧道火灾工况下，NFPA92B轴对称羽流模型计算值普遍较模拟值偏低。这是由于由式（3）有该经验关系式并未体现火灾面积对羽流质量流量的影响，故在火源释热率较低时，计算值较模拟值偏小，这点在大面积火源火灾工况下体现较为明显，当火灾释热率增加到一定程度，面积对羽流质量流量的影响减弱，故计算值超过了模拟值；CIBSE矩形火源羽流模型计算值较模拟值偏大较多，这是由于由式（5）有该经验关系式在降低火源释热率对羽流质量流量影响的同时考虑了火源面积的影响，但将长边对羽流质量流量的影响考虑过大，这点在火源释热率较大时体现尤为明显。

3 CIBSE修正公式的提出及验证

车辆尺寸一般长边为短边的2倍以上，一般宽度在2.5m左右，短边长度对羽流同样具有一定影响，故将式（4），（5）中的长边长度ds用矩形火源当量直径Di替代，提出如下式（7）～（9）CIBSE羽流修正模型。

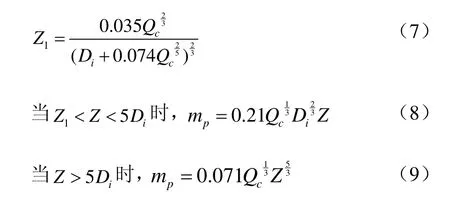
式中，Di为火源当量直径，m。其中a为火源长度，m；b为火源宽度，m。

其中，式（6）与式（9）完全相同，在隧道火灾工况下基本不采用。

其在Z=0.8H高度处羽流质量流量计算值与模拟值对比如图3所示。

图3 模拟值与CIBSE矩形火源羽流修正模型计算值对比Fig.3 The comparison of value of simulation and the value calculated by amendment model of CIBSE

由图1～图3比较可知，CIBSE矩形火源羽流修正模型计算值与模拟值最为接近，这是由于将CIBSE矩形火源羽流模型中的火源长边长度ds用当量直径Di替代，其目的是综合考虑长边，短边对羽流质量流量的影响，也即在考虑面积对羽流质量流量影响的同时减小了长边对羽流质量流量的影响。

4 结论

预测烟气分界面处羽流质量流量是隧道横向排烟系统设计的基础。目前常见的火灾羽流模型均是基于实验拟合的经验公式，由于实验条件不同，各自有着不同的适用范围，仅能在一定范围内确保其精度。在目前隧道火灾横向排烟设计中，NFPA92B轴对称羽流模型的应用较多，CIBSE矩形火源羽流模型的应用则较少。

模拟结果表明，在常见火灾工况下，CIBSE模型计算值与模拟值误差较大，工程中不宜采用；在7m高隧道模型火灾工况下，NFPA92B模型计算值与模拟值较为接近，在4.5m高隧道模型火灾工况下，计算值较模拟值偏低较多，但在超大型火灾释热率情况下（>100MW），计算值均较模拟值偏大过多，故该模型仅能满足部分火灾工况精度；而本文提出的CIBSE矩形火源羽流修正模型计算值与模拟值较为接近，并且在多种常见火灾工况下与模拟值符合很好，具有良好的工程应用前景。