远程多光束激光相干场成像拍频误差校正研究∗

张羽 罗秀娟 刘辉 陈明徕 兰富洋 贾辉 曹蓓

(中国科学院西安光学精密机械研究所,西安 710119)

1 引 言

多光束激光相干场成像已成为地基对空目标高分辨率观测的重要手段,它结合主动照明的优势,利用各同源光束间的干涉信息获取远距离目标的空间分布特征,通过对目标回波信号的接收与解调重构目标图像.尽管多光束构成干涉信息的方式随成像原理不同而各有差异,如基于多组干涉条纹的傅里叶望远技术[1−5]和基于散斑场干涉的剪切光束干涉望远技术[6−9]等,但其中都涉及到多光束频率调制这一关键技术.尤其是基于多光束的傅里叶望远术,频率调制的精度直接决定着成像质量.该技术采用声光调制对各个光束加载不同的微小频移得到不同的外差干涉拍频量,用以携带目标不同空间频率的信息.

真实成像系统中存在着更为复杂的频率偏移因素,如大气湍流扰动、高功率声光移频和光放大器件等.近些年国内外一些学者主要针对成像稳定性以及频率调制特性进行了专项研究,如西班牙Astro fi sica研究所的Montilla团队[10]进行了阵列波前特性及相应控制算法的研究.美国Florida Atlantic University的William团队[11]开展了水平湍流路径中采用时域平均方法使傅里叶望远清晰成像的研究,Andes大学的Gares团队[12]采用了层析法对空间目标进行了3D成像,Stephen团队[13]在原有傅里叶望远镜的基础上研制了4 m阵列发射系统,针对空间目标展开成像实验.中国科学院光电研究院的孔新新对傅里叶望远镜中频率误差对成像质量的影响进行了分析[14,15];中国科学院西安光学精密机械研究所的曹蓓等[16]以及国防科技大学的陈卫等[17]利用全相位法修正了由于激光频率稳定性差而造成的频率偏差等.

在分析频差对成像影响的基础上,仍需要进一步提出有效抑制频漂的方法.尽管全相位法抑制了激光源的频率抖动,但对于高功率多光束干涉成像而言,尚不能分别对各光束进行独立校正.考虑到设计成本,系统会采用先分束、再放大的输出方式.每束光在声光调制、传输路径上也具有独立性,故需要研究一种针对各个光束独立校正的方法.本文以傅里叶望远技术为基础,光束拍频量作为研究对象,提出并比较了 “动态解调”和“置信区间解调”两种拍频校正方法,理论分析了“动态解调”可行性和适用范围,实验验证了“置信区间解调”对重构过程的优化,在系统数据处理端对各组傅里叶分量的拍频漂移进行了修正.

2 傅里叶望远技术及拍频漂移分析

多光束相干场望远技术中最为典型的即为傅里叶望远技术,其成像原理如图1所示,阵列中各光束根据Golumb ruler设定不同的量频移[18],输出后进行外差干涉,各基线位置处的光束组在目标表面形成了不同空间频率和方向的干涉条纹来提取目标空间信息,在信号被接收后,根据每组拍频信号所携带的信息将目标图像解调重构.

图1 傅里叶望远技术成像系统示意Fig.1.Concept of Fourier telescopy.

为了保证基本的光束相位闭合运算,本文以T型阵列三光束成像系统进行分析.假设激光束场强用指数信号表示为Ei=exp(iωit).若三束同源激光信号表示为E1,E2,E3.它们在目标表面干涉条纹的能量分布为

式中,k1=k0Δx1/R,k0=2π/λ为波数;Δx1,Δx2,Δx3分别为发射基线上三个发射孔径两两之间的距离;R是目标的观测距离.ϕ1,ϕ2,ϕ3是光束的初始相位;其中,c.c=(exp(i(ω1−ω2)t)+exp(i(ω2−ω3)t)+exp(i(ω3−ω1)t))∗,此时三个拍频量已经形成,光束照射目标后到达探测器阵列,回波信号的三组傅里叶变换表示为

即三光束外差干涉构成的拍频量,其中Mi,j为在T型阵列中某两束光的干涉幅值,其中c′′=Nc.c,N为数据采样点数,O(ki−kj)为在阵列i,j两处光束干涉采集的目标空间频谱.探测器接收到的时域序列及其拍频如图2所示.

图2 目标回波信号 (a)时域信号;(b)频域拍频信号Fig.2.Returning signal from target:(a)Time domain;(b)beat signal in frequency domain.

由于射频驱动误差、功率放大噪声以及湍流扰动等因素的存在,均会使提取目标信息的拍频出现漂移,特别是系统声光调制的频率漂移.这是由于射频驱动及频率合成器件的频率稳定性,以及在信号驱动放大过程中温度稳定度对频率漂移存在影响,其声光调制过程如图3所示.

研究发现在这一过程中使得kHz级的调制频率会出现100 Hz左右的漂移,尽管漂移量相对kHz较小,但作为多光束干涉系统而言,往往会产生干涉混乱现象,例如利用图4中的目标进行频漂仿真.

图3 傅里叶望远镜光束声光调制过程Fig.3.Procedure of Acoustic-optical modulation.

图4 仿真目标Fig.4.Simulation target.

三光束拍频设定在30,60和90 kHz,给三束光同时加上频率的影响,在RMS都为1000的情况下,分别使频率的变化范围为100,200,300和400 Hz,得到的重构图像如图5(a)—(d).从图5可以看出,当三束光都加上频率抖动后,不管频率变化范围多少,在没有频率混叠的情况下,其重构出的图像质量很低,与目标图像比较,基本上完全失真.

在真实的T型发射阵列中,参与的光束不仅仅只有三束,光束间一旦独立夹杂了频漂噪声,会更加影响系统成像质量.因此,本文从两种优化解调方法入手,分析其可行性与适用性.

图5 三光束加载频差抖动后的重构图 (a)100 Hz;(b)200 Hz;(c)300 Hz;(d)400 HzFig.5. Reconstruction after applying beat frequency fl uctuation simultaneously on three beams:(a)100 Hz;(b)200 Hz;(c)300 Hz;(d)400 Hz.

3 两种优化解调方法模型分析

3.1 动态解调模型仿真分析

所谓动态解调,是将拍频量视为携带目标信息的载波,当拍频在某一范围内漂移时,所达到的位置即被认为是信号载波所在的位置,在该位置处进行频率解调,即在一定范围内解调的频率随拍频漂移量动态变化.其解调过程如图6所示.

图6 动态解调法流程图Fig.6.Procedure of dynamic demodulation.

在某一基线处,任意两光束间的拍频漂移为Δferror,其角频率漂移为Δωerror=2πΔferror,则由目标返回的时域信号如(3)式所示:

其中T为数据采样周期,I为光强,fnm为拍频.则在该基线处的频谱为

此时,需要调节采样周期T使得N(ωnm+Δωerror)T=2mπ方使得回波信号的傅里叶变换为

此时,若三个拍频的偏移量分别为Δωerror1,Δωerror2,Δω则三光束构成的频谱为

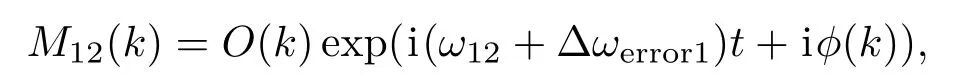
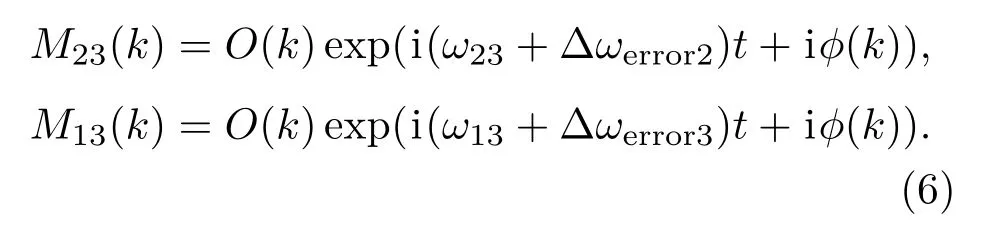
不同基线的相位闭合以及频谱迭代[19−21]时均按照已偏离的拍频进行,以90 kHz的拍频为例,当其发生200 Hz的偏移时,将信号在该处的解调频率定为90 kHz+200 Hz.随后在对应的拍频处解调.

然而在实际成像系统中,每个基线均存在着不同程度的瞬时频率漂移.这对硬件系统的响应速度是个极大的挑战.为了从原理上验证该解调方法,本部分仿真中频率变化设计为阶跃式的缓慢变化,即认为三光束在基线遍历时在低、中、高频各产生一次变化,以模拟真实环境中极端温度等因素造成的缓慢频率变化:将发射基线构成的频谱面分为低频、中频、高频三部分,T型阵列三光束干涉所构成的干涉谱分布如图7所示,红色亮点部分为划分的基线空间谱,每一部分给三光束加载随机的频率漂移(通常频率的随机漂移在100 Hz左右).

采样点数设为12000,基线遍历到10×10的成像结果与未校正的图像对比如图8所示.

通过对该方法的研究,可以看出动态解调法在一定程度上对拍频漂移有抑制作用,然而该方法更适合抑制频率漂移较为缓慢的因素,在实际成像系统中需要实时调整系统的解调频率,若频率变化较快,监测与变频程序速度无法与频率变化匹配,经常会导致图像中出现条纹状噪声,匹配不好时没有任何目标信息,因此该方法对系统解调硬件的要求较高,若硬件的采样率、响应率具有更高的性能,该方法的频漂抑制作用会显著提升.

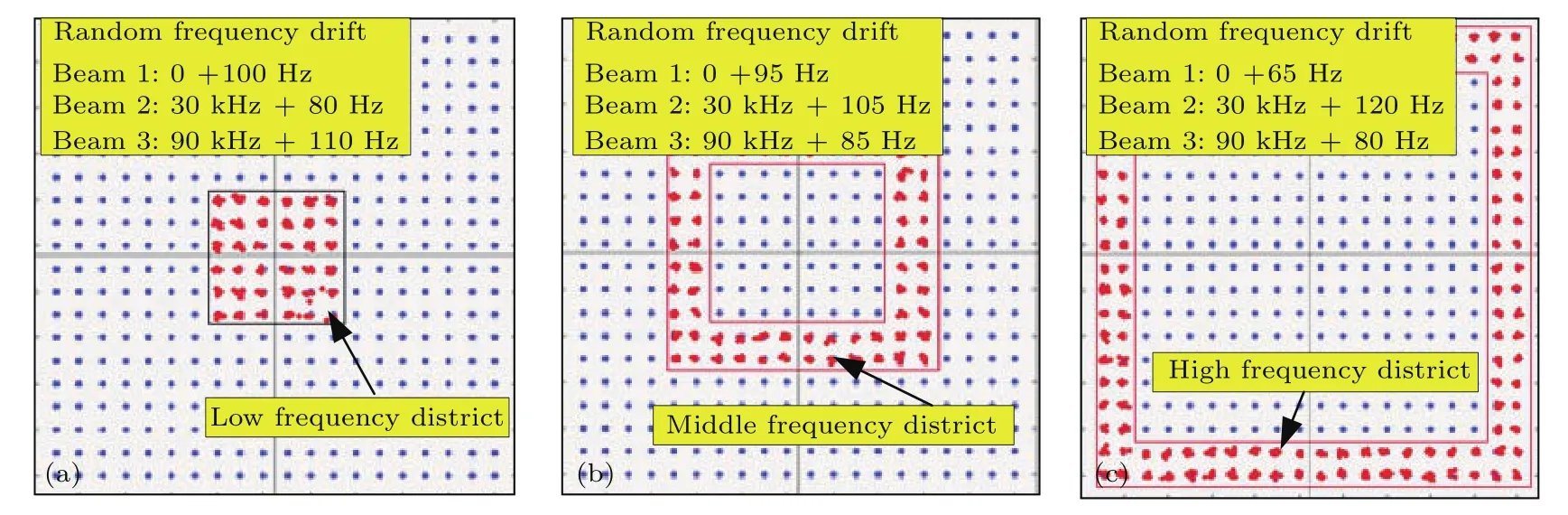
图7 在不同频谱区域引入误差 (a)低频区;(b)中频区;(c)高频区Fig.7.Random beat frequency drift induced in different spatial region:(a)Low frequency;(b)medium frequency;(c)high frequency.

图8 阵列10×10基线处的矫正效果对比 (a)传统解调方法;(b)动态解调法Fig.8.Comparison of two demodulations on transmitter array of 10×10 baseline:(a)Traditional demodulation;(b)dynamic demodulation.

3.2 置信区间叠加解调模型分析

上节在理论上仿真了动态解调法的重构过程,其时效性上仍有待于进一步提升.本节分析的置信区间叠加法是将拍频漂移范围取一个有用信号区间,认为在这个区间内的信号均为有用信号,将此区间内所有信号能量均叠加在设定频率处,在原设定频率点解调.此解调方法的流程如图9所示.

由成像原理可知,傅里叶望远技术的信号接收和频谱迭代主要依靠回波信号的能量迭代来完成,因此当拍频信号发生漂移或者展宽时可将一定范围内的漂移信号能量进行加权,之后在预定拍频处解调来达到增强信号的效果.以T型发射阵列中两光束干涉照射目标为例,

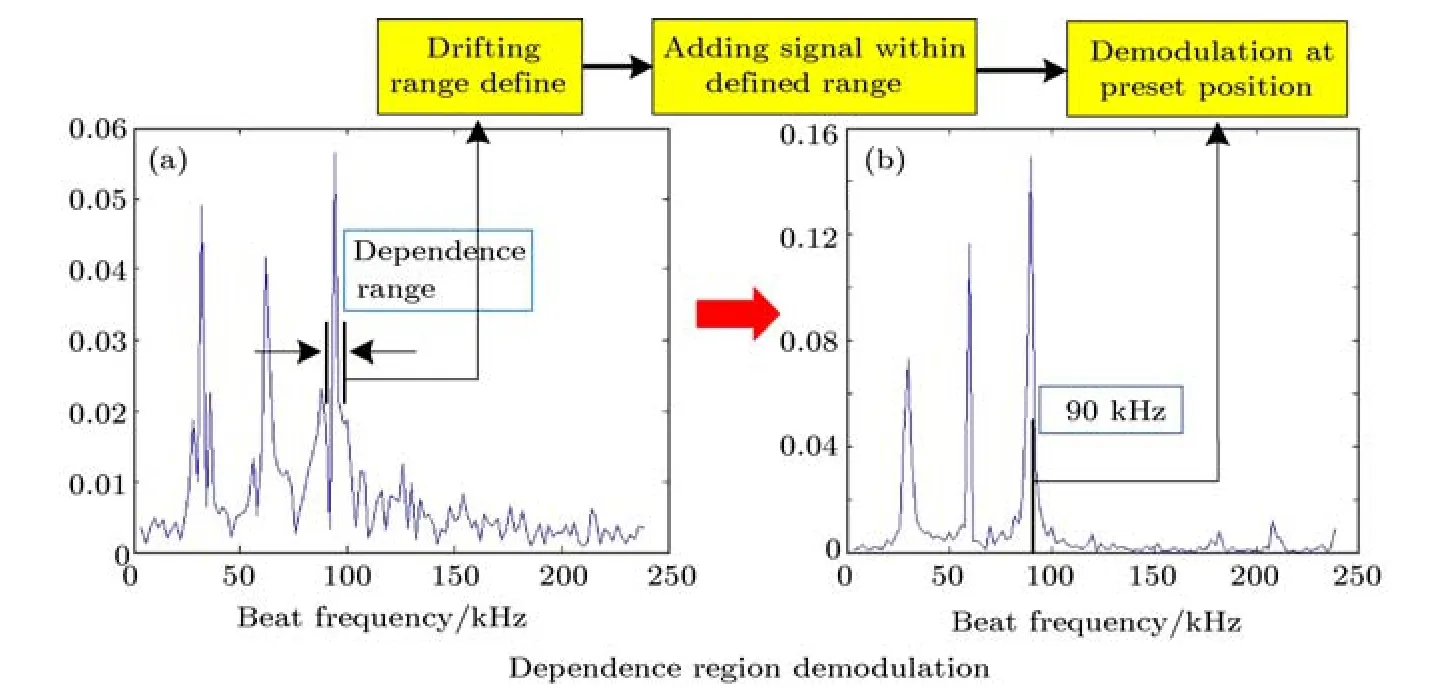
图9 频率漂移“置信区间叠加法”流程图Fig.9.Procedure of dependence range demodulation.

(7)式描述了两光束干涉并照射目标时回波信号的组成,其中O(x,y)为目标表面形态空间分布,E为两光束的复振幅,ω1和ωerr1分别为第一束光的调制频率和频率漂移,同样ω2和ωerr2分别为第二束光的频率和漂移量,c.c为复指数项的共轭.由数学表达式可知经过积化和差运算得到

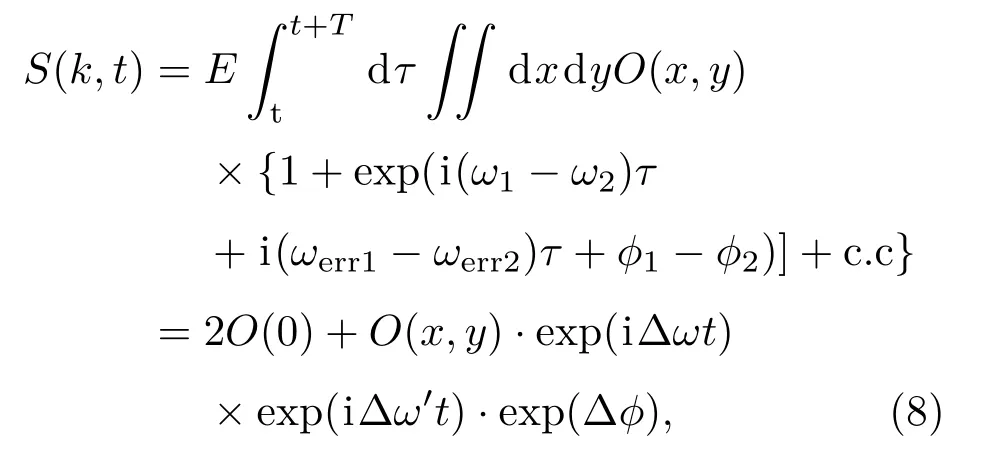
其中Δω为两光束的频率差即拍频量,而Δω′为拍频漂移量.此时回波信号的傅里叶形式为

即M(k)=Nc′O(k)exp[iΔωt+iΔω′t+iΔϕ],其中N为采样点数,c′=cE2Tsin(ΔωT/2).

考虑到傅里叶相干场成像是能量迭代运算,回波信号相位无关.当拍频漂移范围在(−Δω′,Δω′)之间,出现m个漂移位置时,将这一区间内m个拍频的能量按照(10)式进行加权,得到加权后的拍频模值同样体现了被测目标的模值,

此时通过积分叠加的新频谱信号依然参与各基线处的相位闭合与频谱迭代运算,进而获得目标的频谱函数O(k),最终通过傅里叶反变化得到目标的空间分布.下面通过实验验证该模型的可行性.

图10为验证置信区间解调法的成像实验装置,采用532 nm激光器,光束经分光镜后分为三束同源光,同时被声光调制器AOM(1—3)调制,光束布拉格一级衍射光通过扩束准直装置后进行外差干涉,得到50,100,150 kHz的“拍频”光信号,CCD与计算机1负责标定三光束的基线遍历位置,计算机2利用NI-PCI-6115采集卡对光电倍增管接收的光信号进行I/O转换,同时,拍频信号的随机漂移通过计算机2中的NI-PCI-6509控制频率合成器(acoustic-optic frequency shifter)来实现.设定置信区间为[−100—100 Hz].基于labview的数据采集程序中,置信区间设置如图11所示.

图10 置信区间解调实验装置图Fig.10.Experimental setup of dependence range demodulation.

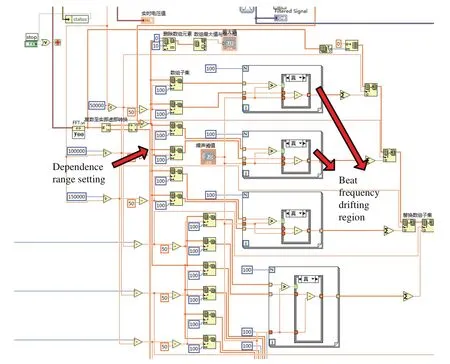
图11 Labview实现置信区间设置Fig.11.Setup of dependence range in labview.

图12 实验目标照片Fig.12.Photograph of experimental target.

图13 不同置信区间设置的重构效果 (a)传统方法重构图;(b)置信区间100 Hz;(c)置信区间200 HzFig.13.Image reconstruction of different dependence range setup:(a)Traditional reconstruction;(b)100 Hz dependence range;(c)200 Hz dependence range.

此时,数据的采样率固定为4 MHz,采样点数为12000,实验用透射式目标的制作是利用硫酸纸打印而成,以保证回波信号的均匀漫反射.实验目标照片如图12所示.

设定三个拍频漂移范围为100 Hz,在置信区间为100 Hz和200 Hz,基线遍历到10×10个点时的重构图像如图13所示.

从图像重构结果可以看出,在一定的置信区间范围内有效地抑制了拍频漂移对成像质量的影响,但需要注意的是置信区间的设置应与拍频漂移的范围相匹配,特别是当更多光束同时参与干涉,各拍频相距非常近时,置信区间不宜取值过大,以免影响图像的正确重构.

4 置信区间解调法在湍流环境的成像应用

为了验证置信区间解调法在实际湍流环境中的成像质量,开展了200 m室外实验和1.2 km湍流环境实验,实验现场如图14所示.

图14 湍流环境中外场成像实验 (a)200 m路径;(b)1.2 km路径Fig.14.Field experiments in turbulence:(a)200 m range;(b)1.2 km range.

在200 m实验中同样采用图12中的目标,利用传统解调方法和置信区间解调方法对比如图15所示.

同时,为了验证目标重构多样性,在200 m对以下四种目标(图16)进行置信区间叠加重构,得到的结果如图17所示.

水平路径1.2 km的实验中,通过对温度、大气相干长度等参数的测量与计算,认为在该地区(海拔400 m)时的大气湍流强度等效于垂直距离30 km的湍流强度,该强度基本覆盖了大气平流层的主要湍流范围,实验采用25 mm目标,放置于发射阵列1.2 km处,实验现场如图14(b)所示,原始目标和重构图像如图18所示,目标细节尺寸为5 mm,由此可计算出成像的角分辨率达到4µrad.

图15 两种重构方法200 m实验对比 (a)传统解调方法;(b)置信区间解调方法Fig.15.Comparison of two demodulations in 200 m field:(a)Traditional demodulation;(b)dependence range demodulation.

图16 200 m室外实验透射式目标尺寸(上)与实物照片(下)Fig.16.Different target calibrations used in 200 m field(up)and the photos(down).

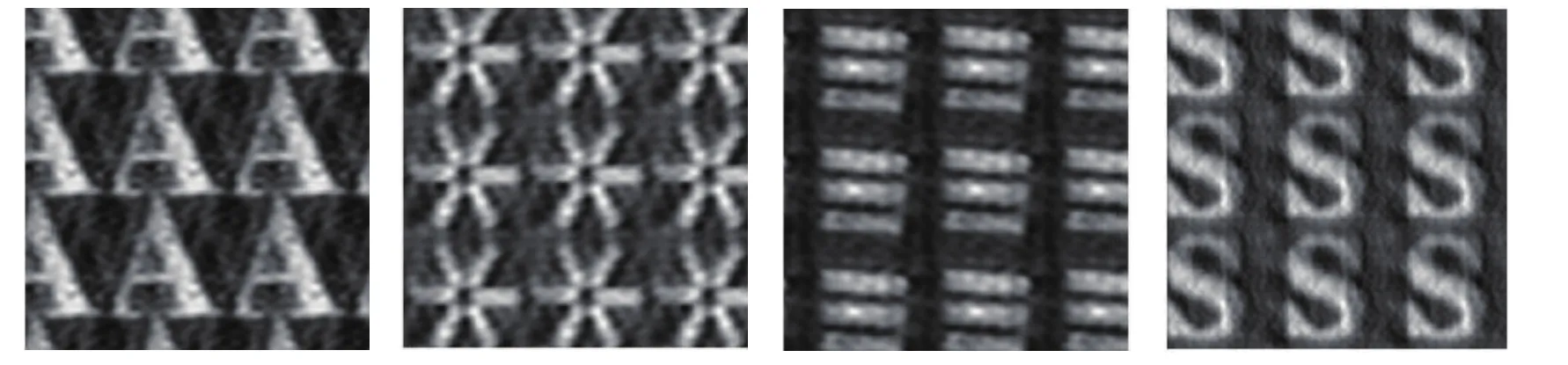
图17 200 m置信区间解调法对四种目标重构Fig.17.Image reconstruction in 200 m field by dependence range demodulation.

图18 1.2 km置信区间解调法对目标重构Fig.18.Image reconstruction in 1.2 km field by dependence range demodulation.

5 结 论

本文以三光束傅里叶激光干涉望远技术,分析了多光束激光相干场成像中的拍频漂移校正方法,提出了动态解调和置信区间解调法,仿真分析和实验表明动态解调法可在系统拍频变化缓慢时起到优化重构作用,频率变化较快时其效果取决于更高的系统硬件性能.置信区间解调并无频率变化速度的限制,在合适的置信区间内可有效提升图像重构质量.在后续的研究中,需要进一步对其在中强湍流中的成像稳定性进行研究.

[1]Holmes R B,Ma S,Bhowmik A,Greninger C 1996J.Opt.Soc.Am.A13 351

[2]Lu C M,Gao X,Tang J,Wang J J 2012Proc.SPIE8551 855110

[3]Zhang W X,Xiang L B,Kong X X,Li Y,Wu Z,Zhou Z S 2013Acta Phys.Sin.62 164203(in Chinese)[张文喜,相里斌,孔新新,李扬,伍州,周志盛2013物理学报62 164203]

[4]Zhang Y,Luo X J,Cao B,Chen M L,Liu H,Xia A L,Lan F Y 2016Acta Phys.Sin.65 114201(in Chinese)[张羽,罗秀娟,曹蓓,陈明徕,刘辉,夏爱利,兰富洋2016物理学报65 114201]

[5]Dong L,Wang B,Liu X Y 2010Chin.J.Opt.Appl.Opt.3 440(in Chinese)[董磊,王斌,刘欣悦 2010中国光学与应用光学3 440]

[6]Hutchin R A 2012US Patent0292481 A1

[7]Chen M L,Luo X J,Zhang Y,Lan F Y,Liu H,Cao B,Xia A L 2017Acta Phys.Sin.66 024203(in Chinese)[陈明徕,罗秀娟,张羽,兰富洋,刘辉,曹蓓,夏爱利2017物理学报66 024203]

[8]Lu C M,Chen M L,Luo X J,Zhang Y,Liu H,Lan F Y,Cao B 2017Acta Phys.Sin.66 114201(in Chinese)[陆长明,陈明徕,罗秀娟,张羽,刘辉,兰富洋,曹蓓2017物理学报66 114201]

[9]Lan F Y,Luo X J,Chen M L,Zhang Y,Liu H 2017Acta Phys.Sin.66 204202(in Chinese)[兰富洋,罗秀娟,陈明徕,张羽,刘辉2017物理学报66 204202]

[10]Montilla I,Bechet C,Louarn L,Reyes M 2010J.Opt.Soc.Am.27 A9

[11]William T 2012Appl.Opt.51 A11

[12]Daissy H,Garces,William T 2010Digital Holography and Three-Dimensional Imaging(Miami)DTuB8

[13]Stephen T,Ridgway,Kenneth H 2010Proc.SPIE7735 77356Z-1

[14]Kong X X,Huang M,Zhang W X 2012Acta Opt.Sin.32 1211001(in Chinese)[孔新新,黄旻,张文喜2012光学学报32 1211001]

[15]Kong X X,Huang M,Zhang W X,Wu Z,Li Y,Zhou Z S 2013Laser Optoelectron.Prog.50 011102(in Chinese)[孔新新,黄旻,张文喜,伍洲,李扬,周志盛 2013激光与光电子学进展50 011102]

[16]Cao B,Luo X J,Chen M L,Zhang Y 2015Acta Phys.Sin.64 124205(in Chinese)[曹蓓,罗秀娟,陈明徕,张羽2015物理学报64 124205]

[17]Chen W,Li Q,Wang Y G 2010Acta Opt.Sin.30 3441(in Chinese)[陈卫,黎全,王雁桂 2010光学学报30 3441]

[18]Holmes R B,Brinkley T 1996Proc.SPIE3815 11

[19]Cuellar E L,Cooper J,Mathis J,Fairchild P 2008Proc.SPIE7094 70940G

[20]Matwyschuk A 2017Appl.Opt.56 7766

[21]Mansmann R,Thomson K,Smallwood G,Dreier T,Schulz C 2017Opt.Express25 2413