稀薄里德伯原子气体中的两体纠缠∗
张秦榕 王彬彬 张孟龙 严冬2)†
1)(长春大学理学院,材料设计与量子模拟实验室,长春 130022)
2)(东北师范大学量子科学中心,长春 130117)
1 引 言
随着激光冷却和原子俘获技术的成熟进步,在20世纪末就引起广泛兴趣的里德伯原子研究再次复苏,截至目前已经在实验研究和理论预言中取得了很大进步.里德伯原子指的是最外层电子被激发到主量子数n≫1的高激发态原子,这类原子半径和电偶极矩大,寿命长,具有其他中性原子没有的特性[1].里德伯原子对外界电、磁场异常敏感,利用这个特点很容易实现里德伯原子的操控.原子间长程偶极-偶极相互作用使得里德伯原子成为量子信息应用中重要的物理资源.特别是偶极-偶极作用引起的偶极阻塞效应(dipole blockade effect),在量子信息处理中占有极其重要的作用[2−6].所谓偶极阻塞效应,是指偶极相互作用引起里德伯激发的能级移动,致使一定空间内其他原子的共振光学跃迁被抑制的现象.利用这种效应,一方面可以使光子之间引起强关联效应,进而产生可靠的单光子源[7,8]和设计单光子器件[9,10],而这些在现代量子信息处理中尤为重要;另一方面还可以制备量子纠缠态,同样,量子纠缠在量子信息和量子物理中也占有核心地位.
本文研究一种特定的少体里德伯原子系统:四个二能级原子,最高能级为里德伯态,空间位置排布为正四面体.因为任意两个原子间距均相等,所以它们之间的偶极-偶极相互作用也都相等.研究这种简单且不失一般性的里德伯原子系统的性质,既允许我们抛开近似手段进行精确的数值计算,又可以在实验室中利用超冷的稀薄原子气体来验证.本文主要讨论四原子系统的原子激发与两体纠缠的关系,不但考虑光场与原子跃迁共振的偶极阻塞机制,还把不同失谐条件下的反偶极阻塞机制的性质作为研究的重点,对比研究了稳态、瞬态高阶激发和共生纠缠的关系,分析得到实现较大纠缠的参数条件和可能的原子纠缠态.
本文第二部分构建了理论模型,给出系统的哈密顿和动力学演化方程;第三部分给出了刻画相干激发和两体纠缠的度量手段,即里德伯原子激发概率和共生纠缠;第四部分进行数值结果的讨论和分析;最后给出了简要结论.
2 系统哈密顿与动力学演化方程
稀薄里德伯原子系统,实验室中可选用超冷Rb87原子气体来实现.原子样品密度为109–1010cm−3,这时原子间平均距离可达微米量级[11].因此考虑长程偶极-偶极相互作用,完全可以用少体原子模型来描述.采用如图1(a)所示的四原子系统,任意两个原子间距离相等,原子空间位置呈正四面体结构.原子为简单的二能级结构,实验上可以在大失谐条件下绝热消除中间能级实现双光子或者三光子跃迁来获得有效的二能级原子[11−14]. 如图1(b)所示,|g〉为基态,|r〉为高激发的里德伯态.当两个原子同时激发到里德伯态上时,原子间存在偶极-偶极相互作用V.在激光光场相干驱动下,系统的哈密顿为
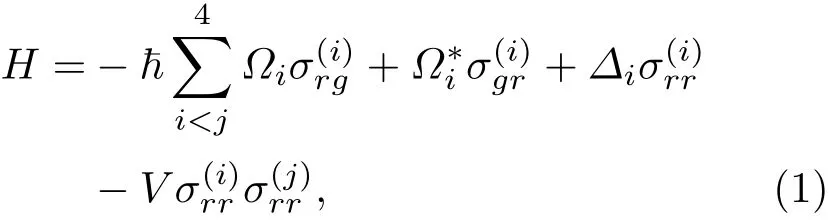
其中ħ为普朗克常数,Ωi为拉比频率,为单光子失谐,和分别为跃迁算符和投影算符.(1)式中前三项为单个原子与光场相互作用,而最后一项表示原子之间的偶极-偶极相互作用.
系统的动力学过程由原子密度矩阵ρ满足的主方程来描述:

图1(a)四原子系统中空间结构图;(b)二能级原子能级图Fig.1.(a)Schematic of spatial structure for the fouratom system;(b)the energy structure of the two-level atom.
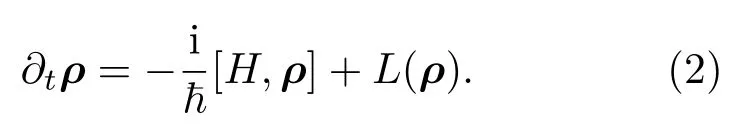
对于独立原子系综,由于原子间不存在相互作用,因此考察单原子的光学响应就能得到整个系统的光学性质.而对于里德伯原子,计及原子间偶极-偶极相互作用,原子的激发行为依赖近邻原子的存在,所以主方程所描述的问题本质上是多体问题.如果系统含有N个二能级原子,那么准确刻画系统的Hilbert空间的维数为2N.其结果就是除了两个原子的稳态问题可以精确解析求解[15,16],几个原子的情况可以通过数值精确求解以外,较一般的情况需要借助近似手段来处理,例如平均场理论[17−20]、超级原子[21−27]以及速率方程[28]等.
3 里德伯激发概率和量子纠缠的度量
在独立原子系综内原子间不存在量子关联,而里德伯原子系综则不同,激发过程中偶极-偶极相互作用使得原子间产生关联,纠缠在一起.对于四原子系统,原子激发比较复杂,需要计算几类里德伯激发概率,它们分别是单原子激发概率(平均激发概率)、双原子激发概率、三原子激发概率以及四原子激发概率,其中单原子、双原子和三原子密度矩阵分别为, 这里Tr[·]为偏迹计算.通过激发概率,可以刻画系统的激发性质,例如对于典型的偶极阻塞效应,共振的多原子激发被抑制,即高级激发概率
共生纠缠(concurrence)能够很好地度量两体纠缠,原因在于这个定义对于两个二能级原子之间的量子纠缠度量是充分必要的,其定义如下[29−31]:
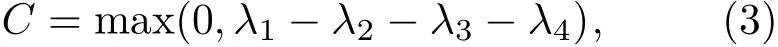

图2 稳态里德伯激发概率(a)Pr,(b)Prr,(c)Prrr和(d)Prrrr作为单光子失谐Δ/γ和偶极-偶极相互作用V/Ω的函数;图中黑色实线、蓝色折线、绿色点线以及红色点折线分别对应于Δ/V=0,1/2,1,5/4Fig.2.Steady-state Rydberg excitation probabilities(a)Pr,(b)Prr,(c)Prrr,and(d)Prrrras a function of single-photon detuning Δ/γ and dipole-dipole interaction V/Ω.The black solid,blue dashed,green dotted and dash-dotted curves correspond to Δ/V=0,1/2,1,5/4,respectively.
这里λi(i=1,2,3,4)是矩阵

本征值的平方根,它们按照降序排列,ρ(AB)是双原子的密度算符,σiy(i=1,2)是泡利矩阵,记为

共生纠缠满足0≤C≤1.C=0代表两个原子没有纠缠,即量子态是可分离的,例如两个没有相互作用的二能级原子;而C=1表示两个原子处于最大纠缠态.需要指出的是,这个定义仅仅能够判断纠缠的大小,不能直接判断纠缠态类型.
4 数值结果讨论与分析
从图2可以看出,原子各阶激发的参数空间存在明显的区域分布特征.对于共振情况,当原子间相互作用足够大时有,即原子高阶激发被抑制,系统进入典型的偶极阻塞机制.阻塞空间内只有一个原子被激发到里德伯态上,系综内所有原子形成强烈的纠缠整体,这时系统量子态具体来看,图2(a)中黑色实线标记的就是偶极阻塞参数区域,随着偶极-偶极作用的增强,单原子激发参数区域明显收紧并且在时激发概率接近饱和.而非共振情况里德伯激发行为发生明显变化.从图2(b)–(d)可以看出,围绕参数区域,系统分别产生双原子、三原子和四原子激发,这是因为一定的单光子失谐部分地补偿了由于偶极-偶极相互作用引起的能级移动,导致超过一个里德伯原子的激发行为,称之为偶极反阻塞效应[32,33].此外,高阶原子激发对低阶原子激发均有贡献.具体来讲,二、三和四个原子激发对单激发概率有贡献,三、四原子激发会增大双原子激发概率,四原子激发会提高三原子激发概率,这些信息可以从对应的参数空间获得(见图2蓝色折线、绿色点线和红色点折线).
除Δ/V=0,1/2,1,5/4四个参数区域以外,里德伯激发几乎被完全抑制.这是因为失谐或者原子间相互作用过大,有限强度的激光光场不足以将单个原子激发到里德伯态上.所以要实现里德伯激发,必须要保证足够的激光强度.

图3 稳态共生纠缠C作为单光子失谐Δ/γ和偶极-偶极相互作用V/Ω的函数,其他参数和四类曲线与图2一致Fig.3.Steady-state concurrence C as a function of single-photon detuning Δ/γ and dipole-dipole interaction V/Ω.Other parameters and four kinds of curves are the same as in Fig.2.
与原子激发行为相对应,下面讨论相同参数空间的稳态纠缠性质.从图3可以清楚地看到,量子纠缠仅存在于里德伯原子的各阶激发参数范围.在激发概率为零的地方,根本不存在量子纠缠.这意味着要想实现纠缠,至少要激发一个原子到里德伯态上才能触发偶极-偶极相互作用.此外,最大纠缠集中在偶极阻塞区域,由其量子态亦可看出,只有一个原子被激发的四体系统是一个强纠缠的量子系统.
下面详细讨论稳态纠缠、激发与原子间相互作用的关系.由图4(a)中黑色实线可以看出,在偶极阻塞条件下,当V/Ω≤2时原子间不存在纠缠,这是因为原子间偶极-偶极作用较弱,此时与独立原子类似,每个原子都有较高的概率激发,所以原子间不能很好地纠缠.而当V增大,高阶激发被逐渐抑制,其结果是平均激发概率降低,只保证一个原子激发,因此系统逐渐进入关联状态,纠缠产生并随着偶极阻塞效应的增强而增强,当里德伯原子的多激发被完全抑制,系统进入严格的偶极阻塞机制,纠缠和激发随之趋于饱和状态.而对于偶极反阻塞机制(图4(a)蓝色折线、绿色点线和红色点折线)的情况,当V/Ω≤3时,也有与偶极阻塞机制类似的性质,因此不存在纠缠.随着偶极-偶极作用逐渐增大,量子纠缠达到最大值,继续增大,量子纠缠会减弱直至消失(蓝折线也符合这个特点,只是图4(a)中没有体现出来,V/Ω>30就能看到这个特点).在偶极反阻塞效应中,尽管偶极-偶极相互作用V与失谐Δ的比例保持一致,但是由于对原子激发的作用不同,因此它们之间的具有竞争和合作关系决定着纠缠大小,当V(Δ)较小时,失谐Δ在一定程度上补偿了偶极-偶极相互作用V带来的能级移动,因此里德伯原子激发得到增强从而促进量子纠缠,当两者都很大时,失谐Δ和V都在一定程度上降低了单原子激发,而且补偿的能级移动带来的效果微不足道,因此最后原子激发被完全抑制,所以量子纠缠消失.

图4(a)稳态共生纠缠C和(b)里德伯激发概率作为偶极-偶极相互作用V/Ω的函数(黑色实线、蓝色折线、绿色点线以及红色点折线分别对应于Δ/V=0,1/2,1,5/4)Fig.4.(a)Steady-state concurrence C and(b)Rydberg excitation probabilities as a function of dipole-dipole interaction V/Ω.The black solid,blue dashed,green dotted and dash-dotted curves in(a)correspond to Δ/V=0,1/2,1,5/4,respectively.

图5(a)稳态共生纠缠C和(b)里德伯激发概率作为失谐Δ/γ的函数,其中偶极-偶极相互作用V/Ω=5Fig.5.(a)Steady-state concurrence C and(b)Rydberg excitation probabilities as a function of single-photon detuning Δ/γ with dipole-dipole interaction V/Ω =5.
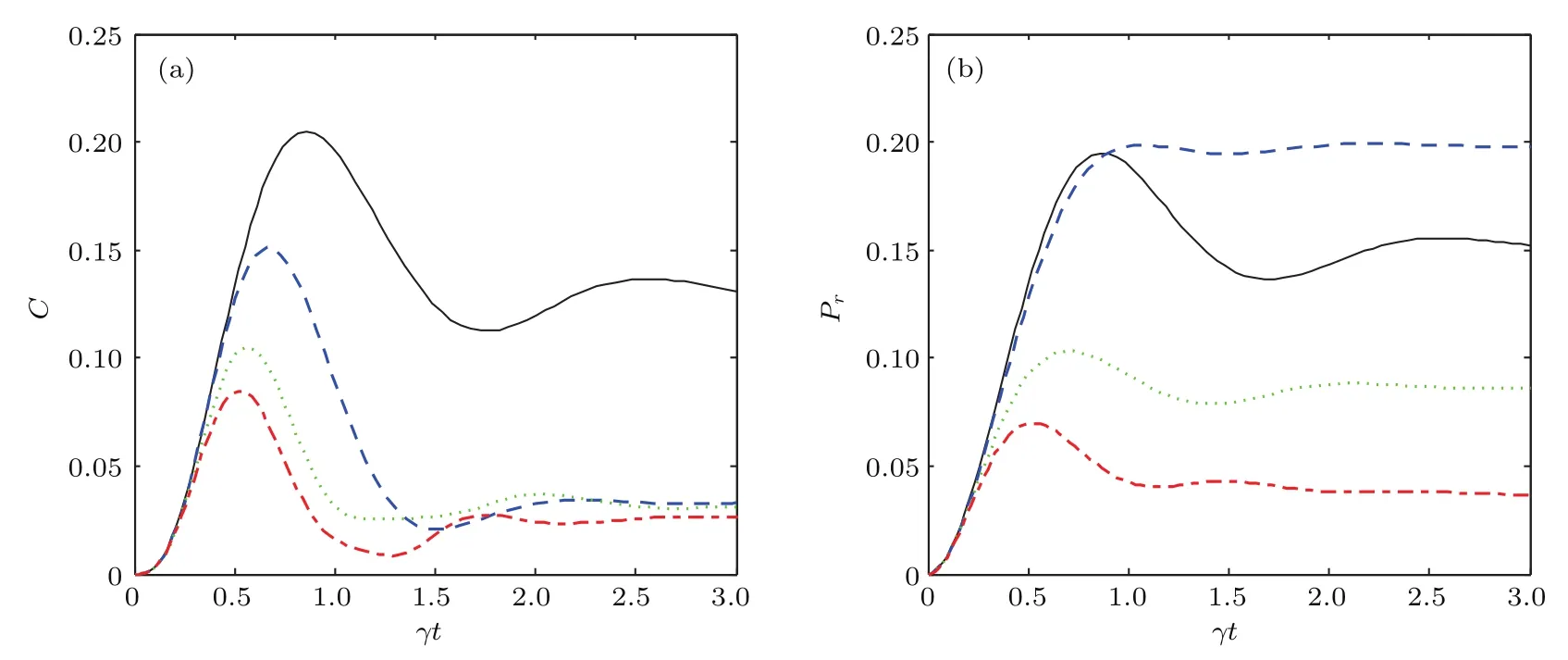
图6(a)共生纠缠C和(b)单原子激发概率Pr的时间演化曲线(黑色实线、蓝色折线、绿色点线以及红色点折线分别对应于Δ/V=0,1/2,1,5/4的情况,其中偶极-偶极相互作用V/Ω =5)Fig.6.(a)Time evolution of concurrence C and(b)single-atom excitation probability Prwith dipole-dipole interaction V/Ω=5.The black solid,blue dashed,green dotted and dash-dotted curves correspond to Δ/V=0,1/2,1,5/4,respectively.
进一步讨论稳态纠缠、激发与单光子失谐的关系.从图5可以看出,当V/Ω=5时纠缠最大值出现在共振点,这正对应偶极阻塞效应.与独立原子系综不同,激发概率最大值会偏离共振点,这是因为偶极-偶极相互作用补偿正、负失谐的结果不同,导致差异化的原子激发行为.此外,还可以说明单原子激发概率与共生纠缠行为并没有严格的对应关系.
保持原子间偶极-偶极相互作用不变,讨论两种激发机制下对应的纠缠和激发概率的动力学演化.选取V/Ω=5意味着偶极-偶极相互作用强度中等,这样能够更好地观察系统的动力学演化.如图6(a)所示,初始时刻没有原子激发,所以纠缠也不存在.随着里德伯原子的激发,几乎所有原子都参与相互作用过程,因此纠缠逐渐增加并做集体拉比振荡,共振情况(偶极阻塞机制)下集体拉比振荡频率正比于,而失谐情况(偶极反阻塞机制)振荡频率高于共振情况,失谐越大,振荡频率越大,在γt≥3系统进入稳态.共振情况的纠缠峰值和稳态值均大于非共振情况,这与前面的提到的稳态结果一致.从图6(b)可以看出Δ/V=1/2时原子激发概率最大,这与稳态结果一致,也是失谐补偿了能级移动的结果.但是对应的纠缠却没有共振情况大,原因在于前者接近单激发集体态而后者则接近双激发集体态的原因. 对于失谐更大的反阻塞机制(Δ/V=1,5/4),单原子激发得不到满足,所以纠缠自然就很小,失谐越大,纠缠的峰值和稳态值就越小.
实验上可以选择三能级梯形结构Rb87原子,基态、中间激发态以及最高能级分别为和60S1/2, 一方面让的跃迁为大失谐,另一方面保持经到里德伯能级60S1/2的跃迁为双光子共振,即采取双光子激发方案,这样原子可以等效为二能级原子.进而通过样品中原子间平均距离来测算原子间的范德瓦耳斯势V=ħC6/R6,其中C6和R分别为范德瓦耳斯系数和原子间距.再调整大失谐获得有效的拉比频率,使得V/Ω和Δ/γ的数值满足研究的参数范围.最后,测量里德伯原子的激发概率和测算共生纠缠的大小.
5 结 论
本文讨论了稀薄气体中的量子纠缠和里德伯激发性质.以空间排布为正四面体的少体原子系综为模型,同时计及原子间偶极-偶极相互作用.通过精确的数值计算来考察系统在偶极阻塞和反阻塞机制下的稳态和瞬态动力学性质.结果表明,里德伯激发决定着量子纠缠,无论是稳态和瞬态,偶极阻塞机制下的共生纠缠度都是最大.进一步考察高阶激发过程,分析了两种机制下的纠缠类型并给出物理解释.
[1]Gallagher T F 1994 Rydberg Atoms(Cambridge:Cambridge University Press)
[2]Saffman M,Walker T G,Mølmer K 2010 Rev.Mod.Phys.82 2313
[3]Comparat D,Pillet P 2010 J.Opt.Soc.Am.B 27 A208
[4]Jaksch D,Cirac J I,Zoller P,Rolston S L,Côté R,Lukin M D 2000 Phys.Rev.Lett.85 2208
[5]Lukin M D,Fleischhauer M,Côté R,Duan L M,Jaksch D,Cirac J I,Zoller P 2001 Phys.Rev.Lett.87 037901
[6]Tong D,Farooqi S M,Stanojevic J,Krishnan S,Zhang Y P,Côté R,Eyler E E,Gould P L 2004 Phys.Rev.Lett.93 063001
[7]Porras D,Cirac J I 2008 Phys.Rev.A 78 053816
[8]Pedersen L H,Mølmer K 2009 Phys.Rev.A 79 012320
[9]Gorniaczyk H,Tresp C,Schmidt J,Fedder H,Hofferberth S 2014 Phys.Rev.Lett.113 053601
[10]Tiarks D,Baur S,Schneider K,Dürr S,Rempe G 2014 Phys.Rev.Lett.113 053602
[11]Pritchard J D,Maxwell D,Gauguet A,Weatherill K J,Jones M P A,Adams C S 2010 Phys.Rev.Lett.105 193603
[12]Vogt T,Viteau M,Zhao J,Chotia A,Comparat D,Pillet P 2006 Phys.Rev.Lett.97 083003
[13]Ye S,Zhang X,Dunning F B,Yoshida S,Hiller M,Burgdörfer J 2014 Phys.Rev.A 90 013401
[14]Labuhn H,Barredo D,Ravets S,de Léséleuc S,Macrì T,Lahaye T,Browaeys A 2016 Nature 534 667
[15]Gillet J,Agarwal G S,Bastin T 2010 Phys.Rev.A 81 013837
[16]Fan C H,Yan D,Liu Y M,Wu J H 2017 J.Phys.B:At.Mol.Opt.Phys.50 115501
[17]Lee T E,Häffner H,Cross M C 2011 Phys.Rev.A 84 031402
[18]Lee T E,Häffner H,Cross M C 2012 Phys.Rev.Lett.108 023602
[19]Šibali N,Wade C G,Adams C S,Weatherill K J,Pohl T 2016 Phys.Rev.A 94 011401
[20]Dauphin A,Müller M,Martin-Delgado M A 2016 Phys.Rev.A 93 043611
[21]Petrosyan D,Otterbach J,Fleischhauer M 2011 Phys.Rev.Lett.107 213601
[22]Yan D,Liu Y M,Bao Q Q,Fu C B,Wu J H 2012 Phys.Rev.A 86 023828
[23]Gärttner M,Whitlock S,Schönleber D W,Evers J 2014 Phys.Rev.Lett.113 233002
[24]Carmele A,Vogell B,Stannigel K,Zoller P 2014 New J.Phys.16 063042
[25]Weber T M,Höning M,Niederprüm T,Manthey T,Thomas O,Guarrera V,Fleischhauer M,Barontini G,Ott H 2015 Nat.Phys.11 157
[26]Zeiher J,Schauß P,Hild S,Macrì T,Bloch I,Gross C 2015 Phys.Rev.X 5 031015
[27]Liu Y M,Tian X D,Wang X,Yan D,Wu J H 2016 Opt.Lett.41 408
[28]Ates C,Pohl T,Pattard T,Rost J M 2007 Phys.Rev.A 76 013413
[29]Hill S,Wootters W K 1997 Phys.Rev.Lett.78 5022
[30]Wootters W K 1998 Phys.Rev.Lett.80 2245
[31]Yan D,Song L J 2010 Acta Phys.Sin.59 6832(in Chinese)[严冬,宋立军 2010物理学报 59 6832]
[32]Ates C,Pohl T,Pattard T,Rost J M 2007 Phys.Rev.Lett.98 023002
[33]Amthor T,Giese C,Hofmann C S,Weidemüller M 2010 Phys.Rev.Lett.104 013001
[34]Honer J,Löw R,Weimer H,Pfau T,Büchler H P 2011 Phys.Rev.Lett.107 093601

