一元二次函数零点分布问题新探

张宏斌

（重庆市铜梁中学校，重庆）

一元二次函数是高中解题的基础，高中阶段几乎所有章节的数学问题，都可以与其结合，是历年高考永恒的主题。而现阶段初中教学降低了对一元二次函数的要求，学生对其图象性质把握不好，特别是对其零点的分布问题认识不深入。教学中我发现不少同行虽然也用数形结合对零点进行分析，但不透彻，甚至有些教学资料上将零点细分为多达八九种类型，不便于学生掌握。本文仍用数形结合的思想，把一元二次函数零点分布（亦即一元二次方程根的分布）问题总结为两种主要类型，便于学生把握其本质，提高解题效率。

定义1.同一范围：根所处的区间端点没有把两个根分开，称根分布在不同范围内。

定理一.根在同一范围时，需要列：

例 1.二次方程 ax2+bx+c=0（a＞0）二根 x1，x2均在区间（m，n）内，怎么列式？

解：记f（x）=ax2+bx+c。由题做出图1，结合一元二次函数图象开口方向、对称轴、图象所经过的特殊点，容易列出如下不等式组。

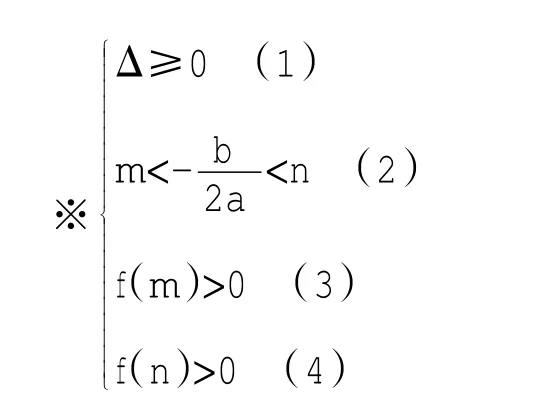
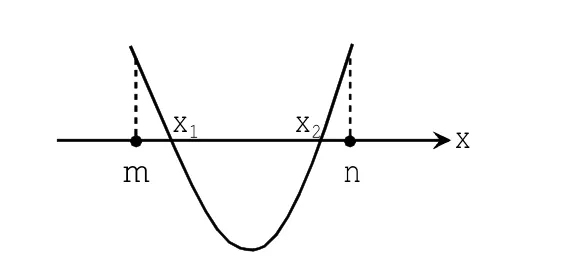
图1

若不等式组※缺少任何一个不等式，均得不到图1。即不等式组※是题目成立的充要条件。四个不等式、三种条件缺一不可。

定义2.不同范围：根所处的区间端点，将两个根分开，称根分布在不同范围内。

定理二.根在不同范围时，只需列：端点函数值的正负。

区间的端点有几个就要列几个不等式，需全部考虑完整。

例 2.二次方程 ax2+bx+c=0（a＞0）二根 x1，x2满足 m＜x1＜x2＜n，又怎么列式？

作图2或图3，因为轴的位置与m，n的关系不明确，可列出如下不等式组：

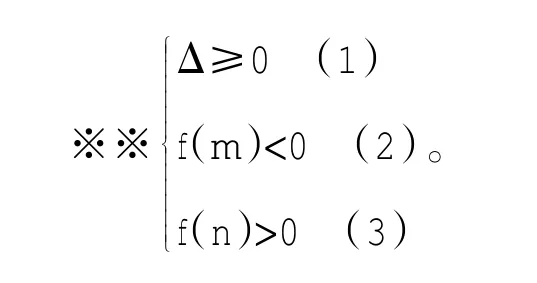
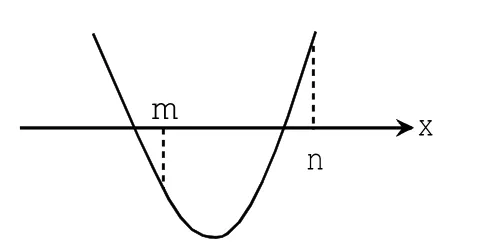
图2

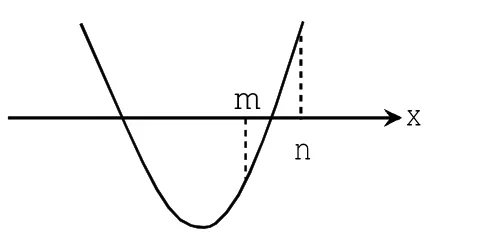
图3

仔细研究函数图象发现：①开口向上；②f（m）＜0，f（n）＞0，自然二次函数图象穿过x轴，所以不必要列判别式也可以得到m＜x1＜x2＜n，自然对称轴也不需要列了。仅（2）（3）两式就可做出图2或图3，和原题等价。

由上例1和例2，简单证明了定理一、二。

例3.关于x的方程x2-mx+2m-1=0满足下列条件，分别求m的取值范围。

（1）一根小于-1，一根大于2；

（2）一根在（0，2）内，一根在（3，5）内；

（3）二根均大于2；

（4）二根均在（-4，0）之间

（5）在区间（2，+∞）上无实根。

解：记f（x）=x2-mx+2m-1

（1）（2）均是根的不同范围分布，只列端点函数值得正负：

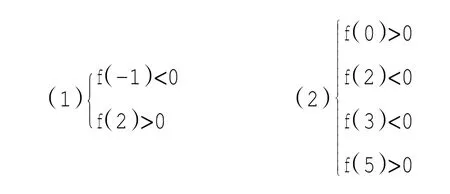
（3）（4）均是根的相同范围分布，需列判别式、轴、端点函数值正负三种类型：

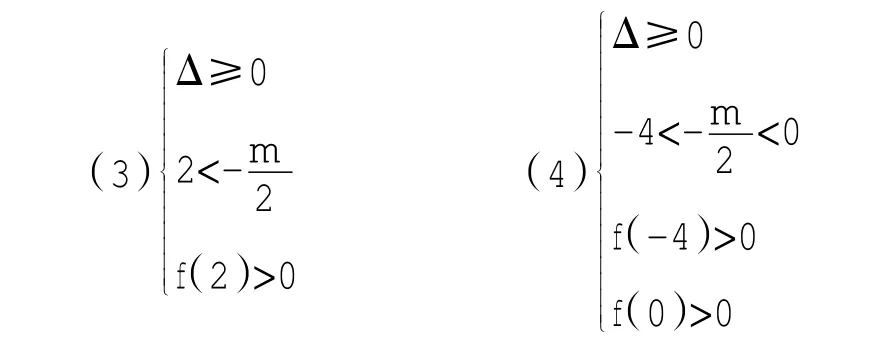
（5）方程要么无解，要么解都在（-∞，2］内：

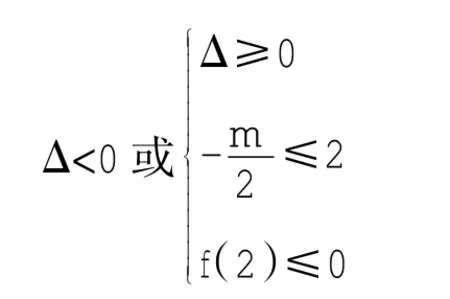
特别注意的是，区间端点的开、闭对所列不等式可否取等号的影响，多用数形结合分析讨论。

例4.二次方程2x2-（m+1）x+m=0有且仅有一实根在（0，1）内，求 m取值范围。

此题容易作出如下图4、5的形式，列出下式：

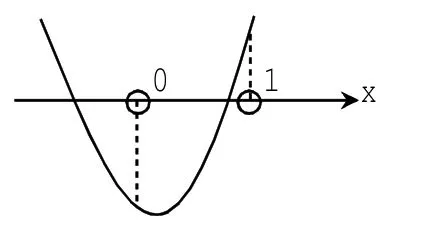
图4

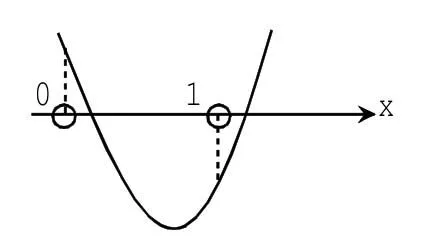
图5

函数图象也可能过x=1或x=2这两点，即为图6或图7，就有f（1）=0或f（0）=0

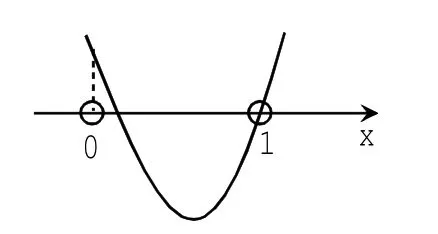
图6

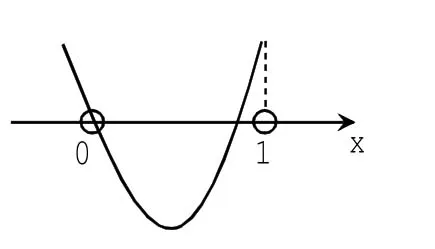
图7

但仅将上式（1）添个等号：f（1）·f（0）≤0，结果也不等价，如图8，在区间内就无解了。

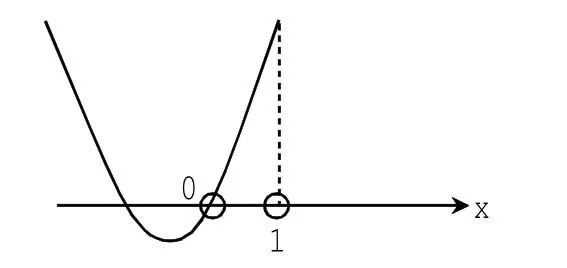
图8

实际上图6、7应归结为根的相同范围分布，要考虑轴靠近哪个端点，即轴与比较大小，综合图 6、7，应列出如下式子：

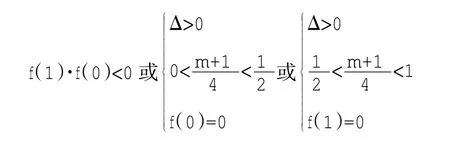
有没有更简洁的方法呢？实际上等号的问题就是担心图6到图8的情形，可直接算f（1）=0或f（0）=0，用算出的m再求根，检验根是否满足题目就行了，结果f（0）=0时成立，f（1）=0时不成立。

如此一来，关于在某区间内仅有一解的问题就有两种解法了：①归结成相同范围和不同范围，当穿过端点时讨论轴与端点中点的大小关系。②当作不同范围解，结合图象检验端点函数值为0时是否符合要求。第二种能简化计算。

数形结合是解决根分布问题的捷径，紧紧抓住一元二次函数的3个图象性质，将一元二次函数零点分布问题总结为分布在相同范围或分布在不同范围两种基本类型，遇到区间内仅有一解的问题多用检验端点函数值为0时根是否满足题意，可简化运算。