思维在探究中呈现 素养在活动中发展——以“空间几何体的外接球问题”为例

方泽英

（广东第二师范学院番禺附属中学，广东 广州）

高中数学复习课在高中数学的学习过程中占有很大的比重，特别是在高三的学习过程中。可以说，高三一年都是围绕高中所学的内容及知识点展开复习。传统的高三复习课流程大致如下：（1）大部分教师采用“先用10~15分钟的时间进行知识回顾，再结合相关题型进行例题讲解”；（2）以填空的形式让学生在课前完成知识梳理部分，课上进行题型的强化训练。以上两种复习课教学流程都是我们比较熟悉、常见的模式。虽然教师在课前花费了很大的力气进行备课、选题、做题，但复习效果往往不佳，达不到预设的效果。究其原因在于，这种传统的课堂复习模式突出了教师的主导地位，学生对知识梳理以及知识网络的建构相对被动，教师在教学中只是完成从知识到知识的简单传授，题型的强化训练也只是起到巩固、强化知识点的作用，达不到就针对的高考考点进行专题训练。因此，这样的复习课对学生能力提升是不够的，不利于发展学生的学科素养。

结合近年来教育领域研究的热点“核心素养”，所谓的数学素养是学生应具备的适应终身发展和社会发展需要的数学领域的必备品格和关键能力。从培养学生数学核心素养的角度来看，传统的复习模式显然不利于培养学生的学科素养。如何在复习课中渗透学科素养呢？笔者认为教师的教学要从基本概念入手，帮助学生理解概念的内涵和外延，创设情境引导学生回归基础、回归知识本质的学习，在学生的探究活动中开拓思维，渗透学科素养。本文以“空间几何体的外接球问题”的专题教学为例，讨论基于数学核心素养下的教学设计，希望能起到抛砖引玉的作用，供同行交流学习。

一、教材分析

立体几何是高中数学的重要内容，而空间几何体的外接球问题更是高考考查的重点内容。笔者就近10年来高考全国卷对立体几何考查的题型及知识点进行分析，发现试题的考查基本上稳定在三道题，两小一大，小题常考两种类型，一种主要以三视图为载体，考查学生的空间想象能力，另一种就是球的内容，属于中档题。主要是通过球这个载体考查学生的空间想象能力及推理运算能力。基于本节课内容在高考中的重要性及高三一轮复习的特点，本节课设计的着眼点注重理解球心概念，注重从探究常规图形（如正方形和长方形）外接球的球心位置及半径；到探究有条棱垂直于底面，且垂点是顶点时空间几何体的外接球的球心位置及半径；最后到探究所有棱长都相等或对棱相等的三棱锥的外接球的球心位置及半径。以上三种探究内容均是历年高考考查的重点内容。因此，本节课有必要针对这三种形式的内容展开专题教学，引导学生回归知识本质的学习，总结解题的通法。

二、学情分析

虽然空间几何体的外接球内容在高一时已涉及，但由于我校学生基础较为薄弱，对空间几何知识的储备及空间感的想象能力有限，加上高考是以球为载体来考查学生的空间想象能力及推理运算能力。对学生来说是一个难点，主要体现在：（1）学生能够想象到图形，但要画出其草图，难度较大；（2）即使能够把图画出来，由于在空间中，学生难以找到球心的位置，半径是多少也无法得知。既然球的有关问题是高考考试的重点内容，所以在高三复习教学中，空间几何体的外接球问题的教学应该引起我们重视，我们有必要在教学中结合学生的认知特点和高三一轮复习的特点，深入研究高考全国卷命题者的出题方向和命题意图，设计专题学案，逐层深入，帮助学生建构知识体系，结合历年高考的考题特点适当补充和拓展相关知识，注重知识理解和技能提升，采取学生课前预习、合作探究、启发学习等形式，调动学生的学习兴趣，培养和提高其数学思维能力，帮助学生构建空间几何体的外接球的学习框架。

三、教学设计目标及思路

本课的设计目标是：（1）通过探究空间几何体的外接球问题的解决培养学生数学抽象、逻辑推理、数学建模、直观想象以及数学运算等数学核心素养；（2）通过空间几何体的外接球问题的解决的数学活动，培养学生解决数学问题的意识与能力，提升学生的数学思想，使四基落实到数学课堂中；（3）通过空间几何体的外接球问题的解决，让学生巩固球的相关知识及基本的数学思想方法。

本课的设计思路：以特殊、常见的空间几何体的外接球问题作为问题情境，通过问题串的形式，将教学难点分解、细化，层层深入，由浅入深，由易到难。学生通过小组合作探究、交流展示的形式，逐步从探索的问题中抽象出数学问题，归纳总结出常见的空间几何体的外接球问题的求解通法，并利用所归纳的通法尝试求解高考题，从而提升学生分析问题和解决问题的能力。

四、教学过程

1.课前任务

（1）将班级的同学平均分成8个小组。

（2）提前完成学案的“知识回顾”“合作探究”。

2.讲授过程

第一环节：知识回顾

问题1：球心定义：_______________________________。

问题2：球的表面积和体积公式：S球面=____________V球=__________。

问题3：三角形正弦定理：_______________________________。

以上三个问题在课堂上直接请三位同学口答，教师重点引导学生明确求解球的核心问题在于确定球心位置及求出球的半径。

★设计意图：创设问题情境，引发学生兴趣，导入本课学习；检测学生课前学习情况，了解学生知识薄弱的地方，及时生成资源，为求解球的有关问题做好知识铺垫。

第二环节：合作探究

合作探究一：

（1）已知正方体ABCD-A1B1C1D1的棱长为a，且它的8个顶点都在同一个球面上，求这个球的半径？

（2）已知长方体 ABCD-A1B1C1D1的长、宽、高分别是 a，b，c，且它的8个顶点都在同一个球面上，求这个球的半径？

（3）已知三棱锥P-ABC的四个顶点都在球O的表面上，已知PA⊥面ABC，AB⊥AC，如何求这个球的半径？

（4）已知三棱锥P-ABC的四个顶点都在球O的表面上，已知PA⊥面ABC，AB⊥BC，如何求这个球的半径？

（5）已知三棱锥P-ABC的四个顶点都在球O的表面上，已知PA⊥面ABC，△ABC为等边三角形，如何求这个球的半径？

教师通过课前的学案检查，反馈学生做题过程中存在的问题，并提示做题的关键，以小组为单位，由学生进一步自主合作探究，寻求解决问题的突破口。以抽签的形式选出5个小组，再请各小组派代表展示思维过程，教师进行点拨、讲解。最后师生共同将其归类，总结提炼出解题通法。

★设计意图：正方体和长方体的外接球的球心是在其体对角线的中点处，这是绝大部分学生都能接受的知识。从学生容易接受的最简单的情形开始考虑，能激发学生的求知欲，也能让绝大多数的学生参与探究。随着问题的深化，当正方体和长方体变成三棱锥时，并且有条棱垂直于底面，且垂点是顶点时，学生能不能利用补形的方法，将三棱锥外接球的问题转化为长方体或正方体外接球问题呢？可以让不同水平的学生展示各自的思维水平和数学素养水平，而且随着困难的增加也能展示各类学生在解决问题中的意志品质。通过设计一系列的问题串来启发学生找到在解决不同情形下的问题共性，师生共同提炼解题通法，可以培养学生从具体到一般的思维过程。同时，通过小组合作探究，交流展示，不仅能够充分调动学生学习的主动性，也能让学生在学习的过程中学会与人交流合作，培养学生的数学表达能力。

合作探究二：

（6）已知正四面体 P-ABC，所有棱长都相等，点 P，A，B，C 都在球O的表面上，如何求这个球的半径？

（7）已知正三棱锥P-ABC，点P，A，B，C都在球O的表面上，顶点P到面ABC的距离为h，底面△ABC外接圆的半径为x，如何求这个球的半径？

（8）已知三棱锥 A-BCD，AB=CD=a，AD=BC=b，AC=BD=c 则三棱锥A-BCD外接球的半径？

教师通过课前的学案检查，反馈学生做题过程中存在的问题。结合课堂上学生在合作探究一中所得到的解题思路及求解方法，以小组为单位，由学生再进一步自主合作探究，寻求解决问题的突破口。再从剩下的3个小组中，选派代表展示思维过程，教师进行点拨、讲解。最后师生共同将其归类，总结提炼解题通法。

★设计意图：学生在小组合作探究一中获得了求解一类空间几何体外接球问题的基础上，教师抛出合作探究二的三个问题，可以进一步激发学生的求知欲望，培养学生学以致用的意识。引导学生在剖析问题时，尝试学会将不规则的空间几何体的外接球问题转化为规则图形（正方体或长方体）的外接球问题，培养学生数学建模思想，转化和化归思想。最后，师生共同总结提炼解题通法，有助于培养学生的数学概括、数学抽象能力，有利于学生逻辑思维的整理和条理化。

第三环节：题组训练

题组一：

1.（2017年广州学考16）《九章算术》是我国古代内容极为丰富的数学名著，书中把“底面为直角三角形的直棱柱”称为堑堵。今有一堑堵，其高为2，底面直角三角形的斜边长为4，则该堑堵的外接球的表面积为 。

2.（2009年全国卷1，理15）直三棱柱ABC-A1B1C1的各顶点都在同一球面上，若AB=AC=AA1=2，∠BAC=120°，则此球的表面积等于 。

3.已知△EAB所在平面与矩形ABCD所在平面互相垂直，EA=EB=3，AD=2，∠AEB=60°，则多面体E-ABCD的外接球的表面积为 。

4.（2018年广州调研，文12，理16）如下图，网格纸上正方形小格的边长为1，图中粗线画出的是某三棱锥的三视图，则该三棱锥的外接球的表面积为 （ ）

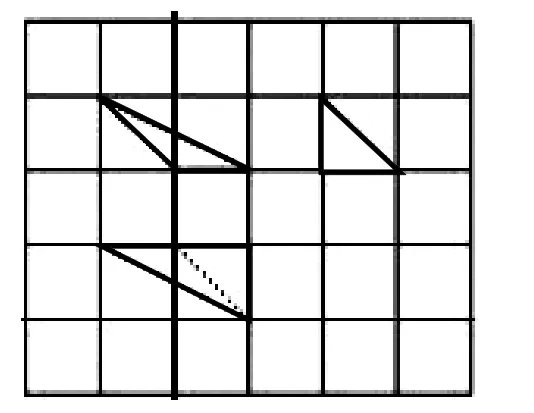
5.已知正方形AP1P2P3的边长为2，点B、C分别为边P1P2、P2P3的中点，沿 AB、BC、CA 折叠成一个三棱锥 P-ABC（使 P1、P2、P3重合于点P），则三棱锥P-ABC的外接球体积为 （ ）

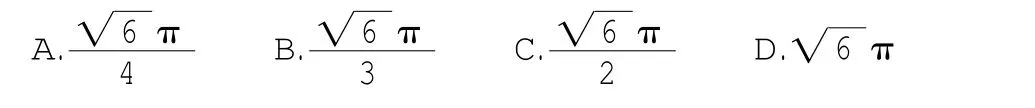
★设计意图：选自学考、调研考、高考的试题作为题组的典型例题，分别从不同角度来考查空间几何体外接球的相关问题，让学生能够运用得到的解题通法，在具体的问题情境中快速地进行数学建模，合理选用公式求解，体验学以致用的快乐，增强解题信心。

题组二：

1.（2014年全国大纲，文10）正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为 （ ）

A.3π B.4π

3.（2012年辽宁，理16）已知正三棱锥P-ABC，点P，A，B，C都在半径为的球面上，若PA，PB，PC两两垂直，则球心到截面ABC的距离为 。

4.（2012年全国卷1，理11）已知三棱锥S-ABC的所有顶点都在球O的求面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC=2，则此棱锥的体积为 （ ）

5.在三棱锥 A-BCD，AB=CD=2，AD=BC=3，AC=BD=4，则三棱锥A-BCD外接球的体积 。

★设计意图：学生在题组一的求解过程中获得解题信心，激发了学生的求知欲望，再给出题组二的五个题目，可以让学生进一步尝试用探究得到的解题通法运用在具体的问题情境中，体验学以致用的快乐，消除求解空间几何体外接球问题的恐惧心理。

第四环节：回顾反思

1.数学知识方面

★设计意图：首尾呼应，加深学生对本节课探究内容的理解及所得到的各类解题通法的总结，有利于学生形成知识网络体系。

2.数学思想方法：数形结合、化归与转化、解方程思想

（1）长方体或正方体的外接球的球心是在其体对角线的中点处。

（2）对于常见的不规则的几何体外接球问题可以将不规则的几何体补成正方体或长方体来求解，化繁为简。具体图形如下：

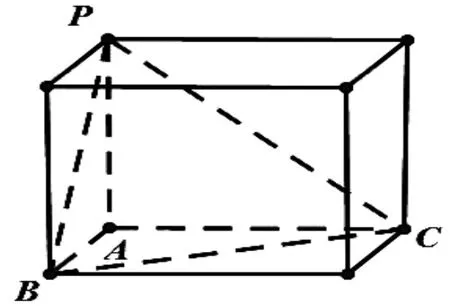
三条侧棱两两垂直的三棱锥三个侧面两两垂直的三棱锥某一个顶点上的三条棱两两垂直的三棱锥（侧棱垂直于底面1）

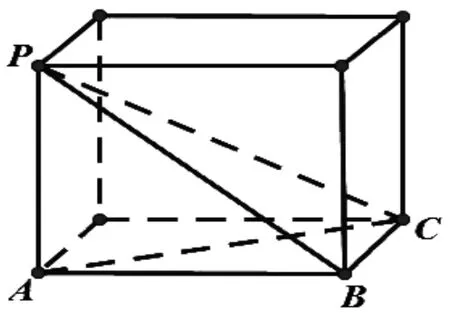
四个面都是直角三角形的三棱锥（侧棱垂直于底面2）

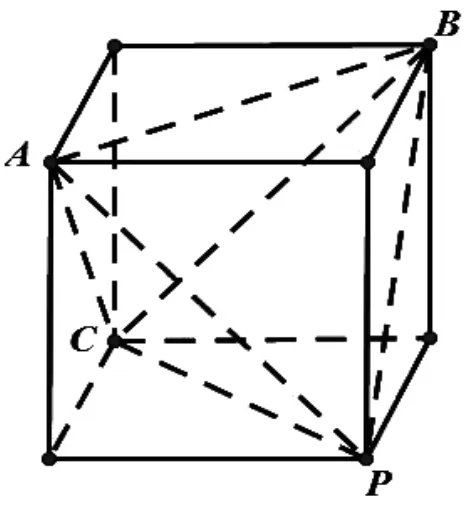
正四面体

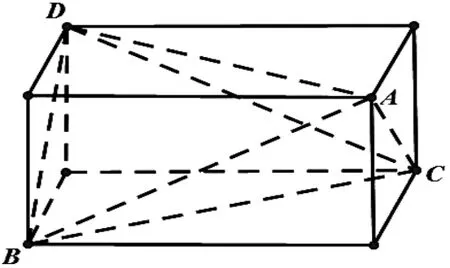
相对的棱相等的三棱锥

★设计意图：数学解题的关键在于回归基础，回归本质。在解题中不断强化学生将不熟悉的问题转化为熟悉的问题，复杂的问题转化为简单问题，不断提升学生分析问题、解决问题的能力。

第五环节：布置作业（略）

五、课后反思，引领教学

1.优化问题设计，渗透学科素养

课改的目的是：从根本上转变学生的学习方式和教师的教学方式，提倡自主学习、合作学习、探究式学习和研究性学习，使学生掌握终身必备的基础知识和学习方法；教师由单纯的教学者转变成学习型、研究型的教师，教学中，教师是学生学习的指导者、参与者和合作者。这两种转变需要“量”的积累过程。因此，在课改的形势下，本课从尊重学生的主体地位、弘扬学生的个性发展入手，探索在数学复习课中渗透学科素养。首先，本课倡导将课堂还给学生的理念，在教学形式上突破传统课堂“满堂灌”形式，以学生为主体开展活动。如课前学生的自主预习、合作探究、小组展示等形式，都能较好地激发学生参与课堂活动的积极性和有效性，提高课堂教学的有效性，在师生活动、生生活动中培养学生的学科素养。其次，在本课结构的设置上，大胆打破教材框架，突破常规，围绕高考常考题型进行设计，采用一系列问题串的形式，将教学难点分解、细化，层层深入，由浅入深，由易到难，引导学生进行合作探究，交流展示，逐步从探索的问题中抽象出数学问题，提升学生分析问题和解决问题的能力。最后，在教学环节的设计上，注重每一个环节的小结，让学生尝试进行总结、提炼，有助于培养学生数学概括、数学抽象的能力，有利于学生逻辑思维的整理和条理化。除此之外，本课的设计强调课堂的小组合作，重视学生数学思维品质和口头表达能力的培养，在学生的合作交流活动中发展学科素养。

2.编排典型题组，提升解题能力

高三数学复习课有两个任务：一是梳理概念，形成网络；二是提升能力，拓宽思维。本课作为高考第一轮复习的内容，在抓好以上两方面内容的同时，注重结合高考常考知识的特点，设计空间几何体外接球专题学案，设计一系列符合学生认知特点的探究问题，通过师生的共同活动得到解题通法。在典型例题的强化训练上，本课采用“题组训练”的形式，打破传统的让学生直接进行解题的强化训练，而是在学考、调研考、高考等试题中，选择同一类型但不同考查方向的题目作为题组的典型例题进行针对性教学。在题目的求解方式上，教师先让学生对题组的问题进行分析、求解，再结合教师的点拨、讲解，把题目讲活，让学生通彻，明白问题的诸多变化，以及万变不离其宗的道理。引导学生挖掘题目的内涵价值、拓展试题的外延范围，从而实现做一道题，会一类题，提升解题能力。让学生通过“知识问题化”得到的思想方法应用在“题组训练”中，使学生的思维一直处于活跃期，让学生亲身经历数学活动的过程，获得感性的认识和体验，提升理性的思维，从中获得数学意识、数学能力和数学素养。