多面体三视图的还原策略

李 珍

（广东省惠州一中实验学校，广东 惠州）

直观想象作为高中数学学科核心素养之一，在教学中期望进一步发展学生几何直观和空间想象能力。学好三视图的还原有助于提高学生的空间想象能力和综合分析能力。同时，三视图还原一直是高考的重点和难点。本文针对大部分同学不擅长的多面体还原给出还原直观图的方法，让学生有迹可循，进而达到落实数学核心素养的目的。

根据三视图的基本概念和投影规律，并结合教学经验给出如下多面体三视图还原的操作步骤：

1.确定载体。根据三视图确定几何体的载体为长方体还是正方体。

2.消线定点。根据正、俯、侧视图删除不需要的线（或用其他颜色标出表明多面体的顶点不能落在此线上），确定需要的顶点。

3.成图检验。连接顶点，检验还原后的几何体和已知三视图是否对应。

例1 将如图1-1所示的三视图还原成几何体。

步骤1：根据三视图的长、宽、高确定载体为正方体，见图1-2。

步骤2：根据正视图，删除不需要的线，见图1-3；根据俯视图，删除不需要的线，见图1-4。

根据侧视图，删除不需要的线，见图1-5；根据侧视图，确定多面体的顶点，见图1-6。

步骤3：连线成图并检验，明确几何体为三棱锥E-BCC’，见图1-7。

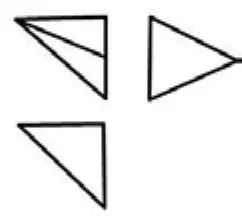
图1-1

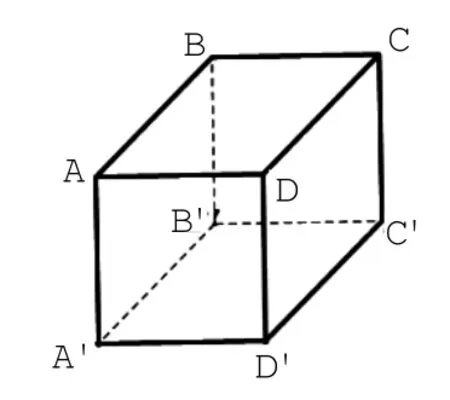
图1-2

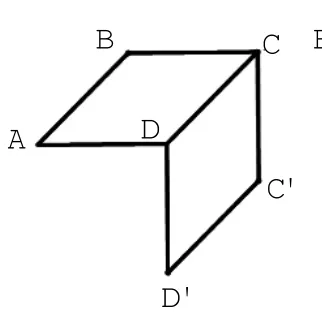
图1-3

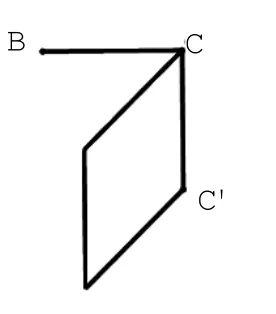
图1-4

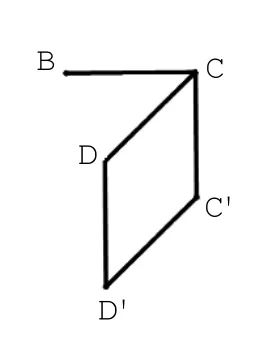
图1-5

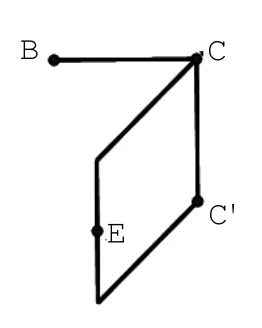
图1-6

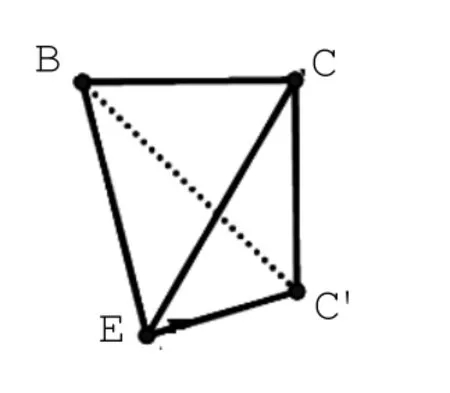
图1-7

例2 将如图2-1所示的三视图还原成几何体。

步骤1：根据三视图的长、宽、高确定载体为正方体，见图2-2。

步骤2：根据正视图，删除不需要的线，见图2-3；根据俯视图，删除不需要的线，见图2-4；根据侧视图，确定多面体的顶点，见图2-5。

步骤3：连线成图并检验，明确几何体为三棱锥B-DD’C’，见图2-6。

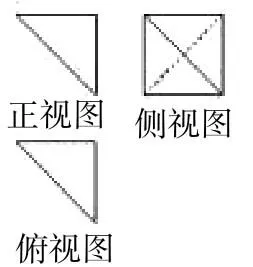
图2-1

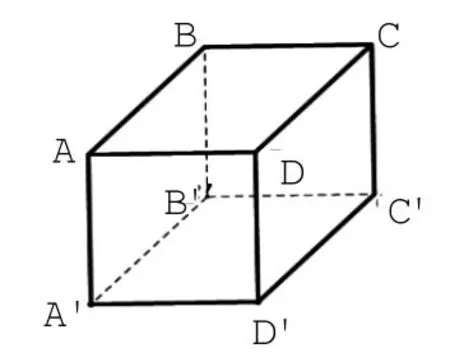
图2-2

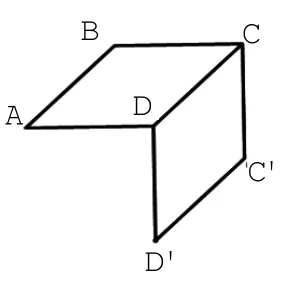
图2-3

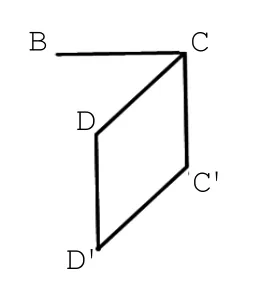
图2-4

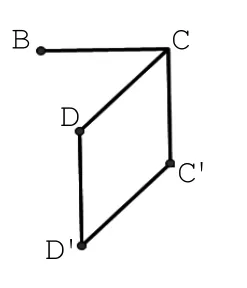
图2-5

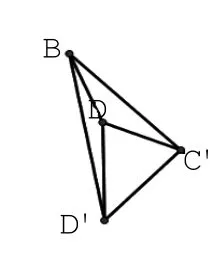
图2-6

例3 将如图3-1所示的三视图还原成几何体。

步骤1：根据三视图的长、宽、高确定载体为长方体，见图3-2。

步骤2：根据正视图，删除不需要的线，并根据正视图、俯视图，确定多面体的顶点，见图3-3。

步骤3：连线成图并检验，明确几何体为平行六面体A’B’F’E’-EFCD，见图3-4。

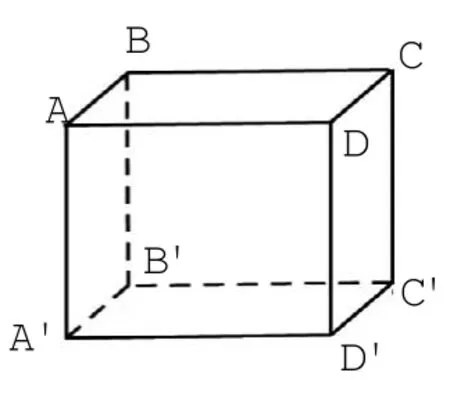
图3-2

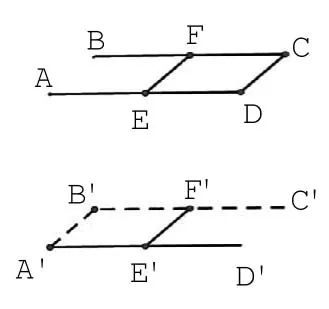
图3-3

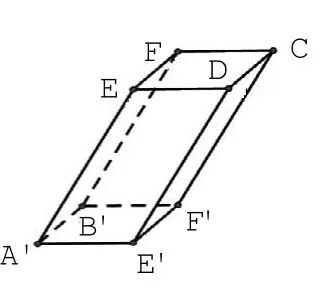
图3-4

总之，在应对多面体三视图还原几何体这一类问题时，以学生最为熟悉的正方体或长方体作为载体，利用正投影原理进行消线定点，直观形象，简单快捷，大大提高了学生的解题效率。