一种综合型FPGA布局算法

王新晨，许 慧，虞 健，惠 锋

（1.中国电子科技集团公司第五十八研究所，江苏无锡 214072;2.无锡中微亿芯有限公司，江苏无锡 214072）

1 引言

现场可编程逻辑门阵列(Field-Programmable Gate Array,FPGA)近年来越来越多地应用到各种各样的场合，其可实现的功能越来越多，电路的规模也越来越大。电子设计自动化 (Electronic Design Automation,EDA)工具在FPGA的应用中起着关键作用，FPGA的快速发展也对EDA工具提出更高要求。EDA的主要流程有综合、打包、布局、布线、仿真验证、位流下载等。

布局是影响EDA工具运行速度及电路最终质量的关键一步，它将布局网表中的逻辑单元一一映射到芯片的实际位置。现有的主流算法中，模拟退火算法[1]可以以1的概率逼近全局最优解，但较为缓慢；二次线性规划算法[2]虽然能快速得出结果，但往往在解的质量上逊色不少。单一使用一种算法已不能快速有效地解决布局问题，许多取长补短的结合型算法因此出现。本文结合了二次线性规划算法和模拟退火算法并做出了一些改进，力求能够快速有效地解决布局问题。

2 综合型算法概述

本文提出的综合型算法流程如图1所示，首先使用二次线性规划算法，利用该算法快速得到解的特性，快速迭代得到一个较优的布局情况。该算法使各逻辑单元相对均匀地分布在电路中并保持了较优的相对位置，但这个结果往往占用电路面积较大。这时再使用模拟退火算法，因为已经有了一个相对较好的布局情况，模拟退火算法不必从高温开始迭代退火，而是选择一个较低的温度，使算法快速收敛。这样结合使用两种算法，既获得了较高质量的解，又保证程序较快的运行速度。

图1 综合型算法流程图

3 二次线性规划算法及改进

二次线性规划算法是一种解析型算法，使用数学的方法求解矩阵，以得到理论的最优解。该算法把所有的布局逻辑单元看作节点，把所有节点之间的信号关系建立成点到点的边的关系即力，并以此建立矩阵，用一种类似于“弹簧伸缩”的方式迭代优化布局状态。如图2所示，方格表示芯片上一定范围的区域，该区域可容纳一定数量的单元，布局的过程中允许出现放置单元超出容量的情况，即形成overlap，迭代过程不断降低overlap，并最终通过合法化过程将overlap消除。

图2 节点移动过程图

图2中空心圆代表某次解矩阵后节点所在的位置，首先进行展开的过程，将节点按照密度均衡的原则移动至虚线圆点处，同时对每个节点加一个新的力，此时同一个区域内的节点相对于其相应边界距离的伸缩比例相同，但实际移动距离和施加的力却不同，且其施加的力不能使节点在此位置保持力平衡[3]。

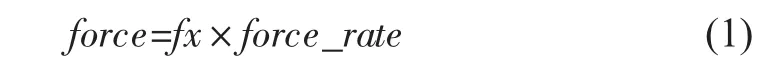
如式（1）所示，施加的新力force等于实际移动距离 fx与 force_rate之积，force_rate由当前区域的overlap情况决定，overlap越大，force_rate越大。

在下一次解矩阵后，力重新回到平衡状态，由于各节点之间的连接关系不同，其收缩的力也有不同，各节点因而又各自移动了不同的距离。图2中实心圆即表示重新回到力平衡状态后节点的位置。

在实际运用中，特别是一些中、大规模电路中，往往有许多连接关系十分紧密的节点，它们从第一次解矩阵开始即分布在相同的位置，此后的伸缩过程也由于其紧密的关系导致每次伸缩的距离大致相同，节点之间的相对位置很难拉开，甚至合法化过程开始前依然处于同一个区域中。这样关系紧密的节点越多，算法过程中overlap降低得越慢，合法化过程开始前的overlap率越高。这样既影响了速度，也影响了质量。

本文的算法在计算新施加的力时进行了区别对待，对于overlap小的区域，仍然按照原有公式计算，对于overlap大的区域，则在原有公式的基础上加入一个扰动，见式（2）：

其中α代表所加的扰动，在操作每个适用区域时，α首先取一个很小的值，然后每对一个节点加力后，α就随之增大，但也始终保持在一个较低的值。这样一个小的扰动既不会破坏原有节点间的相互关系，又可以使overlap加速变小，使节点分布更加均匀，从而在一定程度上提高了布局的质量。

4 模拟退火算法及改进

模拟退火算法是一种基于启发式搜索的算法，它通过设置一个评价函数来评定当前解的情况，并通过不断迭代达到优化的目的。该算法分为内外两层循环：每一次内循环中，电路逻辑单元会进行若干次位置交换，每次交换都使用评价函数进行评估，然后判断是否接受；每一次外循环都会更新温度、交换半径等控制参数，当温度达到一定低值时，退火过程结束，再进行若干次零温度迭代后算法结束。

初始温度是模拟退火算法的重要参数。传统的模拟退火算法使用一个随机的布局作为初始状态，在这个初始状态的基础上进行若干次交换，求取其评价值的标准差，再计算出初始温度，如式（3），T0即为初始温度[4]。

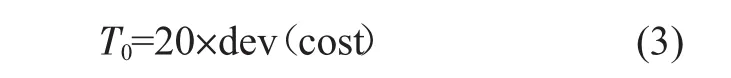
T0往往是一个很高的温度，在这个温度下几乎所有的交换都被接受，从而保证了模拟退火算法足够大的解空间。但在结合型算法中，模拟退火算法前已经使用二次线性规划算法获得了一个较优的解，这时再使用高温退火会使布局情况再度变得无序，破坏了二次线性规划的结果。因此，本文提出的结合型算法使用式（4）计算 T0。

其中β由内迭代的规模决定，内迭代次数每上升一个数量级，β就下降一个数量级，当内迭代次数为10时β为2。

除了温度，模拟退火算法中另一个重要的控制参数是交换半径。传统模拟退火算法在外循环中设置交换半径来约束交换的范围，最初交换半径为芯片长度，之后，交换半径随着温度下降而变小，直至降为1。这样的交换半径变化配合温度的变化，既可以保证足够的解空间，又可以使算法逐渐收敛。

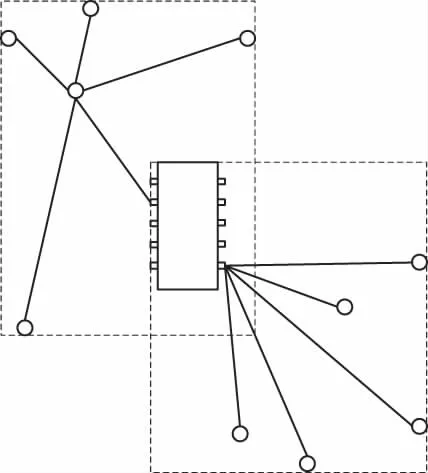
图3 交换范围示意图

由于综合型算法中的模拟退火算法紧跟二次线性规划算法后使用，且已经对初始温度的计算做出修改，所以传统的交换半径计算方法也需要做出改变。本文算法在内循环中确定被选中单元的交换范围，而不是传统模式的在外循环中统一设置。如图3所示，被选中的交换单元有若干连接有线网的引脚，线网所连的其他单元用空心圆表示，图3中虚线框恰好包含了一个线网的所有单元，称为这个线网的边界框。交换时，首先与传统模拟退火算法相同，随机选取一个要交换的单元，然后随机选取被选中单元的一个有线网连接的引脚，获取该引脚所在线网的边界框，边界框中的位置无论是否已有单元放置均为候选的位置，只需随机选择一个即可。

5 实验结果及讨论

本文随机选取了10个MCNC测试集中的电路，在Xilinx的xc5vlx330ff1760器件上分别使用本文提出的改进的结合型算法和原版结合型算法进行布局。设置quadratic重叠率5%或迭代次数达到1000次时退出迭代，测试结果如表1和表2所示。

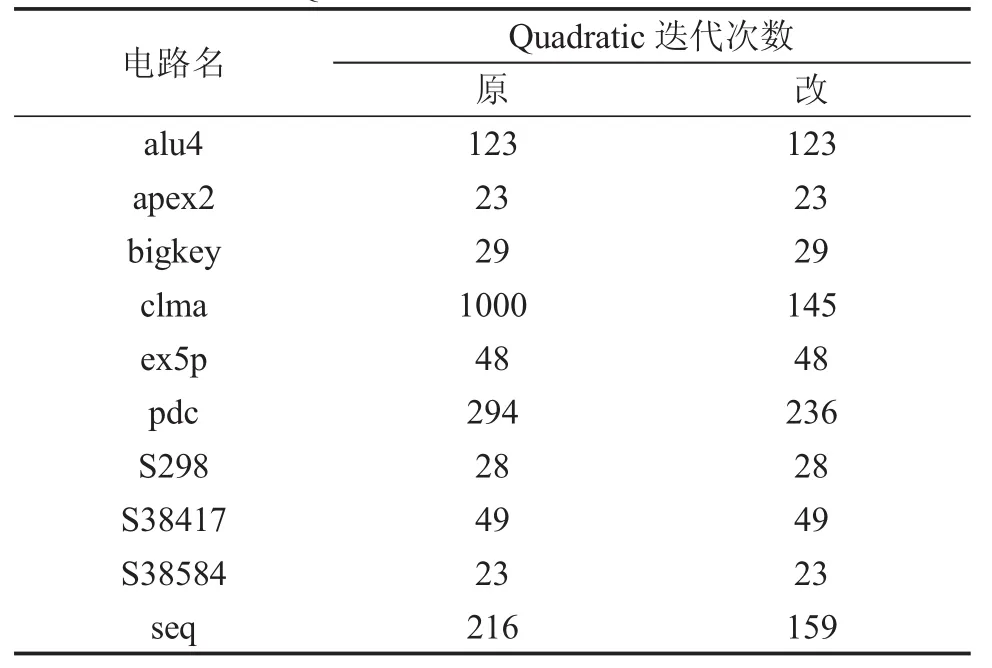
表1 Quadratic迭代次数测试结果表

从表1中可以看出，对原本迭代次数就比较少的电路来说，对quadratic的改进并不能造成影响，但对于迭代次数较多的电路却有可观的提高，尤其对于电路clma，在原版中该电路因达到迭代上限1000次而退出迭代，即原算法已不能使该电路有效展开，而在改进算法后只需145次迭代即可达到要求，迭代次数的减少即代表时间的减少。

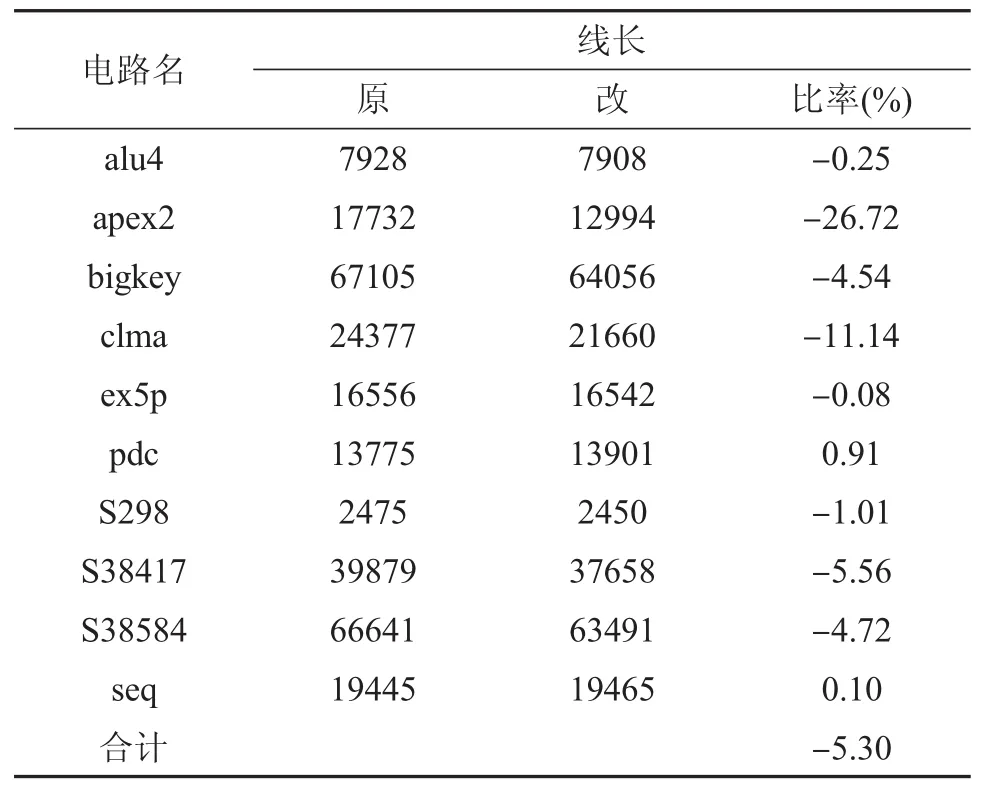
表2 布局后预估线长测试结果表

此外，如表2所示，使用线长来评估电路质量，可以看到改进后算法获得了平均5.30%的提升。

6 结论

本文提出的综合型算法在二次线性规划算法和模拟退火算法上分别做出了改进，使得算法可以在较短的时间内给出质量较高的布局结果，解决了现有的FPGA布局算法单独应用于布局问题时或需要耗费太长时间、或不能给出质量较高解的问题。

[1]Metropolis,N A,A Rosenbluth.Equation of State Calculations by Fast Computing Machines[J].Journal of Chemieal Physies,1953,21:1087-7092.

[2]Myung-Chul Kim,Dong-Jin Lee,Igor L Markov.SimPL:An Effective Placement Algorithm[M].University of Michigan,2005.

[3]虞健.FPGA布局算法应用研究[D].武汉：武汉理工大学,2011.

[4]Vauglm Betz,Jonathan Rose.VPR:A New Packing,Placement and Routing Tool for FPGA Research[C].InternationalWorkshop on Field Programmable Logic and Applications,1997.