一类积分号外具有非常数因子的弱奇异时滞积分不等式

覃炜达, 王五生

(河池学院 数学与统计学院, 广西 宜州 546300)

Gronwall[1]和Bellman[2]为了证实微分方程解对参数的连续依赖性研究了积分不等式

其中c≥0是常数,得到了未知函数的估计

(1)

由于Gronwall-Bellman型积分不等式是研究微分方程、积分方程解的存在性、有界性、稳定性和唯一性等定性性质的重要工具,人们不断地对它的形式进行了各种推广,使它的应用范围不断地扩大.文献[3-6]及其引文研究了具有连续积分核的积分不等式;文献[7-14]及其引文研究了具有奇异积分核的积分不等式.为了证实抛物型柯西问题解的全局存在和指数衰减结果,Henry[7]研究了线性奇异积分不等式

Ye等[8]讨论了积分号外具有非常数因子的线性奇异积分不等式

利用复杂的幂级数给出了未知函数的估计.为了用显式界表示不等式中未知函数的估计,Medved[9]给出了另一种类似于经典Gronwall-Bellman不等式中未知函数估计的方法.最近,Ma等[11]用改进的Medved方法研究了弱奇异积分不等式

f(s)uq(s)ds,t∈[0,+∞).

(2)

受文献[9,11]的启发,本文研究了积分号外具有非常数因子的非线性奇异时滞积分不等式

f(s)uq(s)ds,t∈[t0,+∞).

(3)

不等式(3)把文献[11]中的不等式(2)推广为时滞不等式.为了研究这个时滞弱奇异不等式(3),首先证明了具有时滞的Hölder积分不等式,然后给出了一类幂形式积分不等式中未知函数的估计,接着得到了时滞弱奇异不等式(3)中未知函数的估计.最后举例说明了本文结果可以用来研究分数阶积分方程解的性质.

1 主要结果与证明

成立.假设函数α(t)是区间[t0,+∞)上的连续、可微、单增函数,且有α(t)≤t,α(t0)=t0,则

(5)

证明不等式(4)是经典的Hölder不等式，不需要证明.利用经典的Hölder不等式(4)可以推出

(6)

故Hölder不等式中积分上限是满足引理条件的函数时也成立.

引理2[10-11]令a≥0,p≥q≥0和p≠0,则对任意K>0有

(7)

引理3[11]令β、γ、ξ和p都是正常数,则

t∈[0,+∞).

(8)

假设函数α(t)是区间[t0,+∞)上的连续、可微、单增函数,且有α(t)≤t,α(t0)=t0,则

t∈[0,+∞),

(9)

引理4[11]假设正常数β、γ、ξ、p1、p2满足下列条件之一:

1)β∈(0,1],γ∈(1/2,1),ξ≥3/2-γ,p1=1/γ;

2)β∈(0,1],γ∈(0,1/2],ξ>(1-2γ2)/(1-γ2),p2=(1+4γ)/(1+3γ),

则对i=1,2都有

θi=pi[β(γ-1)+ξ-1]+1≥0.

(10)

引理5[11,14]假设函数u(t)、η(t)、θ(t)、h(t)都是区间[0,+∞)上的非负连续函数,q≥1,则不等式

t∈[0,+∞)

(11)

中的未知函数有估计式

t∈[0,+∞),

(12)

其中

(13)

引理6假设函数u(t)、η(t)、θ(t)、h(t)都是区间[t0,+∞)上的非负连续函数,q≥1,t0≥0,函数α(t)是区间[t0,+∞)上的连续、可微、单增函数,且有α(t)≤t,α(t0)=t0,则不等式

t∈[t0,+∞)

(14)

中的未知函数有估计式

t∈[t0,+∞),

(15)

其中

(16)

证明为了证明方便,先定义区间[t0,∞)上的函数

(17)

显然有v(t0)=0.求函数v(t)的导数,利用(14)和(16)式得

v′(t)=α′(t)h(α(t))uq(α(t))e(α(t))+

α′(t)h(α(t))uq(α(t))e(α(t))-

α′(t)h(α(t))θq(α(t))e(α(t))×

α′(t)h(α(t))uq(α(t))e(α(t))-

α′(t)h(α(t))θq(α(t))v(t)≤

[(α′(t)h(α(t)))1/qη(α(t))e1/q(α(t))+

(α′(t)h(α(t)))1/qθ(α(t))×

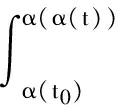
α′(t)h(α(t))θq(α(t))v(t)≤

[(α′(t)h(α(t)))1/qη(α(t))e1/q(α(t))+

(α′(t)h(α(t)))1/qθ(α(t))×

α′(t)h(α(t))θq(α(t))v(t)≤

[(α′(t)h(α(t)))1/qη(α(t))e1/q(α(t))+

(α′(t)h(α(t)))1/qθ(α(t))v1/q(t)]q-

α′(t)h(α(t))θq(α(t))v(t).

(18)

不等式(18)两边积分,由v(t0)=0得

η(α(s))e1/q(α(s))+

(α′(s)h(α(s)))1/qθ(α(s))v1/q(s))qds-

(19)

另一方面,根据Minkovsky不等式得

(α′(s)h(α(s)))1/qθ(α(s))v1/q(s))qds)1/q≤

(20)

由(19)和(20)式推出

(21)

根据v(t)和e(t)的定义,可得

(22)

(23)

由(23)式可得

(24)

把不等式(24)代入(14)式得到所要的估计式(15).

定理1假设函数u(t)、a(t)、b(t)、f(t)是区间[t0,+∞)上的非负连续函数,α(t)是区间[t0,+∞)上的连续、可微、单增函数,且有α(t)≤t,α(t0)=t0,p、q、β、γ、ξ都是正常数且有p≥q.如果未知函数u(t)满足不等式(3).

1) 假设β∈(0,1],γ∈(1/2,1),ξ≥3/2-γ;则对任意K>0,有未知函数的估计

(25)

其中

2) 假设β∈(0,1],γ∈(0,1/2],ξ>(1-2γ2)/(1-γ2),则对任意K>0有未知函数的估计

(26)

其中

注1不等式(3)、(25)和(26)中,令α(t)=t,t0=0,则得到文献[11]的结果.

证明把不等式(3)中的积分部分定义成函数w(t),即

f(s)uq(s)ds,t∈[t0,+∞),

(27)

则有

up(t)≤a(t)+w(t),

即

u(t)≤(a(t)+w(t))1/p,t∈[t0,+∞).(28)

利用引理2,对任意K>0由(28)式得到

uq(t)≤(a(t)+w(t))q/p≤

t∈[t0,+∞).

(29)

把(29)式代入(27)式得到

sξ-1f(s)w(s)ds,

(30)

其中

若β∈(0,1],γ∈(1/2,1),ξ≥3/2-γ,令p1=1/γ,q1=1/(1-γ);若β∈(0,1],γ∈(0,1/2],ξ>(1-2γ2)/(1-γ2),令p2=(1+4γ)/(1+3γ),q2=(1+4γ)/γ,则1/pi+1/qi=1对i=1,2都成立.利用引理1中的Hölder不等式,由(30)式推出

w(t)≤b(t)×

(31)

利用引理3和4,对任意t∈[t0,+∞),不等式(31)可以改写成

(32)

其中

(33)

θi(i=1,2)的定义在引理3中给出.利用引理6,对任意t∈[t0,+∞),由(32)式可得

[1-[1-Vi(t)]1/qi]-1×

(34)

其中

(35)

把p1=1/γ,q1=1/(1-γ)和p2=(1+4γ)/(1+3γ),q2=(1+4γ)/γ分别代入(34)和(35)式,再考虑关系式(28),得到所要证明的估计式(25)和(26).

2 应用

考虑下面的Volterra型分数阶积分方程

sβ(1+δ)-1yq(s)ds=f(t).

(36)

Ma等[11]研究了该方程在α(t)=t的情况.此类方程常常出现在各种实际问题中,特别是用来描述物理过程的后效性.

定理2假设函数y(t)和f(t)是区间[0,+∞)上的连续函数;α(t)是区间[t0,+∞)上的连续、可微、单增函数,且有α(t)≤t,α(t0)=t0;p、q、β、γ、δ是正常数,且p≥q.如果y(t)是方程(36)的解.

(i) 如果β∈(0,1],γ∈(1/2,1),β(1+δ)≥3/2-γ,则对任意K>0,有未知函数的估计

|y(t)|≤{|f(t)|+

(37)

其中

(ii) 如果β∈(0,1],γ∈(0,1/2),β(1+δ)>(1-2γ2)/(1-γ2),则对任意K>0,有未知函数的估计

|y(t)|≤{|f(t)|+

(38)

其中

证明由(36)式可以推出

令a(t)=|f(t)|,b(t)=|λ|t-βδ/Γ(γ),ξ=β(1+δ),利用定理1和Bernoulli不等式,

(1-x)1/z<1-x/z,

或

[1-(1-x)1/z]-10,z>0,

由(39)式得到所要证明的分数阶积分方程解的估计式(37)和(38).

致谢河池学院2016年硕士专业学位授予单位立项建设基金(2016YT003)对本文给予了资助，谨致谢意.

[1]GRONWALLTH.Noteonthederivativeswithrespecttoaparameterofthesolutionsofasystemofdifferentialequations[J].AnnMath,1919,20(4):292-296.

[2]BELLMANR.Thestabilityofsolutionsoflineardifferentialequations[J].DukeMathJ,1943,10(4):643-647.

[3]AGARWALRP,DENGS,ZHANGW.GeneralizationofaretardedGronwall-likeinequalityanditsapplications[J].ApplMathComput,2005,165(3):599-612.

[4] 王五生,李自尊. 一类新的非线性时滞积分不等式及其应用[J]. 四川师范大学学报(自然科学版),2012,35(2):180-183.

[5] 侯宗毅,王五生. 非线性三变量差分不等式及其应用[J]. 四川师范大学学报(自然科学版),2015,38(4):514-517.

[6]ABDELDAIMA.Nonlinearretardedintegralinequalitiesoftypeandapplications[J].JMathInequal,2016,10(1):285-299.

[7]HENRYD.Geometrictheoryofsemilinearparabolicequations[C]//LectureNotesinMath, 840.NewYork:Springer-Verlag,1981.

[8]YEHP,GAOJM,DINGYS.AgeneralizedGronwallinequalityanditsapplicationtoafractionaldifferentialequation[J].JMathAnalAppl,2007,328(2):1075-1081.

[9]MEDVEDM.AnewapproachtoananalysisofHenrytypeintegralinequalitiesandtheirBiharitypeversions[J].JMathAnalAppl,1997,214(2):349-366.

[10]JIANGFC,MENGFW.Explicitboundsonsomenewnonlinearintegralinequalitieswithdelay[J].JComputApplMath,2007,205(1):479-486.

[11]MAQH,PECARICJ.Somenewexplicitboundsforweaklysingularintegralinequalitieswithapplicationstofractionaldifferentialandintegralequations[J].JMathAnalAppl,2008,341(2):894-905.

[12] 欧阳云,王五生. 一类含有p次幂的非线性奇异Volterra-Fredholm型迭代积分不等式及其应用[J]. 四川师范大学学报(自然科学版),2016,39(2):209-213.

[13] 黄春妙,王五生. 一类含有求最大运算的非线性时滞Volterra-Fredholm型积分不等式[J]. 四川师范大学学报(自然科学版),2016,39(3):382-387.

[14]WILLETTD.Nonlinearvectorintegralequationsascontractionmappings[J].ArchRationMechAnal,1964,15(1):79-86.