VMD的时频特性及其在滚动轴承故障诊断中的应用

陈保家 聂 凯 刘浩涛 邱光银 汪新波 林 云

(1. 三峡大学 水电机械设备设计与维护湖北省重点实验室， 湖北 宜昌 443002；2. 三峡大学 机械与动力学院， 湖北 宜昌 443002)

滚动轴承振动信号中的非固有频率冲击成分代表故障征兆，对于早期故障，这种非固有频率的冲击往往很微弱，而且轴承发生故障时，其振动信号具有非线性、非平稳特性[1]，传统的傅里叶变换以信号可表示为不同频率的平稳正弦波的线性迭加作为前提条件，但缺乏对信号局部时频变化的精确描述．所以需要用时频域分析方法对信号进行诊断．

经验模态分解(Empirical Mode Decomposition，EMD)方法可将非线性、非平稳信号自适应分解成不同频段的本征模态分量(Intrinsic Mode Function，IMF)进而转化成平稳信号进行分析[2-3]，在滚动轴承故障特征提取上得到了成功的应用．Kedadouche等提出了一种基于EMD和Teager能量算子[4]结合最小熵反褶积的齿轮故障诊断方法，高强等利用EMD对滚动轴承故障信号进行后利用Hilbert变换进行包络解调得到包络谱，成功地提取滚动轴承内外圈故障特征频率[5]．但是由于EMD存在一些明显的缺点，EMD分解的分量之间容易出现模态混叠以及EMD存在着明显的端点效应，这大大制约着EMD在轴承故障诊断中的应用[6]．小波变换(Wavelet Transform)是一种时间窗和频率窗都可改变的时频局部化分析方法，它具有窗口大小固定但其形状可改变的特性．但由于选取合适的小波基函数难度非常大，同时小波分析必须人为选择分解层数，缺乏对信号处理的自适应性[7]，从而显得有很大的局限性．

变分模态分解(Variational Mode Decomposition，VMD)是Konstantin等[8]于2014年提出的一种自适应信号分解新方法，该方法在分解过程中通过循环迭代求取约束变分问题的最优解来确定分解得到的IMF的频率中心及带宽，从而有效地分离出信号的各个频率成分．与EMD和小波相比，VMD具有收敛快、鲁棒性高的特点，并在故障诊断领域得到了应用，通过VMD分解得到的各个IMF进行解调处理可有效提取故障特征，目前常用的方法有能量算子解调、希尔伯特包络解调等．

本文通过仿真信号对比分析了VMD、EMD和小波分解的噪声鲁棒性和抑制模态混叠能力，并将其应用于滚动轴承故障诊断实例当中，结果显示VMD在故障信号处理方面有优越性．

1 信号分解的仿真分析

VMD的分解过程是一种自适应求解约束性变分问题最优解的过程，通过循环迭代确定不同的频率中心及带宽从而将信号分解成不同的IMF分量．详细步骤可参考文献[8-9，11，12]．

1.1 仿真信号对比分析

为了研究VMD、EMD和小波变换的分析效果，采用以上3种方法分别对仿真信号进行分解，仿真信号x(t)由3个简谐信号加随机噪声组成，表达式为

x(t)=f1(t)+f2(t)+f3(t)+n(t)(1)

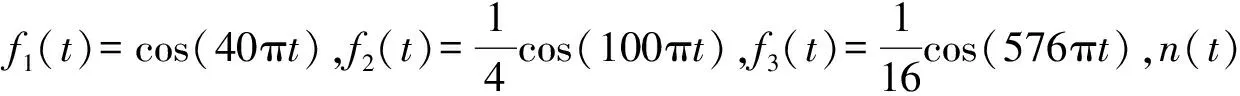
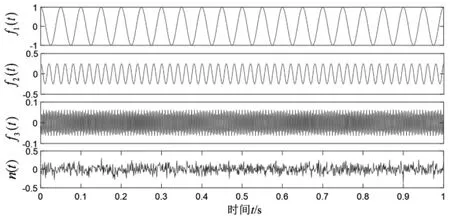
图1 含噪声信号的组成成分

选用db10小波对仿真信号进行3层小波分解，分解所得到的时域波形及其频谱如图2所示．从图中可看出，经过小波分解所得的各个分量中，没有出现频率为20 Hz的谐波分量，且分量中都存在一定的噪声干扰．图3为EMD分解结果，其中4个分量中已经分离出了3个对应的谐波分量，EMD分量中第4个分量和第3个分量对应的是20 Hz和50 Hz的谐波分量，含有少量的噪声成分，第1个分量对应的是288 Hz的谐波分量，但是噪声干扰严重，第2个分量是原始信号中没有的伪分量，对比图1中的原始分量波形，可以看出EMD分解的信号分量还存在不同程度的失真．总体来看，通过小波分解和EMD不仅很难辨识出原始信号中的谐波分量，而且噪声鲁棒性差．

图2 信号的小波分解

图3 信号的EMD分解

同样，利用VMD对x(t)进行分析，设定模态数k=4，所得到的时域波形及其频谱如图4所示，VMD的前3个IMF分量将原始信号的3个谐波分量从低频到高频都一一分解出来了，其中第1个IMF分量和第2个IMF分量与20 Hz和50 Hz的成分几乎相同，频谱非常干净无噪声，第3个IMF分量含有少量的噪声，第4个IMF分量为被分离出来的纯噪声．总的来看，VMD能够将原始信号的各组成成分与噪声成分进行有效分离，具有很好的噪声鲁棒性，结合各IMF分量的时域图和FFT谱，可以很容易推断原始信号x(t)的组成成分．

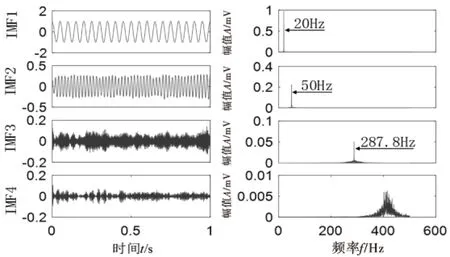
图4 信号的VMD分解

1.2 抗模态混叠性能研究

为了研究VMD的抗模态混叠性能．本节选用简谐信号与间断信号进行合成，用来模拟复杂信号中包含间断信号的情况．图5为信号各组成部分的时域图，合成信号y(t)的表达式为

图5 间断信号的各组成部分

其中，f1(t)、f2(t)与式(7)中的f1(t)、f2(t)相同，谐波分量f3(t)是间断信号，其表达式为

(3)

选用db10小波对y(t)进行3层小波分解，其结果如图6所示．第3分量和第4分量没有分解出频率为20 Hz和50 Hz的谐波，而且第2分量和第1分量有一定的模式混淆，并不能有效地分解出仿真信号的各个成分，由此可以看出小波在分解间断信号容易受到干扰．再利用EMD对y(t)进行分析，分解得到7个分量和一个残余信号．为图文简洁，取前4个分量如图7所示．

图6 信号的小波分解

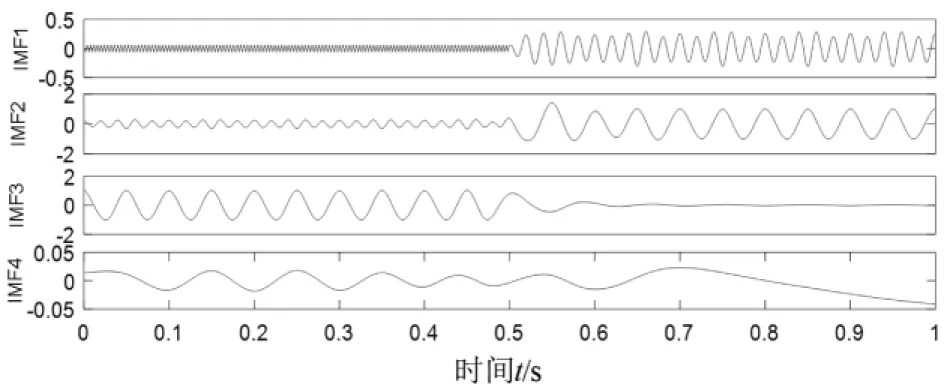
图7 信号的EMD分解

对比图5和图7可以看到，合成信号中频率为50 Hz和频率为250 Hz的成分被分解到IMF1中，而在IMF2中又出现了频率为50 Hz的中频成分，同样频率为20 Hz的低频成分也分别被分解到IMF2和IMF3当中，这说明经验模态分解存在严重的模态混叠，不能将间断信号准确分离出来．同样利用VMD对y(t)进行分析，设定模态数k为3，结果如图8所示，从图中可以看出VMD方法准确地将3个分量分离出来，特别是对于间断分量f3(t)的分解，仅仅只是在信号突变处出现了比较轻微的误差．通过对比可以发现，VMD比小波变换和EMD具有更好的抗模态混叠效果．

图8 信号的VMD分解

2 VMD滚动轴承故障诊断流程

通过以上分析，可以看出VMD方法摒弃了信号递归分解方式的束缚，采用一种非递归的、自适应搜寻策略对信号进行分解，因此相对于EMD和小波分解具有更好的噪声鲁棒性[9]和抗模态混叠效果，适合于从较低信噪比的轴承故障信号中将有用的特征信号分离出来，实现轴承的故障诊断．峭度指标是无量纲参数，由于它与轴承转速、尺寸、载荷等无关，对冲击信号特别敏感，当故障信号含有冲击信号时，峭度值会成明显的变化．本文采用VMD、Teager能量算子解调和峭度指标分量优选方法相结合，对滚动轴承故障信号进行分析，提取有效的故障特征，由于文献的篇幅限制，在此不再对Teager能量算子解调的基本原理进行展开叙述，详细的基本原理可以参考文献[4]．其诊断步骤如下：

1)获取振动信号，初始化模态数，令k=2．

2)对信号进行VMD分解，观察每个模态分量的中心频率．

3)判断中心频率是否相近，如果相近，则确定模态数k=k-1，否则以模态数k=k+1进行步骤2)，直到模态数设置合理．

4)通过峭度准则[10]对IMF分量进行筛选，选取出峭度值最大的模态，将其做为故障特征最敏感分量．

5)利用Teager能量算子解调[11]的方法对步骤4)中优选出的分量进行包络解调分析，求取分量包络谱．

6)将包络谱与故障特征频率进行匹配，判断故障类型．

3 诊断实例

3.1 滚动轴承故障数据获取

为了进一步验证该方法对滚动轴承故障诊断的有效性和实用性，文中选取美国Case Western Reserve University电气工程实验室轴承故障实验台采集的轴承故障振动信号进行研究分析．

试验台模拟滚动轴承4种状态：内圈故障、外圈故障、滚动体故障以及正常状态．本论文选取风机端的数据作为研究对象，轴承型号6205-2RS JEM，采样频率12 kHz，轴承转速r=1 797 r/min，转频为29.95 Hz．通过滚动轴承不同部件故障的特征频率计算公式可得：外圈故障频率fo=107.34 Hz，内圈故障频率fi=162.18 Hz，滚动体故障频率fb=119.42 Hz．

3.2 内圈故障分析

滚动轴承发生内圈故障时，滚动体经过故障点处会引起冲击振动，内圈转动时将产生周期性冲击[12]，内圈故障信号的时域和频域波形图如图9所示．先采用db10小波对内圈故障信号做4层分解，分解结果如图10所示．

图9 内圈故障的时频图

图10 信号的小波分解

从小波分量中并不能看出明显的故障特征，再根据峭度准侧选取峭度系数最大的分量为d1，对其进行Teager能量算子解调，其包络谱如图11所示．从图中可以看到内圈故障特征频率162 Hz和2倍频成分以及转频成分．接着采用EMD方法对内圈故障信号进行分解，共得到10个分量和一个残余分量，为了描述方便，给出了前6个IMF分量时域波形，如图12所示，同样峭度系数最大原则选取出最优分量为IMF1，对其进行Teager能量算子解调，其包络谱如图13所示，同样可以观察到内圈故障特征频率和2倍频成分，相比小波来说，非故障特征频率处的幅值较小，故障特征提取能力稍强，但是转频部分却没有凸显出来．

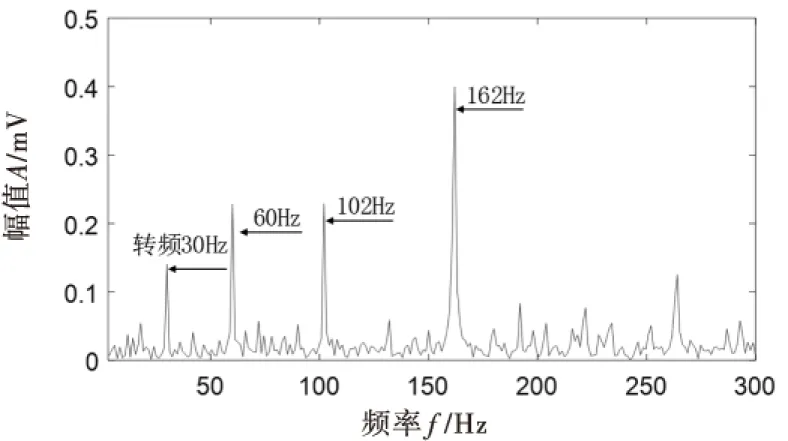
图11 小波分量能量算子解调

图12 信号的EMD分解

图13 EMD分量能量算子解调包络

最后采用本文的VMD方法对内圈故障信号进行分析，根据VMD算法提取信号特征最优原则，尽可能避免模态混叠同时保留信号的全部特征信息的情况下做了模态分量个数的对比分析[13]，当k取8的时候，分解得到的模态分量频带没有出现混叠，且分解得到的各分量频谱的幅值稍微偏高，特征信息频率的周围含有相对较少的噪声成分，因此在频域中特征信息部分更为凸显，由此可选择k=8，其分解结果如图14所示．利用峭度系数最大原则选出的最优分量为IMF4，对其进行Teager能量算子解调，得到包络谱如图15所示，图中可明显观察到轴承内圈故障特征频率162 Hz相近频率，且对比度很高，并且凸显出了轴承30 Hz的转频成分，有效地识别了故障特征频率，和内圈故障特性频率吻合，相比小波和EMD对噪声干扰性更小，但是这样并不能完全体现VMD的优势，接下来将在故障信号更微弱的滚动体实验里做分析，因为测得滚动体振动信号的传递路径复杂，且失效形式种类多样，因此故障特征更难被识别．

图14 信号的VMD分解

图15 VMD分量能量算子解调包络

3.3 滚动体故障分析

当滚动体表面出现局部损伤时，滚动体在深沟球轴承的内、外圈滚道之间除了存在滚动状态之外，还可能存在滑动状态，这种滑动将会掩盖调制故障特征，同时滚动体的损伤点在内、外圈并不是一直保持接触，因此滚动体故障的振动信号表现出更复杂的成分，故障特征表现得更加微弱，这也导致了目前诸多故障诊断方法都无法有效提取出深沟球轴承滚动体的故障特征频率[14]，为了凸显本文方法的有效性，将对滚动体故障信号进行分析．

图16为滚动体故障振动信号的时频谱，对滚动体故障信号进行小波分解、EMD分解及VMD分解，为图文简洁，在这里不再展示信号分解的分量图．采用db10小波对内圈故障信号做4层分解，通过峭度准则选取峭度值最大的d4分量进行Teager能量算子解调，得到如图17小波分量的能量算子解调包络．

图16 滚动体故障的时频图

图17 小波分量能量算子解调包络

从图中可看出包络中包含很多无关的频率成分凸显出来，完全无法提取出故障特征频率，同样采用EMD对滚动体故障信号做分解得到10个分量和1个残余分量，选取峭度系数最大IMF4分量进行Teager能量算子解调，得到如图18的包络图，包络中依然包含很多无关的频率，故障特征频率无法提取．

图18 EMD分量能量算子解调包络

最后采用本文的VMD方法能对滚动体故障信号进行分析，根据同上文的VMD算法提取信号特征最优原则，选择k=7进行7层分解，选取峭度系数最大的IMF6分量进行Teager能量算子解调，得到如图19所示的包络图，可以准确分解出滚动体的故障频率120 Hz，准确识别滚动体故障特征频率，但是小波、EMD以及VMD都没有分解出滚动体故障信号的基频，存在一定的不足．但是VMD可以准确分解出滚动体的故障频率，而使用小波和EMD分解的故障频率都被淹没在噪声里，没有有效地提取出滚动体故障特征频率，由此可见，VMD相比EMD和小波来说，可分解出更复杂更微弱的故障信号，对故障特性频率的提取有更大的优势．

图19 VMD分量能量算子解调包络

4 结 论

滚动轴承早期故障的振动信号受到强噪声干扰以及信号不规则性的影响，这些因素导致了其故障特征信息难以提取，针对此问题本文提出了一种基于VMD和Teager能量算子结合的故障诊断方法，并应用于滚动轴承的故障特征提取中，通过实验数据得出此方法的有效性及以下结论：

1)仿真信号分析结果表明，本方法能够在复杂的信号里有更有效的分解能力，且具备更强的抑制噪声干扰和抗模态混叠的能力．

2)本文提出的基于VMD的诊断方法对滚动轴承早期故障信号中的微弱特征信息能有效提取，准确判别了故障特征类型，相比传统的直接包络谱分析方法、EMD、小波等方法，分解效果更好，故障特征信息提取更明显．

[1] 邓飞跃．滚动轴承故障特征提取与诊断方法研究[D]．北京：华北电力大学,2016．

[2] Huang N E，Shen Z，Long S R，et al．The Empirical Mode Decomposition and the Hilbert Spectrum for Non-linear and Non-Stationary Time Series Analysis[J]．Proceedings of the Royal Society A Mathematical Physi-cal&Engineering Sciences,1998,554(1971):903-995．

[3] 杜秋华，杨曙年．经验模式分解的改进及其对球轴承缺陷的诊断[J]．振动、测试与诊断，2007，27(1):67-70．

[4] 李 辉，郑海起，杨绍普．基于EMD和Teager能量算子的轴承故障诊断研究[J]． 振动与冲击，2008，27(10):15-17，22，188．

[5] 高 强，杜小山，范 虹，等．滚动轴承故障的EMD诊断方法研究[J]． 振动工程学报，2007，20(1):15-18．

[6] 苏玉香，刘志刚，李科亮，等．一种改善EMD端点效应的新方法及其在谐波分析中的应用[J]．电工电能新技术，2008，27(2):33-37．

[7] 叶 昊，王桂增，方崇智．小波变换在故障诊断中的应用[J]．自动化学报，1997，23(6):736-740．

[8] Dragomiretskiy K，osso D．Variational Mode Decomposition[J]．IEEE Tran on Signal Processing，2014，2(3):531-544．

[9] 唐贵基，王晓龙．变分模态分解方法及其在滚动轴承早期故障诊断中的应用[J]．振动工程学报，2016，29(4):638-648．

[10] 蒲子玺，殷 红，张 楠，等． 基于峭度准则VMD及平稳小波的轴承故障诊断[J]． 机械设计与研究，2017，33(1):67-71．

[11] 马增强，李亚超，刘 政，等． 基于变分模态分解和Teager能量算子的滚动轴承故障特征提取[J]． 振动与冲击，2016，35(13):134-139．

[12] 王晓龙，唐贵基．基于变分模态分解和1．5维谱的轴承早期故障诊断方法[J]．电力自动化设备，2016，36(7):125-130．

[13] 郑小霞，周国旺，任浩翰，等．基于变分模态分解的风机滚动轴承早期故障诊断[J]．轴承，2016，41(7):48-53．

[14] 刘尚坤，唐贵基．改进的VMD方法及其在转子故障诊断中的应用[J]． 动力工程学报，2016，36(6):448-453．