基于灰色关联度的改进TOPSIS模型在水质评价中的应用

吴先明 蔡海滨 邓 鹏

(河海大学 水利水电学院， 南京 210098)

水质评价作为水环境质量评价的基础工作之一，采用合理科学的水质评价方法，能准确反映当前水体质量以及污染程度，弄清水体质量发展、变化的规律，为水环境治理提供支撑．目前，常用的水质评价方法主要有TOPSIS法、物元分析法、人工神经网络法、模糊综合评判法、单因子法[1-5]等．这些评价方法各有优缺点，例如单因子法[5]对于评价结果过于保护，以最差单项水质来代替整体水质，不能很好体现水体质量；人工神经网络法[3]收敛速度慢，对网络初始值较敏感．

TOPSIS(Technique for order preference by similarity to ideal solution)法[6]是目前常用的一种多目标决策方法，主要特点是由决策者定义理想方案和一种测度距离，根据各评价方案与该决策问题的正理想解和负理想解之间的测度距离大小来衡量该方案与理想解的偏差程度，因此该方法也常被称为理想解法．但传统的TOPSIS法仅考虑了方案与正、负理想解之间距离上的接近程度，并没有考虑形状上的相似关系．而且TOPSIS法基于原始数据，具有一定的客观性，如果在数据信息量较少的情况下使用TOPSIS法就可能得不到正确的决策结果．但是灰色关联分析法是从数据内部挖掘信息，通过分析各组数据与参考数据之间的几何曲线相似程度的大小来判定方案的优劣关系，而且它不需要大量数据，正好可以和TOPSIS法形成互补关系．目前对于这两种方法的组合使用也有学者进行研究，鲁方等[7]将灰色关联度同TOPSIS模型结合起来应用到接触带巷道支护方案优选上，选出综合最优的支护方案．李彦斌等[8]将灰色关联度与TOPSIS法结合起来对光伏发电项目进行综合评价，分析各项目风险值的大小从而为管理者提供决策支持．但是这些研究大多是通过对多方案进行比较选择最优方案，鲜有对待评价方案进行分级分类的研究．本文在现有研究的基础上，将欧式距离嵌入到灰色关联度的TOPSIS模型中，建立基于灰色关联度的改进TOPSIS模型，使模型不仅考虑各方案在距离上与理想解的接近程度而且还考虑形状上的相似关系，更显科学合理．同时本文引入组合赋权法来计算各项水质指标权重，克服了单一赋权的片面性，最后将本文所建模型应用于黄河下游的水质等级评价中，对该河段水质进行综合评价，得到了满意的效果．

1 指标权重的确定

多目标问题评价指标的权重确定通常有两种方法：一种是主观赋权法，指标权重由专家确定，有较强的主观性，但可以将一些复杂的赋权问题简单化，比较有代表性的包括AHP法，Delphi法[9]和环比系数法[10]等；另一种是客观赋权法，只关注数据内部本身的规律，不含人的主观喜好，如熵权法[11]、离差最大化法[12]等．本文将Delphi法和熵权法结合起来为各项水质指标赋权．

1.1 Delphi法确定指标权重

Delphi法[9]是一种主观赋权方法，以行业内经验丰富的专家对某一指标的评分为依据，充分发挥专家个人的知识储备优势对各项指标赋权．计算公式为：

(1)

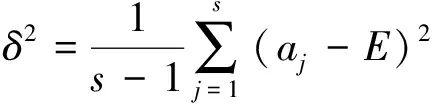
式中，E为某项指标的得分均值；aj为第j个专家对该项指标的评分结果；s为专家组总人数；δ2为方差，不仅反映该项指标得分发散程度，还体现了专家组成员对该指标看法的一致性程度．

采用Delphi法确定权重的公式为：

(3)

式中，αj为评价指标j的权重；Ej为指标j的实际得分．

1.2 熵权法确定指标权重

熵权法依据各项指标数据之间彼此关联程度或变异程度来确定指标的权重，该方法不掺杂评价者任何的主观因素．

对m个待评价的方案，每个方案均具有n项衡量优劣程度指标，则各方案的特征值矩阵可表示为X=(xij)m×n(i=1，2，…，m，j=1，2，…n)，熵权法的计算步骤如下：

1)对指标特征值矩阵用式(4)～(5)进行归一化处理得到相对优属度矩阵Yij=(yij)m×n

对于效益型指标

(4)

对于成本型指标

(5)

式中，sup(xij)、inf(xij)为同一项指标下各评价方案指标特征值xij中的最大值和最小值．

2)根据传统熵的概念，m个评价方案n项评价指标，可以定义评价指标j的熵为：

(6)

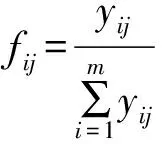
为了使fij有意义，一般假定当fij=0时，fijlnfij=0．当fij=1时，lnfij=0与实际情况不符，故对fij修正为：

(7)

3)将其中第j项评价指标的熵权βj定义为：

(8)

1.3 组合权重

单一的赋权法具有一定的局限性，目前国内学者对于主客观权重信息的集成也有一些研究，比如线性加权法[13]、最小偏差指标赋权法[14]等．因此本文采用简单的线性加权法将Delphi法计算出来的主观权重αj和熵权法计算出来的客观权重βj进行线性组合，其表达式如下：

ωj=μαj+(1-μ)βj(9)

式中0<μ<1，本文对于Delphi法和熵权法均没有偏好，故取μ=0.5．

2 基于灰色关联度的改进TOPSIS模型

2.1 模型建立步骤

1)将各待评价方案与水质分级标准的分界值构成增广决策矩阵，对增广决策矩阵X=(xij)m×n作标准化处理，得到标准矩阵B=(bij)m×n

(10)

其中i=1，2，…，m，j=1，2，…，n．

2)加权标准化矩阵U计算公式如下：

U=(uij)m×n=(ωjbij)m×n=

式中ωj为组合赋权法确定的各项评价指标权重．

3)确定加权标准化矩阵U的正理想解U+和负理想解U-．

(u+(1)，u+(2)，…，u+(n))

(u-(1)，u-(2)，…，u-(n))(12)

其中，J+是数值越大越好的"效益"型指标集合，如溶解氧含量等；J-是数值越小越好的"成本"型指标集合，如高锰酸钾指数等．

4)计算方案i与正理想解U+和负理想解U-在距离上的接近程度．

(13)

5)计算第i方案关于第j项指标与正、负理想解的灰色关联度．

式中，ε为关联系数，可取ε=0.5．

6)计算方案i与正理想解U+和负理想解U-在形状上的相似程度程度．

(15)

(16)

(17)

最后按改进相对贴近度的大小对评价方案进行分类分级，相对贴近度越大表明该方案与正理想解越接近，则方案越优；反之越劣．

2.2 水质分级评价流程

基于组合赋权法计算各项水质指标的权重后，通过对原始增广决策矩阵进行标准化处理，确定加权标准化矩阵和正、负理想解，分别计算各评价方案与正、负理想解距离上的接近程度和形状上的相似程度，确定各评价方案与正、负理想解的综合接近度，最后通过计算改进的相对贴近度来获得各评价方案水体所属水质级别，该水质分级评价模型的具体流程如图1所示．

图1 水质分级评价流程图

3 实例验证

以黄河下游某河段的水质评价为例，采用实测数据[15]，说明基于灰色关联度的改进TOPSIS模型在水质综合评价中的应用过程．

水质评价指标根据该河段主要污染因子来确定，分别是：DO(溶解氧)、CODMn(高锰酸钾指数)、NH3-N(氨氮)、COD(化学需氧量)、BOD5(五日生化需氧量)．水质评价标准采用现行的《地表水环境质量标准》(GB 3838-2002)，见表1；实际监测数据见表2．

表1 水质评价指标及标准分级 (单位：mg/L)

表2 评价指标的实测值 (单位：mg/L)

根据Delphi法权重计算方法，由公式(1)～(3)计算主观权重αj=(0.181 6，0.161 5，0.297 5，0.254 9，0.104 5)．

根据熵权法权重计算方法，由公式(4)～(8)计算客观权重βj=(0.148 8，0.161 1，0198 1，0.238 8，0.253 3)．

由公式(9)计算组合权重ωj=(0.165 2，0.161 3，0.247 8，0.246 8，0.178 9)．

将地表水质量标准(表1)中的水质分级标准的5组分界值作为5个判别样品与表2各断面的实际水质监测数据共同构建原始增广决策矩阵X=xijm×n，i=1，2，…，m，j=1，2，…，n；m=14，n=5．

根据公式(11)～(12)计算加权标准化矩阵U，得到正理想解U+和负理想解U-：

U+=(0.0533，0.0156，0.0113，0.0417，0.0078)

U-=(0.0130，0.1167，0.1735，0.1334，0.1296)

根据公式(13)～(17)计算结果列于表3．

表3 计算结果

为了验证本水质评价模型的可行性和正确性，将本文所得结果与采用物元分析法所得到的相关研究结论[15]进行对比，见表4．

表4 各断面所属类别对比

对比结果发现：除了断面1处本文建立的评价模型评价结果为Ⅱ类水，物元分析法为Ⅰ类水外，其余8个断面的综合水质评价结果均与用物元分析法评价结果一致．通过对该河流水质等级的评价，水质最差断面在断面1～3处，为Ⅱ类水，其余6个断面均为Ⅰ类水，说明该河段水质良好．对水质原始数据比较发现1号断面的氨氮含量明显多于3号断面，溶解氧含量也明显少于3号断面，而其余3项评价指标含量均相差不大，但是物元分析法分析出来1号断面水质优于3号断面，与实际情况不符，可能是因为物元分析法不好界定相邻水质级别处的分界值造成的．两种方法评价结果对比说明本文所建模型的可行性和优越性，而且，本文水质评价模型对水体质量的综合评判等级更显合理、客观，具有良好的实用价值．

4 结 语

根据地表水环境质量标准确定了河流水质的几项主要评价指标，采用Delphi法和熵权法组合赋权来确定各项水质评价指标权重，并建立了基于灰色关联度的改进TOPSIS法的水质综合评价模型，该模型不仅具有灰色关联分析的优点，可以反映在形状上各评价方案与最优方案的相似程度，而且还综合了欧式距离法在距离上表征各评价方案与最优方案的接近程度，使本文的相对贴近度更显合理．并将该水质评价模型应用到黄河下游，对该河段水质进行综合评价，发现与物元分析法评价的水质结果基本相同，证明了本模型的实用性和有效性．同时，该模型还可应用到多目标决策、方案优选、环境评价等多方面，具有广泛的应用前景．

[1] 张先起，梁 川，刘慧卿．基于熵权的改进TOPSIS法在水质评价中的应用[J]．哈尔滨工业大学学报，2007，39(10)：1670-1672．

[2] 门宝辉，梁 川．水质量评价的物元分析法[J]．哈尔滨工业大学学报，2003，35(3)：358-361．

[3] 宋国浩．人工神经网络在水质模拟与水质评价中的应用研究[D]．重庆：重庆大学，2008．

[4] 潘 峰，付 强．模糊综合评价在水环境质量综合评价中的应用研究[J]．环境工程，2002，20(2)：58-60．

[5] 尹海龙，徐祖信．我国单因子水质评价方法改进探讨[J]．净水技术，2008，27(2)：1-3．

[6] 艾正海．关于多目标决策问题的理想点法研究[D]．成都：西南交通大学，2007．

[7] 鲁 方，叶义成，张萌萌，等．基于Euclid距离和灰色关联度的改进TOPSIS模型接触带巷道支护方案优选[J]．化工矿物与加工，2016，45(4)：39-44．

[8] 李彦斌，于心怡，王致杰．采用灰色关联度与TOPSIS法的光伏发电项目风险评价研究[J]．电网技术，2013，37(6)：1514-1519．

[9] 李升泽，蒋蓉华．用Delphi实现基于AHP层次分析的KPI赋权研究[J]．计算机工程与科学，2008，30(2)：37-38．

[10] 刘敏豪，于兴康．DDDs与月环比系数联用推测医院药房药物用量的应用研究[J]．今日药学，2013(8)：529-531．

[11] 闫文周，顾连胜．熵权决策法在工程评标中的应用[J]．西安建筑科技大学学报(自然科学版)，2004，36(1)：98-100．

[12] 马永红，周荣喜，李振光．基于离差最大化的决策者权重的确定方法[J]．北京化工大学学报(自然科学版)，2007，34(2)：177-180．

[13] 徐泽水，达庆利．多属性决策的组合赋权方法研究[J]．中国管理科学，2002，10(2)：84-87．

[14] 闫书丽，肖新平．基于偏差最小化模型的多属性决策集成方法[J]．系統工程，2005，23(10)：73-76．

[15] 樊引琴，刘婷婷，李 婳，等．物元分析法在黄河水质评价中的应用[J]．水资源与水工程学报，2013，24(2)：166-169．