爆炸载荷作用下波纹夹芯板动力响应的数值模拟
朱 健,李飞鹏,李 鑫,曲运莲
(太原理工大学 a.力学学院,b.材料科学与工程学院,c.外国语学院,太原 030024)
由于金属夹心结构具有低密度、高刚度、吸能效果好等传统金属材料所不具备的优点,近年来被广泛用于航空航天、船舶、铁路交通等领域[1-2]。而对其力学行为的研究也成为该领域的一个热点课题。QIU et al[3]基于芯层的压缩响应时间远小于夹芯板的整体响应时间,建立了夹芯梁、圆板的理想刚塑性模型,并提出在冲击过程中将固支夹心梁和夹心圆板按照其结构响应的顺序分成3个渐进的阶段。XUE et al[4]对爆炸载荷作用下夹芯板和同样质量的实心板抗撞击性能进行了对比,以面板的厚度、芯层胞元的长跨比及相对密度等为目标参数,对具有角锥桁架、点阵结构芯层的夹芯板的进行了研究。CUI et al[5]采用冲击摆系统对点阵夹芯板进行了爆炸实验,分析了面板芯层的失效模式,并与朱峰等[6]所进行的蜂窝夹芯板的爆炸实验进行了对比。LI et al[7]研究了铝蜂窝夹芯板在爆炸载荷下的力学行为,表明夹芯结构的变形失效模式与炸药的比距离密切相关;当比距离较小时,结构将生产局部大变形甚至破坏。以上研究大多集中于蜂窝/泡沫等夹芯结构,而实际工程中,波纹夹芯板的使用更为广泛,如活动板房、高铁车厢等,而目前关于波纹板抗暴能力的研究相对较少[8-9]。HUANG et al[10]通过实验对水下爆炸载荷下波纹板的动力响应研究表明,与实体板相比,波纹板的最终挠度将明显减小,波纹板芯层的高度将影响结构的响应率。ZHANG et al[11]研究了聚合物泡沫填充波纹夹芯板的动力响应发现,在爆炸载荷下填充物能有效防止结构的断裂,从而提高结构的抗爆性能。
本文采用AUTODYN对爆炸载荷作用下波纹夹芯板的动力响应进行数值模拟,分析夹芯板在爆炸载荷作用下面板和芯层的变形响应过程,并分析面板、芯层的厚度和屈服强度对波纹板变形及能量吸收的影响。
1 材料参数及模型
1.1 材料参数
在数值分析中空气状态方程采用理想气体状态方程:
p=(γ-1)ρE.
(1)
式中:密度ρ=1.225×10-3g/cm3;γ=1.4;初始能量密度为2.068×105mJ/mm3.
炸药采用TNT,爆轰产物状态方程为JWL(Jones-Wilkins-Lee)状态方程:
(2)
式中:p为爆轰产物的压力;V为爆轰产物的相对比容;e为爆轰产物的比内能;R1,R2,C1,C2,ω为待拟合参数,具体炸药参数见表1.
面板和芯层均采用1200-H18铝,材料模型选择与应变率相关的Cowper-Symonds模型:
(3)
式中,C、P为应变率相关的常数,σ0为初始屈服强度。具体铝合金参数见表1.

表1 炸药和铝合金材料参数Table 1 Material property of TNT and aluminum alloy
1.2 计算模型
由于波纹板的对称性,只建立了1/4模型进行计算。图1和图2给出了芯层波纹的函数曲线及波纹板的计算模型。芯层由函数y=4sin(x×π/10+π/2)确定,波纹板四周由宽度为35 mm的刚体提供约束,刚体和前后面板之间设置接触,摩擦系数设置为0.17,面板和芯层相连处采用共节点算法。炸药位于面板中心正上方10 cm处,爆炸载荷的有效作用面积为250 mm×250 mm.面板和芯层均采用边长为1 mm的四节点壳单元。本文主要研究结构几何参数及材料参数对结构响应的影响,因此计算中仅考虑炸药量为12 g的情况。在计算中采用了映射技术[12],首先计算一维冲击波的起爆时间和传播速度,在冲击波将要遇到波纹板时停止计算,将一维的计算结果映射到三维模型中继续计算。当前面板附近的压力下降到大气压时,删除空气网格继续计算,如图3所示。
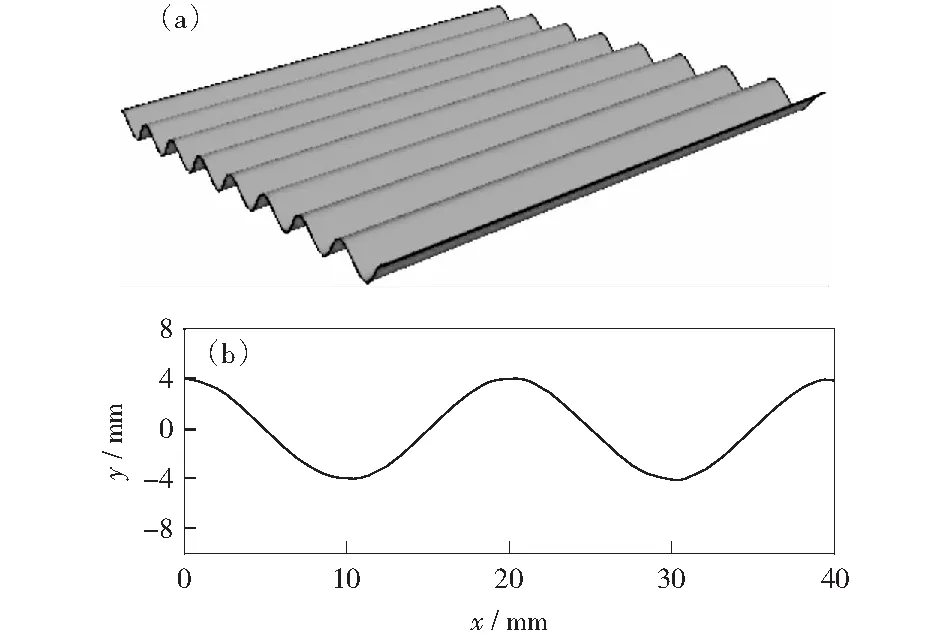
图1 芯层示意图及其波纹函数曲线Fig.1 Core sketch and its wave function
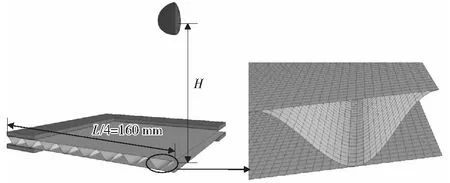
图2 计算模型及网格Fig.2 Quarter-model of corrugated sandwich panel and the core mesh

图3 1维冲击波映射到3维计算模型Fig.3 Blast wave remapped from 1D to 3D model
2 计算结果分析
2.1 动力响应过程
图4中给出了面板厚度为0.8 mm,芯层壁厚为0.2 mm时,夹芯板不同时刻的变形模式。图5给出了夹芯板前后面板的最终变形模态。

图4 不同时刻夹芯板的变形过程Fig.4 Deformation course of sandwich panel in different times interval
从图4中可以看到,夹芯板的动力响应大致可以分为冲击波与前面板的作用阶段、芯层的压缩阶段和夹芯板的整体动力响应等3个阶段。当爆炸载荷作用在前面板之后,芯层中心靠近前面板的部分开始出现屈曲,并且随着载荷的作用不断变形最终压实,中心部分芯层压实之后,夹芯板开始出现整体变形并且芯层从中心向边界处不断压缩。当后面板达到最大位移之后,芯层停止压缩,板开始在平衡位置附近做小幅自由振动,并随着能量的耗散最终停止运动。同时从图5中可以观察到,在面板平行于波纹方向的边界处出现了褶皱。从芯层的拓扑构型可以知道,在垂直于波纹的方向上其抗弯能力将明显大于沿着波纹的方向,因此在沿着波纹方向的边界处首先出现褶皱现象。

图5 前后面板最终变形模态Fig.5 Final deformation of before and back face sheets
在计算过程中选取了10个测量点记录夹芯板前后面板不同位置的速度、应变时程、具体测量点位置如图6所示。

图6 测量点位置Fig.6 Gauge points positions
图7中给出了夹芯板前后面板中心的速度时程曲线。从图中可以看到,炸药起爆之后,前面板获得加速度,同时芯层开始不断压缩,当芯层压实之后前后面板获得共同速度,夹芯板开始整体的变形过程。QIU et al[3]将夹芯板的动力响应解耦为3个阶段:第一阶段,仅前面板获得动能;第二阶段,芯层的压缩阶段;第三阶段,夹芯板的整体动力响应阶段。但从速度时程曲线可以看出,在前面板获得动能的同时后面板也开始缓慢地加速,并且在芯层压缩的过程中后面板的速度也不断增大,最终和前面板达到共同速度。结合图4中的动力响应过程可以看到,3个阶段在响应过程中相互耦合,因此QIU et al的3阶段模型在分析夹芯板的动力响应时相对保守。
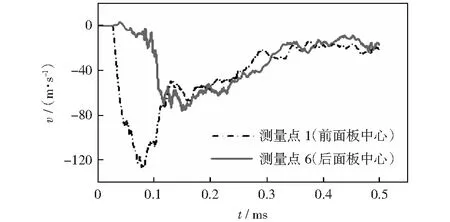
图7 前后面板中心速度时程曲线Fig.7 Velocity history of face sheet centre
图8中给出了测量点1-10的面内应变时程曲线。从图中可以看出,夹芯前后面板在5和10位置点出现了明显的向面板对称边界褶皱的现象,因此这两点的应变均较大且属于压缩应变;而在前面板的其余各点均为正应变,其值由中心向边界处不断减小;在后面板上沿着波纹方向各测量点的应变值同样是从中心向边界处不断减小;但在垂直于波纹方向的位置点9的曲线可以看到,其应变值首先出现为负,然后才变为正值。也就是说,首先出现由于弯曲而产生的压缩变形,随后在面板整体运动的过程中又变为拉伸变形,这一现象同样是由于沿波纹方向的弯曲刚度较小所造成的。对比前后面板的应变可以发现,由于前面板的变形大于后面板,因此在相同位置时,前面板的应变值也大于后面板。

图8 1-10测量点的面内总应变时程曲线Fig.8 Curves of total in-plane strain-time at the gauge points 1-10
2.2 参数分析
在模拟计算中,以面板厚度为0.8 mm,芯层壁厚为0.2 mm,面板和芯层屈服强度为130 MPa为基准,分别考虑面板厚度、芯层壁厚、面板屈服强度及芯层屈服强度等4个参数对结构响应的影响。
图9中给出了不同参数下后面板中心的最大挠度变化。从图中可知,随着芯层壁厚、屈服强度及面板厚度、屈服强度的增加,后面板中心的最大挠度均不断减小。也就是说,随着这些参数的增大,夹芯板的整体抗冲击性能有所提高,并且在这4个参数中,面板和芯层的厚度对挠度变化的影响最大。

图9 不同厚度和屈服强度下后面板中心最大挠度Fig.9 Maximum deflection of back face sheet under different thick and yield stress
图10和图11中给出了不同芯层面板厚度和屈服强度下夹芯板的总吸收能量及前后面板和芯层的能量吸收比例。从图中可以看到,随着这4个参数的增大,夹芯板所吸收的能量都在逐渐减小,并且芯层能量的吸收比例远大于前后面板,也就是说在能量吸收方面芯层占主导地位。
1) 芯层壁厚与屈服强度对能量吸收比例的影响。从图10(a)和图11(a)中可以看出,随着芯层壁厚和屈服强度的增加,前面板的能量吸收比例也随之增加,芯层吸收的能量比例先增大后减小,后面板能量吸收比例先减小后增大。当芯层较薄且屈服强度较低时,载荷作用下芯层将迅速被压实,芯层所吸收的能量迅速饱和,后面板将在载荷作用下产生较大的塑性变形;而随着芯层壁厚和屈服强度的增加,芯层能量吸收的能力相应增加,因此其能量吸收所占比例也相应增加,后面板的塑性变形不断减小,其最终位移也相应减小;而当芯层壁厚大于0.3 mm,屈服强度超过180 MPa之后,由于芯层抵抗塑性变形的能力有较大提高,在载荷条件相同时,其能量吸收将逐渐减小,因此前后面板的所吸收的能量比例也将相应的增加。
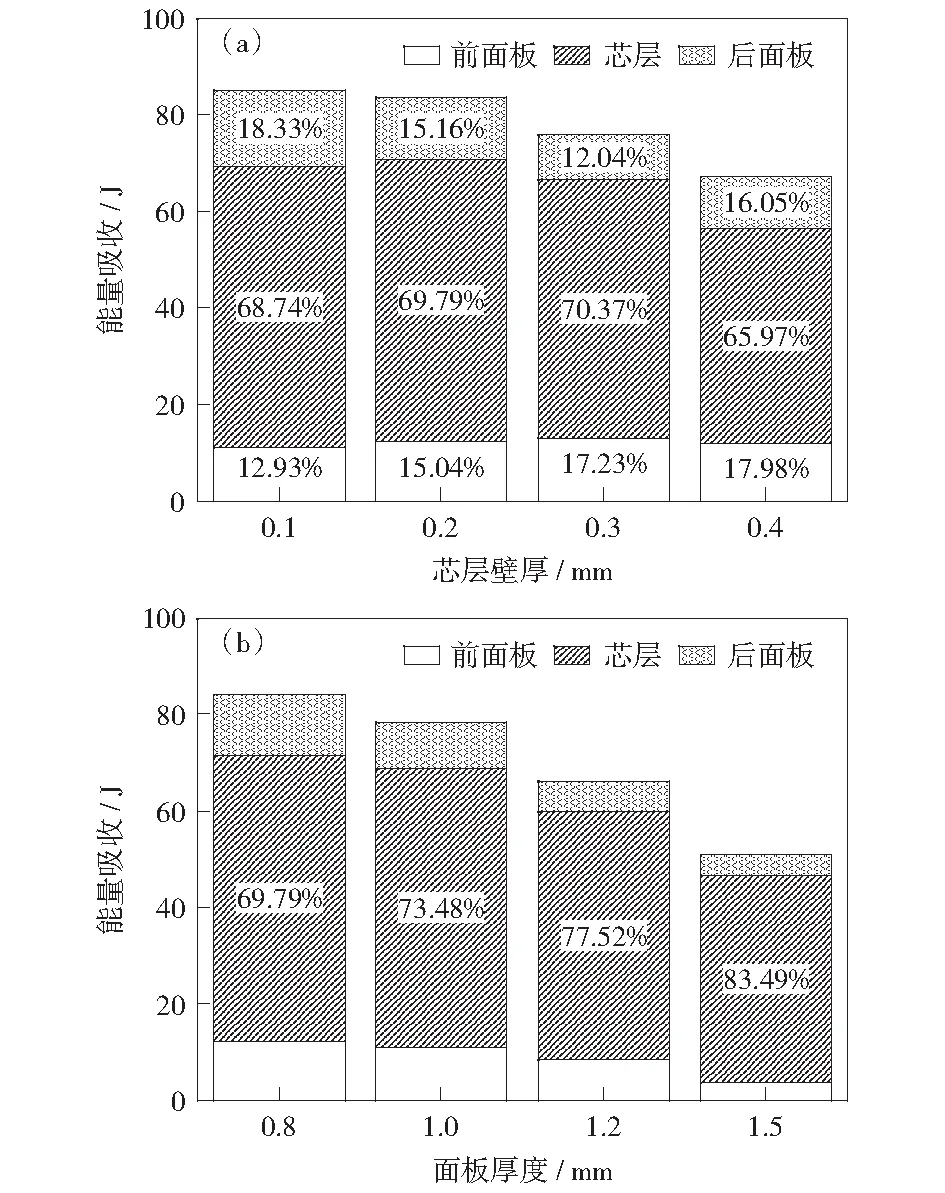
图10 不同厚度下前后面板及芯层能量吸收比例Fig.10 Energy absorption of face sheets and core under different thicknesses
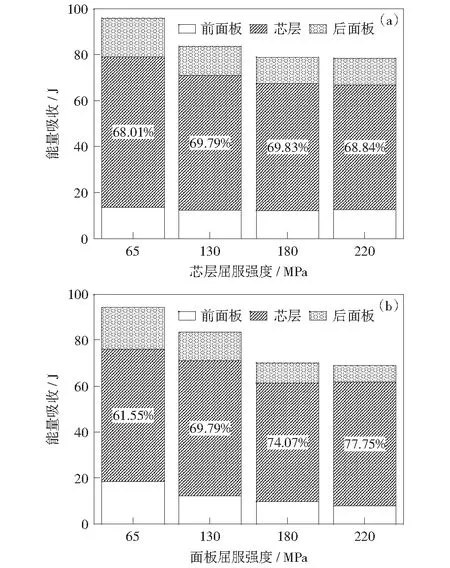
图11 不同屈服强度下前后面板及芯层能量吸收比例Fig.11 Energy absorption of face sheets and core under different yield stresses
2) 面板厚度与屈服强度对能量吸收比例的影响。从图10(b)和图11(b)中可以看出,随着面板厚度和屈服强度的增大,芯层所吸收的能量比例也逐渐增大,前后面板的能量吸收比例逐渐减小。随着面板厚度和屈服强度的增大,当载荷条件一定时,其塑性功消耗随之减小,因此芯层所吸收的能量比例也将随之增大。
同时对比这4个参数可以发现,在能量吸收方面,面板厚度及屈服强度在对能量吸收的影响方面影响最大。
从以上分析可知,在波纹板的抗爆设计中,需要根据具体的服役环境,对芯层、面板的厚度及屈服强度进行合理的设计,使夹芯结构既经济又能满足服役环境。
3 结论
通过采用AUTODYN对爆炸载荷作用下波纹夹芯板的动力响应进行了数值模拟,分析了面板、芯层的参数对结构动力响应的影响。主要结论有以下:
1) 波纹夹芯板在爆炸载荷作用下的动力响应可以分为冲击波的作用阶段、芯层压缩阶段和整体动力响应阶段,并且3个阶段在动力响应过程中相互耦合。
2) 爆炸载荷作用下芯层将从靠近前面板附近首先屈曲并逐步压实;由于波纹芯层在垂直于波纹的方向上其抗弯刚度较大,载荷作用下在平行于波纹的边界处更容易出现褶皱现象。
3) 随着面板、芯层的厚度和屈服强度的提高,夹芯板的整体能量吸收及后面板的最终挠度均逐渐减小。
[1] 王志华,朱峰,赵隆茂.多孔金属夹芯结构动力学行为及其应用[M].北京:兵器工业出版社,2010.
[2] GIBSON L J,ASHBY M F,CELLULAR S.Structure and Properties:2nd ed[M].UK:Cambridge University Press,1997.
[3] QIU X,DESHPANDE V S,FLECK N A.Dynamic response of a clamped circular sandwich plate subject to shock loading[J].J Applied Mechanics,2004,71(5):637-645.
[4] XUE Z,HUTCHINSON J W.Preliminary assessments of sandwich plates subject to blast loads[J].Int J Mech Sci,2003,45(4):687-705.
[5] CUI X,ZHAO L M,WANG Z H,et al.Dynamic response of metallic lattice sandwich structures to impulsive loading[J].Int J Impact Eng,2012,43:1-5.
[6] ZHU F,ZHAO L,LU G,et al.Deformation and failure of blast loaded metallic sandwich panels——experimental investigations[J].Int J Impact Eng,2008,35(8):937-951.
[7] LI X,WANG Z H,ZHU F,et al.Response of aluminium corrugated sandwich panels under air blast loadings:experiment and numerical simulation[J].Int J Impact Eng,2014,65:79-88.
[8] LI X,ZHANG P,WANG Z H,et al.Dynamic behavior of aluminum honeycomb sandwich panels under air blast:Experiment and numerical analysis[J].Compos Struct,2014,108:1001-1008.
[9] LI X,LI S Q,WANG Z H,et al.Response of aluminum corrugated sandwich panels under foam projectile impact——experiment and numerical simulation[J].J Sandw Struct Mater,2016,19(5):595-615.
[10] HUANG W,ZHANG W,HUANG X,et al.Dynamic response of aluminum corrugated sandwich subjected to underwater impulsive loading:experiment and numerical modeling[J].Int J Impact Eng,2017,109:78-91.
[11] ZHANG P,CHENG Y,LIU J,et al.Experimental study on the dynamic response of foam-filled corrugated core sandwich panels subjected to air blast loading[J].Composites Part B Engineering,2016,105:67-81.
[12] Century Dynamics Inc.AUTODYN:remapping tutorial[M].Houston:Century Dynamics,2005.

