非线性边界条件下具非线性耗散粘弹性梁方程的整体解

薛亚荣，张建文

(太原理工大学 数学学院，太原 030024)

1 引言

张建国等[1]研究了一类轴向载荷和横向载荷作用下具非线性耗散项粘弹性简支梁方程

的解的存在唯一性和渐近性，其中A为Laplace算子-Δ.

张建文等[2-3]研究了一类轴向载荷和横向载荷作用下的非线性粘弹性梁方程

解的存在唯一性。

王旦霞等[4]研究了上述系统在非线性边界条件下

整体解的存在唯一性。

在前人的基础上，将研究非线性边界条件下梁方程的整体解。笔者将研究梁受轴向载荷和横向载荷的作用且又受到非线性外阻尼的作用[5]，证明了如下梁方程

(1)

满足初始条件

w(x,0)=w0(x),wt(x,0)=w1(x) .

(2)

及非线性边界条件

w(0,t)=w(2)(0,t)=w(1)(l,t)=0 ,

(3)

(4)

2 定义及假设

定义1 记Ω=(0,l)，定义Sobolev空间：V={u∈H2(Ω)|u(0,t)=u(1)(l,t)=0}，其范数为‖w‖v=‖w(2)‖2；定义Sobolev空间：W={u∈V∩H4(Ω)|u(2)(0,t)=0}，其范数为：‖w‖W=‖w(2)‖2+‖w(4)‖2.

假设1 函数M(·),N(·)满足M(0)=0,|M'(x)|≤c,N(0)=0,|N'(x)|≤c和N(s)s≥0.

3 主要结果

4 定理的证明

考虑系统(1)—(4)的变形问题，即求u∈W，对一切w∈V有

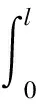
(5)

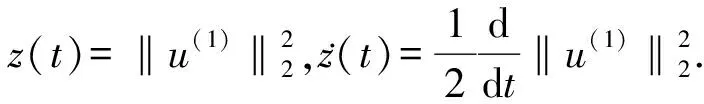
Step 1：取W中一组标准正交基{wj(x)}，简记为{wj}，并有{u0,u1}∈span{w1,w2},对于任何固定的正整数m,假设w1,w2,…,wn,…是W的规范正交基，故Wm=span(w1,w2,…,wm)，构成近似解

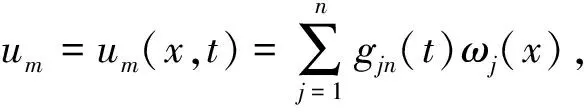
使得对Wm中的任意w,um(t)满足逼近方程

(6)

和初始条件

(7)

Step 2：给出解um的先验估计，以使解拓广到对一切t>0有定义。

估计2 在式(6)中取w=üm(x,t)及t=0，再利用分部积分法及相容性条件得

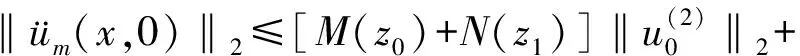
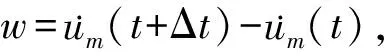
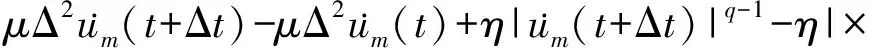
(üm(t+Δt)-üm(t)+Δ2um(t+Δt)-Δ2um(t)+f(um(l,t+Δt))) .

即

因此，可得

(8)

令

Φm(t)=|u'm(t+Δt)-u'm(t)|2+Δ2|um(t+Δt)-um(t)|2.

(9)

注意到式(8)，式(9)变为

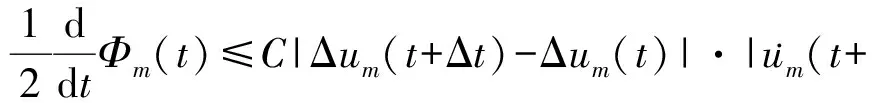
(10)

式中，C为不同常数，由zm(t)的定义及已得的有界性结论，可得

代入式(10)右端第2项，用Young不等式，得

Φ'm(t)≤CΦm(t)+|f(t+Δt)-f(t)|2.

利用Gronwall不等式，对于∀t∈[0,T]，有

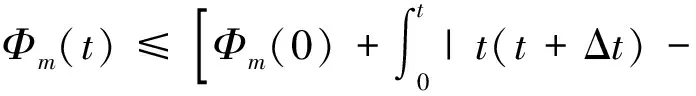
(11)

上式两端同除以(Δt)2，令Δt→0，对一切m，∀t∈[0,T],得

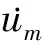
于是，在L2(0,∞;V)中，

弱星收敛于Ψ.

(12)

Step 4：证明u是式(1)和式(2)的解。

对于每个固定的j，有：

所以式(4)成立。

对于∀w∈L2(0,∞;V),有

(13)

当m→∞时，式(13)右端第1项和第2项都趋于0，

此时，式(13)中第3项变为

(14)

因为{um}在L2(0,∞;V)中有界，V⊂H是紧嵌入，所以在L2(0,∞;V)中，{um}强收敛于u.因此对任意w∈L2(0,∞;V)，当时m→∞，有

Step 5：证明解的唯一性。

设u和v是式(1)、式(2)的两个解。记

令w=u-v,则

所以

(15)

故|zu(t)-zv(t)|≤(|u|+|v|)·|Δw| .

(16)

(17)

将式(16)、式(17)代入上式，利用Young不等式，得

唯一性得证。

[1] 张建国,张建文.具非线性耗散粘弹性梁方程的整体解[J].工程数学学报,2001,18(2):61-68.

ZHANG J G,ZHANG J W.The global solutions for the equations of nonlinear viscosity-elasticity beam[J].Chinese Journal of Engineering Mathematics,2001,18(2):61-68.

[2] 张建文,张建国,李庆士.具强阻尼非线性粘弹性梁方程的整体解[J].工程数学学报,2003,20(2):30-34.

ZHANG J W,ZHANG J G,LI Q S.The global solutions for the equations of strongly damped nonlinear viscosity-elasticity beam[J].Chinese Journal of Engineering Mathematics,2003,20(2):30-34.

[3] 张建文,李庆士,蔡中民.具强迫项非线性梁方程解的渐近性[J].应用数学,2001,14(1):60-66.

ZHANG J W,LI Q S,CAI Z M.The Asymptotic behavior of solutions for the equations of nonlinear beam with distributed load[J].Mathematica Applicata,2001,14(1):60-66.

[4] 王旦霞,张建文,王银珠.非线性边界条件下粘弹性梁方程的整体解[J].中北大学学报(自然科学版),2006,27(2)128-131.

WANG D X,ZHANG J W,WANG Y Z.Global solutions to elastic beam equations under nonlinear boundary conditions[J].Journal of North University of China(Natural Science Edition),2006,27(2):128-131.

[5] BALL J M.Initial-boundary value problems for an extensible beam[J].J Math Anal,1973,42:61-68.

[7] BALL J M.Stability theory for an extensible beam[J].J Differ Equa,1973,14(3):399-418.

[6] MA T F.Boundary stabilization for a non-linear beam on elastic bearings[J].Math Appl Sci,2001,24(8):583-594.