基于指数平滑法与回归分析相结合的GDP预测

王红超，王红蕾

（1.贵州大学管理学院，贵阳 550025；2.贵州大学，贵阳 550025）

引言

国内生产总值（GDP）反映了一个国家的经济发展水平与综合国力。因此，国内外对GDP的研究也越来越重视。在进行GDP预测时，国内外采用的方法主要有：时间序列分析模型[1～4]、灰色模型（GM）[5]、混频数据回归模型（Mixed Date Sampling，MIDAS）[6]、神经网络模型[7～10]、插值函数预测法[11]、组合方法[12～15]等，但以上方法大多都只是采用单一方法进行GDP预测，都没有涉及指数平滑法和回归分析两种方法的有机结合。所以，本文采用这两种方法对2017年我国的GDP进行了预测，最终选取二者的算术平均值作为预测结果，以此达到减少误差的目的。

指数平滑法作为加权平均法的一种特殊形式，在进行预测时，无须对复杂系统内部因素与内在联系进行定量研究，而是从数据本身观测有价值的信息。指数平滑法克服了移动平均法的缺点，减少了由于间隔期数N以及权重选取的主观因素产生的误差[16]。回归分析是在相关分析的基础之上发展起来的，它能够准确地计算出每个因素之间的关系以及回归拟合度的变化情况，提高预测的精度。回归分析在进行多种因素分析时，计算简便而快捷。但是，两种方法的缺点是，只能用于短中期预测，对于长期预测时精度不高。

本文根据《国家统计年鉴》所给出2006—2015年的时间序列，采用二次指数平滑法与回归分析相结合的方法，对我国2017年的GDP进行预测，具体（如表1和下页图1所示）。

表1　2006—2015年GDP统计表

一、建立指数平滑法与回归分析模型

指数平滑法曾被很多学者叫作指数加权平均法，该方法是美国学者Robert G.Brown在1959年首次提出的，他论证了时间序列的总体趋势会呈现鲁棒性和规范性，能够科学合理地进行预测。通过该方法的运用，以及在此基础上的详细分析，能够准确揭示出数据的变化规律，它弥补了移动平均法进行预测时的缺点。总之，采用指数平滑法，思路清晰、计算简便、易于理解，如今计算软件的运用能够快速得出计算结果，节省了很多时间，因而在实际的预测过程中备受广大学者的青睐。正因为如此，它的应用横跨了包括工业、农业、商业等众多领域。而指数平滑法也包含一次、二次、三次指数平滑法，在进行预测时到底如何选择，还要根据相关的数据信息，即通过分析时间序列的走势来决定。

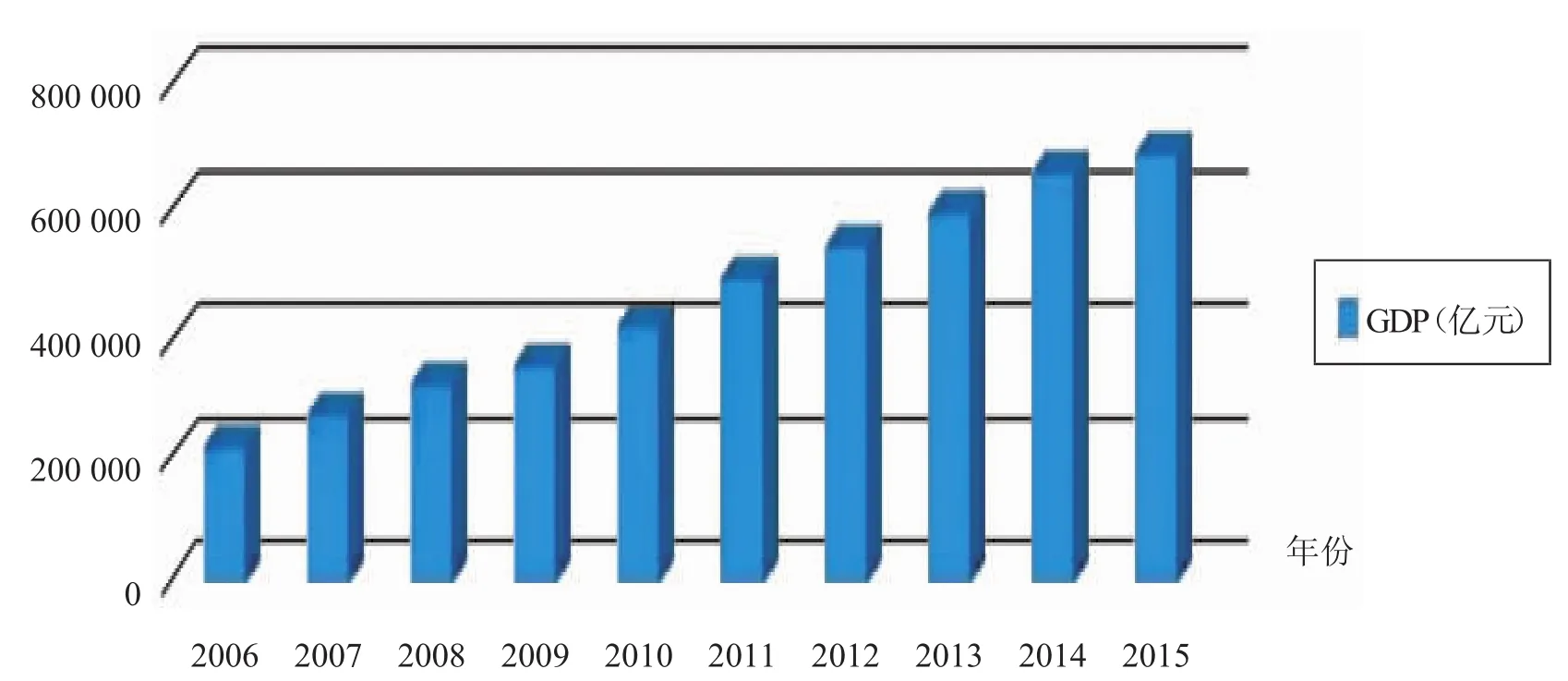
图1　2006—2015年GDP趋势图

回归分析又称为曲线拟合，它是对已知的样本数据进行分析，从而确定各变量之间的关系，构建函数表达式，然后进行短中长期预测。回归分析有线性回归与非线性回归两类，而线性回归又分为一元线性回归与多元线性回归。本文根据GDP的线性趋势，选用一元线性回归预测方法。

（一）一次指数平滑法

一次指数平滑法在时间序列分析中，多用于比较简单、数据信息较为平稳的预测，假定 Y1，Y2，……，Yn，为时间序列，那么，一次指数平滑法的公式可表示为：

式中，S1t为时间t的预测值；Yt为时间t的实际值，St-1为时间t-1的预测值，a为平滑常数，取值范围0～1。当a取1时，St=Yt；当a=0时，St=St-1。预测值具有不断递推性质，因此可递推至S1，涵盖了之前的全部观测值。在递推过程中，平滑常数a是根据指数形式逐步递减的，因此称其为指数平滑法。

（二）二次指数平滑法

所谓二次指数平滑法，其实就是在第一次指数平滑结果上再做一次指数平滑预测，这种方法应用于当预测的数据服从线性分布时，即时间序列数据表现为线性趋势时。二次指数平滑法的公式为：

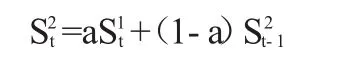
预测公式可转化为：

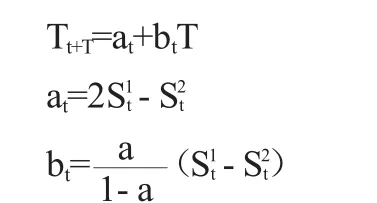
（三）一元线性回归

一元线性回归（linear regression）只针对1个自变量引起1个因变量发生变化进行的研究。一元线性回归方程为：

yˆ=b0+b1x

式中，b0是直线在y轴上的截距，而b1为直线的斜率，它表示变量x在变动每1个单位时，y的平均变动值。b0和b1两个参数是运用最小二乘法求得的，其最终表达式为：

二、指数平滑法中初始平滑值与平滑常数a的选择

在对时间序列以往近期数据进行预测时，常用来确定指数平滑法初始平滑值的方法有两种：=Y1，一般都采用这种方法；而另一种就是

运用指数平滑法时，如何确定平滑常数a尤为重要，因为平滑常数的取值情况代表了每个时期的实际值以及预测值占据的比重。实际值和预测值的比重之和应为1，即平滑常数与阻尼系数之和为1。确定平滑常数的原则就是如何使实际值与预测值之间的误差实现最小化[17]。

通常采用最小均方差的方法确定平滑常数，因为a的取值为0～1这个区间，所以可以选择不同的a值，代入进行计算，最后选取最小的均方差所对应的a值为最优的平滑常数。还可以根据经验代入法进行试算，筛选平均误差百分率最小的a为最终指数平滑常数。特别要注意的是，当采取经验判断法时，如果时间序列趋势较为平稳时，a的取值要在0.05～0.20之间选择，使预测结果更加符合实际；当时间序列存在波动，但就长期来看其变化并不明显，这时a就可以在0.1～0.4之间选取；而当时间序列变化的波动很大时，表现为急剧上升（骤然下降）时，就要考虑选取较大的平滑常数a，在0.6～0.8之间选择；当时间序列呈现下降（上升）的发展趋势时，a的取值可在0.6～1中选择。

三、算例——国内生产总值（GDP）预测

为了验证指数平滑法和回归分析法在预测GDP中的应用，本文选取《国家统计年鉴》发布的截至2015年的国内生产总值为时间序列数据，分别采用了二次指数平滑法及一元线性回归法进行了预测，最终选取二者的算术平均值为最终的预测结果。计算结果充分说明了采用指数平滑法与回归分析的有机结合对GDP预测的有效性和科学性。

表2　不同α值计算所得的时间序列预测值

表3　α=0.95时二次指数平滑计算值

续表

图2　一次指数平滑折线图

图3　二次指数平滑折线图

由表2可知，当a=0.95时，平均误差百分率为0.6%，时间序列预测结果可以满足精度的要求。按照二次指数平滑法的预测模型Yt+T=at+btT得：Y2015+T=689 062.72+45 477.59T。要预测2017年我国的GDP，代入T=2即可，则：Y2017=689 062.72+45477.59×2=780 017.90。根据二次指数平滑折线图趋势推测可知，2017年的预测结果可能会略低于时间序列实际值。

下面介绍用一元线性回归来进行我国2016年国内生产总值（GDP）的预测。通过Excel计算结果（如表4所示），残差图和线性拟合图（见下页图4和本文图5）。

根据一元线性回归方程Y=b0+b1x，由计算结果代入得：Y=157 207.4+53 766.6×12=802 406.6亿元。

最后，求取二次指数平滑的算术平均值作为2017年最终的预测结果，即 1/2（Y2017+Y）=1/2（780 017.9+802 406.6）=791 212.25亿元。两种方法的预测值相比实际值都略微偏低，所以最终的结果可能会比2017年的实际GDP偏低，但既然是预测，误差在所难免。只要微小的误差在允许范围之内，那么预测结果就有其参考价值与合理性。

表4　算例计算结果

续表 方差分析

RESIDUALOUTPUT　PROBABILLTYOUTPUT

图4　残差图

图5　线性拟合图

通过以上两种预测方法可知，未来的几年，我国的国内生产总值（GDP）会持续增长，因为我国正处于高速发展时期，市场中的经营主体积极响应国家号召——实现中国梦，积极投身于经济建设之中，为中国经济的快速持续发展迎来春天。

结语

本文根据《国家统计年鉴》至2015年的国内生产总值（GDP），采用二次指数平滑法和一元线性回归相结合的方法，对2017年我国的国内生产总值（GDP）进行了预测，通过两种方法的计算结果，表明该方法在进行短期GDP预测时较为合理，精度相对较高，有一定的科学性。由此而得到的时间序列预测的结果，可以用来作为相关部门对短期GDP预测的参考点，以便对经济政策做出适时的调整。虽然两种方法预测优势明显，但是也存在着一定的缺点，它们只适合短中期的预测，对于长期预测就有一定的局限性。因为GDP的波动影响因素众多，随着时间的推移，各种可变因素可能随时发生变化，导致骤然上升或急剧下降，最终导致两种预测方法失稳，从而达不到短期预测的目的。针对长期预测，还要根据各种可变因素进行不断修正，才会得到较为科学合理的结果。

参考文献：

[1]郝香芝，李少颖.我国GDP时间序列的模型建立与预测[J].理论新探，2007，(23)：4-5.

[2]魏宁.时间序列分析方法研究及其在陕西省GDP预测中的应用[D].杨凌：西北农林科技大学，2010.

[3]李守丽.时间序列模型在地级市GDP预测中的应用[D].郑州：郑州大学，2013.

[4]张江城.基于时间序列的我国GDP的短期预测[J].商，2016，(15)：204-206.

[5]李生彪.基于改进的灰色马尔可夫链方法的甘肃省人均GDP预测[J].甘肃科技，2013，(1)：1-3.

[6]王维国.基于混频回归类模型对中国季度GDP的预报方法研究[J].数量经济技术经济研究，2014，(4)：108-125.

[7]郭秋艳.基于DFA方法和BP神经网络的GDP预测模型[J].统计与决策，2014，(8)：82-84.

[8]单玉隆.ARIMA模型与遗传算法优化神经网络在GDP预测中的应用[D].兰州：兰州大学，2014.

[9]蒋雪.基于BP神经网络技术的GDP预测方法[J].经济论坛，2010，(3)：203-204.

[10]杨挺.基于BP神经网络改进算法的湖南省GDP预测研究[D].长沙：中南大学，2008.

[11]洪艳.一种基于插值拟合的GDP预测方法[J].中国管理信息化，2016，(8)：123-124.

[12]苑慧芳.基于AIC的组合预测方法在地区GDP预测中的应用[J].山东理工大学学报：自然科学版，2016，(9)：64-69.

[13]詹英.组合预测方法在我国人均GDP预测中的应用[D].武汉：华中师范大学，2014.

[14]陈邦锐.组合预测方法在江苏省GDP预测中的应用[J].科技创新导报，2012，(25)：105-106.

[15]肖智.基于PSO_PLS的组合预测方法在GDP预测中的应用[J].管理科学，2008，(6)：115-121.

[16]徐建新，严勇，严富海.指数平滑法在典型城市GDP预测中的应用[J].水利科技与经济，2008，(7)：551-554.

[17]张德南，张心艳.指数平滑预测法中平滑系数的确定[J].大连铁道学院学报，2004，(3)：79-80.