利用反作用飞轮抑制太阳电池阵振动的原理和方法研究

陈必发，吕亮亮，彭福军，唐国安

(1. 复旦大学 航空航天系，上海 200433；2.上海市空间结构机构重点实验室/上海宇航系统工程研究所，上海 201109)

0 引言

各种天线、太阳帆板、大型桁架结构等柔性附件相对于航天器本体具有尺寸大、固有频率低等特点，姿态调整、变轨机动等在轨操作很容易引起柔性附件的大幅振动。在太空运行环境中，柔性附件的振动一旦被激起，其衰减过程将相当缓慢，不仅影响航天器正常的任务执行，还会一定程度影响航天器的结构强度和使用寿命。降低柔性附件的振动至少可从两方面入手。一方面是减小航天器调姿或变轨对柔性附件的激励，例如文献[1-4]中将零位移输入整形技术应用于太阳阵调姿，利用驱动机构现有的硬件，无须增加其他附件，即可将初始参考指令与一系列脉冲序列卷积生成整形指令作为输入信号，较好地抑制了残余振动。另一方面是利用主动或被动控制技术抑制激励结束后柔性附件的自由振动，加快振动的衰减。

航天器柔性附件的振动控制方法可分为被动控制、主动控制以及半主动控制。常用的被动控制方法有黏弹性材料制成的黏弹性阻尼器[5]、压电分流阻尼系统[6]等。主动控制常用的执行机构包括反作用推力器[7]、压电材料[8]等。而半主动控制意图结合主动控制和被动控制两种方法的优点，如基于同步开关阻尼技术，利用压电叠堆振动控制天线展开臂[9]。

主动控制方法因适应性强、控制效果好等优点备受学者们关注[10-13]。文献[8]中研究了压电纤维复合材料(MFC)，将其应用于可展开、可固化桁架结构的振动状态控制中，取得了令人满意的效果。文献[14]中提出在电池阵结构中引入压电材料，分别利用速度反馈、线性二次最优调节器(LQR)设计控制系统，通过数值仿真证明二者均能有效抑制振动。但以压电材料为传感/作动器的控制方法相对于大型柔性附件的振动，作用范围较小，例如美国AstroMesh天线的展开口径达25 m[15]，即便是微小的干扰也会导致结构某些部位产生大幅值响应，控制效果易受限。由此，如何提高以大型柔性附件为控制对象的减振效率是一个亟待解决的问题。文献[16]中以大型线性桁架结构为控制对象、以开关式喷气推进器和压电材料为作动器，通过实验证明并用两种控制方法可在提高振动衰减效率的同时减少推进器的工质消耗。但工质消耗问题仍不利于其频繁采用。

反作用飞轮(以下简称飞轮) 常被用于卫星的姿态控制，具有质量轻、尺寸小、效率高等诸多优点[17-18]。若在柔性附件上安装飞轮，根据一定的控制律调节飞轮的旋转角速度，对柔性附件施加因飞轮变速产生的反作用力矩，利用扭矩做功消耗结构的振动机械能，使结构更快地恢复到平衡状态，实现抑制柔性附件振动的目的。本文将研究振动抑制的原理、实现及仿真结果。

1 振动抑制的过程和原理

以航天器太阳能电池阵为对象，研究其受激励后的振动抑制问题。在航天器本体惯量远大于电池阵惯量的情况下，电池阵可视为根部固支的弹性结构。如图1所示[19-20]，以CARTOSAT对地观测卫星为例，建立以电池阵根部为原点、展开方向为X轴、垂直于阵面方向为Z轴的直角坐标系O-XYZ。当航天器发生Z向变轨或其他形式的机动时，电池阵受到扰动后产生振动。这种振动主要以垂直于阵面、即XZ平面内的横向弯曲振动为主。为加速振动的衰减，可考虑在电池阵的适当位置安装飞轮(如图1所示)。飞轮转速Ω的变化会产生施加到电池阵的扭矩T，扭矩做功将消耗电池阵振动的机械能。

图1 电池阵振动问题分析的参考坐标系Fig.1 Reference coordinate system for analysis of vibration of solar array

若飞轮转动部分的转动惯量为I，则扭矩可表示为

(1)

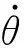
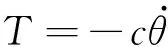
(2)

式中：c为比例系数。飞轮的作用相当于对电池阵添加人工阻尼，系数c故称为人工阻尼系数。将式(2)代入式(1)，并对时间积分后可得

Ω=-cθ/Ι

(3)

这是一种线性增益关系，可根据电池阵飞轮所处位置角度θ确定飞轮应有的转速Ω。

从动力学基本方程出发，将描述电池阵振动型态的广义位移向量记为x，飞轮所处位置的角度θ可表示为向量x分量的线性组合

θ=LTx

(4)

当电池阵发生虚位移δx时，飞轮扭矩作的虚功为δW=T(t)δθ=(δx)T(L·T)。故扭矩对于电池阵的广义力为L·T。在此广义力的作用下，电池阵的位移向量x服从运动微分方程

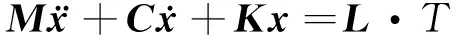
(5)

式中：M、K、C分别为电池阵模型的质量矩阵、刚度矩阵以及阻尼矩阵。

电池阵高阶振动自然衰减较快，振动抑制对象主要以低阶模态为主。若仅考虑一阶弯曲振动，向量x可用电池阵根部固支、XZ平面内的一阶横向弯曲模态φ1表示，即

x=φ1ξ1

(6)

式中：ξ1为相应的模态坐标。根据式(4)，飞轮所处角度θ可用模态坐标表示为

θ=φθξ1

(7)

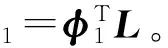
(8)

(9)

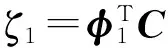
(10)

为由扭矩T产生的人工模态阻尼比。

由式(10)可知，当人工阻尼系数c>0时，总有ζa>0，使得式(9)中的速度项系数满足ζ1+ζa>ζ1，表明飞轮的作用就是增加电池阵的模态阻尼比，从而加快其振动的衰减。这就是利用飞轮抑制电池阵振动的基本原理。

2 控制律设计

由式(3)和式(10)可知，比例系数c越大，减振效果越好，但要求飞轮能提供更大的输出力矩。为此，需在减振效果与飞轮功率之间作适当的权衡。如果知道飞轮在不超载前提下的最大转速是Ωmax，并能估计出振动过程中电池阵飞轮所处位置转角θ的最大值θmax，式(3)中的人工阻尼系数可确定为

(11)

实际情况中，电池阵上飞轮所处位置的转角θ不易直接测得，而电池阵根部的弯矩Mb可通过应变、压电等手段测得。对于线性结构，弯矩Mb可利用胡克定律及几何关系表示为广义位移x的线性函数Mb=(kM)Tx，再利用式(6)又可表示为

Mb=φMξ1

(12)

式中：φM=(kM)Tφ1。联立式(7)和式(12)，消去变量ξ1，又可得转角θ与弯矩Mb的关系

(13)

最终由式(3)，式(11)和式(13)，根据弯矩Mb确定用于抑制电池阵振动的飞轮转速，即

(14)

由式(14)可知，控制系统的输入可利用测量电池阵根部弯矩获得，由此解算飞轮的转速，使得飞轮能输出实现人工阻尼所需要、如式(2)所示的反作用力矩。

3 电池阵有限元模型振动抑制的仿真验证

用飞轮抑制实际尺寸电池阵振动的有效性验证有限元仿真结果，对象是由3块太阳能电池板组成的电池阵，如图2所示。每一块太阳能电池板的长度为170 cm、宽度为320 cm、厚度约为2 cm。连接太阳能电池板的铰链长度为8 cm，整体质量为44.63 kg。建立如第1节所述的直角坐标系O-XYZ，电池阵位于XY平面。

电池板采用壳单元，铰链采用梁单元建模，电池阵根部绕Y轴转动的方向上通过刚度ks=4 500 N·m·rad-1的扭簧连接到航天器本体。在仅考虑电池阵沿Z方向的振动抑制时，根部其余方向位移和转角均假设为刚性连接。电池阵根部的弯矩Mb及其与航天器本体的相对转角θr之间存在如下关系

Mb=ksθr

(15)

电池阵第1阶固有频率为0.21 Hz，对应的是Z方向的弯曲振型，第2阶固有频率为0.87 Hz，对应的是绕X轴的扭转振型。

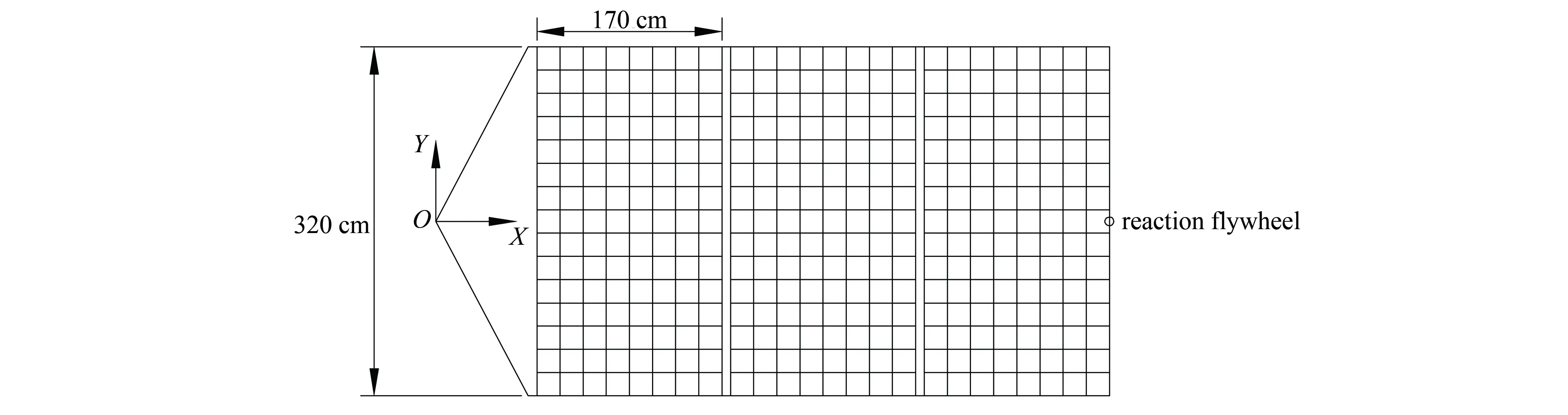
图2 太阳能电池阵有限元模型Fig.2 Finite element model of solar array

为简化计算，电池阵的阻尼矩阵采用比例阻尼形式，即

C=αK+βM

(16)

式中：α=0.018 3;β=0.003 5。即第1阶和第2阶的模态阻尼比均为1%。

电池阵受到的激励来自本体的变轨运动：在0～2 s 时间段，受本体牵连、沿Z轴作匀加速直线运动，加速度为0.1 m/s2；2 s之后作匀速直线运动，速度保持为0.2 m/s。将飞轮安装在电池阵右侧自由边的中点(如图2所示)，对电池阵施加扭矩以期实现对振动的抑制。

根据式(2)、式(13)，飞轮输出的扭矩T可表示为

(17)

式中：kb-T=cφθ/φM的取值越大，电池阵的振动衰减越快，但对飞轮转速、负载能力的要求也相应提高。对于航天应用的产品，飞轮质量也不宜过大。为此可选择质量为1 kg、约占电池阵质量2%的反作用飞轮进行仿真，要求该飞轮的最大输出扭矩不少于为1 N·m。

为利用MSC.Nastran进行仿真，需要将式(17)经拉普拉斯变换到s域上表示

L [T]=-skb-TL [Mb]

(18)

式中：L [·]表示拉普拉斯变换。

弯矩Mb虽是可测量，但由于测量过程中噪声等干扰信号不可避免，通常需对其进行滤波。为更具真实性，仿真时同样也加入滤波环节，滤波器传递函数为Gf(s)。利用式(15)和式(18)，建立经滤波处理后扭矩T与转角θr的关系

L [T]=-kb-TkssGf(s)L [θr]

(19)

常规的滤波器传递函数Gf(s)为有理多项式，MSC.Nastran允许将式(19)表示的扭矩-转角关系以TF(Transfer Function)卡的形式添加到有限元模型中计算动力学响应[21]。

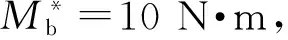
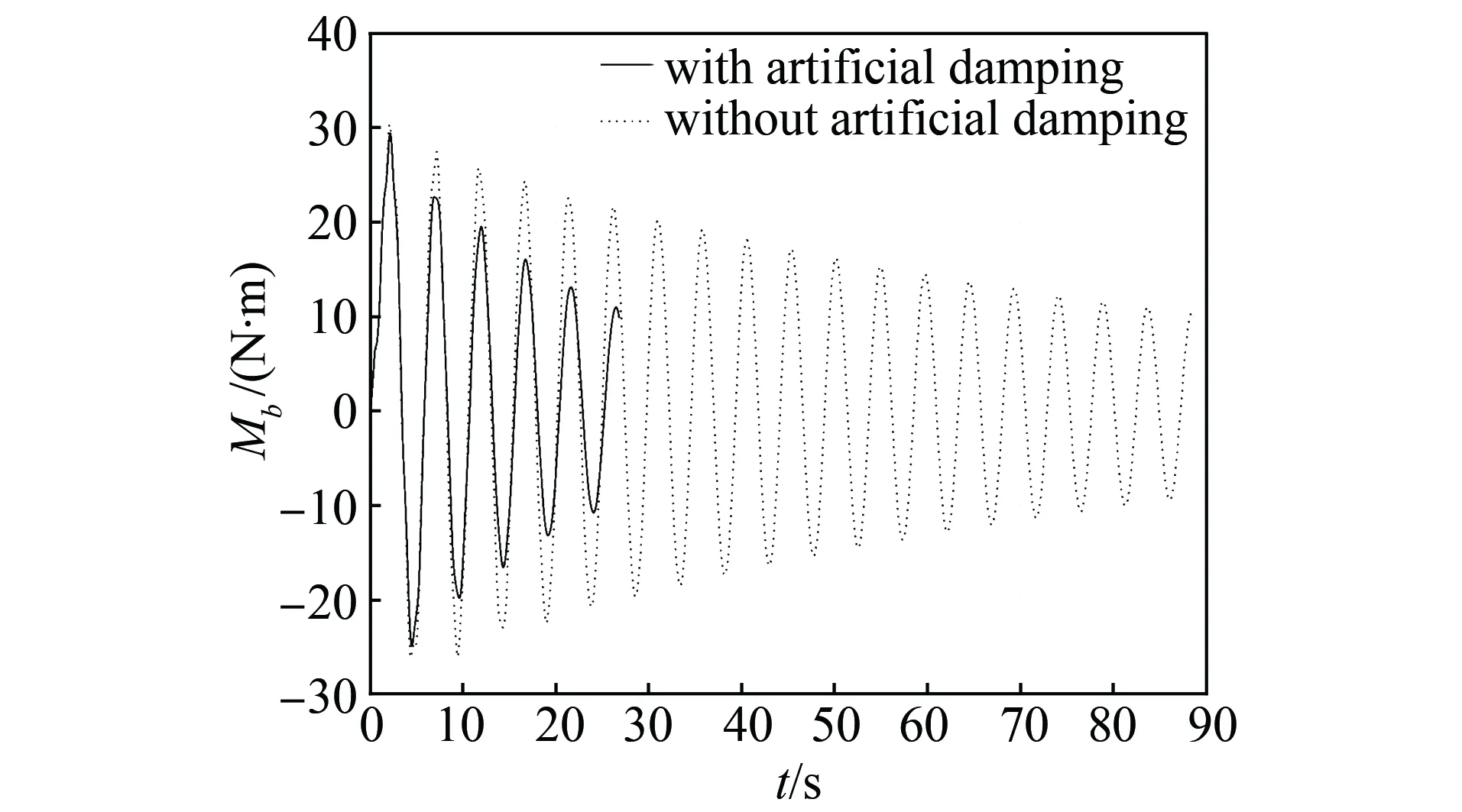
图3 弯矩Mb的衰减历程Fig.3 Attenuation process of bending moment Mb

根据式(10)及系数kb-T的表达式，可知人工模态阻尼比ζa与kb-T的关系为

(20)

图4 飞轮输出扭矩T的变化曲线Fig.4 Varying curve of flywheel output torsional moment

图5 不同kb-T取值对弯矩Mb衰减的影响Fig.5 Influence of different values kb-T on attenuation of bending moment Mb

图6 不同kb-T取值时扭矩T输出的变化(取前30 s)Fig.6 Difference of output torsional moment of flywheel T at different values kb-T (taking the previous 30 s)

为验证人工阻尼系数c或kb-T对振动衰减速度的影响，再取kb-T=1/30 s和1/60 s进行仿真，得到的弯矩响应曲线和飞轮扭矩如图5、6所示。从图5可看出，随着系数kb-T的增大，振动衰减变快。记模态运动方程(9)中的速度项系数ζ1+ζa为施加振动控制后的理论等效阻尼比，其中ζa可根据式(20)得到；同时亦可从弯矩响应曲线图5中提取到kb-T=1/60,1/45,1/30时的仿真等效阻尼比，两者结果如表1所示。

仿真结果与理论结果一致，设计的控制方法达到预计的效果，即随着系数kb-T的增大，等效阻尼比增大。故在飞轮不过载的前提下，应尽量提高kb-T。

表1 不同系数kb-T下的等效阻尼比

4 结束语

本文分别对空间飞行器柔性附件的振动抑制方法作了原理分析和仿真验证。结果表明：这种方法具有清晰的动力学原理，即利用变速飞轮的反作用力矩对结构做负功，消耗其振动的机械能，从而加速振动的衰减。具体工程实现可利用电池阵根部动态载荷(例如电测应变)获得结构的振动响应，解算出飞轮的转速，这使得飞轮能产生实现人工阻尼所需要的反作用力矩。有限元的仿真验证考虑了信号滤波等实际需要，尽可能真实地模拟电池阵的工作状态，结果表明：采用约占电池阵质量2%的飞轮作动器，能使得振动衰减时间缩短2/3，具有较高的效费比。振动抑制就是从测量结构振动应变到输出飞轮驱动信号的线性增益过程。流程简单，对控制器的性能要求较低。

目前的研究工作还局限于单一方向的振动，适合某一类以横向弯曲振动为主要特性的太阳能电池阵。对于其他类型航天器柔性附件的振动抑制还需进一步研究。此外，飞轮提供的反作用力矩和结构应变为增益关系，且增益为一常数。随着应变减小，飞轮实际输出的反作用力矩将小于其额定载荷。因此控制过程中，若能调节增益使飞轮处于满载状态，充分利用飞轮性能，结构将更快地恢复平衡。这也有待进一步研究验证。本方法验证仅实施了仿真部分，实验研究将在今后的工作进行。

[1] NA S, TANG G A, CHEN L F. Vibration reduction of flexible solar array during orbital maneuver[J]. Aircraft Engineering and Aerospace Technology, 2014, 86(2): 155-164.

[2] 那帅, 朱春艳, 彭福军, 等. 基于输入整形技术的太阳翼调姿残余振动抑制实验研究[J]. 振动与冲击, 2013, 32(7): 107-112.

[3] 朱春艳, 绍济明, 唐国安. 双输入整形器抑制两轴转动太阳翼调姿后的残余振动[J]. 噪声与振动控制, 2011, 32(6): 1-4.

[4] 朱春艳, 邵济明, 那帅, 等. 太阳电池翼调姿后残余振动抑制的整形器设计[J]. 振动与冲击, 2012, 31(8): 176-180.

[5] TORISAKA A, YAMAKAWA H. Optimum vibration control design of a light weight structure in wide frequency domain[J]. Journal of Environment and Engineering, 2011, 6(2): 328-339.

[6] SALES T P, RADE D A, DE SOUZA L C G. Passive vibration control of flexible spacecraft using shunted piezoelectric transducers[J]. Aerospace Science and Technology, 2013, 29(1): 403-412.

[7] VELDE W E V, HE J. Design of space structure control systems using on-off thruster[J]. Journal of Guidance, Control, Dynamics, 1983, 6(1): 430-436.

[8] TARAZAGA P, INMAN D, WILKIE W. Control of a space rigidizable-inflatable boom using embedded piezoelectric composite actuators[J]. Journal of Vibration & Control, 2007, 13(7): 935-950.

[9] MAKIHARA K, ONODA J, MINESUHI K. Behavior of piezoelectric transducer on energy-recycling semiactive vibration suppression[J]. AIAA Journal, 2006, 44(2): 411-413.

[10] KALAYCIOGLU S, SILVA D. Minimization of vibration of spacecraft appendages during shape control using smart structures[J]. Journal of Guidance Control & Dynamics, 2015, 23(3): 558-561.

[11] JIANG J P, LI D X. ROBUST H∞vibration control for smart solar array structure[J]. Journal of Vibration and Control, 2010, 17(4): 505-515.

[12] HU Q L. Spacecraft vibration reduction using pulse modulated command input and smart materials[J]. Aircraft Engineering and Aerospace Technology, 2006, 78(5): 378-386.

[13] FAZELZADEH S A, Azadi E. Thermoelastic vibration and maneuver control of smart satellites[J]. Aircraft Engineering and Aerospace Technology, 2017, 89(3): 477-490.

[14] 蒋建平, 李东旭. 智能太阳翼有限元建模与振动控制研究[J]. 动力学与控制学报, 2009(2): 164-170.

[15] THOMSON M W. The Astromesh deployable reflector[C]∥IEEE Antennas and Propagation Society International Symposium. Orlando, FL, 2002: 1516-1519.

[16] LOCATELLI A, SCHIAVONI N, CASELLA F. Modeling and control for vibration suppression in a large flexible structure with jet thrusters and piezoactuators[J]. IEEE Transactions on Control Systems Technology, 2002, 10(4): 589-599.

[17] FONSECA I M D, BAINUM P M, SILVA A R D. Structural control interaction for an LSS attitude control system using thrusters and reaction wheels[J]. Acta Astronautica, 2007, 60(10/11): 865-872.

[18] 龚铁裕. 反作用飞轮控制方案及其稀土永磁电机变结构控制研究[D]. 长沙: 国防科技大学, 2004.

[19] ADDARI D, AGLIETTI G S, REMEDIA M. Experimental and numerical investigation of coupled microvibration dynamics for satellite reaction wheels[J]. Journal of Sound & Vibration, 2017, 386: 225-241.

[20] PETER B. Space recognition guide[M]. 张琪, 付飞, 译. 北京: 人民邮电出版社, 2009: 303.

[21] MSC. Software Corporation. MSC. Nastran version 70: advanced dynamic analysis user′s guide[M]. [S.l.: s.n.], 2002: 25-29.