P92钢在内压和拉伸组合加载下的蠕变行为

， ，，

(华北电力大学电站设备状态监测与控制教育部重点试验室，北京 102206)

0 引 言

我国是世界上拥有超(超)临界机组最多的国家，随着蒸汽温度和压力参数的提高，在机组效率得到提高的同时，也对电站关键部件材料的性能提出了更高要求，尤其是材料的高温强度、抗高温腐蚀和氧化能力等。P92铁素体耐热钢由于具有良好的高温导热性能、高强度和低热膨胀系数等，被广泛应用在我国600/620 ℃等级超超临界机组高温部件中[1]，如高温主蒸汽管道、高温再热蒸汽管道及联箱等。这些部件长期处于高温工作状态，其主要失效形式为蠕变失效，同时在复杂应力和部件几何尺寸的影响下，这些部件大多处于多轴应力状态。通过研究多轴应力状态下P92钢蠕变损伤规律和机理，可以准确评估部件的剩余寿命，对超超临界机组高温关键部件的寿命管理具有重要意义。

国内外学者对多轴应力状态下蠕变的研究主要集中在多轴蠕变试验方法[2]，以及基于连续损伤理论并通过有限元方法模拟材料的力学特性和蠕变损伤特征等方面。一些学者采用缺口试样进行多轴蠕变试验，并研究了其蠕变损伤演变[3-6]，这些研究的试验装置和试样均比较简单，易于操作，但无法实现主应力和静水应力的独立变化，而研究表明利用管状试样可通过不同方式的组合加载来弥补该不足；WANG[7]等利用扭转-压缩-拉伸的加载方式，研究了多轴应力状态下GH33镍基合金的蠕变疲劳交互作用；SELIGER[8]等在研究多轴度对电站管道所用14MoV6-3、10CrMo9-10和X10CrMoVNb9-1耐热钢蠕变行为的影响时，采用了光滑薄壁管和环向缺口薄壁管两种试样，通过控制轴向拉伸应力和管道内压来调整多轴度;YAO等[9]对近年来国内外有关蠕变行为的研究进展进行了综述，通过引入多轴度和参考应力来描述多轴蠕变，根据蠕变过程是由约束孔洞控制还是塑性控制来确定参考应力系数；HYDE[10]等使用Kachanov-Robatnov蠕变模型研究光滑试样和缺口试样的蠕变行为，通过引入不同的等效应力，获得与试验结果一致的模拟结果，但未考虑蠕变第一阶段特性和应力的多轴性。

为研究多轴度对P92钢蠕变行为的影响，作者采用内压和拉伸组合加载的蠕变试验方法，通过控制内压和拉伸载荷获得不同的多轴度，然后在650 ℃下对P92钢管状试样进行了3组不同多轴度的蠕变试验，观察了断口形貌和显微组织，分析多轴应力对P92钢蠕变行为的影响机制；利用能够描述蠕变第一阶段特性的改进的Kachanov-Robatnov蠕变模型对内压和拉伸组合加载下的P92钢蠕变行为进行有限元模拟，并进行试验验证，分析了多轴度对P92钢应力分布和损伤发展的影响。

1 试样制备与试验方法

试验原料为日本JFE钢铁公司生产的ASTM A335 GRADE P92钢，热处理工艺为1 050 ℃保温20 min正火，785 ℃保温60 min回火，化学成分如表1所示。

多轴蠕变试样的形状和尺寸如图1所示：该试样由管上端及封头、中部、下端及封头、填充芯棒等4部分组成；上端与中部、下端与中部均通过焊接方式连接；下端有与内压加载系统连接的通气孔以及与中部连接的导管，试样上下端通过机械螺纹与蠕变试验机连接。

表1 P92钢的化学成分(质量分数)Tab.1 Chemical composition of P92 steel (mass) %

图1 多轴蠕变试样的形状与尺寸Fig.1 Shape and dimension of specimen for multiaxial creep experiment

多轴蠕变试验系统包括压力加载系统和拉力加载系统两个部分，如图2所示。压力加载系统通过增压泵将氮气加压到指定压力后注入试样内部，并保持试验过程中压力波动范围不超过±1%。拉力加载系统由力学加载部分和加热炉部分组成，试验过程中拉力波动范围不超过±1%，试样中部的温度变化范围不超过±3 ℃。试验过程中采用引伸计测得试样轴向方向的变形情况。

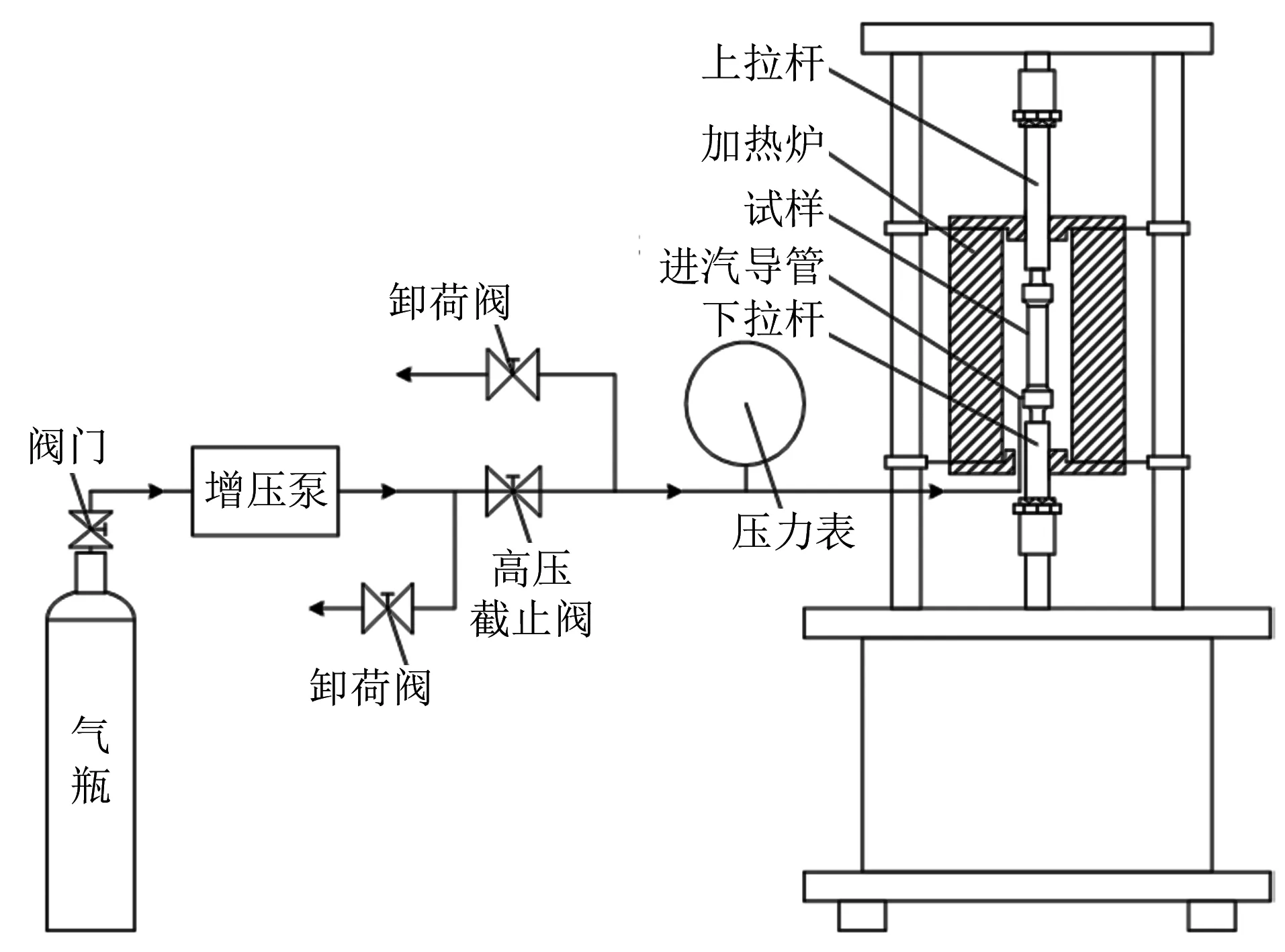
图2 内压和拉伸组合加载的多轴蠕变试验系统示意Fig.2 Schematic of multiaxial creep experiment system under combination loading of inner pressure and tensile

材料的应力状态可以用多轴度来衡量，多轴度是一个无量纲量，一般定义为静水应力与等效应力之比[11]。为研究多轴应力对P92钢蠕变行为的影响，作者选取如表2所示的3组载荷组合，在650 ℃下进行多轴蠕变试验。

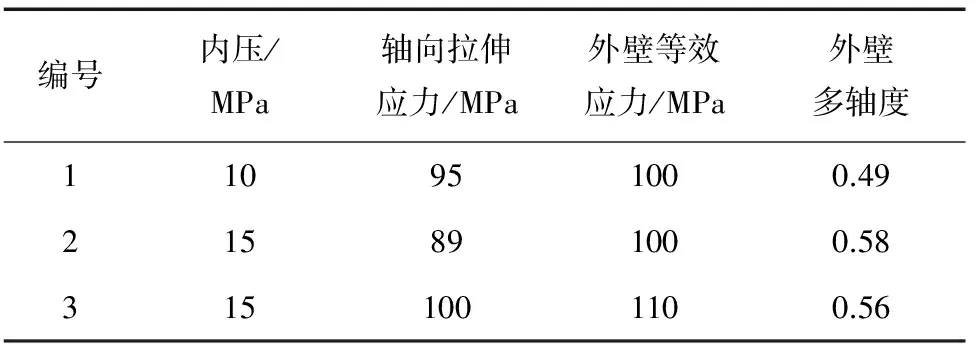
表2 蠕变试验载荷参数Tab.2 Load parameters for creep experiment

试验结束后测量试样断口的尺寸。在试样断口上取厚度约10 mm的圆环，切割成1/4圆环试样，对其轴向和环向截面进行粗磨、细磨、抛光,用体积分数4%的硝酸酒精溶液腐蚀后，利用JSM-6490LV型扫描电镜(SEM)观察其断口形貌和显微组织。

2 试验结果

多轴蠕变试验结束后，不同载荷组合下的试样均在标距间有效管段中间偏上或偏下位置断裂。由图3和表3可知，蠕变试验后试样断口处的外径减小，内径增大，管壁发生颈缩导致壁厚减薄，最终发生断裂。由表3还可以看出：在相同等效应力条件下，内压越大试样管壁的颈缩量越大，在相同内压条件下，等效应力越大管壁的颈缩量越大。

图3 断裂试样的宏观形貌Fig.3 Macroscopic morphology of fractured specimen

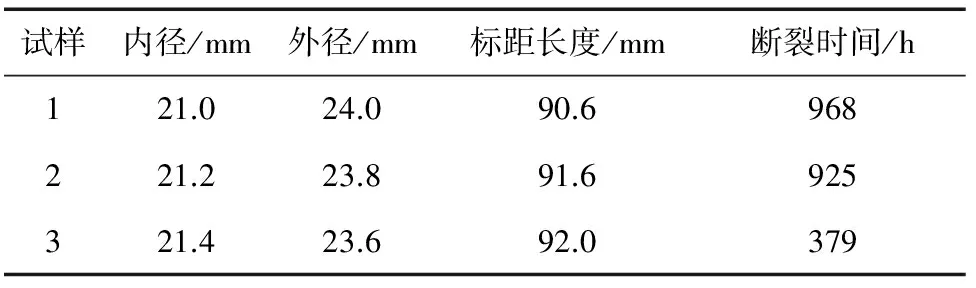
试样内径/mm外径/mm标距长度/mm断裂时间/h121．024．090．6968221．223．891．6925321．423．692．0379

由图4可知：试样3的外壁等效应力最大，最先发生断裂；试样1和试样2的外壁等效应力相同，试样2先于试样1断裂，这说明多轴度的增加会加速P92钢的断裂。

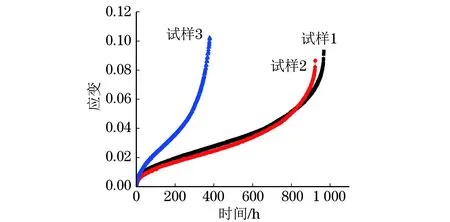
图4 不同试样的蠕变曲线Fig.4 Creep curves of different specimens

由图5可知：试样1断口中韧窝的尺寸最大、数量最少；试样3断口中韧窝的数量最多、尺寸最小；试样2断口中韧窝的数量和尺寸介于试样1和试样3之间。

图5 不同试样的断口形貌Fig.5 Fracture morphology of different specimens

由图6可以看出： 在试样1的轴向与环向截面中孔洞的数量和尺寸相当，孔洞基本分布于晶界和马氏体板条边界上；试样2轴向截面中孔洞的数量比环向截面中的多，孔洞尺寸也更大，这说明增加内压后，垂直于轴向的应力增大，导致孔洞沿环向方向长大，使具有较大多轴度的试样2比试样1更早发生断裂。综上可知，多轴度对蠕变孔洞的生长具有促进作用，从而影响P92钢的蠕变寿命。

图6 试样1和试样2环向与轴向截面的显微组织Fig.6 Microstructure of circumferential (a, c) and axial (b, d) sections for specimen 1 (a-b) and specimen 2 (c-d)

3 有限元分析及讨论

Kachanov-Robatnov(K-R)蠕变模型[12]常用于描述蠕变第二、第三阶段特性，但未考虑蠕变第一阶段特性和应力的多轴性。在K-R模型的基础上，加入描述蠕变第一阶段特性的方程，并考虑应力的多轴性及局部损伤效应[13]，改进后的K-R蠕变模型为

(1)

(2)

在650 ℃、内压和拉伸组合加载下P92钢的蠕变模型参数如表4所示。

考虑多轴蠕变试样的对称性，选取其1/4结构作为计算模型，采用SOLID186平面单元进行网格划分，有限元模型及加载方向如图7所示。

表4 P92钢的蠕变模型参数Tab.4 Parameters for creep model of P92 steel

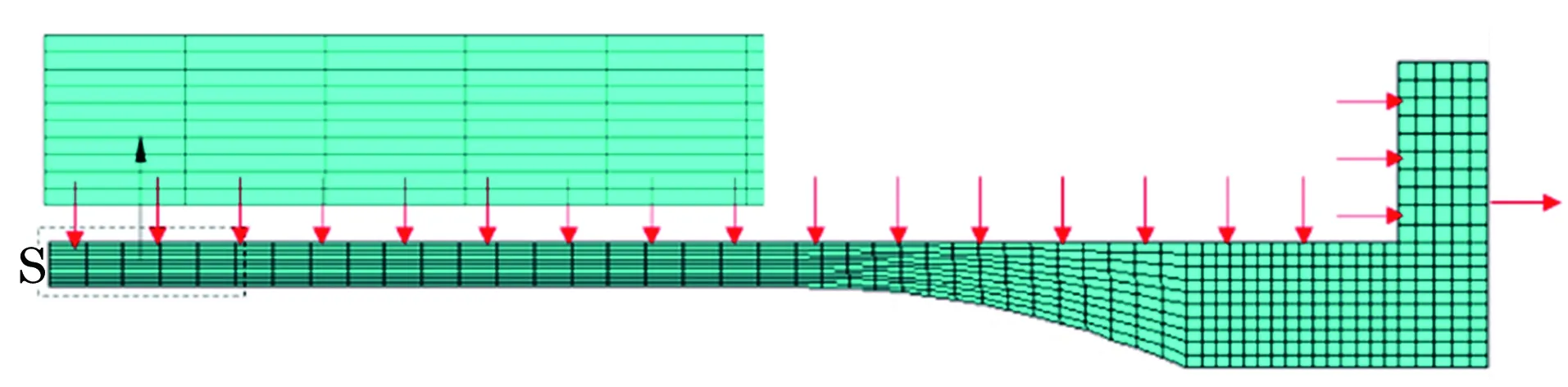
图7 多轴蠕变试样的有限元模型及加载方向Fig.7 Finite element model of multiaxial creep specimen and loading direction

将改进的K-R蠕变模型嵌入到有限元分析软件ANSYS中，根据表4中的模型参数计算在内压和拉伸组合加载下试样的蠕变曲线，并与试验结果进行对比。由图8可知，蠕变曲线的模拟结果与试验结果基本吻合。因此，该模型可用于模拟在内压和拉伸组合加载下P92钢的蠕变行为。

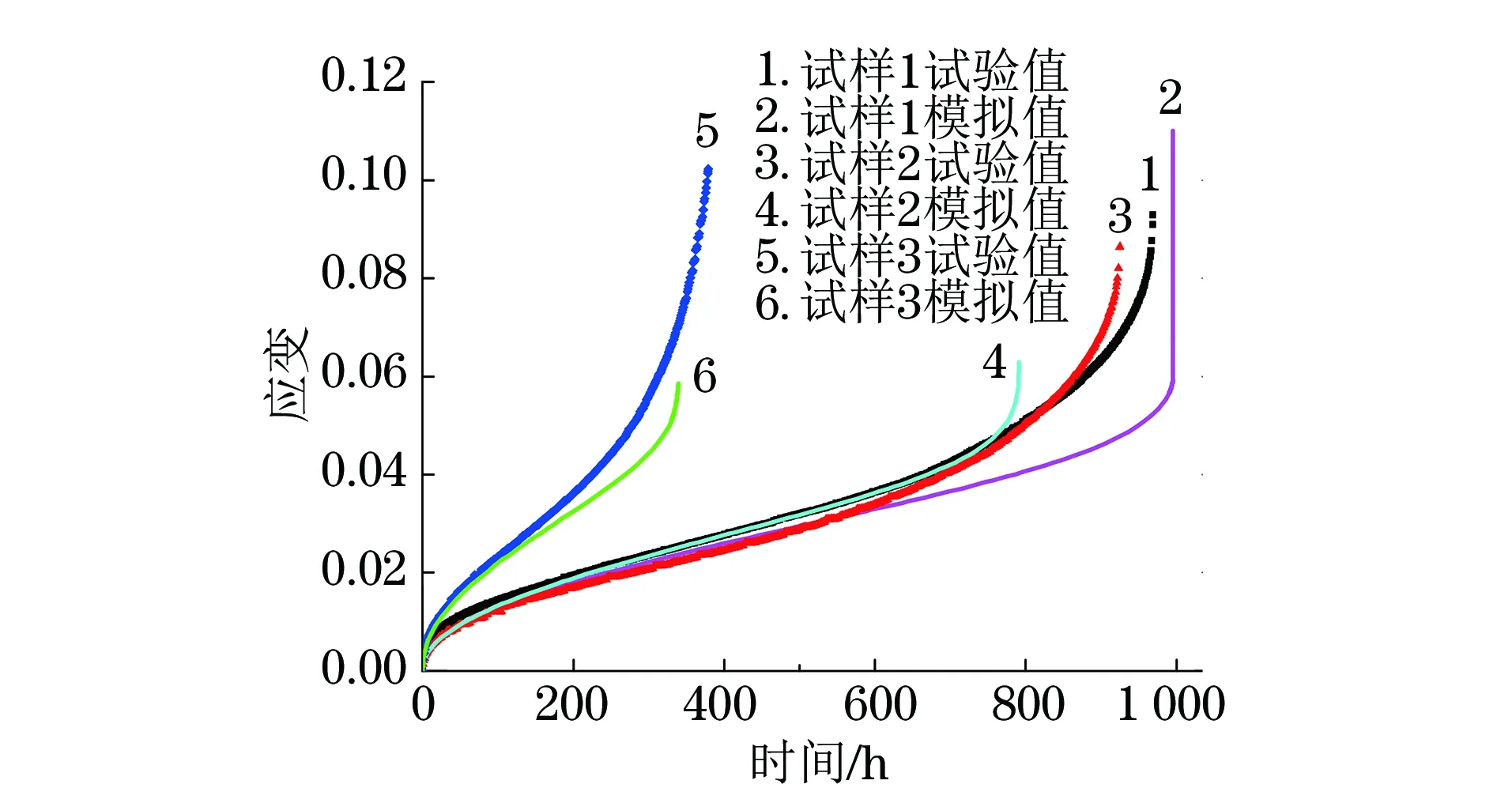
图8 不同试样蠕变曲线的模拟结果与试验结果的对比Fig.8 Comparison of simulation results with experiment results of creep curves of different specimens

从有限元模拟结果中提取试样外壁等效应力、第一主应力和多轴度随时间的变化曲线，并将时间做归一化处理，如图9所示，图中tr为断裂时间。

由图9可知：所有试样外壁等效应力和第一主应力均在加载初始时刻瞬间增加到一定值，之后随着时间的延长而逐渐减小；试样2的外壁多轴度始终大于试样1和试样3的，试样3的外壁多轴度介于试样1和试样2的之间。

在轴向拉伸应力100 MPa、内压15 MPa条件下，不同时刻的多轴度、等效应力、第一主应力和静水应力沿壁厚的变化曲线如图10所示，图中Ri为内径，Ro为外径，r为管壁不同厚度处的半径。

由图10可知：外壁多轴度大于内壁的，在蠕变第一阶段和第二阶段，多轴度基本不随试样壁厚的变化而变化，在蠕变第三阶段，损伤累积导致应力重新分布，多轴度也随之变化； 在蠕变初始阶段，等效应力、第一主应力和静水应力沿壁厚分布不均匀，外壁的第一主应力和静水压力均大于内壁的，外壁的等效应力小于内壁的；在蠕变过程中，内壁的这3种应力均先减小，之后维持在一个稳定范围，并且在蠕变断裂时刻突然增大；外壁的这3种应力均先增大，之后维持在一个稳定范围，并且在蠕变断裂时刻突然减小，这说明此时试样外壁已经变形失效。在蠕变过程中，试样在半径约为11.25 mm处的多轴度、等效应力、第一主应力和静水应力基本不随时间而变化，即为该试验条件下试样的骨点[14-15]。

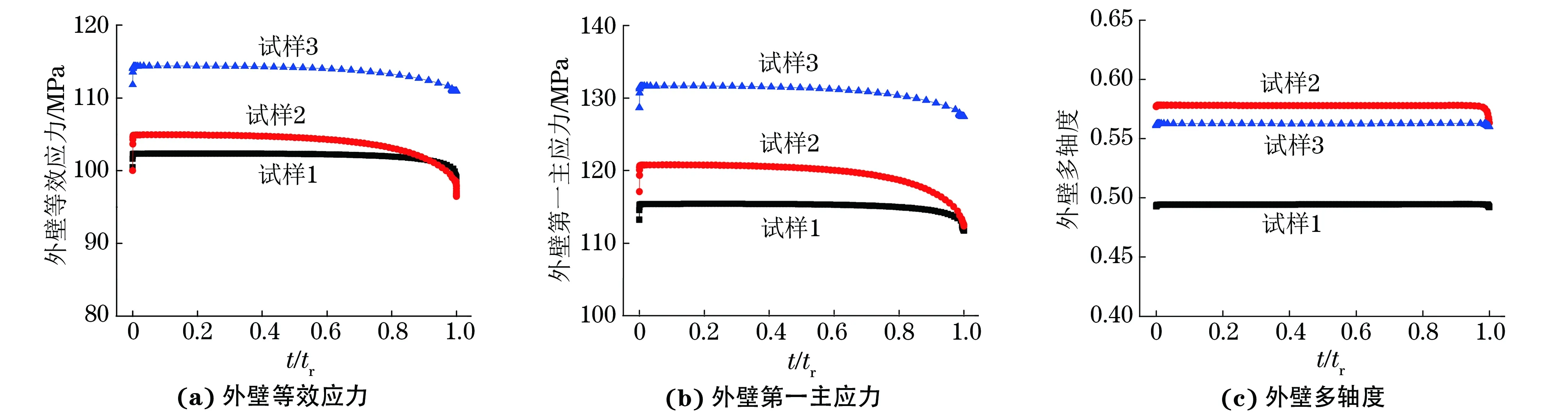
图9 不同试样外壁等效应力、第一主应力和多轴度随时间的变化曲线Fig.9 Curves of equivalent stress (a), the first principal stress (b) and multiaxiality (c) of outside wall vs time of different specimens

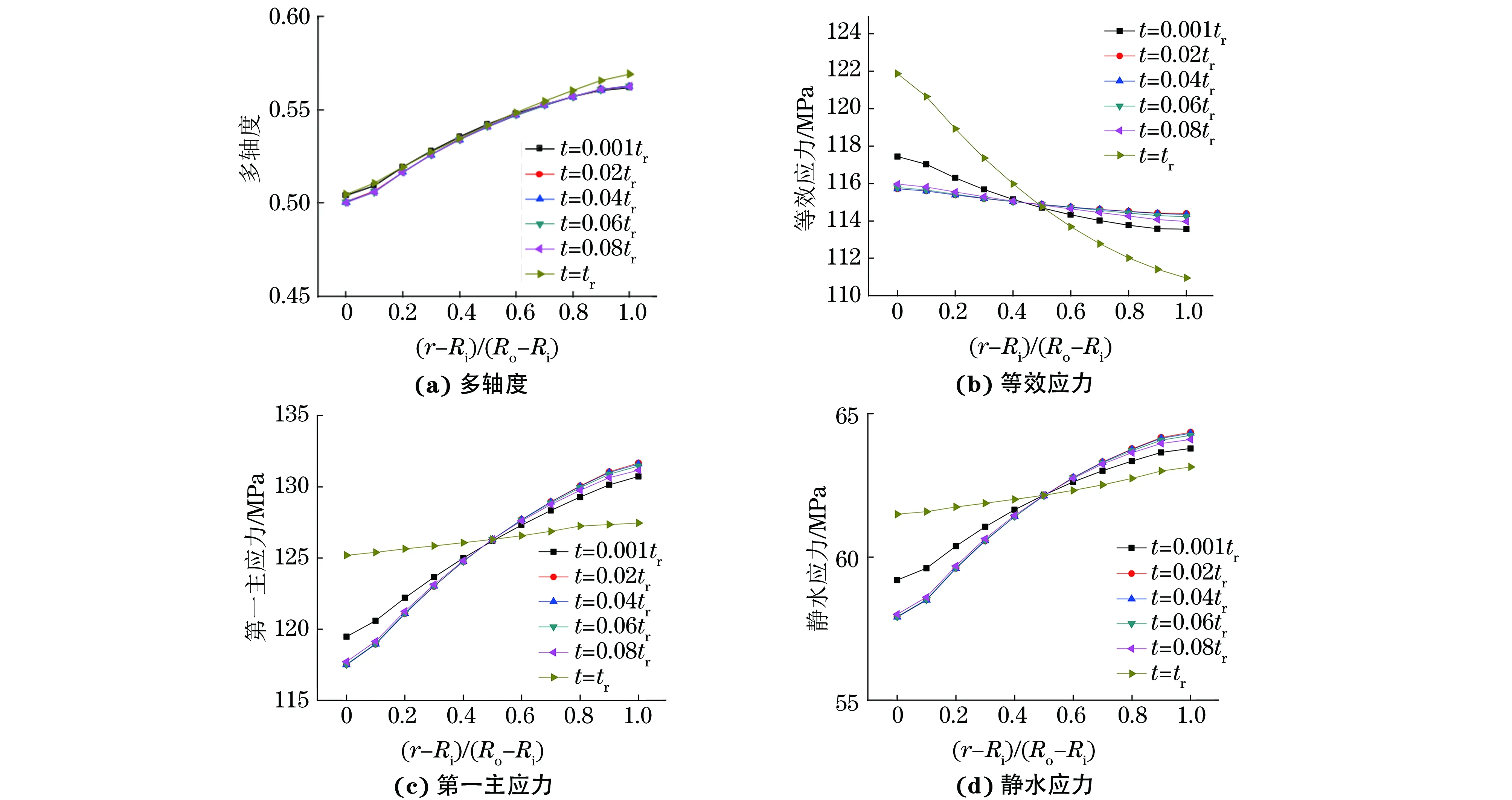
图10 在轴向拉伸应力100 MPa、内压15 MPa下蠕变过程中不同时刻的多轴度、等效应力、第一主应力和静水应力随试样壁厚的变化曲线Fig.10 Variation curves of multiaxiality, equivalent stress, the first principal stress and hydrostatic stress vs wall thickness during creep under 100 MPa axial tensile stress and 15 MPa inner pressure

图11为试样3有效管段损伤随时间的分布，其中左侧为试样内壁，右侧为外壁。由图11可知：试样有效管段的损伤沿壁厚分布不均匀，由于外壁的多轴度大于内壁的，使得外壁损伤的增长速率大于内壁处的。随着损伤的进行，外壁产生裂纹，试样的承载能力下降，应力重新分布，内壁的等效应力和第一应力增加，外壁的减小，最终导致试样断裂。综上所述，多轴度影响应力的分布，进而影响损伤的分布，多轴度大的位置其损伤程度也大，从而导致试样在该位置失效。

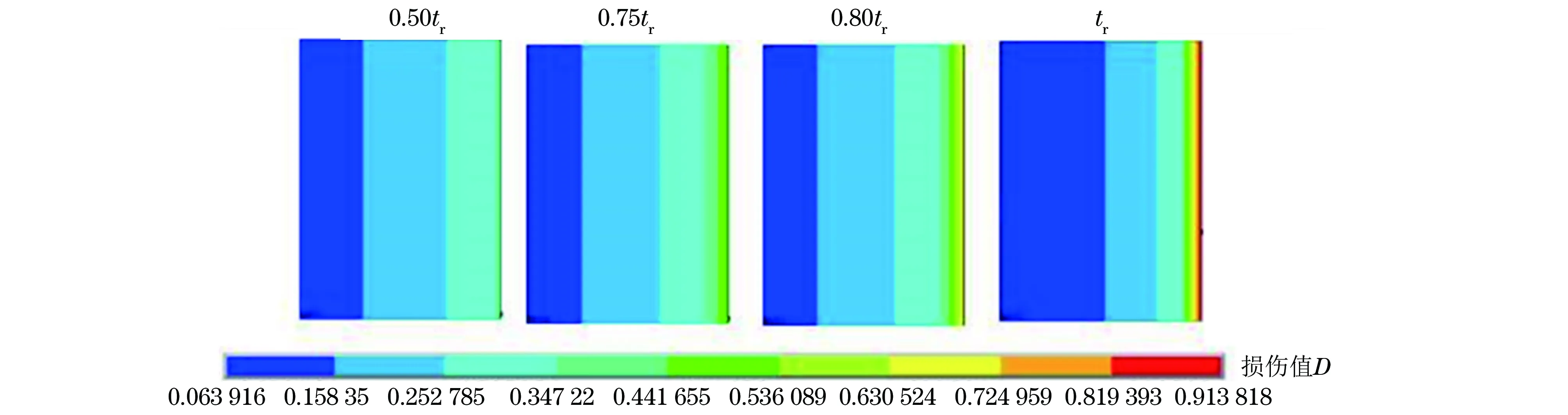
图11 试样有效管段损伤程度随时间的演变Fig.11 Evolution of damage degree vs time in effective pipe section of specimen

4 结 论

(1) 在内压和拉伸组合加载下，当外壁等效应力相同时，多轴度越大，P92钢的蠕变寿命越短；多轴度对P92钢蠕变孔洞的生长具有促进作用。

(2) 采用改进的K-R蠕变模型对650 ℃、内压和拉伸组合加载下P92钢的蠕变行为进行有限元模拟，模拟结果与试验结果基本吻合，该模型可以准确描述P92钢的蠕变行为。

(3) 在蠕变过程中，多轴度影响应力的分布，进而影响损伤的分布，多轴度大的位置其损伤程度也大。

[1] 耿鲁阳, 郭晓峰, 巩建鸣,等. 国产和进口P92耐热钢显微组织、拉伸和蠕变性能的对比[J]. 机械工程材料, 2014, 38(1):68-73.

[2] 姚华堂, 轩福贞, 沈树芳, 等. 高温材料的多轴蠕变试验方法[J]. 机械工程材料, 2008, 32(1): 5-9.

[3] JIANG Y P, GUO W L, YUE Z F. On the study of the creep damage development in circumferential notch specimens[J]. Computational Materials Science, 2007，38(4):653-659.

[4] NI Y Z, LAN X, XU H,etal. Finite element analysis and experimental research on notched strengthening effect of P92 steel[J]. Materials at High Temperatures, 2014, 31(2):185-190.

[5] GOYAL S, LAHA K. Creep life prediction of 9Cr-1Mo steel under multiaxial state of stress[J]. Materials Science & Engineering A, 2014, 615:348-360.

[6] 常愿,徐鸿,蓝翔. P92钢多轴蠕变本构模型的建立及验证[J]. 机械工程材料, 2017, 41(2): 112-118.

[7] WANG L Q, WANG J G, WANG H Y,etal. Interaction of fatigue and creep of GH33 under multi-axial stress at high temperature[J]. Journal of University of Science and Technology Beijing, 2003, 10(2):79-80.

[8] SELIGER P, GAMPE U. Life assessment of creep exposed components, new challenges for condition monitoring of 9Cr steels[J]. OMMI, 2002, 1(2): 2-14.

[9] YAO H T, XUAN F Z, WANG Z D,etal. A review of creep analysis and design under multi-axial stress states[J]. Nuclear Engineering and Design 2007, 237(18):1969-1986.

[10] HYDE T H, XIA L, BECKER A A. Prediction of creep failure in aeroengine materials under multi-axial stress states[J]. International Journal of Mechanical Sciences, 1996, 38(4):385-403.

[11] GOODALL I W, SKELTON R P. The importance of multiaxial stress in creep deformation and rupture[J]. Fatigue & Fracture of Engineering Materials & Structures, 2004, 27(4): 267-272.

[12] RABOTNOV Y N.Creep problems in structural members[M].Amsterdam：North-Holland Publishing Company，1969.

[13] 倪永中, 蓝翔. 一种用于P92钢寿命预测的蠕变模型研究[J]. 应用力学学报, 2014(6): 978-982.

[14] WEBSTER G A, NIKBIN K M, BIGLARI F. Finite element analysis of notched bar skeletal point stresses and dimension changes due to creep[J]. Fatigue & Fracture of Engineering Materials & Structures, 2004, 27(4):297-303.

[15] 刘学, 段向兵, 闫平, 等. P91钢高温蠕变的数值研究[J]. 电力建设, 2009, 30(5):52-55.