一种机载重轨干涉SAR相位偏移量估计算法
, ,
(1.中国科学院电子学研究所, 北京 100190;2.中国科学院大学, 北京 100049;3.空间信息处理与应用系统技术重点实验室, 北京 100190)
0 引言
机载重轨干涉SAR由于其飞行机动灵活、图像分辨率高、重访周期短等优点,能弥补星载SAR固有的缺点,特别适合对局部地区进行高精度地形测绘[1-2]、形变检测[3]和三维成像[4],具有较高的航空遥感运用价值。
在干涉SAR反演高程的过程中,绝对相位与解缠绕后的相位存在一个常数偏移量。目前方法利用在成像场景中人工部署并测量一定数量的定标点来计算常数偏移量。然而,实际工程中人为布设定标点浪费人力财力,尤其在一些危险区域部署和测量定标点是极其困难和难以实现的。为了解决这类问题,目前自动计算相位偏置的方法一般分为基于数据冗余的方法和基于外部DEM数据的方法。第一类方法中,文献[5]在双天线交轨干涉中对主、辅图像分别划分两个距离子带构成的差分干涉对来计算绝对相位。为了利用同一场景不同干涉数据之间的冗余性,文献[6]利用机载对飞模型的重叠区域建立的联合相位偏移函数来估计绝对相位;文献[7]通过联合多基线干涉来求解相位偏移量。第一类方法需要满足同一场景数据的冗余性,这限制了算法的普适性。第二类方法中,Perna针对机载双天线干涉SAR提出了利用外源DEM进行两步估计的方法[8],首先利用粗精度DEM中提取的控制点估计初步的相位偏移量,然后利用初估计出的相位偏移量反演得到精度较低的高程数据,再利用控制点处的高程差与相位满足的线性方程,采用最小二乘算法估计出第一步的估计误差,通过第二步的迭代估计从而提高估计精度。
然而,重轨干涉SAR由于两次飞行相互独立,因残余运动误差无法完全抵消而引入未知的时变基线误差。时变基线误差会改变算法[8]第二步中建立的模型与线性求解的匹配性能,从而消弱算法估计精度甚至导致算法的不适用。受限于目前惯性导航和差分GPS精度的限制,时变基线误差只能从数据中去估计。本文首先分析了时变基线误差对利用外源DEM估计相位偏移量的影响,然后提出嵌入了时变基线误差估计和补偿的干涉相位偏置估计算法,从而改善了算法在重轨干涉中的适用性,最后通过机载C波段重轨干涉DEM反演实验,验证了算法的有效性。
1 机载干涉SAR相位偏移量估计模型
令相位解缠后的相位为φuw, 与绝对相位φ之间存在相位偏置φoff:
φoff=φuw-φ
(1)
利用地面控制点(Ground Control Point, GCP)去求解时,需获得GCP较准确的地理信息,一般采用人为部署的角反射器。考虑从外源DEM提取的控制点作为定标点,外源DEM通过反向编码投影到机载斜地几何下,通过适当插值处理可以得到整个实验场景的高程信息,然后提取一定数量的控制点用于计算相位偏置量。设控制点数量为N(N>1),利用几何关系可以分别计算出控制点的绝对相位值φGCP,式(1)可以写成向量形式,即
φuw-1φoff=φGCP
(2)
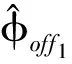

(3)
式中,N×N矩阵W=diag(m1,…,mk,…,mN),mk∈{0,1}表示掩膜标志。当控制点落入无效的掩膜区域时,其值mk=0,表明该点对估计没有贡献。相位偏置估计误差为
(4)


图1 利用外源DEM估计干涉相位偏置的流程图
由于重轨干涉SAR高程灵敏度方程中,Δh与β(x,r)具有如下线性关系:
Δh=β(x,r)·Δφ(x,r)
(5)
式中:
(6)
式(5)反映了地形高程变化所引起的相位变化存在一定的比例关系。λ为波长,r为斜距,B为基线,B⊥为垂直基线,θ为下视角。
基于式(5)和式(6),利用这个斜坡相位关系得到
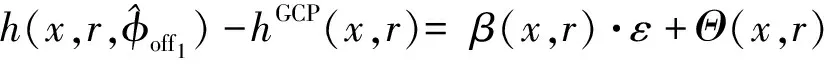
(7)

Θ(x,r)≈h(x,r,φoff)-hGCP(x,r)
(8)

将式(7)写成向量的形式,表示为
Δ=β·ε+Θ
(9)

由式(8)可知Θ是一个非零均值的矢量,此处将Θ写成均值项v和非零的矢量Θ0,即
Θ=1v+Θ0
(10)
式中,v表示利用InSAR重建的DEM与外源DEM的相对偏量。将式(10)代入式(9)可得
Δ=β·ε+1v+Θ0
(11)
所以,式(11)可以表达为一个线性模型:

(12)

(13)
其加权最小二乘解为
(14)
式中,N×N矩阵W=diag(m1,…,mk,…,mN),mk∈{0,1}表示掩膜标志。利用PBE和StopBE两步估计便可以估计出最终的相位偏置。
值得注意的是,式(12)能够采用最小二乘求解的前提是β-Δ具备线性性。实际上,β-Δ拟合的直线非常微弱地依赖于外源DEM的随机波动误差[8]。导致外源DEM波动误差与β是相互独立的,特别是当利用机载InSAR产生的DEM与外源DEM彼此独立的情况。这并不意味着向量β的方差越小, StopBE估计就越准确。从式(13)可以看出,估计误差是将式(12)中的噪声Θ0投影到由系统矩阵H的列向量所展开的子空间,这个投影与HTH的行列式呈反比例关系:
(15)
式(15)表明估计误差与β的方差呈比例关系,其比例常数为N2。更重要的是,式(15)中β的方差越大,式(13)引入的估计误差就越小。因此, StopBE特别适合于机载干涉,因为机载干涉SAR具有较宽的下视角θ,β方差就特别大。
2考虑时变基线误差补偿的相位偏置量估计模型
2.1 时变基线误差对相位偏置量估计算法的影响
时变基线是完全随机的,本小节进行数值仿真实验。雷达参数和基线信息如表1所示,仿真场景区的高程如图2(a)所示,依据雷达参数和场景高程得到的绝对干涉相位如图2(b)所示。仿真试验时在图2(b)中人为加入相位偏置量。由于外源DEM存在误差,从DEM提取出的控制点的高程误差可视为随机噪声,假设其满足均值为μ、方差为σ2的高斯随机分布G(μ,σ2),并按照均匀分布原则选取不同位置的控制点。通过控制μ和σ2,从而模拟不同精度的DEM误差。
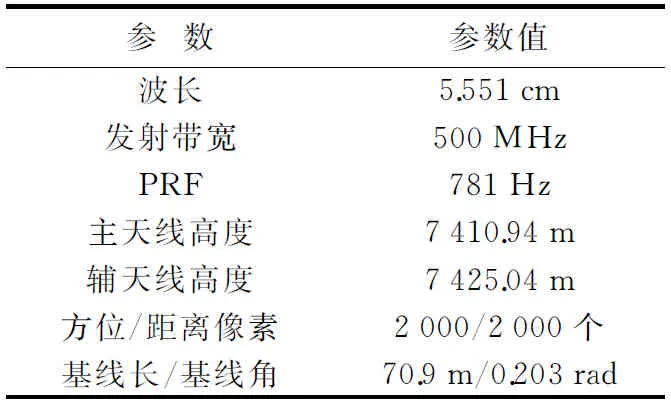
表1 仿真时雷达参数和基线信息
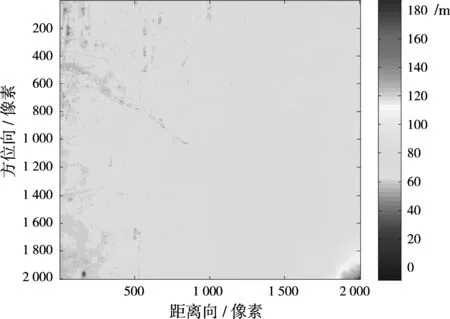
(a)场景高程

(b)根据雷达参数和地形仿真的绝对相位图2仿真场景的高程图及干涉绝对相位
为了说明时变基线的影响,实验中增加了时变基线误差。所加入的时变基线误差的水平分量dx和竖直分量dz如图3(a)所示。时变基线误差引起的每个像素的相位误差如图3(b)所示,可以看到时变基线误差表现为相位波动。
为了定量分析时变基线对PBE和StopBE估计的影响,分别仿真了不同精度的DEM下的情况,设置了μ=10 m, σ=0, 0.5,…,5 m的情况和σ=2 m, μ=-10,-9,…,10 m的情况,从DEM中提取了1 000个地面控制点用于估计相位偏置,并给出了利用PBE和StopBE估计相位偏置反演出的高程误差随σ和μ的变化关系。图4为μ=10 m,σ=0, 0.5,…,5 m的实验结果,其中图4(a)为没有添加时变基线误差的结果,图4(b)为添加了时变基线误差的结果。图5为σ=2 m,μ=-10,-9,…,10 m的实验结果,图5(a)和图5(b)分别对应没有添加时变基线误差和添加了时变基线误差下的估计结果。从实验结果可以看出,尽管DEM噪声对PBE估计影响很大,但在不存在时变基线误差的情况下,选择一定数量的GCP点,通过PBE+StopBE的迭代估计的结果总能达到一个比较小的误差;然而,在存在时变基线误差的情况下,PBE+StopBE算法无法获得一个较好的结果。因此,相位偏置估计算法在重轨干涉中运用时必须考虑时变基线误差的补偿。

(a)添加的时变基线误差
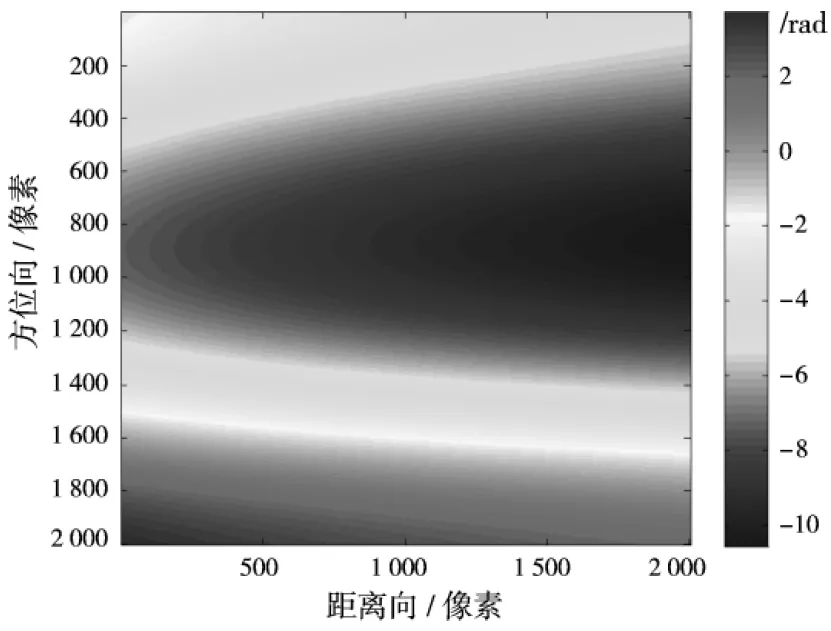
(b)时变基线误差导致的相位误差图3 仿真添加的时变基线误差分量及其导致的相位误差
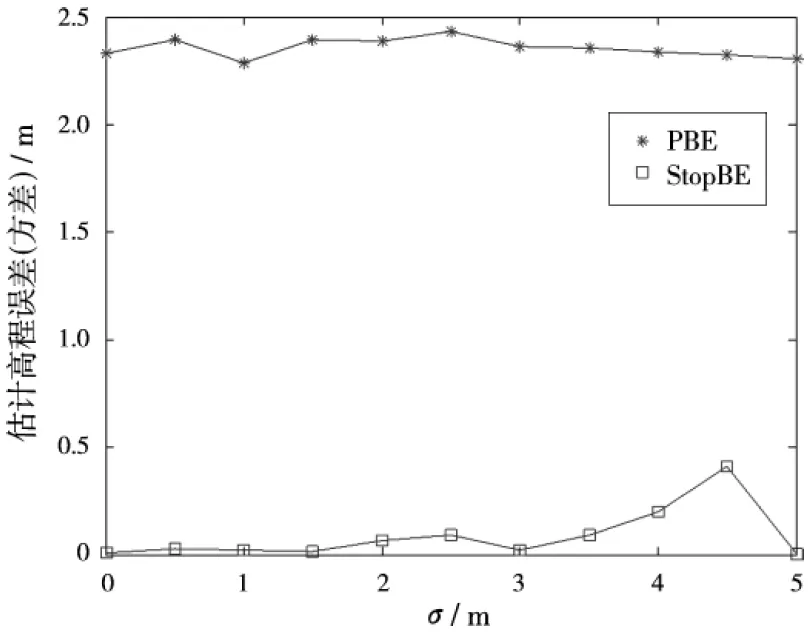
(a)不存在时变基线误差的情况

(b)存在时变基线误差的情况图4μ=10 m, σ=0, 0.5,…,5 m时PBE和StopBE估计相位偏置反演出的高程误差随σ的变化关系
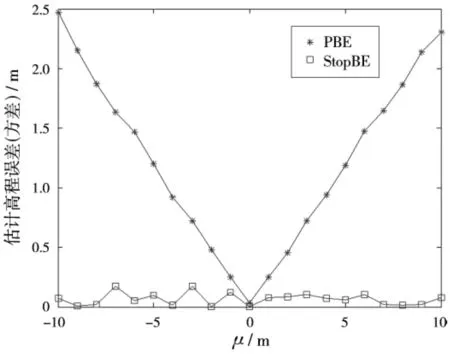
(a)不存在时变基线误差的情况

(b)存在时变基线误差的情况图5μ=-10,-9,…,10 m, σ=2 m时PBE和StopBE估计相位偏置反演出的高程误差随μ的变化关系
本文第1节分析过,StopBE采用最小二乘估计的前提是β-Δ的线性性能够得到保持。图6是不存在时变基线误差(图6(a))和存在时变基线误差(图6(b))时的β-Δ的关系及其拟合的直线。可以看出,不存在时变基线误差的情况下,β-Δ的线性性能够得到很好的保持。当时变基线误差存在时β-Δ的线性性变差,从而影响了StopBE估计结果。由于时变基线是完全随机和未知的,此处无法写出其具体的解析表达式。然而,可以通过从数据域中估计并补偿时变基线误差,减小其对β-Δ的影响,以确保相位偏置量估计算法能够使用。
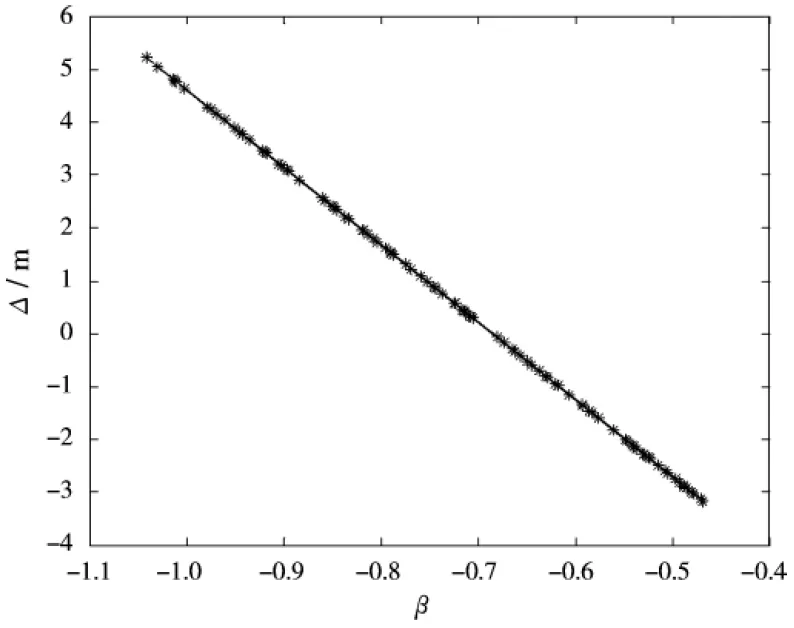
(a)不存在时变基线误差的情况

(b)存在时变基线误差的情况
图6不存在和存在时变基线误差时的β-Δ的关系
2.2 时变基线误差估计与补偿算法
多斜视(Multisquint)方法[9]估计时变基线误差时利用了方位配准误差与不同子视图像差分相位的关系。为了绕开低相干区目标对时变基线误差估计的影响,改进的多斜视(Refined Multisquint)方法[10]被提出并成功用于估计时变基线误差。对经过配准后的主S1、辅S2图像分别划分K个子孔径图像,通过计算相邻子孔径的干涉相位差,可以得到K-1个差分干涉相位。第k个差分干涉相位表达为
(16)
对差分干涉相位进行加权平均就得到时变基线的一阶导数[10]:



(18)

Abxz=blos
(19)
式中:
(20)
(21)
(22)
其加权最小二乘解为
bxz=(ATWA)-1ATWblos
(23)
式中,加权矩阵W为
(24)


图7 时变基线的距离空变几何模型
通过对计算出的时变基线导数进行积分可以求解出时变基线误差,未知的时变基线常数项可以利用外部DEM来消除,然后把计算出的时变基线误差补偿到最终的干涉相位上。
2.3 嵌入时变基线误差补偿的相位偏置量估计算法
重轨干涉SAR系统双通道重复飞行的运动误差相互独立,无法完全相互抵消,因而引入了未知的时变基线误差,所以必须采用残余运动误差补偿算法,减小时变基线误差φΔ对相位偏置估计算法的影响。图8是嵌入了时变基线误差估计的相位偏置估计算法。首先通过多斜视算法估计时变基线误差,并对相位进行修正,然后用修正之后的相位结果进行相位偏置估计。该算法也可以迭代进行,以提高估计精度。
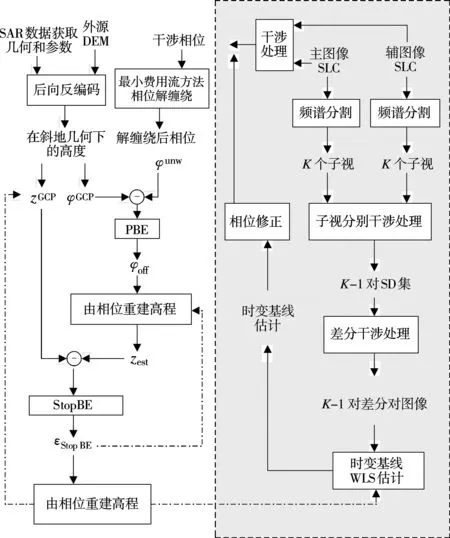
图8 考虑时变基线误差估计的相位偏置估计算法流程(虚线框为时变基线估计算法)

时变基线导数对频谱间隔Δfsub的敏感度因子为
(25)
时变基线误差的导数估计的标准差为
(26)
由此可知: 1) 划分子视图像数量K越多,越有利于提高时变基线导数估计的精度,然而划分数量过多,会导致图像信噪比变低,相干系数变低,从而使得差分干涉相位噪声标准差增大,故实际处理时要综合考虑; 2) 频谱间隔越大,越有利于提高时变基线导数的估计精度,但频谱间隔过大,会导致划分的子孔径带宽偏小,会使干涉相位图中的噪声标准差变大,需要权衡考虑。
3 实测数据处理
为了验证本文算法的有效性,对中国科学院电子学研究所的C波段机载重轨干涉SAR系统获取的重轨干涉SAR数据进行处理。重轨干涉SAR参数如表2所示,成像算法采用了Ewk+DMA[11]+PTA[12]算法以减小运动补偿带来的误差量,得到了聚焦良好的SAR图像。

表2 重轨干涉SAR参数
处理场景中包括了3个定标点(A,B和C),场景幅度图和定标点位置如图9所示。实验中使用的DEM数据为垂直精度20 m、水平精度30 m的Aster DEM数据。Aster DEM转化为对应场景高程数据,如图10所示。图像的多普勒有效带宽为270 Hz,为了兼顾图像信噪比和时变基线导数估计的精度,对配准之后的主、辅图像分别划分7个方位向子孔径,每个子孔径为38.57 Hz。采用本文方法估计和补偿时变基线误差,估计出来的时变基线的水平和竖直分量如图11所示,估计出的残余运动基本上在mm量级。
时变基线误差补偿之后,干涉处理时对方位进行了四视处理,去除平地并相位滤波之后的干涉结果如图12所示。为了比较方法的有效性,此处对比了3种算法的结果:第一,先利用3个角反射器A,B,C计算出了相位偏置,然后反演高程,结果如图13所示;第二,利用Aster DEM提取均匀分布的2 000个GCP点,并利用PBE+StopBE算法,迭代3次计算出相位偏置;第三,利用考虑了时变基线误差估计的相位偏置估计方法,迭代3次计算出相位偏置,最后反演出的高程如图14所示。3种情况估计出的相位偏置及在A,B,C定标点处反演的高程结果如表3所示。
通过比较实验结果可以发现:直接利用定标点估计相位偏置,反演出的高程精度在2 m左右;直接利用Aster DEM提取控制点,采用PBE+StopBE迭代估计相位偏置,反演出的高程精度在6 m以内;利用本文改进的方法,即考虑了时变基线误差估计和补偿的相位偏置估计方法,最终反演出的高程误差在4 m以内。改进后的方法减小了时变基线误差对无人工控制点相位偏移量估计算法的影响,提高了DEM重建精度,适用于场景中无定标点的机载InSAR的DEM反演。

图9 实验场景幅度图(A,B,C分别表示3个角反射器定标点)

图10 从Aster DEM 转化过来的对应成像场景的高程图

图11 估计到的时变基线水平和竖直分量

图12 去平地后的干涉相位

图13 利用角反射器估计相位偏置最后反演出来的高程图

图14 利用Aster-DEM数据按照本文方法计算相位偏置并反演的高程图

表3 实验结果比较
4 结束语
本文详细分析了时变基线误差对机载重轨干涉SAR相位偏置量估计算法的影响,指出了时变基线误差会降低估计模型与线性求解的匹配性能,从而消弱算法估计精度的问题。针对这个问题,本文提出了嵌入时变基线误差估计和补偿的相位偏置量估计算法。最后利用机载C波段0.5 m高分辨率重轨干涉SAR实测数据验证了该算法的有效性,并结合地面定标点验证了该算法的高程重建精度在4 m以内。该方法简单快速,消除了机载重轨干涉SAR获取DEM时对人工定标点的依赖性,适用于无定标点情况下机载InSAR的DEM反演。
[1] 徐华平,陈杰,周荫清,等. 干涉SAR三维地形成像数据处理技术综述[J]. 雷达科学与技术, 2006, 4(1):15-21.
XU Huaping, CHEN Jie, ZHOU Yinqing, et al. A Survey of Interferometric SAR Topography Mapping Data Processing Technique[J]. Radar Science and Technology, 2006, 4(1):15-21.(in Chinese)
[2] 方东生,吕孝雷,李缘廷,等. 运动补偿对机载SAR重轨干涉成像的影响分析[J]. 雷达科学与技术, 2016, 14(4):355-363.
FANG Dongsheng, LYU Xiaolei, LI Yuanting, et al. Effect of Motion Compensation on Airborne Repeat Pass InSAR Imaging[J]. Radar Science and Technology, 2016, 14(4):355-363.(in Chinese)
[3] NEUMANN M, HENSLEY S, AHMED R, et al. UAVSAR PolInSAR and Tomographic Products for Natural Media Characterization[C]∥10th European Conference on Synthetic Aperture Radar, Berlin, Germany:VDE, 2014:225-228.
[4] TEBALDINI S, NAGLER T, ROTT H, et al. Imaging the Internal Structure of an Alpine Glacier via L-Band Airborne SAR Tomography [J]. IEEE Trans on Geoscience and Remote Sensing, 2016, 54(12):7197-7209.
[5] MADSEN S N, ZEBKER H A. Automated Absolute Phase Retrieval in Across-Track Interferometry[J]. International Geoscience and Remote Sensing Sympo-sium, Houston, TX:IEEE, 1992:1582-1584.
[6] MURA J C, PINHEIRO M, ROSA R, et al. A Phase-Offset Estimation Method for InSAR DEM Generation Based on Phase-Offset Functions[J]. Remote Sensing, 2012, 4(3):745-761.
[7] GATTI G, TEBALDINI S, D’ALESSANDRO M M, et al. ALGAE:A Fast Algebraic Estimation of Interferogram Phase Offsets in Space-Varying Geometries [J]. IEEE Trans on Geoscience and Remote Sensing, 2011, 49(6):2343-2353.
[8] PERNA S, ESPOSITO C, BERARDINO P, et.al. Phase Offset Calculation for Airborne InSAR DEM Generation Without Corner Reflectors[J]. IEEE Trans on Geoscience and Remote Sensing, 2015, 53(5):2713-2726.
[9] SCHEIBER R, MOREIRA A. Coregistration of Interferometric SAR Images Using Spectral Diversity[J]. IEEE Trans on Geoscience and Remote Sensing, 2000, 38(5):2179-2191.
[10] REIGHER A, PRATS P, MALLORQUI J J. Refined Estimation of Time-Varying Baseline Errors in Airborne SAR Interferometry [J]. IEEE Geoscience and Remote Sensing Letters, 2006,3(1):145-149.
[11] MENG D, HU D, DING C. A New Approach to Airborne High Resolution SAR Motion Compensation for Large Trajectory Deviations [J]. Chinese Journal of Electronics, 2012, 21(4):764-769.
[12] DE MACEDO K A C, SCHEIBER R. Precise Topography and Aperture Dependent Motion Compensation for Airborne SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(2):172-176.

