天地波高频超视距雷达阵列校准方法

， ，

(武汉大学电子信息学院， 湖北武汉 430072)

0 引言

随着天波、地波雷达技术发展日益成熟，基于天波反射/地波绕射传播模式的天地波高频雷达系统以其独特的优点受到人们的重视。在天波反射/地波绕射的模式中，通过天波发射模式将高频电磁波斜入射到电离层，经电离层反射到达海面，再经海面以表面波的形式绕射传播到接收点[1]。这种新的传播模式充分利用了天波雷达探测距离远以及地波雷达不受电离层影响的特点[2]，实现了两者优势互补。

武汉大学研制的天地波高频超视距雷达采用MUSIC超分辨算法进行海流DOA估计，其基本原理是根据Barrick提出的一阶海洋回波理论，对接收到的后向和非后向散射回波进行MUSIC超分辨空间谱估计，提取海流DOA信息[3-4]。以MUSIC为代表的超分辨算法在接收阵列的阵列流型精确已知的情况下，能够准确地估计信号的来波方向，同时计算多个DOA。而实际情况下，因为各种模型误差的存在，使得这类算法的性能大大降低甚至失效[5-6]，因此必须对阵列进行幅相误差校准。

阵列误差校正方法可以分为两大类：有源校正法和自校正法。其中有源校正法是通过在空间设置方位精确已知的辅助信源，来对阵列扰动参数进行离线估计[7-8]；自校正法不需要有源校正中所依赖的辅助信源，可以在线完成实际方位估计，校正精度比较高，但是目前大部分自校正算法往往需要增加扰动参数的假设，设计高维、多模非线性优化，计算量非常大，且参数估计的全局收敛性往往无法保证[9]。

2016年初，武汉大学海态实验室在福建沿海进行了天地波组网试验，站点包括赤湖、东山和龙海三个地波雷达站以及位于武汉大学的天波雷达站。本次试验成功实现了天发地收、地发地收的分布式同步组网海洋探测，对于每个地波雷达站除了接收本站发射信号与海面相互作用的后向散射回波外，还能同步接收来自其他各站发射信号与海面相互作用的非后向散射回波和直达波信号。对于分布式高频超视距雷达系统，各站点方位精确已知，使得利用信噪比高的直达波信号对接收阵列进行校正成为可能。文献[10]提出了利用直达波信号，基于协方差矩阵的特征结构来估计双基地高频地波雷达发射通道的幅相误差参数，由于接收平台处于运动状态，且直达波的距离只能通过估计得到，使得幅相误差估计的精度降低。另外，该文中只进行了计算机仿真，没有用实测数据进行验证。文献[11]提出使用方位已知的直达波信号的多普勒谱来估计通道幅相误差，避免了传统自校准方法的迭代过程，但只是针对地波雷达系统的阵列幅相误差的校准。

本文针对天地波高频超视距雷达系统自身的特点，通过回波的偏置信息[12]提取组网系统中其他站的直达波信号，计算得到幅相误差值，并在对天、地波回波进行校准前采用高斯函数累加模型对幅相误差值进行优化。通过对比优化前后反演得到的海流结果，证明了该方法的有效性。

1 阵列信号模型

考虑一个M阵元的天线阵列，有D个平面波入射到该天线阵，假设阵元数等于通道数。入射波是窄带信号，中心角频率为ω0，不考虑阵列误差，则接收阵列信号为

m=1,2,…,M

(1)

式中，si(t)表示第i个入射信号，nm(t)表示第m个阵元的加性噪声。将上式用矩阵形式表示：

(2)

其矢量形式为

X(t)=AS(t)+N(t)

(3)

式中，X(t)为阵列的M×1维快拍数据矢量，N(t) 为阵列的M×1维噪声数据矢量，S(t)为空间信号的D×1维矢量，A为空间阵列的M×N维流型矩阵(导向矢量)，且

A=[a1(ω0)a2(ω0) …aD(ω0)]

(4)

其中，导向矢量

(5)

考虑接收阵列为均匀的直线阵，相邻阵元的间距为d，信号入射方向与阵列法向的夹角为θ，天线的阵列模型如图1所示。

图1 均匀直线阵结构示意图

以阵列的第一个阵元作为参考阵元，则

(6)

均匀直线阵的导向矢量为

(7)

当考虑阵列幅度和相位误差时，阵元接收信号可以表示为

X(t)=ΓA(θ)S(t)+N(t)

(8)

式中，Γ=diag{Γ1,Γ2,…,ΓM}为幅相误差矩阵。

2 阵列幅相误差有源校正

利用辅助源校正的基本思路为：通过在远场放置一个距离和方位已知的辅助信号源，实现对接收阵列的校准。

2.1 有源校正原理

假设在阵列远场存在一个方位为θ的信号源。阵列快拍数据的协方差矩阵为

Rxx=E[X(t)XH(t)]=

ΓARssAHΓH+σ2I

(9)

式中，Rss=E[S(t)SH(t)]为信号协方差矩阵，Γ为幅相误差矩阵，I为单位矩阵。

对协方差矩阵进行特征值分解，由于信号子空间与阵列流型空间为同一个空间。当为单个信源时，最大特征值对应的特征向量e1与信号导向矢量a(θ)满足：

Γa(θ)=ke1

(10)

式中，k为未知复常数。如果以阵列中的1号阵元为参考阵元，即幅度误差系数为1，相位误差系数为0，这样能够确定常数k。从而得到幅相误差矩阵其他误差系数：

(11)

2.2 直达波校正

在分布式高频超视距雷达系统中多个雷达是同步工作的，每个雷达站除了接收通过海面散射后的回波外，还能接收其他站的高信噪比直达波。由于这些直达波信号的方位能够通过雷达站GPS定位准确地获取，因此为接收阵列的校准提供了一个高精度的辅助源。

3 阵列幅相误差系数优化

在实际雷达工作中，由于信号会受到杂波和环境影响，导致某一时刻或某一时间段的直达波信号不稳定，从而使得幅相校准值的稳定性变差。采用这些非稳定校准值进行补偿会使得MUSIC算法进行海流DOA估计的准确性大大降低。因此，校准值优化对后续海流反演具有重要的意义。

3.1 高斯函数累加模型

若P={p1,p2,…,pn}为一段有限时间内的校准值序列，pi对应第i个均匀时间间隔的校准值。待优化校准值pi前后两个子序列长度分别为n1，n2，生成新校准值序列：

W(n1,n2,i)={pi-n1,pi-n1+1,…,pi,…,pi+n2}

(12)

式中，n1+1≤i≤n-n2。假设对于每一个校准值都对应一个高斯函数：

(13)

将序列W中所有校准值对应的高斯函数累加：

(14)

若øi(y0)为函数øi(x)的最大值，则优化后的校准值大小为y0，即pi=y0。

对上式分析可知，函数最高峰对应的校准值代表该段时间内的稳定值。由于不稳定点处的累加值较小，因此能够被有效地剔除，然后利用稳定值进行修正，从而达到优化的目的。图2为n1=6，n2=12时校准值优化示意图。

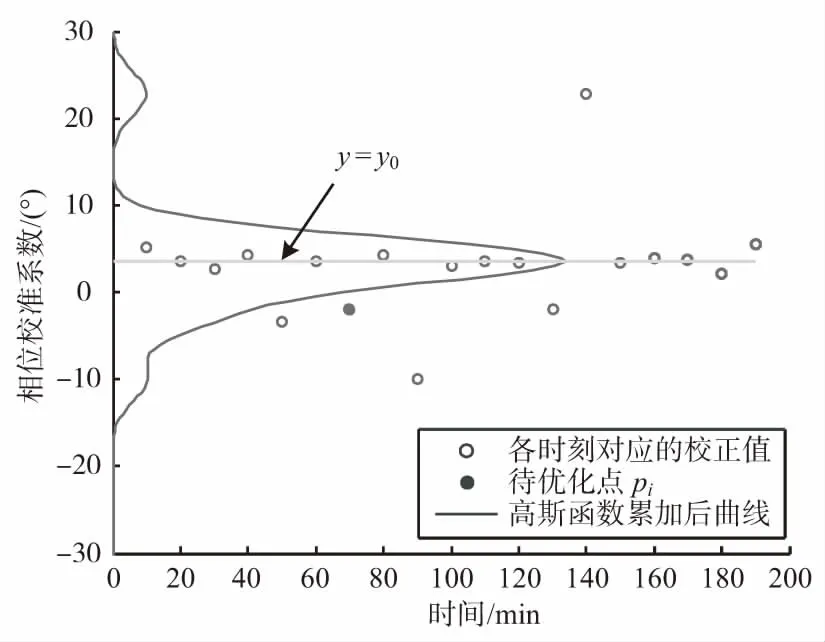
图2 校准值优化示意图

3.2 校准值优化

对一段时间内的校准值序列采取滑动的办法连续设置待优化点，最终得到优化后的校准值序列：

(15)

图3为一段时间内相位校准值的变化情况，可以看到在某些时刻校准值存在明显跳变。采用3.1节的模型对校准值序列进行优化。根据大量实测数据校准值的稳定程度，可设置高斯函数参数A=1，σ=2.5。

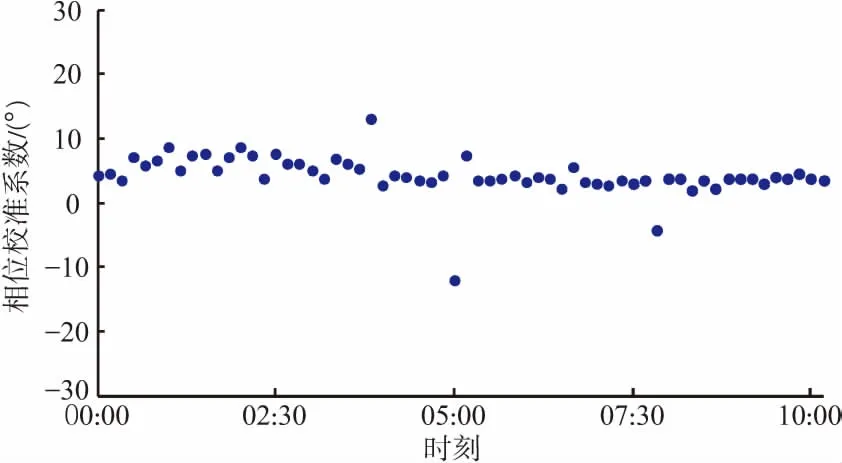
图3 优化前校准值

图4为图3对应的相位校准系数优化前后的对比结果。可以看出，经优化后校准值稳定性有了明显提高。

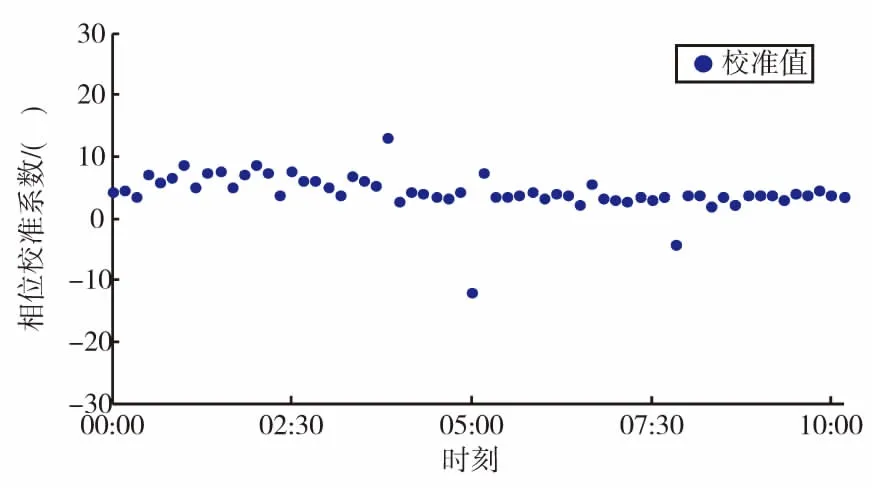
图4 优化前后校准值对比

4 实测数据分析

2016年上半年，武汉大学在福建沿海进行了天地波混合组网海洋探测试验。该组网系统由龙海、赤湖和东山三个地波雷达站以及武汉大学天波雷达站组成，因此存在天波发射/地波接收和地波发射/地波接收两种工作模式。另外，每个地波雷达站处于双频工作状态，分别为7.77 MHz和12.47 MHz，发射天波频率为7.77 MHz。图5为东山站接收信号的距离多普勒谱，谱图中包含了各站高低频信号，根据各站预先设置的偏置信息和雷达站的地理位置可以将它们分离开，通过提取某一个站的直达波信号对阵列幅相误差进行校正，对校准后的数据利用MUSIC算法进行到达角估计，最终得到海洋状态信息。

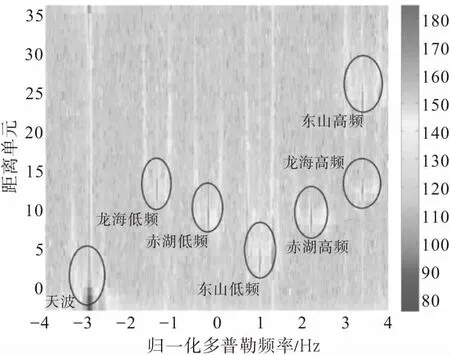
图5 东山距离多普勒谱

选取2016年2月12日00:00 — 20:00东山站探测数据进行分析，采用龙海直达波信号对采集到的频率为7.77 MHz的天、地波数据进行幅相误差校准。首先提取龙海站频率为7.77 MHz对应的直达波,计算得到阵列各通道幅相误差值，然后采用高斯函数累加模型对误差值进行优化。表1为优化前后直达波校准统计结果，可以看到优化后的幅相校准值的稳定性更高。

表1 优化前后直达波校准统计结果

为了验证该优化方法的有效性，将优化前后的校准结果应用到高频超视距雷达后续数据处理中，进行海洋表面流信息的提取。试验期间，在距离东山站72 km处放置了测流定点浮标。将优化前后反演得到的海流结果与浮标测量的流速进行比较，结果如图6所示，可以观察到优化后的探测结果更接近浮标测量结果。

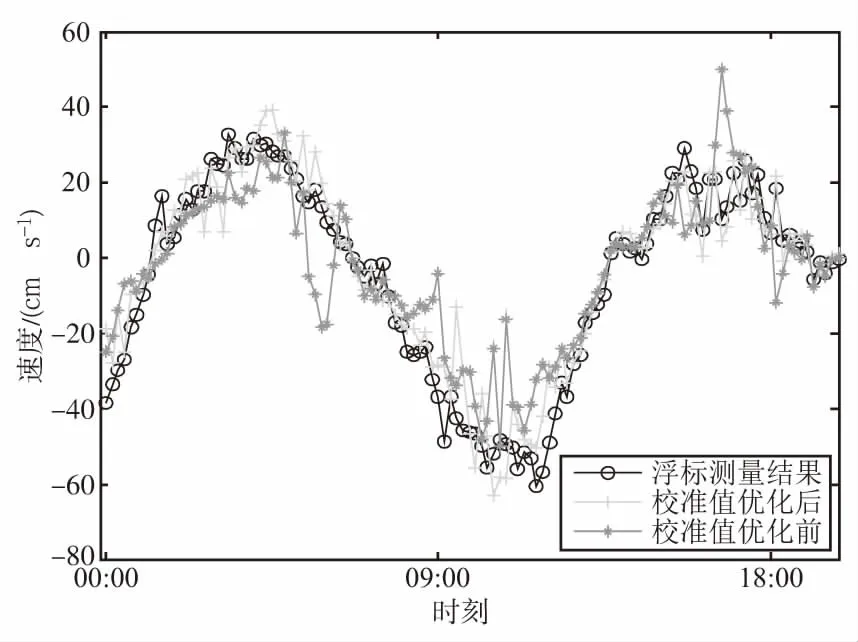
图6 校准值优化前后雷达探测结果与浮标测量流速

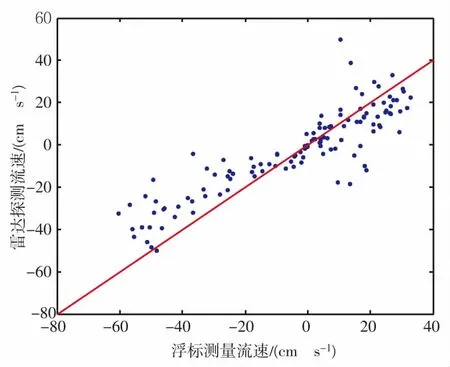
(a)优化前

(b)优化后图7 校准值优化前后海流结果散点图

图7给出了校准值优化前后对应海流结果散点图，可以看到对幅相校准值先进行优化后补偿得到的雷达探测结果明显优于直接补偿的结果，从而表明了该优化方法的有效性。表2给出了相应的统计参量。

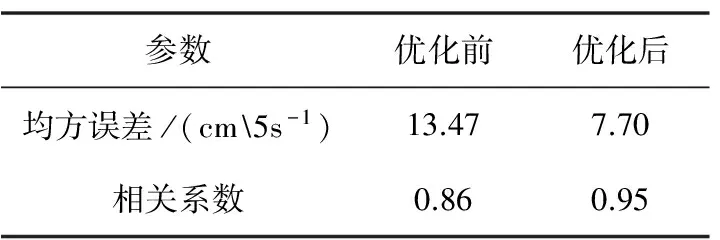
表2 校准值优化前后海流结果对比统计

5 结束语

通道幅相误差的不一致性会导致MUSIC超分辨算法性能下降甚至失效，因此必须对阵列各通道进行校准。针对天地波高频超视距雷达，本文研究了一种阵列幅相误差校准方法。该方法首先根据回波的偏置信息以及各站的地理位置提取方位已知的直达波信号，计算得到幅相误差值，然后针对信号会受到杂波和环境影响导致校准值稳定性变差这一现象，提出了一种基于高斯函数累加模型的校准值优化方案。分别采用优化前后的校准值进行补偿，并提取海洋表面流结果与浮标数据对比，验证了该方法的可靠性。

[1] 朱道建,皮晓珊,岳显昌,等. 天地波雷达回波的直达波抑制[J]. 中国电子科学研究院学报, 2017,12(1):31-36.

[2] 张朕滔. 高频天地波雷达海杂波锐化及目标检测[D]. 哈尔滨: 哈尔滨工业大学, 2015.

[3] 刘斌,吴雄斌,徐全军,等. 分布式高频地波雷达阵列幅相误差的校准方法[J]. 武汉大学学报(理学版), 2012, 58(3):269-274.

[4] 曹圣红. 存在阵列误差条件下波达方向估计算法研究[D]. 合肥: 中国科学技术大学, 2014.

[5] 王敏,马晓川,鄢社锋,等. 阵列幅度/相位误差的有源校正新方法[J]. 信号处理, 2015, 31(11):1389-1395.

[6] 龙超,吴雄斌,柯亨玉,等. 多频率高频地波雷达的阵列幅相校正[J]. 华中科技大学学报(自然科学版), 2012, 40(5):97-101.

[7] 杨光. DOA估计中阵列幅相误差校正算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.

[8] 王永良,陈辉,彭应宁,等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004:430-434.

[9] 李磊,李国林. 通道幅相误差条件下的相干信源波达方向估计[J]. 系统工程与电子技术，2015，37(10)：2222-2227.

[10] 刘春波,陈伯孝,陈多芳,等. 双基地高频地波SIAR通道幅相误差的自校准方法[J]. 电子与信息学报，2009,31(3):614-618.

[11] 刘斌. 分布式高频地波雷达阵列误差有源校准[D]. 武汉: 武汉大学, 2012.

[12] ZHANG L, WU X, LIU J, et al. Multi-Frequency High Frequency Surface Wave Radar Based on Phase Offset[J].IET Radar, Sonar & Navigation,2015,9(8):1106-1111.