采样定时偏差对无源雷达性能影响研究
, , ,2, ,
(1.武汉大学电子信息学院, 湖北武汉 430072;2.中国洛阳电子装备试验中心, 河南洛阳 471000)
0 引言
无源雷达,即外辐射源雷达[1],是被动接收并利用空间已存在的非合作电磁波作为照射源来进行目标探测的双(多)基地雷达系统[2]。相比于传统雷达而言,外辐射源雷达具有很多优势:1)无需频率分配,不发射电磁波,有很好的“四抗”能力[3];2)不易被地方摧毁,生命力较强;3)研制和维护成本低、设备体积小、机动性强、易于部署。
正交频分复用[4](Orthogonal Frequency Divi-sion Multiplexing,OFDM)技术作为一种多载波调制的改进方案,利用并行数据传输技术,能够有效抑制多径传输所造成码间干扰,避免了高复杂度的信道均衡,同时有着频谱利用率高、成本低等优点。
目前已被研究用来作为外辐射源雷达非合作照射源的OFDM波形数字信号包括:DAB(数字音频广播)、DVB-T(数字视频广播)、DTMB(数字地面电视)、CMMB(中国数字移动多媒体视频广播)、WiFi信号、移动通信信号等[5-12]。
OFDM波形外辐射源雷达通常设有两个通道:参考通道和监测通道,分别用来接收参考信号和监测信号。通过监测信号与参考信号的匹配滤波以提取目标的距离和多普勒信息。实际处理中面临的主要问题包括:参考通道信号中不可避免地存在多径和噪声污染,参考通道信号需要进行重构提纯参考信号[13-14]。另一方面,监测通道信号中往往存在直达波和多径回波,使得匹配滤波后的目标信号在距离多普勒谱上被掩盖,直达波和多径杂波抑制也是需要解决的问题[15-20]。
在信号重构过程中,由于时间同步或载波频偏估计不准确等因素,会导致重构后参考信号和监测信号相关性下降,对雷达探测性能产生影响。文献[21]分析了无源相干脉冲雷达系统中,由于时间同步误差对系统相参检测和多普勒频率估计的影响。文献[22]分析了载波频偏估计误差对OFDM外辐射源雷达系统性能的影响,参考信号重构误码率、时域杂波抑制性能、目标速度估计精度等均会受其影响。由于采样定时偏差在解调过程中带来的影响可通过均衡技术很好地修正,并不需要额外的补偿器,所以采样定时偏差往往不容易引起关注。然而采样定时偏差对OFDM外辐射源雷达系统性能却会带来一定的影响,这方面还没有明确的研究。本文通过理论分析,分别讨论采样定时偏差对参考信号重构、相关系数、时域杂波抑制和匹配接收性能的影响,基于WiFi信号帧结构的特点,提出了一种对采样定时偏差估计和补偿的方法,通过WiFi外辐射源雷达实测数据加以验证。
1 系统模型
采样定时偏差,也叫采样时钟的相位偏差。当发射机和接收机中的采样速率或频率完全一致时,会发生相位偏差。当存在相位偏差时,发射机和接收机的采样时间不一致。在这种情况下,接收机的采样时刻与最佳采样时刻之间存在某个固定的时间差[23],如图1所示。
图2所示的是OFDM外辐射源雷达信号处理流程。首先利用参考通道信号估计出载波频偏,并对信号重构得到纯净的参考信号,将监测通道信号补偿载波频偏之后进行直达波和多径杂波的抑制,利用重构后的参考信号和杂波抑制以后的监测信号作二维互相关,得到匹配滤波的结果,再进行目标检测和跟踪。下面依次讨论采样定时偏差对参考信号重构、相关系数、时域杂波抑制和匹配接收性能的影响。
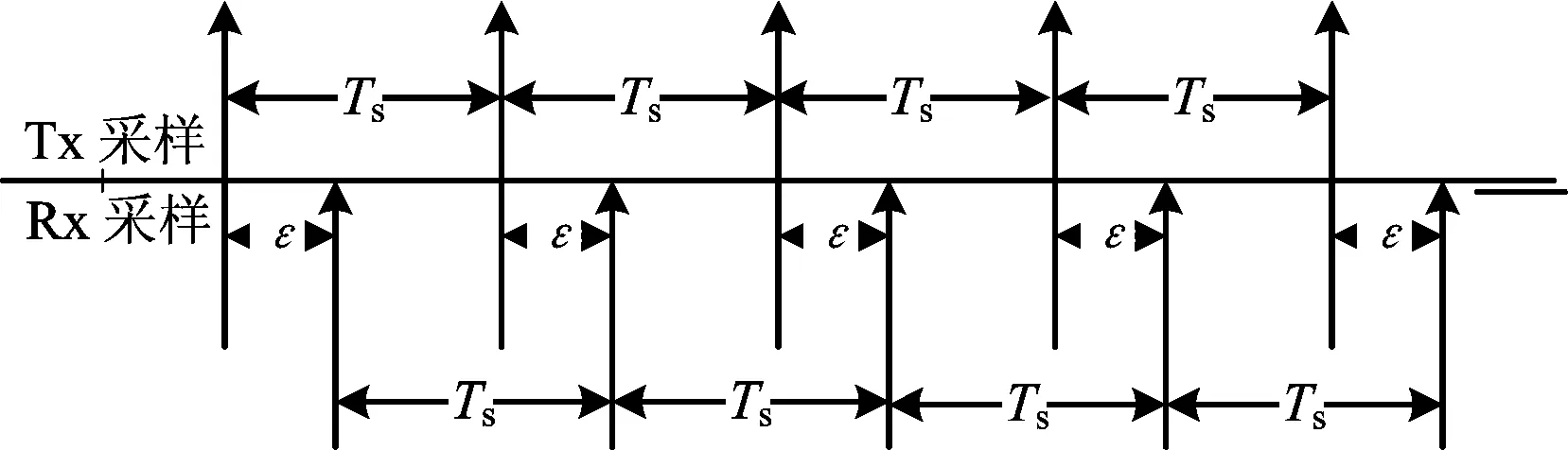
图1 采样定时偏差示例
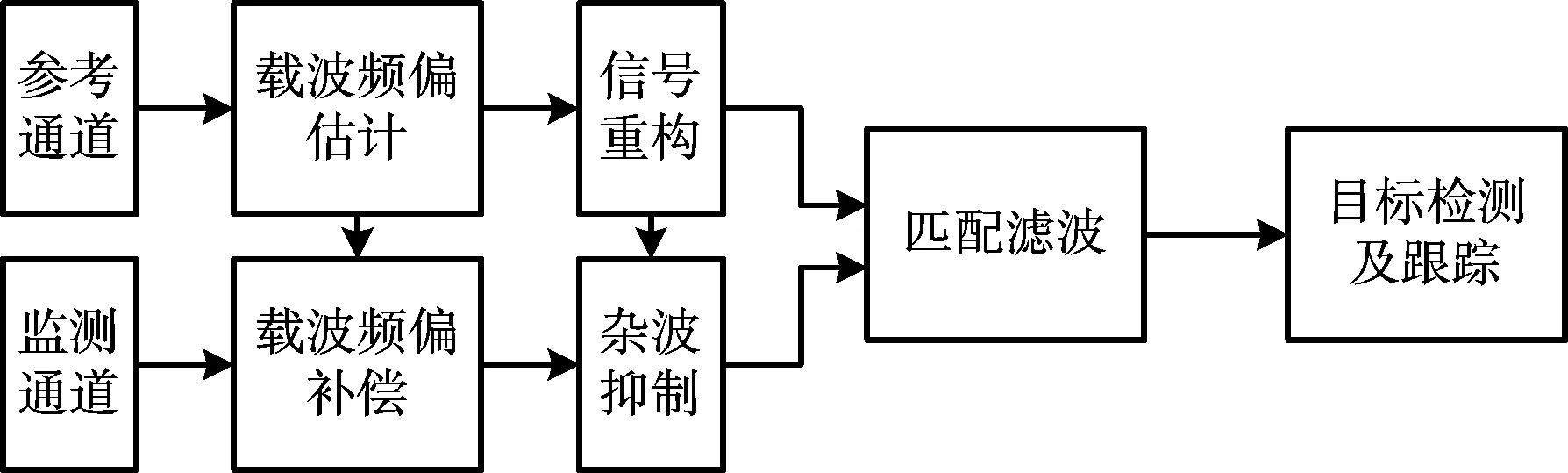
图2 OFDM外辐射源雷达信号处理流程
2 采样定时偏差对重构的影响
OFDM基带表达式[24]为
(1)
式中,s(t)为数模转换后的模拟信号,ck为串行发送的数据流,k为子载波序号,N为子载波数,fk=k·Δf,Δf=1/NTs,Ts为发送符号的采样间隔,T=NTs为OFDM符号的持续时间。
由于发射机和接收机的参考时钟不一致,接收机的采样时刻与最佳采样时刻之间存在某个固定的时间差,即采样定时偏差。在这里,令采样定时偏差为Δt,其中-0.5Ts<Δt<0.5Ts,则接收端的信号如式(2)所示,其中t=0,Ts,2Ts,…,(N-1)Ts,Δt为正代表接收端采样点在最佳采样点之后,Δt为负代表接收端采样点在最佳采样点之前。
(2)
作傅里叶变换,得到FFT解调信号:
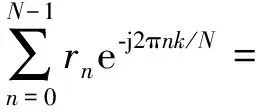
ckej2πkΔt/NTs
(3)
可见采样定时偏差引起符号相位旋转,k值越大,相位旋转越大。但在OFDM解调过程中,通过信道均衡技术可以很好补偿回来[23]。下面给出存在采样定时偏差时接收信号均衡前后的星座图,如图3所示。
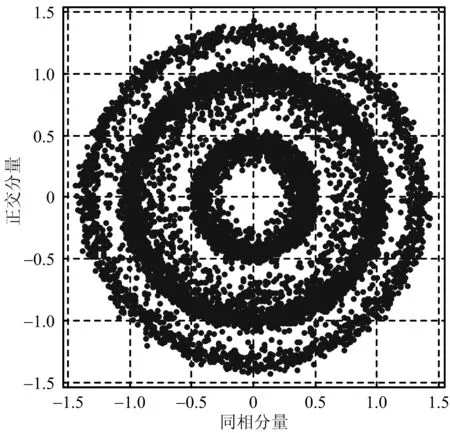
(a) 均衡前星座图
3 采样定时偏差对相关系数的影响
参考图2的OFDM外辐射源雷达信号处理流程,这里认为准确地估计出了载波频偏,在参考通道和监测通道中对数据作了补偿。采样定时偏差对符号产生了相位旋转,在参考信号重构时,通过均衡技术对参考通道的数据作了补偿,但是监测通道的数据并没有得到补偿,监测通道中存在大量的直达波信号,这样会使重构后的参考信号和监测信号的相关性减弱。
下面推导OFDM符号的自相关系数和采样定时偏差的关系,对于单个符号而言,自相关函数为
(4)
自相关系数为
(5)
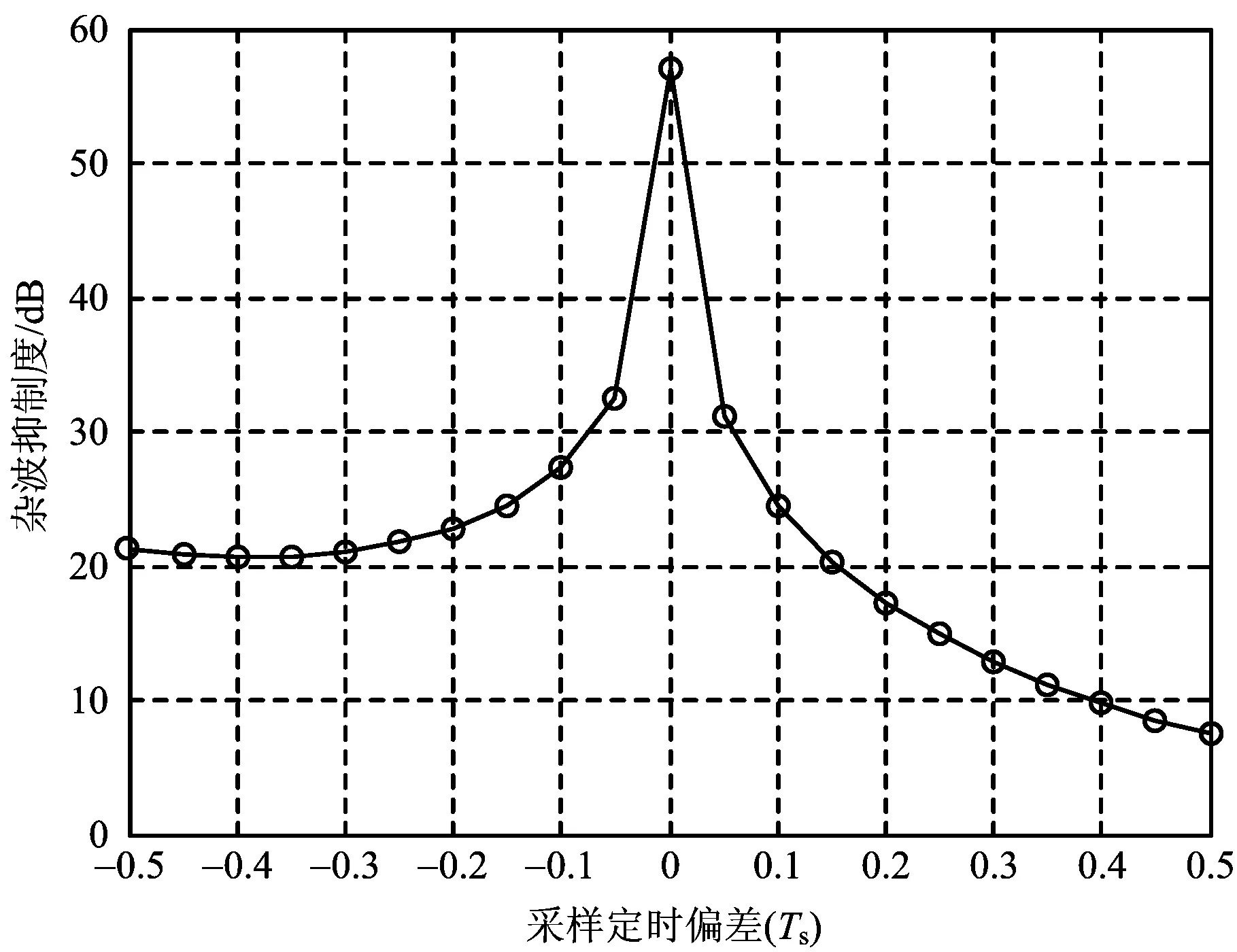
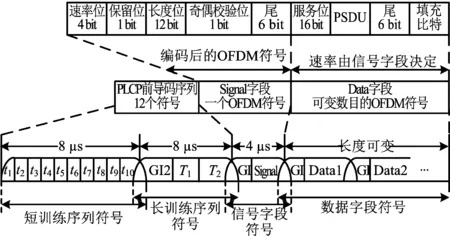
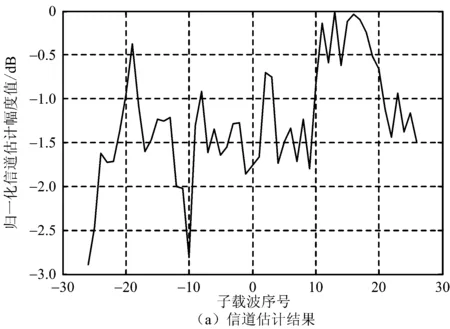
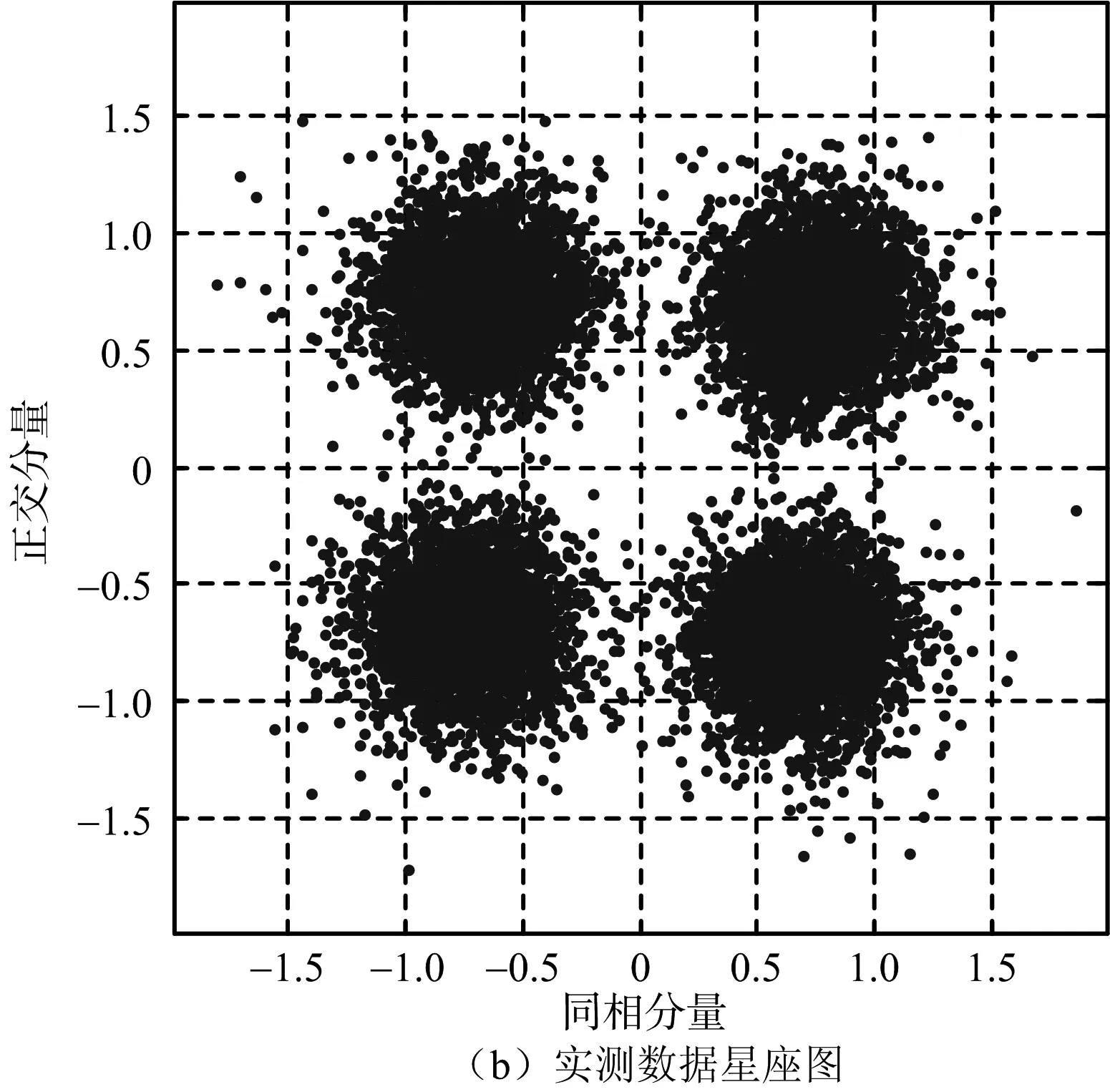
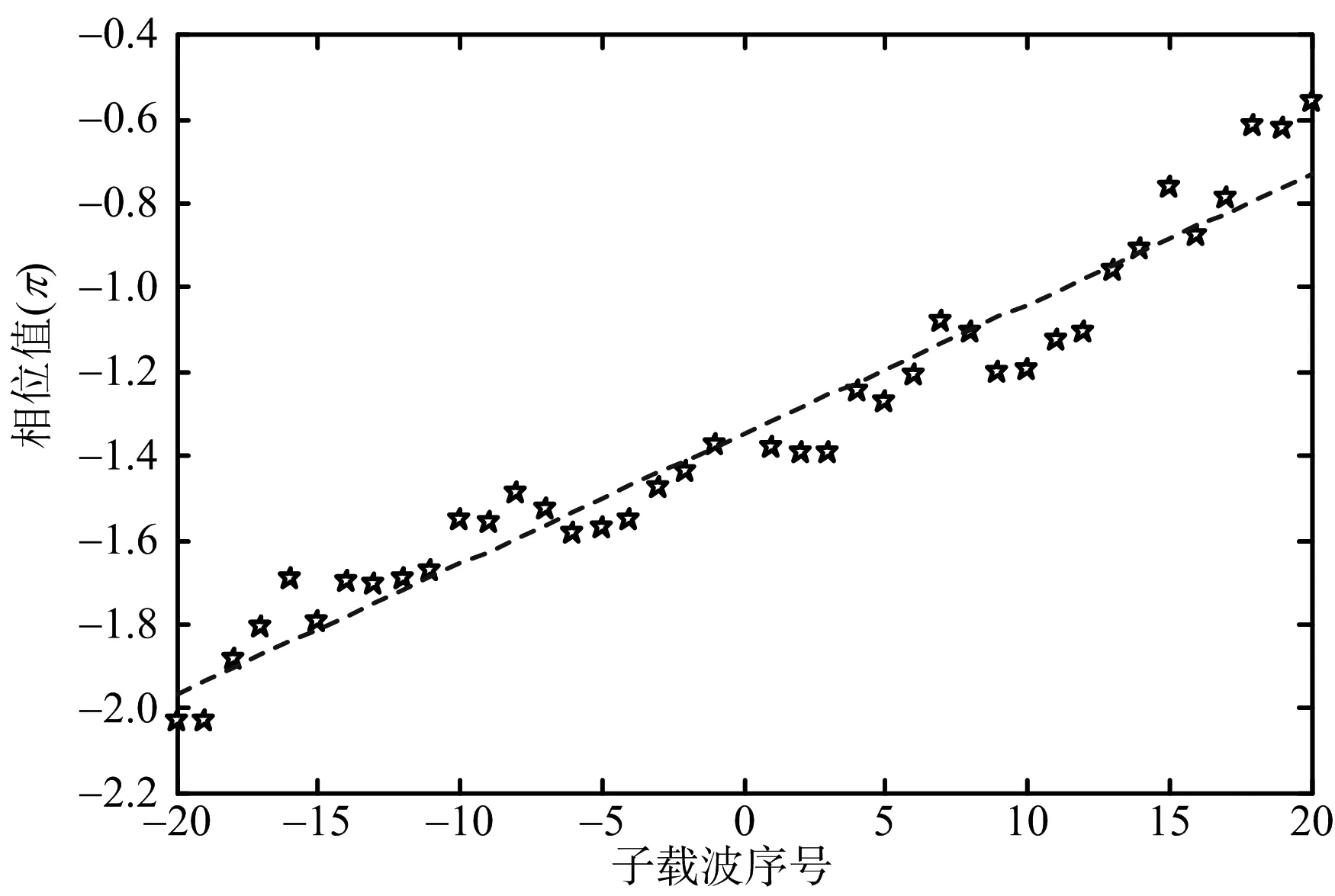
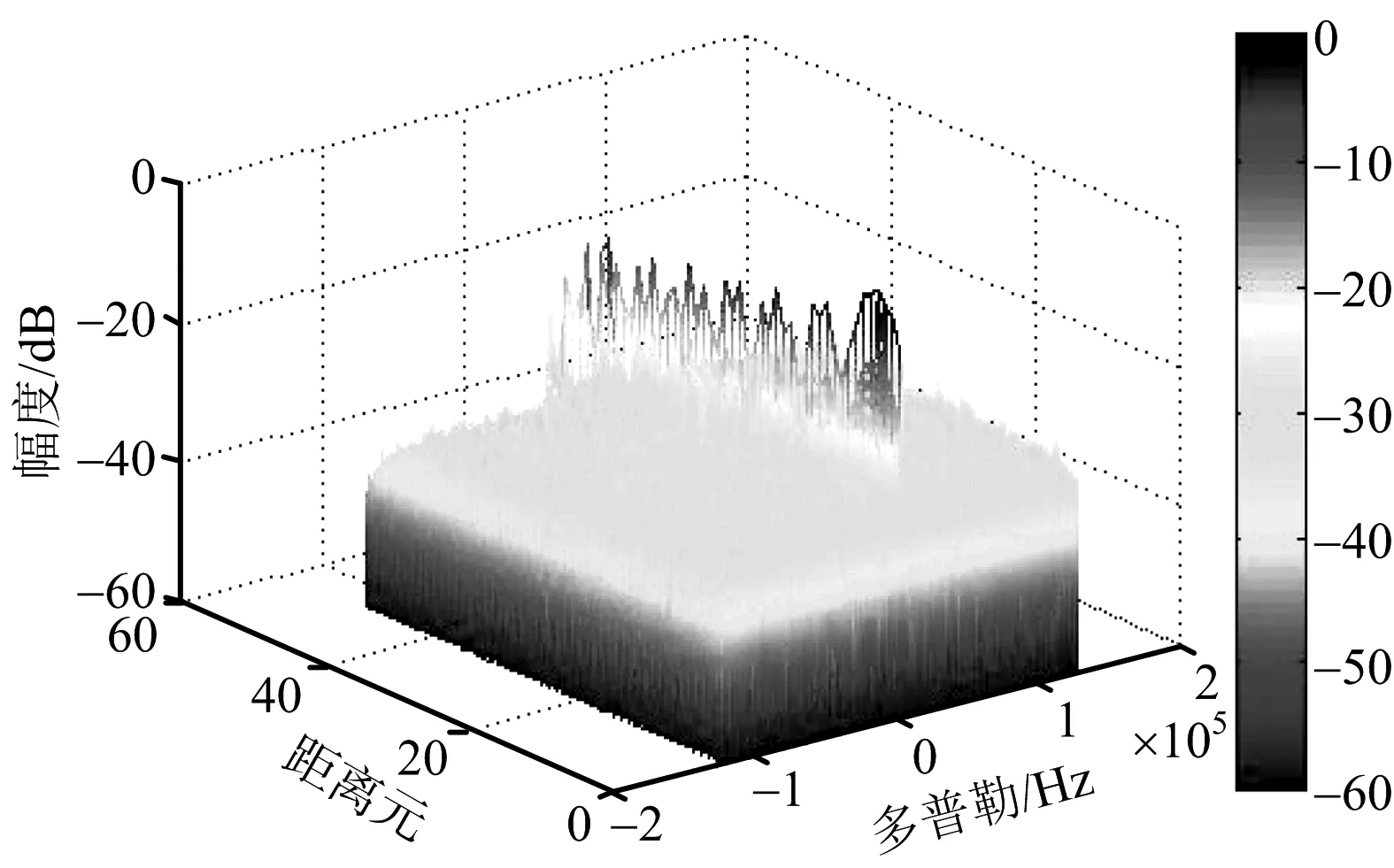
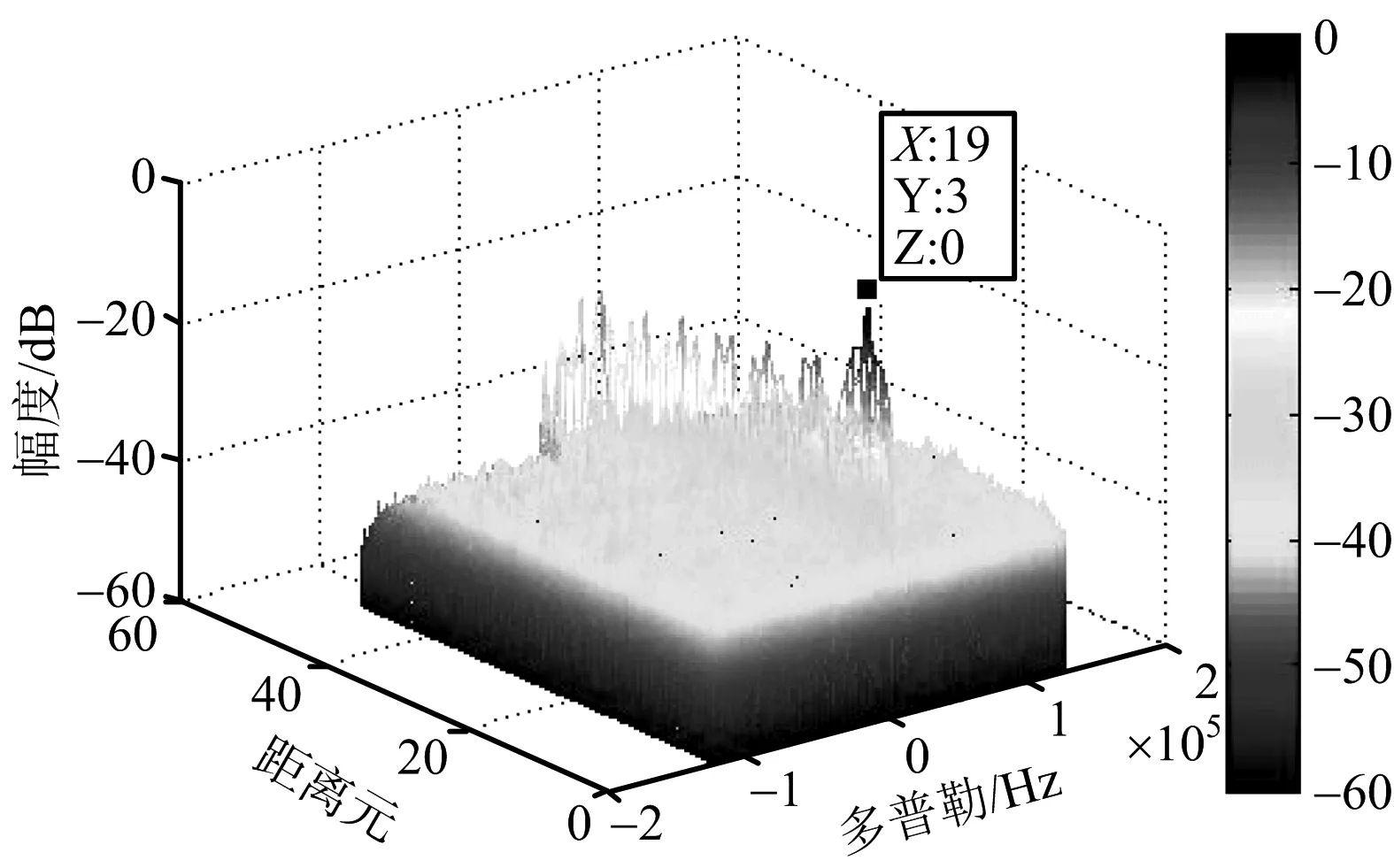
令Δt=xTs,其中-0.5 (6) 所以 (7) (8) N对自相关的值基本没有影响,即相关系数的值取决于定时偏差,和子载波数没有关系,如图4所示。 图4 OFDM自相关系数和采样定时偏差的关系 前文分析了采样定时偏差对自相关系数的影响,若参考通道信号和监测通道信号相关性不高,时域杂波抑制的性能会大受影响。下面分析采样定时偏差对时域杂波抑制的影响,监测通道中时域杂波抑制后(以ECA算法[25]为例)的输出信号为 (9) 式中,ssurv(i)为监测通道在瞬时时刻ti=iTs,i=0,…,N-1采集到的信号样本,用向量可以表示为 ssurv=[ssurv(0),ssurv(1),ssurv(2),…,ssurv(N-1)]T (10) sref(i)为参考通道所采集的N+M-1个信号样本重构后的值,用向量表示为 sref=[sref(-M+1),…,sref(0),…,sref(N-1)]T (11) wk为自适应滤波器权值系数,用向量表示为 W=[w0,w1,…,wM-1]T (12) 权值系数由求解代价函数得到 (13) 式中: (14) 当积累时间较长,为了提高算法性能,可对ECA算法进行扩展得到ECA_B算法。将原本的样本分块,分块数为b,则分块后,每块的采样点数为NB=N/b,此时,ssurv和sref被以下公式替换: ssurv=[ssurv(iNB),ssurv(iNB+1),…, ssurv((i+1)NB-1)]T (15) sref=[sref(iNB-M+1),sref(iNB-M),…, sref((i+1)NB-1)]T (16) 相应地,其杂波空间矩阵为 (17) (18) 最后的输出信号为 sECA_B=[sECA_B0,sECA_B1,…,sECA_Bb-1]T (19) 定义杂波抑制度为 (20) 式中,Px和Py分别为杂波抑制前后监测通道信号功率。 现假定监测通道中只存在直达波和目标回波,仿真参数设置为直达波信噪比60 dB,WiFi信号速率为24 Mbit/s,对应的调制方式为16 QAM,单目标距离元20,多普勒频移为200 Hz,目标信噪比为0 dB,积累时间为0.5 s,采用ECA_B算法,采样定时偏差设置从-0.5Ts到0.5Ts。仿真结果如图5所示,监测通道直达波的抑制程度受采样定时偏差的影响非常大,仅存在0.1Ts的采样定时偏差时,杂波抑制度便在30 dB以下。采样定时偏差为负时的杂波抑制度要好于采样定时偏差为正时的杂波抑制度,且随着采样定时偏差的增大,最后杂波抑制度会稳定在20 dB左右。 图5 采样定时偏差对杂波抑制度的影响 参考信号和目标回波信号的互模糊函数[26]定义为 (21) 式中,s(t)为参考信号,v(t)为回波信号,τ为时延,fd为多普勒频移,T为信号积累时间。为了便于分析,令回波信号v(t)=s(t-τ0)ej2πfd0t,其中τ0和fd0为目标实际的时延和多普勒频移,积累时间取一个OFDM符号持续时间,则互模糊函数为 ejπ(fk1-fk2+fd-fd0)T· sinc[π(fk1-fk2+fd-fd0)T]= ejπ[Δk+(fd-fd0)NTs]· sinc{π[Δk+(fd-fd0)NTs]} (22) 在这里,只考虑互模糊函数的模,令 f(τ,fd,k,Δk)= sinc{π[Δk+(fd-fd0)NTs]} (23) 则 (24) 当τ=τ0,fd=fd0时,|χ(τ,fd)|取得最大值。 同理,当存在采样率定时偏差时: (25) 同样地,令Δt=xTs,则式(25)表示为 (26) 采样率定时偏差会对互模糊函数的结果造成影响,互模糊函数匹配出目标在τ=τ0,fd=fd0,如果存在0.5Ts的采样定时偏差,会使目标的信噪比下降2 dB左右,这种情况下会使目标探测性能急剧下降。 由于前文分析的采样定时偏差会对时域杂波抑制和互模糊函数匹配峰值带来影响,所以对采样定时偏差的估计和补偿非常重要。在这里可利用重构过程中的已知信息对采样定时偏差进行估计。 IEEE 802.11g协议的OFDM模式下,WiFi信号每一帧的帧头有两个符号的长训练序列用于信道估计,以及每一个OFDM符号中有4个导频用于剩余相位跟踪,信号帧结构如图6所示,导频位置如图7所示。当各个子载波归一化信道估计结果幅度值大小差别超过3 dB时,认为信号受信道影响较大,不适于用来估计采样定时偏差;当其大小差别在3 dB之内时,可利用各个子载波信道估计结果相位值来估计采样定时偏差。 图6 WiFi信号帧结构 图7 导频位置示意图 解调过程中,信号在作信道估计之前会利用帧头的短训练序列和长训练序列作两次载波频偏估计和补偿。考虑到实际过程中,载波频偏经过补偿之后,仍会有部分残余频偏的存在,频偏的存在会影响信号的相位值,这部分频偏需要利用每个OFDM符号中4个已知的导频来修正。 利用文献[27]中导频估计残余频偏带来相位值的方法,对每个符号取平均,得到相位值Φ2。将各个子载波信道估计结果相位值Φ1减去这一部分估计出来的残余频偏相位值,得到Φ3=Φ1-Φ2,此时可认为剩余的相位全部都是由采样定时偏差带来的。 由式(3)可知,采样定时偏差带来的子载波的相位旋转值为 (27) (28) 对于WiFi信号,式中N=64。得到定时偏差的估计值以后,可通过内插的办法纠正监测通道信号。 本文实测分析选用了2015年6月武汉大学电波传播实验室进行的WiFi外辐射源雷达实验数据。实验信号为802.11 g的OFDM模式下的WiFi信号,选用的信道为2信道,载波频率为2 417 MHz,接收端采样频率为20 MS/s。 图8 实测数据解调结果 图9 剩余相位一次曲线拟合结果 (a) 采样定时偏差补偿前 (b) 采样定时偏差补偿后图10 监测通道数据补偿采样定时偏差前后结果图 将估计出的采样定时偏差值,用内插的方法对监测通道数据进行补偿。图10给出了补偿前后对监测通道数据进行杂波抑制后的结果图。杂波抑制算法选用ECA_B算法,抑制阶数为40个距离元,积累时间为1 s。可以发现,补偿前后零多普勒附近都存在一些剩余的直达波和多径杂波,补偿前看不到目标的匹配尖峰,但在补偿后目标的尖峰凸显,且杂波抑制度提升了6.5 dB左右,匹配出的目标也符合实验场景,实验中,人在较小的范围内以较低的速度运动。 由于采样定时偏差的估计存在一定的误差,且实际环境中还存在着很多其他因素的干扰,在对监测通道数据进行补偿后,并不能得到仿真结果中接近30 dB的杂波抑制度的提升,但此方法在一定程度上提高了雷达系统的探测性能。 本文分析了采样定时偏差对OFDM外辐射源雷达探测性能的影响。理论分析和仿真可知,采样定时偏差会对子载波产生相位旋转,参考信号重构过程中,均衡技术可纠正这个影响。但这样会使参考信号和监测信号的相关性减弱,大大影响了时域杂波抑制的性能,并且互模糊函数匹配出的目标信噪比也会降低。可利用重构过程中的已知信息对采样定时偏差进行估计,并利用内插的方式对监测通道数据进行补偿,这种方法的有效性在实测数据中得到验证,在一定程度上提高了雷达系统的探测性能。 [1] 万显荣. 基于低频段数字广播电视信号的外辐射源雷达发展现状与趋势[J]. 雷达学报, 2012, 1(2):109-123. [2] KUSHEL H, O’HAGAN D. Passive Radar from History to Future[C]∥11th International Radar Symposium, Vilnius, Lithuania: IEEE, 2010:1-4. [3] 金威,吕晓德,向茂生. 基于DVB-S信号的外辐射源雷达的模糊函数及分辨特性分析[J]. 雷达学报, 2012, 1(4):380-386. [4] 霍凯,赵晶晶. OFDM新体制雷达研究现状与发展趋势[J]. 电子与信息学报, 2015, 37(11):2776-2789. [5] CAPRIA A, PETRI D, MARTORELLA M, et al. DVB -T Passive Radar for Vehicles Detection in Urban Environment[C]∥IEEE International on Geoscience and Remote Sensing Symposium, Honolulu, Hawaii: IEEE, 2010:3917-3920. [6] COLEMAN C, YARDLEY H. Passive Bistatic Radar Based on Target Illuminations by Digital Audio Broadcasting[J]. IET Radar, Sonar & Navigation, 2008, 2(5):366-375. [7] 万显荣,孙绪望,易建新,等. 分布式数字广播电视外辐射源雷达系统同步设计与测试[J]. 雷达学报, 2017, 6(1):65-72. [8] 万显荣,岑博,易建新,等. 中国移动多媒体广播外辐射源雷达参考信号获取方法研究[J]. 电子与信息学报, 2012, 34(2):338-343. [9] 万显荣,邵启红,夏鹏,等. 数字地面多媒体广播外辐射源雷达微多普勒效应实验[J]. 系统工程与电子技术, 2016, 38(11):2499-2504. [10] 王慧,洪丽娜,易建新,等. 数字外辐射源雷达目标徙动补偿新方法[J]. 电子与信息学报, 2015, 37(5):1017-1022. [11] 饶云华,朱逢园,张修志,等. WiFi外辐射源雷达信号模糊函数及副峰抑制分析[J]. 雷达学报, 2012, 1(3):225-231. [12] 黄威振. 基于4G基站信号的被动雷达相关技术研究[D]. 成都: 电子科技大学, 2016. [13] 饶云华,明燕珍,林静,等. WiFi外辐射源雷达参考信号重构及其对探测性能影响研究[J]. 雷达学报, 2016, 5(3):284-292. [14] 万显荣,程熠瑶,易建新,等. DTMB外辐射源雷达参考信号重构信道估计新方法[J]. 电子与信息学报, 2017, 39(5):1044-1050. [15] REZNICEK M, BEZOUSEK P, SHEJBAL T. Clutter Suppression in Passive Coherent Radar Systems[C]∥International Symposium ELMAR, Zadar, Croatia: IEEE, 2016:151-154. [16] GARRY J L, SMITH G E, BAKER C J. Direct Signal Suppression Schemes for Passive Radar[C]∥Signal Processing Symposium, Debe, Poland: IEEE, 2015:1-5. [17] 杜超. 数字电视外辐射源雷达干扰抑制和微弱目标检测技术研究[D]. 北京: 北京理工大学, 2015. [18] 张坚,万显荣,刘玉琪. 外辐射源雷达滑窗扩展相消算法并行实现[J]. 雷达科学与技术, 2017, 15(2):115-125. ZHANG Jian, WAN Xianrong, LIU Yuqi. Parallel Implementation of Sliding Extensive Cancellation Algorithm for Passive Radar System[J]. Radar Science and Technology, 2017,15(2):115-125.(in Chinese) [19] 翟永惠,吴江,王鼎. 采用时延估计的外辐射源雷达杂波抑制算法[J]. 西安交通大学学报, 2015, 49(12):47-52. [20] 张曙泽. 基于空域和极化域的数字电视外辐射源雷达干扰抑制研究[D]. 北京: 北京理工大学, 2015. [21] 何友,张财生,丁家会,等. 无源相干脉冲雷达时间同步误差影响分析[J]. 中国科学:信息科学, 2011, 41(6):749-760. [22] 赵志欣,万显荣,谢锐,等. 载波频偏对正交频分复用波形外辐射源雷达性能影响的研究[J]. 电子与信息学报, 2013, 35(4):871-876. [23] CHO Y S, KIM J, YANG W Y, et al. MIMO-OFDM无线通信技术及MATLAB实现[M]. 孙锴,黄威,译. 北京: 电子工业出版社, 2013:150-151. [24] 李平,赵志辉,张振仁. 采样时钟偏差对OFDM系统性能的影响[J]. 信息与电子工程, 2006, 4(16):431-435. [25] 卢岑. 基于WiFi的外辐射源雷达杂波抑制及匹配滤波研究[D]. 武汉: 武汉大学, 2014. [26] 唐波,程水英,张浩. 外辐射源雷达模糊函数副峰抑制算法研究[J]. 电子学报, 2015,43(6):1058-1064. [27] 史治国,洪少华,陈抗生. 基于XILINX FPGA的OFDM通信系统基带设计[M]. 杭州: 浙江大学出版社, 2009:165-166.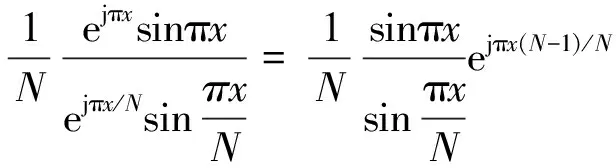
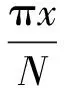

4 采样定时偏差对时域杂波抑制的影响

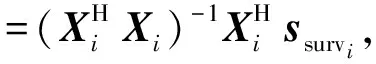
5 采样定时偏差对匹配接收性能的影响
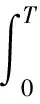


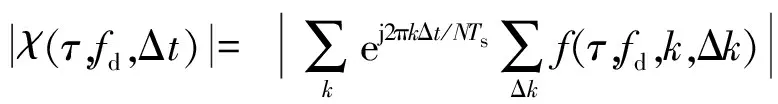
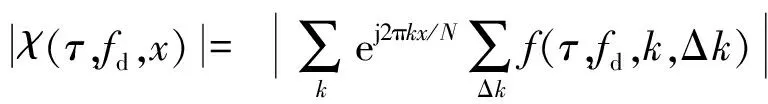
6 对采样定时偏差的估计和补偿


7 实测数据分析
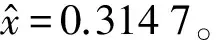
8 结束语

