基于方位散射熵的建筑物特征提取方法

， ，

(桂林电子科技大学信息与通信学院， 广西桂林 541004)

0 引言

穿墙感知技术具有广泛的应用场景，基于电磁波穿透原理的穿墙雷达成像(TWRI)是进行穿墙感知的有效手段[1-8]。现阶段的TWRI主要用于墙体成像，当建筑物结构复杂、墙体层数较多时，墙体成像不完整、不清晰，难以得到高质量的建筑物布局图像。而通过TWRI得到建筑物主要散射中心，由图理论方法[2]进行布局重构即可得到完整清晰的建筑物布局。

目前，在建筑物角散射中心提取方向已有研究人员作了相关研究。文献[7]中利用了墙体和墙角在极化特性上的差异，采用交叉极化收发共置雷达识别建筑物墙角，但是交叉极化接收到的回波信号较弱，造成建筑物墙体成像中耦合信号过强、墙角成像模糊，此种算法没能充分利用建筑物的极化特性提取角散射体。文献[9-10]利用散射体在不同频率、不同子孔径中的散射特性，在特定测试角度确定散射体位置。尽管在合适的角度测试能避免墙体回波，减少散射体相关旁瓣，但在建筑物内部结构未知的情况下，不易确定适合的观测角度，墙角位置信息定位误差较大。文献[11-12]利用图像匹配滤波算法、过完备字典算法和相关匹配算法对建筑物成像得到散射体方位信息，但该方法未充分利用墙体和墙角的散射特性，造成建筑物内墙体信号强烈，墙角信号不易识别，位置信息定位不准确。

本文着重考虑散射体的极化特性与方位角属性，通过一种基于极化相关性和方位散射熵的建筑物角散射中心提取方法，以解决墙角弱信号被掩盖的问题。首先对回波数据采用后向投影算法得到建筑物原始图像，利用散射点交叉极化相关性对交叉极化成像结果进行加权提取墙角；然后观测散射点散射幅度随天线方位的变化规律，利用方位散射熵滤除墙体信息、增强墙角信息；最后采用中心定位法对初步定位的散射中心进行精确定位。该方法不仅能高效地检测出建筑物的角散射中心，而且滤除了大部分的自然噪声，其检测性能具有实用价值。

1 建筑布局角散射中心模型

如图1所示模型是由3个房间组成的简单布局的建筑物，墙体厚度为0.1 m，使用SIMO雷达工作模式，在建筑物距离向中间位置设置一个发射天线发射步进频信号，沿距离向设置N个接收天线获取场景信息。

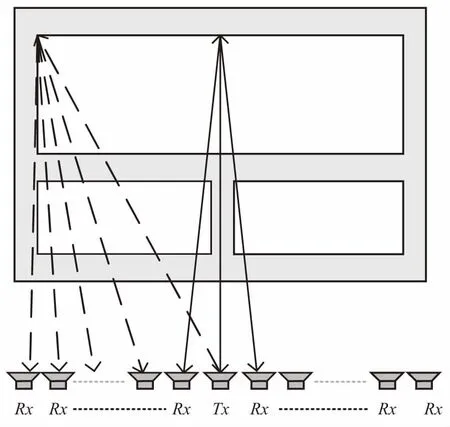
图1 建筑物布局图

根据几何绕射理论(Geometrical Theory Diffraction, GTD)和物理光学(Physical Optics, PO)理论，建筑物后向散射场近似为多个散射中心的叠加。考虑散射中心对方位角的依赖关系，第n个接收天线第m个频率接收到的场景信号[8]为

e-jωmτp,n+w(m,n)

(1)

将场景划分为Nx×Nz个像素点，Nx和Nz分别表示方位向和距离向的划分网格数。第(i,j)个像素点的坐标为(xi,yj)，对应的时延为τ(i,j),n，其像素值Ii,j表示接收到像素点(xi,yj)返回信号总和：

(2)

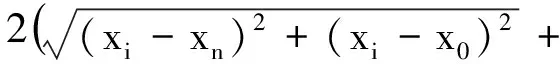
(3)

式中，时延τ(i,j),n表示从发射天线到像素点(xi,yj)再返回到第n个接收天线的时间，(x0,y0)和(xn,yn)分别表示发射天线和第n个接收天线的坐标。

2 角散射中心检测算法

在图1模型中，墙体在不同极化情况下散射特性不同，在同极化下，墙体和墙角信号明显；而交叉极化下，只有墙角和耦合信号明显[9]。同时，墙体、墙角的方位角属性区别较大，从而提出了一种角散射中心检测算法。通过角散射点的极化散射特性和方位属性提取并增强散射点，采用循环迭代的中心定位法计算得到精确的角散射中心位置信息，具体流程如图2所示。

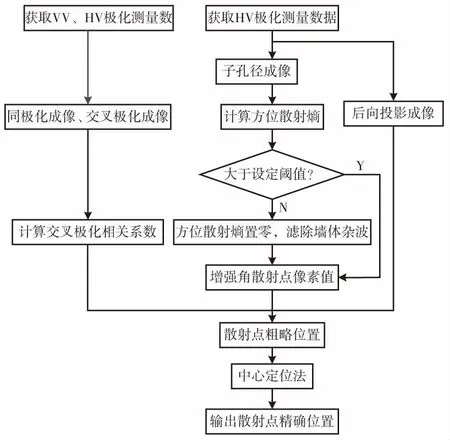
图2 角散射中心检测流程图

2.1 墙角信息增强

建筑物的强散射结构可由确定性的点散射模型来描述，墙角结构的确定性表现为散射在极化情况下具有的高度相关；与之相反，自然杂波因形状材质等不规则，其散射通常具有一定的随机性，墙体在不同极化情况下散射特性不同，因而它们的散射极化相关性较弱。最简单的极化相关性的提取根据极化类别可分为同极化(HH,VV)和交叉极化(HV，VH)两种情况。像素点(i,j)的全极散射幅度I(i,j)由同极化像素值IHH，IVV和交叉极化像素值IHV，IVH组成：

I(i,j)=I(i,j)HH+I(i,j)HV+I(i,j)VH+I(i,j)VV

(4)

像素点(i,j)的极化相关性ρ(i,j)k-l可利用同极化图像像素值IHH，IVV和交叉极化图像像素值IHV，IVH进行估计。k，l表示选取的极化类别，当k，l都选取同极化类别(HH，VV)时，ρHH-VV表示同极化相关性；当k选取同极化类别(HH，VV)，l选取交叉极化类别(HV，VH)时，ρHV-VH表示交叉极化相关性。

(5)

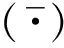
(6)

式中，I(i,j)HV为交叉极化成像得到的像素值，ρ(VV-HV)i,j为像素点加权因子。由于VV极化相对于HH极化具有更强的穿透力，墙体的VV-HV相关系数比HH-HV相关系数低，使用VV-HV相关系数可以充分利用散射体的极化特性，增强了墙角信息，能够更大幅度地削弱墙体信息和耦合信息，而且避免了交叉极化接收回波较弱的问题。虽然利用极化相关性削弱了墙体信息，但是场景成像中墙体信息不能被完全消除，对墙角位置信息的判断造成一定影响，进而引入方位散射熵消除墙体虚假像。

2.2 墙体虚假像滤波

绝大部分建筑物散射体的方位角主瓣宽度不同，特别是墙体、墙角的方位角主瓣宽度区别较大，主要散射体方位角属性可以被用来推测建筑物内部结构。由文献[9]可知，墙体的散射强度随方位视角变化呈现窄峰曲线，表明在不同方位视角下的墙体散射回波能量起伏明显；而墙角散射模型散射强度随方位角视角的变化比较缓慢，对于常见的矩形墙角或者三角形墙角，回波响应的波束宽度在方位向超过45°。

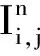
(7)

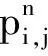
(8)

根据熵的定义，可给出方位不变特性的度量为

(9)

由于墙体和墙角对天线方位依赖性都比较大，本文采用非线性映射来增加墙体和墙角的区分度，定义E为方位散射熵：

Ei,j=(Mi,j)2

(10)

由于虚假像熵值较大，墙体的熵值比墙角熵值大，为了提取墙角，设置滤波门限T，滤波门限T的值应根据实际应用背景进行取值，T的一般值为0.2～0.5，所以阈值为场景最大方位散射熵值maxEi,j的T倍。小于门限阈值的像素点被判为有效散射点，大于门限阈值的像素点被置零，直接滤出。

(11)

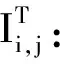
(12)

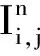
2.3 提取角散射点的精确位置

通过散射熵滤波可以确定角散射点的粗略位置，然后采用中心定位算法[13]来确定角散射点的精确位置信息，具体流程如图3所示。首先将图像二值化，进行膨胀和腐蚀，把位置相近的散射点连接起来；然后得到每个中心点的位置坐标，即

(13)

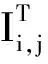
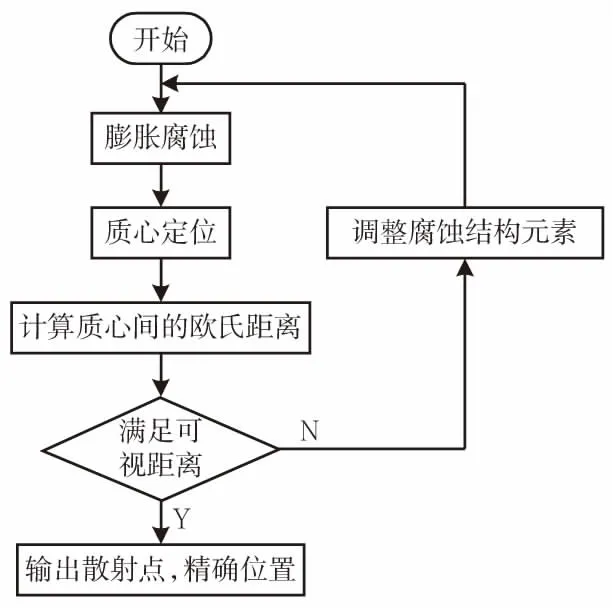
图3 中心定位法流程图

3 仿真与实验结果分析

3.1 仿真结果分析

仿真场景如图4所示，墙体厚度d和介电常数ε分别为0.1 m和4.5。在建筑物距离向中间位置设置一个发射天线，沿距离向设置21个接收天线。发射天线距离建筑物前墙2 m，位置为(2.0 m,1.0 m)，发射信号为超宽带脉冲信号，带宽为1 GHz；接收天线距离建筑物前墙2 m，起始位置位于(1.0 m,1.0 m)，截止位置位于(3.0 m,1.0 m)，相邻天线间距为0.1 m。对图4的回波进行墙体补偿的后向投影算法得到建筑物原始图像，利用散射体交叉极化相关性对HV 极化成像结果进行加权提取墙角，如图5所示；然后利用方位散射熵滤波算法滤除墙体信息、增强墙角信息，如图6所示，图中的黑色虚线表示建筑物角落的真实位置，可以看到提取的建筑物角散射点基本位于真实角落位置中；最后对图6进行膨胀和腐蚀，计算得到精确的散射点位置，如图7所示。图8为文献[7]的方法所得到的图像。

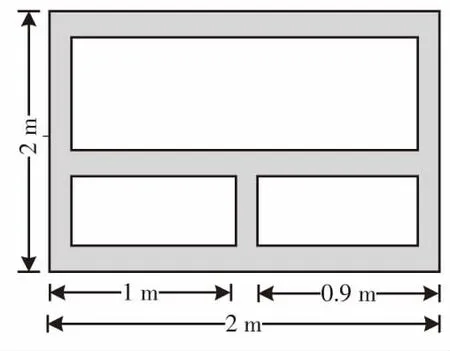
图4 仿真场景

图5 极化相关性方法成像图

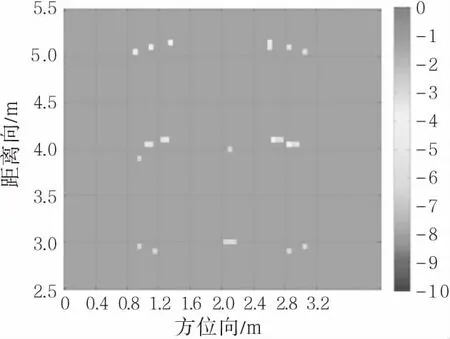
图6 方位散射熵方法成像

图7 精确确定角落位置

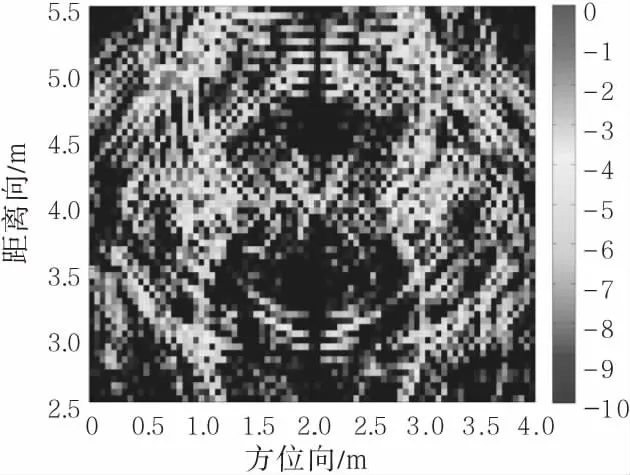
图8 文献[7]场景成像

从图中可以看出，使用本文所提出的算法，利用极化相关性可以强化墙角信息，同时可滤除大量耦合信号，由墙角与墙体的方位散射熵消除了大部分墙体信息，清晰精确地显示墙角位置，杂波相对较小，能够完整提取建筑物属性散射中心。

3.2 实验结果分析

为了验证本文算法在实际雷达测试数据中的重构效果，使用矢量网络分析仪器和喇叭天线构建了一套雷达测试系统，系统配置图和实测场景如图9所示，使用网络分析仪对一个长度为2 m的洗手台采集回波数据，图10是场景图像。安装在小车上的雷达天线由左向右形成1.8 m长的孔径，方位向采样间隔为0.3 m,雷达工作频率为1～2 GHz，起始频率为1 GHz，频率步进为10 MHz。

图9 实测场景

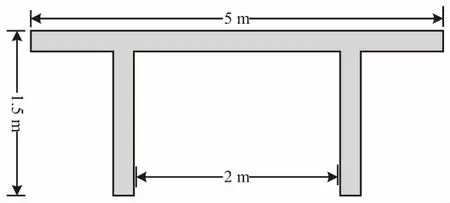
图10 场景图像

图11为文献[1]的方法所得到的图像，图12是使用本文算法得到的结果。从图中可以看出，文献[11]方法得到的图像存在大量耦合信号，墙角散射中心不易识别；使用本文所提出的算法，能充分利用墙角与墙体的方位属性，清晰精确地显示墙角位置，杂波相对较小，能够完整提取建筑物墙角散射中心。

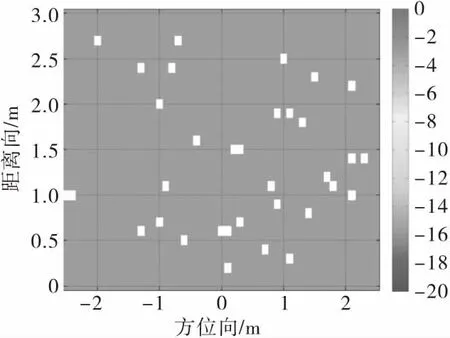
图11 文献[1]算法成像结果

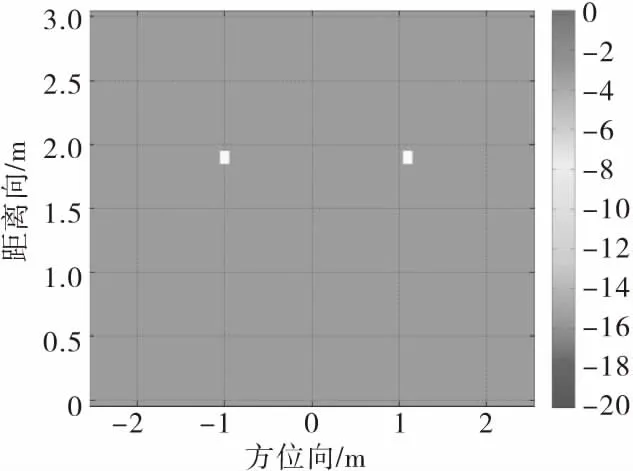
图12 本文算法成像结果

4 结束语

本文提出的基于极化相关性和方位散射熵的角散射中心提取方法，通过极化相关性检测出角散射点的位置信息，采用方位散射熵将方位依赖性较高的墙体滤除。一方面增强了墙角信息，消除了大量耦合信号，填补了墙角极化信息较弱的缺陷；另一方面大幅度消除墙体信息，抑制杂波及噪声，保证了角散射点位置信息的准确性。仿真数据验证和实测试验结果表明了该方法的有效性，能充分利用建筑物散射体的极化相关性和方位属性，有效增强角散射点信息，克服墙体杂波、耦合信号和噪声，完整提取建筑物角散射中心。

[1] BOUZERDOUM A, TANG V H, PHUNG S L. A Low-Rank and Jointly-Sparse Approach for Multipolarization Through-Wall Radar Imaging[C]∥ IEEE Radar Conference, Seattle,WA:IEEE,2017:263-268.

[2] LIU Jiangang, KONG Lingjiang, YANG Xiaobo, et al. Refraction Angle Approximation Algorithm for Wall Compensation in TWRI[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(7):943-946.

[3] YEKTAKHAH B, SARABANDI K. All-Directions Through-the-Wall Radar Imaging Using a Small Number of Moving Transceivers[J]. IEEE Trans on Geoscience and Remote Sensing,2016,54(11):6415-6428.

[4] JIA Yong, ZHONG Xiaoling, LIU Jiangang, et al. Single-Side Two-Location Spotlight Imaging for Building Based on MIMO Through-Wall-Radar[J]. Sensors, 2016,16(9):1441.

[5] LIU H, JIU B, LI F, et al. Attributed Scattering Center Extraction Algorithm Based on Sparse Representation with Dictionary Refinement[J]. IEEE Trans on Antennas and Propagation,2017,65(5):2604-2614.

[6] DE WIT J J M, VAN ROSSUM W L. Extraction of Building Features from Stand-Off Measured Through-Wall Radar Data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(1):149-158.

[7] CHEN Bo, JIN Tian, LU Biying, et al. Polarimetric Characteristics Analysis of Interior Structures of a Building in Through-the-Wall Radar Imaging[C]∥ IET International Radar Conference, Xi’an: IET, 2013:1-5.

[8] CHEN Bo, JIN Tian, ZHOU Zhimin, et al. Estimation of Pose Angle for Trihedral in Ultrawideband Virtual Aperture Radar[J]. Progress in Electromagnetics Research, 2013, 138(10):307-325.

[9] CHANG P C. Near Zone Radar Imaging and Feature Capture of Building Interiors[D].Columbus:The Ohio State University, 2008.

[10] CHANG P C, BURKHOLDER R J, VOLAKIS J L, et al. High-Frequency EM Characterization of Through-Wall Building Imaging[J]. IEEE Trans on Geoscience and Remote Sensing, 2009, 47(5):1375-1387.

[11] LAGUNAS E, AMIN M G, AHMAD F, et al. Determining Building Interior Structures Using Compressive Sensing[J]. Journal of Electronic Imaging, 2013, 22(2):381-388.

[12] LAGUNAS E, AMIN M G, AHMAD F, et al.Pattern Matching for Building Feature Extraction[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(12):2193-2197.

[13] 刘拥军,葛德彪,张忠治,等. 有属性的散射中心理论及应用[J]. 电波科学学报, 2003, 18(5):559-563.