基于序列时延相关性的PRI变换改进算法

，

(海军航空大学电子信息工程系， 山东烟台 264001)

0 引言

现代雷达侦察系统的主分选系统大多利用辐射源信号脉冲的到达时间(TOA)来估计脉冲重复间隔(PRI)，进而完成对辐射源的最终分选[1]。基于PRI的分选算法发展较为成熟，经典的算法有扩展关联法、直方图法(包括统计直方图法、累积差直方图法和序列差直方图法)以及PRI变换法。

以直方图法为代表的算法都是以计算脉冲到达时间的自相关函数为基础，因此极易出现“谐波”现象。同时，现实中侦察系统接收到的信号PRI调制类型复杂，包括参差、抖动、正弦调制、滑变等，直方图法对复杂调制PRI形式信号基本无能为力。PRI变换法可以完全抑制谐波的产生，同时对复杂PRI调制形式信号有较好的检测分选结果，但对参差PRI形式估计并不准确[2]。

以直方图法为代表的算法都是以计算脉冲到达时间的自相关函数为基础，因此极易出现“谐波”现象。同时，现实中侦察系统接收到的信号PRI调制类型复杂，包括参差、抖动、正弦调制、滑变等，直方图法对复杂调制PRI形式信号基本无能为力。PRI变换法可以完全抑制谐波的产生，同时对复杂PRI调制形式信号有较好的检测分选结果，但对参差PRI形式估计并不准确[2]。

针对PRI变换法存在的不足，文中引入脉冲序列时延自相关，对接收到的雷达辐射源信号脉冲序列进行整体时延变换。同时定义相关系数及对应的自相关函数，将自相关函数产生的峰值谱线引入PRI谱线图中配合分选。该算法结构简单，仿真实验验证了算法的实用性。

1 PRI变换

1.1 基本原理

文献[3]中介绍了PRI变换法及其相应的改进算法。

假设将脉冲前沿的时间记为脉冲的到达时间，即可以用表达式tn(n=0,1,2,…,N-1)表示待处理的脉冲序列的到达时间，N为要待处理脉冲的总数。当仅仅使用脉冲的TOA时，脉冲序列可以用单位冲击函数的和来表示：

(1)

其积分变换的形式即为PRI变换：

(2)

式中，τ=(tn-tm)>0为时间延迟，进一步可得

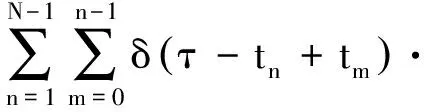
exp[2πit/(tn-tm)]

(3)

而自相关函数的定义为

(4)

通过比较可以发现，PRI变换与自相关函数极其相似，差别在于PRI变换中引入了一个相位因子exp(2πit/τ)，变换后其谐波分量采用的相位都是关于圆周对称的，因而完全消除了自相关函数引起的子谐波现象。

至于相位因子是如何抑制子谐波的产生，文献[4]有详细解释，此处不再赘述。

而针对传统PRI变换法无法对抖动PRI进行有效的检测和分选，同时克制由于引入相位因子而引起误差，后来的PRI变换法主要改进了以下两点：

1)设置可交叠的PRI箱；

2)设置可更新的起始时间。

改进后的PRI变换法可以通过设置上述两个参数达到有效分选抖动PRI的目的[4-5]。

1.2 算法不足

无论是传统PRI变换法还是经过改进的PRI变换法，都存在一个明显的缺点：对常规PRI和抖动PRI有效，但并不完全适用于参差PRI[6]。原因在于PRI变换采用变换箱来估计PRI的中心值，但参差PRI序列的子周期过于相近时，会出现“谐波抑制”的现象。

假设存在一个参差PRI序列，其骨干周期TC=T1+T2，从中可以得出

tT1=t+T1+nTC

(5)

tT2=t+nTC

(6)

通过PRI变换可得

exp[2πi(nTC+T1+t)/TC]}|=

(N-1)|1+exp(2πiT1/TC)|

(7)

从式(7)可以看出，当T1≈T/2以及|DT|≈0时，峰值并不出现在真实PRI处。通过PRI变换，两个参差PRI的子周期会被分别认为是单独的序列，峰值会出现在T1和T2处，而实际的T则被当作“谐波”抑制了。

同理，假设参差PRI脉冲序列中含有N个子周期，但其中任意N′个子周期之和近乎等于骨架周期的一半时，同样也会出现上述的情况。

针对上述问题，不同文献提出了相应的解决方法。

文献[7]以PRI变换为基础，对PRI谱线图进行双门限的设置。设置较小门限值来对参差PRI序列骨架周期进行检测，通过后期对检测到的PRI值进行组合比较最终确定参差PRI序列的骨架周期。

这种算法在参差PRI序列子周期大小并非十分相近的情况时能取得较好的效果。从图1的例子中可以看出，使用改进PRI变换法对二参差PRI脉冲序列分选，例如图1(a)中的情况，子周期大小差别很小时，骨架周期几乎是完全被“抑制”的(如图1(b))，根本无法通过门限检测出来，该算法并没有从本质上解决参差PRI序列的分选问题。

而文献[8-9]通过结合序列差值直方图(SDIF)和PRI变换法，分别利用各自算法针对不同PRI类型的分选优势来达到最终完整分选的良好效果。区别在于文献[8]中算法结合顺序为先SDIF再PRI变换法，而文献[9]中算法是先PRI变换法再SDIF。

两种算法有个共性问题有待商榷：由于采用顺序结构，后一个方法分选的正确程度过于依赖先前一个方法的分选结果。而SDIF在脉冲数较多且复杂的情况下针对参差PRI序列的分选并不理想。以SDIF为先的算法来说，图2是SDIF的分选效果图(其中脉冲序列包括常规PRI、参差PRI和抖动PRI形式，基本参数为常规PRI为217 μs，参差PRI子周期分别为74,83和95 μs，抖动PRI为220 μs，抖动程度为35)，从图中可以看出SDIF的分选效果并不理想(对参差PRI序列的骨架周期几乎没有准确检测)，进而会影响后续PRI变换法的分选。

图1 改进PRI变换法检测参差序列

图2 SDIF分选图

2 脉冲序列时延自相关

文献[7-9]中的方法之所以会暴露出一定的缺陷，一方面是因为它们并没有从本质上考虑参差PRI序列的特性，没有很好利用骨架周期的价值，另一方面也是由于其依托的基础——能够完全抑制谐波效应的PRI变换法，与参差PRI存在的问题是背道而驰的。因此，为寻求突破，应该跳出PRI变换法的基本框架[10]去寻求创新点。

本文为解决PRI变换法难以分选参差PRI序列的问题，特引入脉冲序列时延自相关的定义。

设接收到的脉冲序列为M,当仅考虑脉冲到达的时间，M可以表示为

M={t1,t2,…,tn}

(8)

接下来对全脉冲序列进行圆周时延处理：

将全脉冲列同时沿着时间轴线整体向后延迟一段时间，假设延迟时间为τ，则延迟后的序列可以表示为

Mτ={t1+τ,t2+τ,…,tn+τ}

(9)

再定义脉冲序列的时间匹配相关系数f(ti,tj):

(10)

根据设定的时间匹配相关系数定义脉冲序列的时延自相关函数：

k=1,2,…,n

(11)

式中,时延用脉冲间隔代替，即τ=tk-t1。

结合上述几个式子不难看出，定义的自相关函数会在时延为参差PRI序列的骨架周期时会出现峰值。

参差PRI序列时延示意图如图3所示。

从图中可以看出，对于参差PRI脉冲序列，通过时延自相关可以准确提取其骨架周期，结合PRI变换法便可以对参差PRI信号进行有效的分选。

同时，由于采用的是整体的时延变换，随着时延的增大，交叠的脉冲数会越来越少，峰值也会降低。因此，在不考虑脉冲丢失的情况下，可以通过参差PRI骨架周期的谐波自相关函数的峰值判断参差PRI序列子周期的个数。

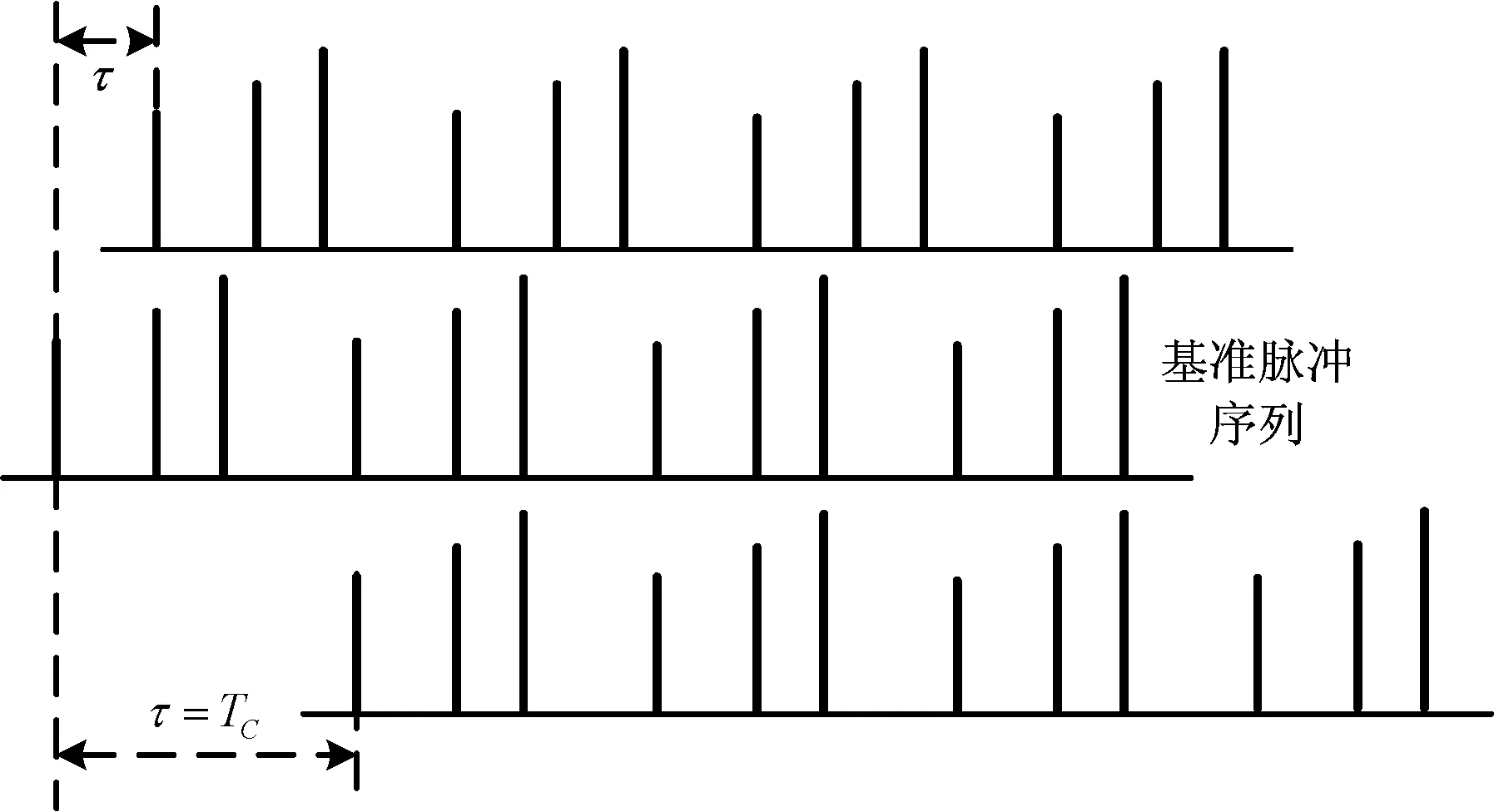
图3 参差PRI序列圆周时延自相关示意图

假定有一个m参差的序列，序列共有脉冲N个，骨架周期为Tg，则自相关函数峰值为

(12)

相邻峰值的差值为

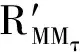
wm

(13)

式中，w为一个常数，与子周期数有关。

从上式可以看出，峰值的大小与参差PRI序列子周期的个数有密切的关系，因此通过比较其相邻谐波自相关函数峰值的差值即可得到子周期的个数。

不难发现，峰值也可能在另外两种情况下出现：

1)时延为常规PRI序列的一个或其谐波周期时；

2)时延为滑变PRI和正弦调制PRI的变化周期时。

通过这种自相关的运算希望得到的是参差PRI信号的相关信息，因此需要解决以下两个问题：

1)常规PRI周期及其谐波的影响

常规PRI信号也可以看作是单参差PRI序列，类似式(13)的分析，在经过序列时延自相关峰值谱图分析后，通过判断参差子周期的个数可以对常规PRI进行排除。

而为了突出本文算法对参差PRI序列的分选效果，鉴于大部分算法对常规PRI信号分选效果较好，本文此处采用未改进PRI算法对常规PRI信号进行检测抽取。

2)滑变PRI和正弦调制PRI变换周期的影响

以滑变PRI单调递增的情况为例，其模型为

(14)

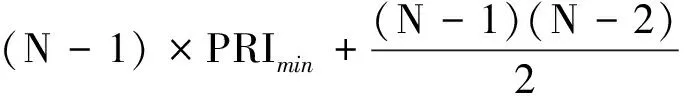
ΔPRI

(15)

式中，N为脉冲总数，ΔPRI为递增变量。

其PRI大小规律变换的周期Tfre显然要远远大于常规PRI序列的周期和参差PRI序列骨架周期，因此通过限定PRI周期的范围可以杜绝其产生峰值的影响。

滑变PRI和PRI正弦调制可以看成规律性的抖动PRI，因此可通过按照分选抖动PRI的方法进行分选，而分选后利用脉冲时延自相关可以提取的抖动脉冲序列进行PRI调制样式识别，进一步达到分离的目的。

3 算法具体流程

Step 1：首先利用序列差值直方图(SDIF)对雷达接收机接收到的脉冲序列进行初步估计，目的在于大略确定PRI的范围，以排除滑变PRI和正弦调制PRI变换周期的影响；

Step 2：利用未改进的PRI变换算法对常规PRI序列进行分选，排除影响；

Step 3：对全脉冲序列进行时延自相关运算，排除干扰信息的影响后，将峰值谱线以不同的颜色对应结合到PRI谱线图中；

Step 4：利用PRI变换算法对脉冲序列进行分选，生成PRI谱线图；

Step 5：对得到的完整谱线图进行比较分析后，确定PRI类型，对全脉冲序列进行序列搜索。

算法流程图如图4所示。

图4 算法流程图

4 仿真分析

为了充分验证本文对PRI变换法改进后的有效性，选取3种不同调制类型PRI的雷达辐射源信号脉冲进行仿真实验，辐射源信号参数如表1所示。待分选的脉冲序列由以下5部不同的雷达产生。

表1 雷达辐射源信号参数表

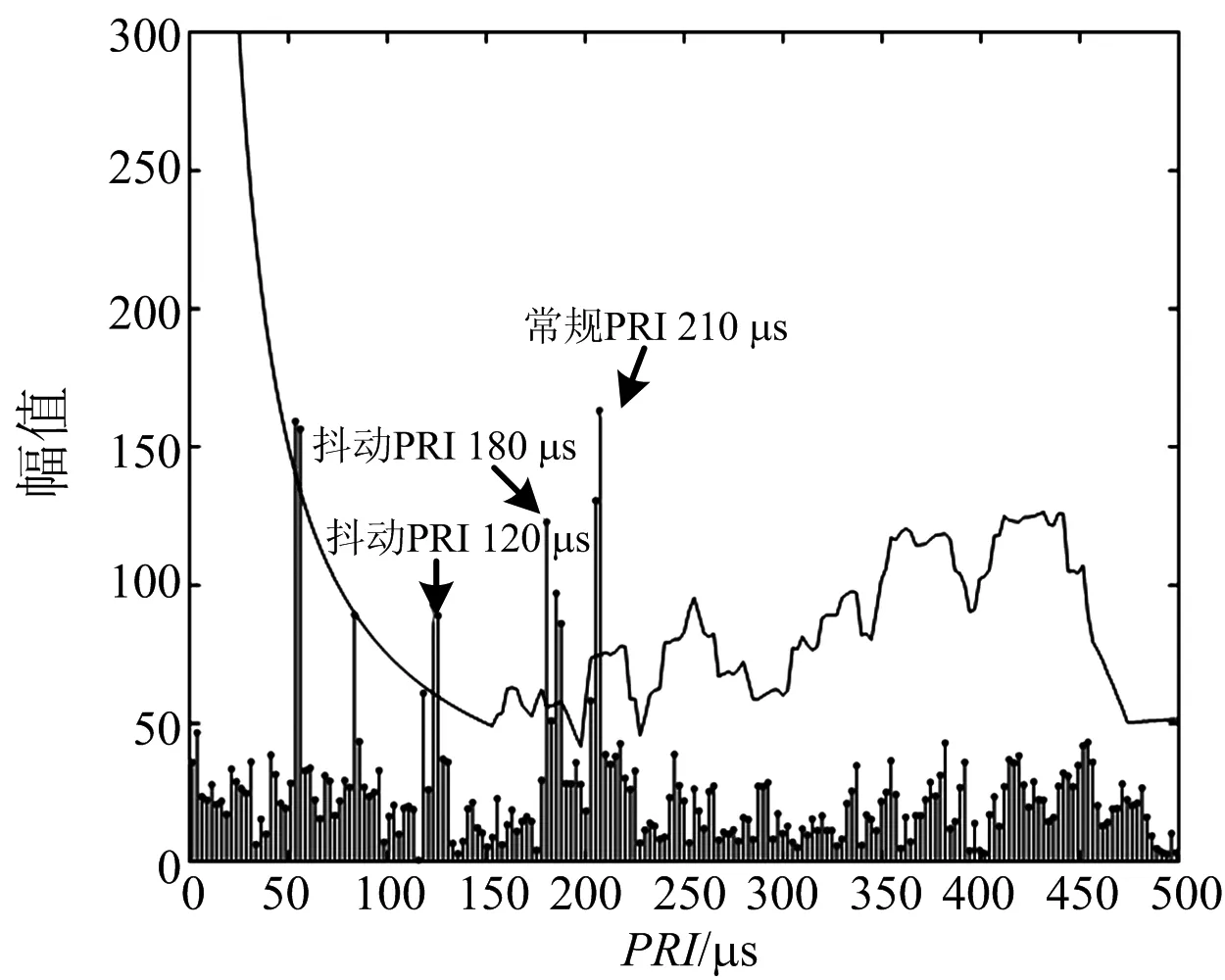
图5 PRI变换法分选结果

首先采用改进PRI变换法对5部雷达进行分选，得到分选效果图如图5所示。从图5可以看出，常规和抖动形式PRI都可以较好地被检测出来，而参差PRI检测效果差，骨架周期完全被抑制，分选困难。

接下来采用本文算法对5部雷达进行分选。

1)未改进PRI变换法检测抽取常规PRI信号,如图6所示。

图6 未改进PRI变换法检测常规PRI序列

未改进的PRI变换法有效抑制了谐波产生，准确检测出常规PRI信号210 μs，通过序列搜索对常规信号进行抽离。

2)作剩余脉冲时延自相关函数峰值图，如图7所示。

图7 时延自相关谱线图

从图中及其对应数据分析可得到4组参差PRI序列信息：

①骨架周期为107 μs，子周期个数为2；

②骨架周期为252 μs，子周期个数为3；

③骨架周期为107 μs，子周期个数为1；

④骨架周期为95 μs，子周期个数为1。

最终排除③和④，确定序列中存在两组参差PRI序列：

二参差序列，骨架周期为107 μs以及三参差序列，骨架周期为252 μs。

3)最终PRI谱线图

PRI变换法谱线图是结合由时延自相关分析得出的谱线，如图8所示。

图8 本文PRI变换法分选结果

从图8可以很清楚地检测剩余的4组雷达信号。

综上所述，可以完成对常规PRI、参差PRI以及抖动PRI的分选。

5 结束语

本文介绍了PRI变换法的基本原理，着重分析了其存在的不足，基于序列时延相关性提出了一种新的PRI变换改进算法，算法的最大改进即可以在不影响其他PRI类型分选的条件下完成对参差PRI信号的分选，仿真实验结果表明分选的效果良好。

[1] 何明浩,韩俊. 现代雷达辐射源信号分选与识别[M]. 北京: 科学出版社, 2016.

[2] NISHIGUCHI K, KOBAYASHI M. Improved Algorithm for Estimating Pulse Repetition Intervals[J]. IEEE Trans on Aerospace and Electronic Systems, 2000, 36(2):407-421.

[3] 明焱. 未知雷达信号PRI分选算法研究[D]. 西安: 西安电子科技大学, 2013.

[4] MAHDAVI A, PEZESHK A M. A Fast Enhanced Algorithm of PRI Transform[C]∥6th International Symposium on Parallel Computing in Electrical Engineering, Luton: IEEE, 2011:179-184

[5] 赵长虹,赵国庆,刘东霞. 对参差脉冲重复间隔脉冲列的重频分选[J]. 西安电子科技大学学报(自然科学版), 2003, 30(3):381-385.

[6] 柴娟芳,司锡才,马晓东. 基于PRI谱的双门限雷达信号分选算法及其硬件平台设计[J]. 数据采集与处理， 2009, 24(1):38-43.

[7] 王国立,王建华. 一种雷达信号综合分选方法研究[J]. 电子设计工程, 2013, 21(1):96-98,102.

[8] MAO Yan, HAN Jun, GUO Guohua, et al. An Improved Algorithm of PRI Transform[C]∥WRI Global Congress on Intelligent Systems, Xiamen: IEEE, 2009:145-149.

[9] 杨承志,肖卫华,吴宏超,等. 一种对多种重频调制类型雷达信号分选算法的研究[J]. 科学技术与工程, 2014, 14(34):33-37.

[10] 朱文贵,刘凯,韩嘉宾. 基于PRI变换的混叠LFM雷达信号分选[J]. 雷达科学与技术, 2016, 14(6):630-634.

ZHU Wengui, LIU Kai, HAN Jiabin. Sorting of the Aliasing LFM Radar Signals Based on PRI Transform[J]. Radar Science and Technology, 2016, 14(6):630-634.(in Chinese)