基于风速预测的改进爬山法最大功率追踪策略

姚万业， 贾昭鑫， 黄 璞

(华北电力大学 控制与计算机工程学院，河北 保定 071003)

0 引言

在高于切入风速低于额定风速段，为了最大限度地捕获风能，风电机组采用最大功率点追踪(MPPT)控制。其控制的目标在于，随着风速的变化，通过调节风轮的转速使其始终运行在最优转速即最佳叶尖速比，进而最大效率地捕获风能。

常见的最大功率追踪方法有最佳叶尖速比、功率信号反馈法、爬山搜索法等[1,2]。凭借不依靠风机特性，不需要测量风速的优势，爬山搜索法是目前无传感器最大功率追踪中的研究主流。文献[3]提出了一种追踪区间优化的最大功率点追踪策略，通过径向基神经网络优化了爬山搜索法的搜索区间。文献[4]提出了一种变步长爬山法控制策略，通过变步长保证了爬山法的追踪性能和追踪速度。文献[5]将停止机制引入爬山搜索法，通过舍弃部分低风速段的功率避免了爬山搜索法的错误搜索方向。上述改进爬山搜索法的研究工作，突破了传统方法忽略跟踪动态的局限性，取得了不错的效果。但是，由于在优化问题上很难找到彼此之间的量化关系，在风速条件多变的情况下，改进的爬山搜索法很容易出现搜索方向出错，步长过大或过小的问题。

为此，考虑到风速对功率追踪的影响，本文引入粗略风速估计[6]，提出了一种基于风速预测的改进爬山法最大功率追踪策略。首先利用LSTM神经网络模型，合理利用包括风速在内的温度、气压、空气密度等风机多传感器融合信息，对风速进行了粗略的估计，实现了较为准确的风速下一步预测，然后利用预测的下一步风速优化改进了现有的最大功率追踪爬山搜索法。实验仿真验证了引入了风速前馈的最大功率追踪策略的有效性。

1 爬山法最大功率追踪

1.1 MPPT的原理

根据贝茨理论，风力发电机的功率与风速的三次方相关，风机捕获的机械能Pm可以由空气密度ρ，桨距角β，风轮半径R和风速V表示[7,8]：

Pm(v,ω)=0.5ρπR2v3Cp(λ,β)/w

(1)

式中：CP称为风能利用系数，是关于叶尖速比λ和桨距角β的非线性函数[9]，当桨距角固定不变时，风能利用系数Cp仅与叶尖速比λ有关，叶尖速比定义为：

λ=Rω/v

(2)

联立(2)(4)可得风机的最佳功率Popt：

Popt(ω)=Koptω3

(3)

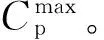
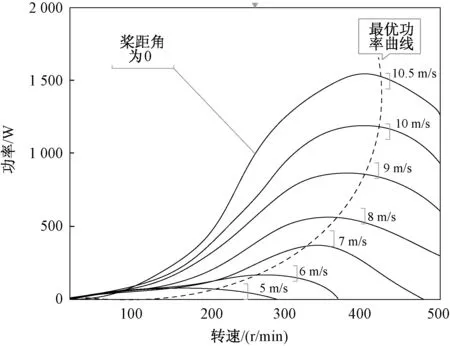
图1 最佳功率曲线的确定

1.2 爬山法

爬山法主动周期性的施加转速扰动，根据风力发电机功率—转速曲线观察扰动后系统输出功率的改变方向，从而实现最大功率追踪。目前传统爬山法主要存在2个问题：

(1)搜索区间不能自适应，搜索时间长

在爬山法中，最优功率点搜索的起始转速，就是上一时刻稳定点的转速。如果该转速与下一时刻的最优转速相差越大，则搜索时间会越长，难度会越大。

(2)搜索方向误判断和MPP点振荡

如图2所示，大步长可以加快搜索速度，但是精度无法保证，小步长可以保证精度，却不能加快收敛速度。

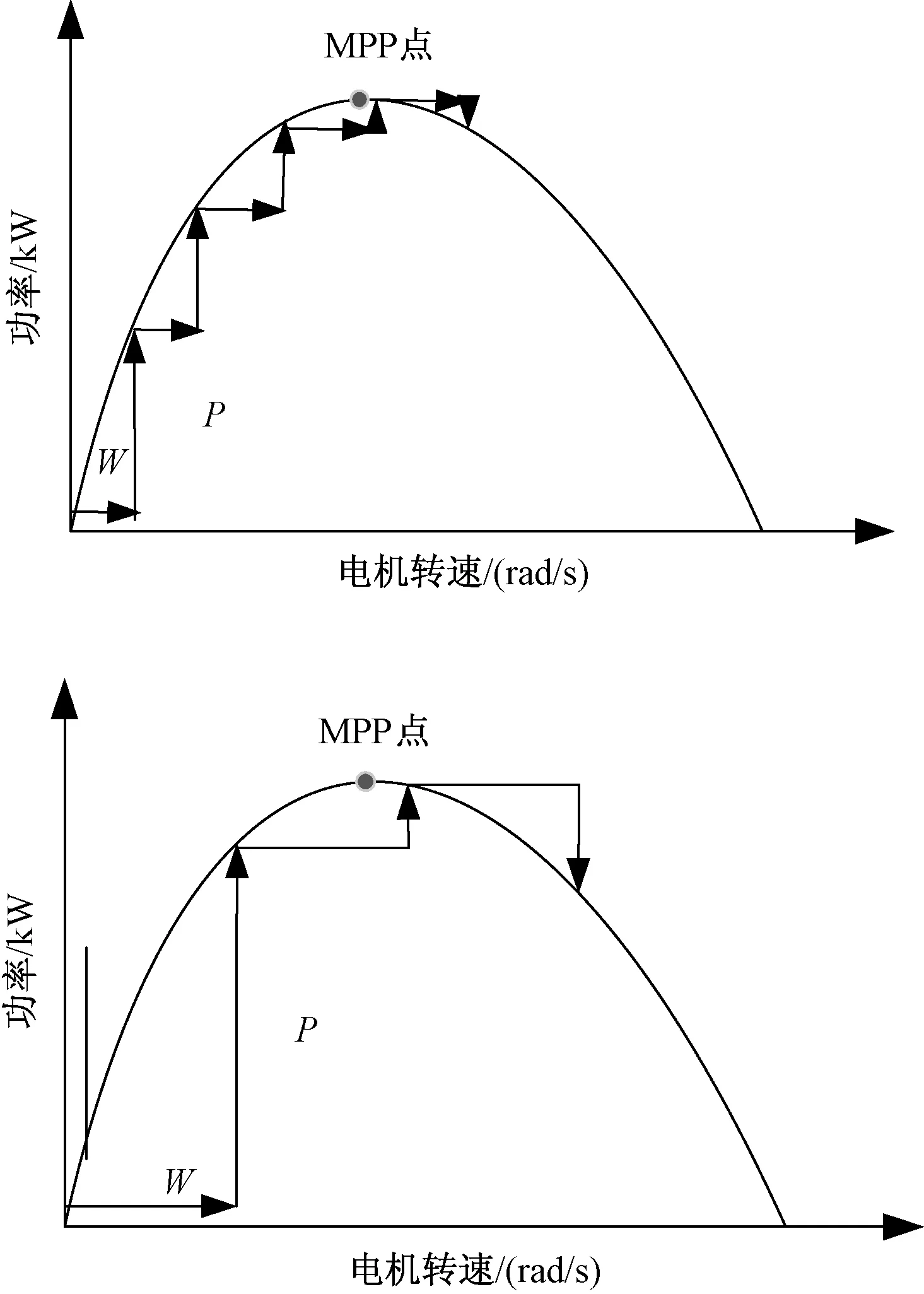
图2 不同长度Δw的扰动情况

此外传统爬山法由于步长为常量，使得风机在达到最大功率点后会一直在该点附近振动。图3反映了这种振动，频繁的振荡会影响发电机的效率和使用寿命。

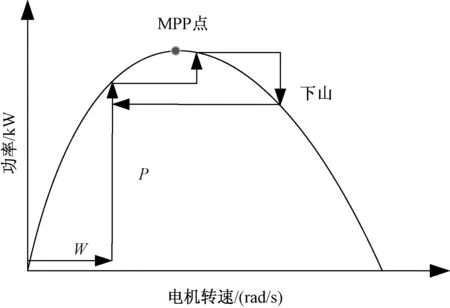
图3 MPP处的振荡

2 FRS-LSTM风速预测模型

2.1 LSTM神经网络

LSTM是一种改进的RNN，该模型可以学习长期的依赖信息，避免梯度消失的问题[10]。LSTM在RNN的隐藏层的神经节点中，增加了一种被称为记忆细胞(Memory cell)的结构用来记忆过去的信息，并增加了3种门结构(Input，Forget，Output)来控制历史信息的使用。图4为LSTM神经元结构示意图，中间部分为一个Memory Block，每个Block里面包含有多个由一组Gate控制的Memory Cell，同一个Memory Block的多个Memory Cell由同一组Gate共同控制，与LSTM相连的传送机构控制信号在BPTT时无衰减传播，通过Input Gate和Output Gate控制信息的流入与流出，通过Forget Gate决定是否重置网络，这些门的行为通过前一层的输出、上一时刻的隐藏层的输出以及记忆单元信息三者共同控制[11,12]。假设输入序列为(x1,x1,…,xr)，隐藏层层状态为(h1,h2,…,hr)，则在t时刻有：

it=sigmoid(whiht-1+wxixt)

(4)

ft=sigmoid(whfht-1+wxixt)

(5)

ct=ft⊗ct-1+it⊗tanh(whcht-1+wxcxt)

(6)

ot=sigmoid(whoht-1+whxxt+wcoct)

(7)

ht=ot⊗tanh(ct)

(8)

式中：it，ft，ot代表Input Gate，Forget Gate和Output Gate；ct代表cell单元；wh代表递归连接的权重；wx代表输入层到隐藏层的权重；sigmoid与tanh为2种激活函数。

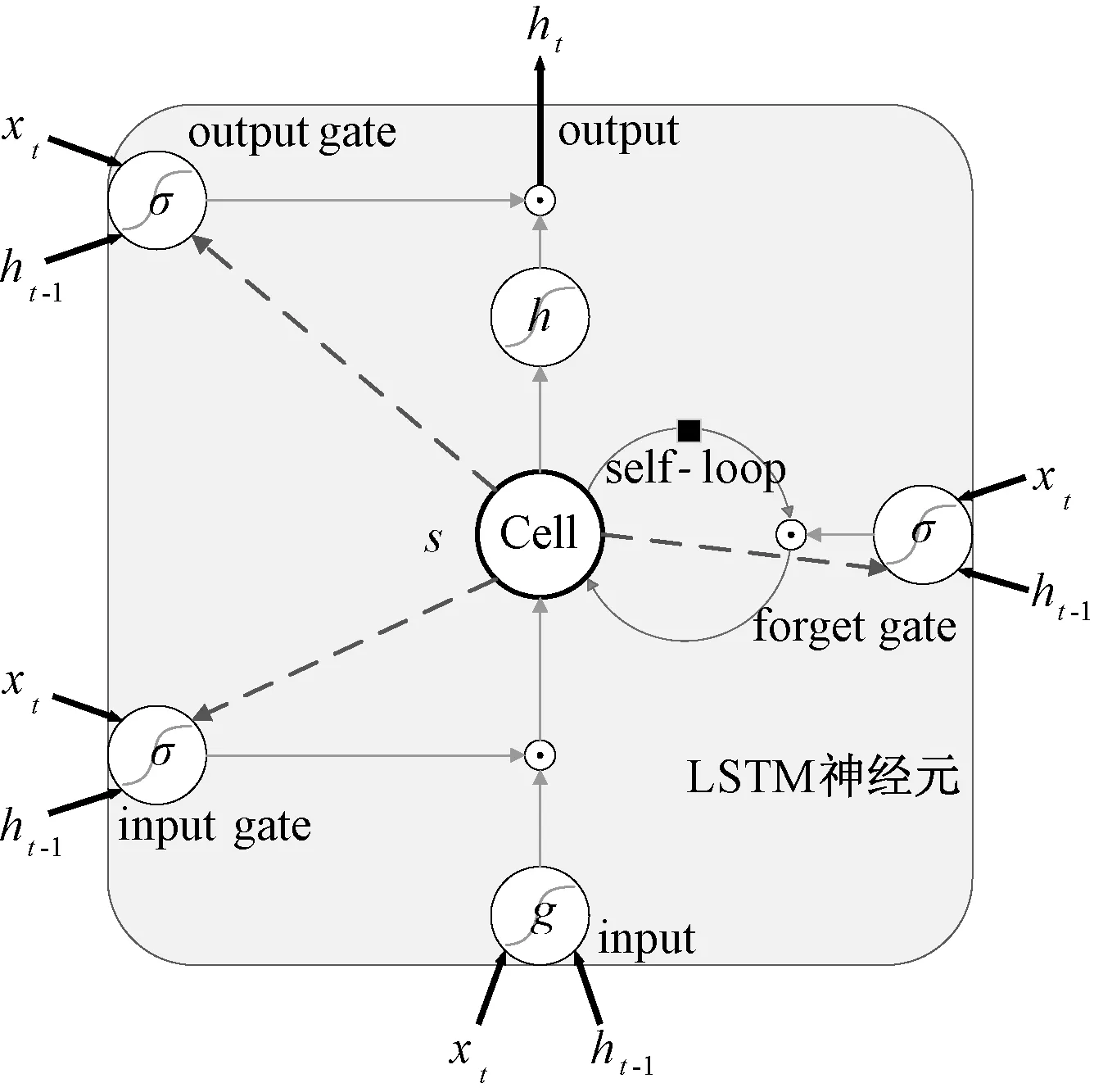
图4 LSTM神经元结构示意图

2.2 预测模型

通过传感器可采集的参数为：风速、温度、风向、空气湿度、气压。利用这些参数作为输入可设计神经网络模型完成下一时刻的风速预测。预测模型结构由模糊粗糙集因素约简(FRS)和神经网络预测(LSTM)两部分组成，利用前者对噪声的敏感性，将输入信息的空间维数简化，作为后者LSTM神经网络预测部分的输入，利用后者通过训练学习，抽取逼近隐含的输入输出非线性关系，得到风速预测的效果。

预测模型框图如图5所示。

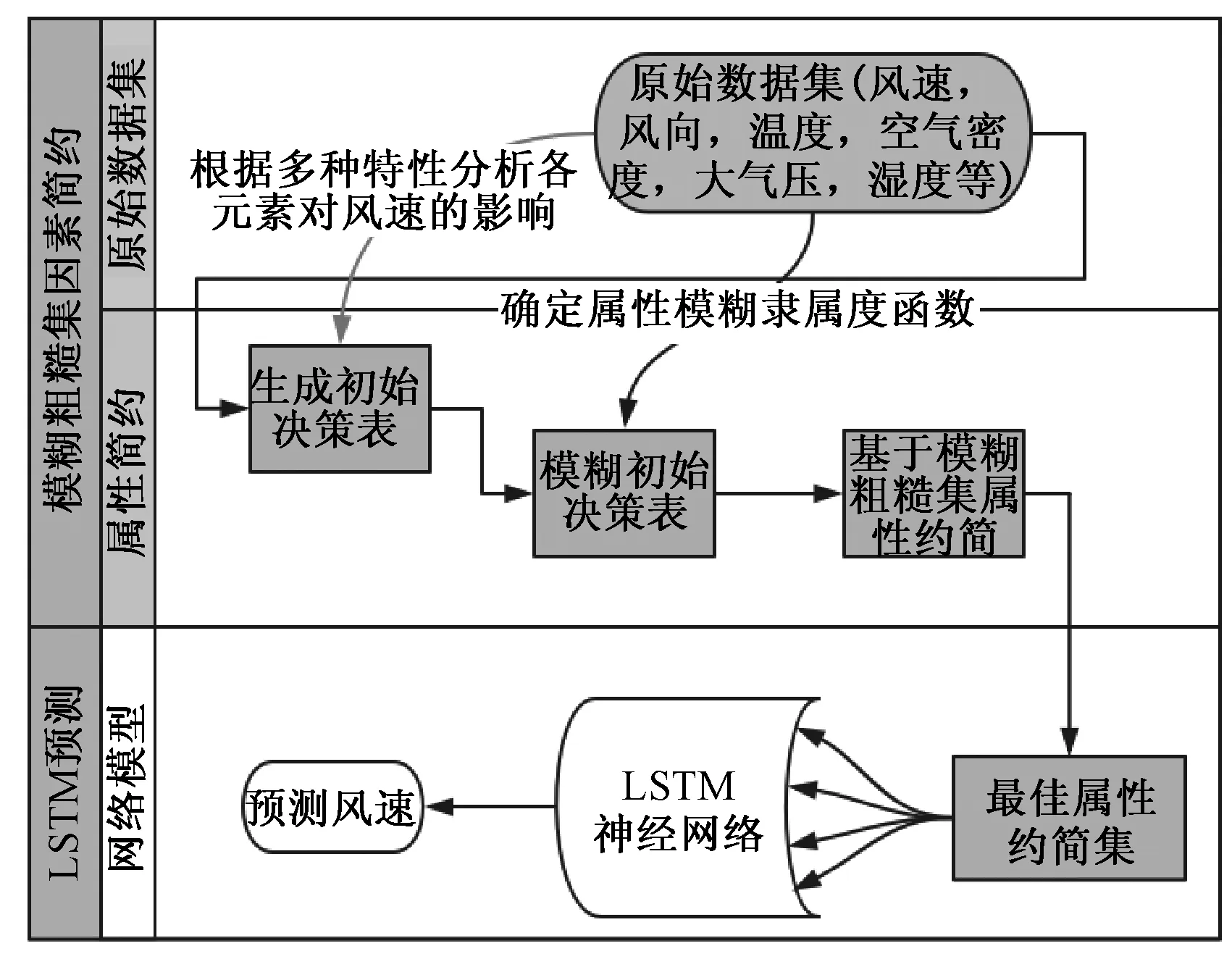
图5 预测模型框图

利用模糊粗糙集理论[13,14]进行属性约简，去除冗余信息。将预测时刻的风速v(t+1)设定为决策属性，选取35个影响因素作为条件属性，确定初始决策表。然后根据各个属性的物理特性，选取合适的模糊隶属度函数对各属性模糊，根据上文确定的各属性隶属度函数，对35个条件属性进行约简，最终确定属性集为：

R={v(t),v(t-1),v(t-2),

v(t-3),v(t-3),T(t),T(t-1)}

(9)

神经网络的输入为经过模糊粗糙集约简后的属性集R，输出为v(t+1)时刻的预测风速。

3 基于风速预测的改进爬山法

本文提出了基于风速预测的改进爬山法最大功率追踪策略，根据融合的传感器信息，依靠上文提出的LSTM神经网络预估风速，将预估的风速信息用于转矩控制算法的设计，优化追踪区间，确定搜索方向，防止MPP点处的反复振荡，改进的爬山法控制策略框图如图6所示。

图6 改进爬山法控制策略

本文从3个方面阐述改进的爬山法：

(1)优化追踪区间

如图7所示，当风机运行在K时刻，风速为v(k)，风电机组能够稳定运行在该风速下，此时的转速为最优转速wopt(k)，即点A，在爬山搜索法中，点A就是下一时刻搜索的起始位置，该时刻的转速wopt(k)就是下一时刻(k+1)时刻的搜索起始转速。

图7 追踪区间优化

假设(k+1)时刻，风速变为v(k+1),风电机组将在控制策略的作用下重新搜素新风速下对应的最佳功率点。搜索区域为A-C段。此时，利用k时刻预测出(k+1)时刻的风速为vp(k+1)，根据公式(12)推出(k+1)时刻的风电机组转速wpre(k+1)：

wpre(k+1)=λopt·vP(k+1)·N/R

(10)

将转速wpre(k+1)替代wopt(k)作为(k+1)时刻最大风能追踪的初始转速,即将初始搜索点从A点移动到B点，搜索区域变为B-C段。(k+1)时刻，对应风速v(k+1)的最优功率点转速为wopt(k+1)。(k+1)时刻的MPPT中，如采用传统无风速预测爬山法，起始转速与最优转速的差值为：

Δw=wopt(k+1)-wopt(k)=

λopt·[v(k+1)-v(k)]·N/R

(11)

改进爬山法后，新的起始转速与最优转速的差值为：

Δw′=wopt(k+1)-wini(k+1)=

λopt·[v(k+1)-vp(k+1)]·N/R

(12)

所以使用了提前的风速预测后，爬山法搜索的区间由Δw缩减为Δw′，搜索效率大大提高。实验发现，由于缩小了追踪区间，扰动值的选取变得比较重要，少许的变化可能就会产生振荡，所以在收缩区间的优化上引入收缩系数α，根据v(t)与v(t+1)的变化幅度改变系数α，当风速变化过快时，大的α保证收缩区间收缩的不至于过小，当风速变化不大时，小的收缩系数α保证收缩的不至于过大。

(2)确定搜索方向

当风速稳定时，根据爬山法的原理，通常的搜索方向判断为由式(13)决定：

(13)

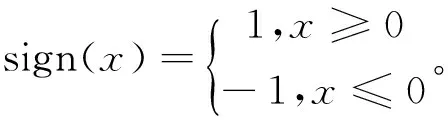
当风速出现波动的时候，用预测风速的变化代替功率的变化值，完成搜索方向的确定，由式(14)决定：

(14)

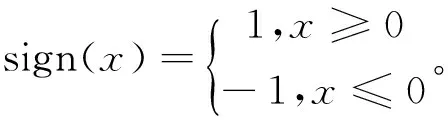
(3)避免MPP点的波动

当(k+1)时刻最大风能追踪的起始搜索区域确定为wini(k+1)后，采用变转速扰动MPPT控制来找到最优功率点。在2个相邻的离散时间点(n-1)和n，对机组的输出功率和转速进行采样，计算风电机组功率的斜率dPT/dwT：

(15)

风电机组转速扰动可取为：

Δw=KMPPT(dPT/dwT)

(16)

当|ΔPT|=|PT(n)-PT(n-1)|

4 算例分析

采用GH-Bladed软件进行仿真验证，由于软件仿真的局限性，对属性约简集进行了微调，输入变量的选取采用了适当的删减。仿真采用1.5 MW风机模型，风机参数如表1所示。

表1 风力发电机组整机参数

本文主要仿真的部分在额定风速以下，即桨距角为0°状态。分别采用平均风速6 m/s，7 m/s，8 m/s，9 m/s的4种3D湍流风进行仿真验证。仿真采用了统一变桨方式，在仿真过程监控4个数据，分别为：桨角，测量的转速，设定的转矩，轮毂处测量风速，输出功率。

仿真中200～300 s发生了风速突变，选取该100 s内进行分析，风速预测效果如图8所示，控制策略仿真结果如图9所示。

图8 预测结果

图9 仿真结果

由仿真结果可得，新提出的基于风速预测的改进爬山法：

(1)有效避免了风速变化情况下的错误搜索方向。如图圆圈标注的部分可以明显看出，当风速发生变化的时候，传统爬山搜索法出现了错误的搜索方向，本应该减小转速的时候，却朝着转速增大的方向搜索，改进的爬山法则有效避免了该方向的错误。

(2)明显减少了风机在MPP点处的振荡。长方形标注的部分可以看出，优化的爬山搜索法转速控制更加平滑，避免了频繁的转速切换。

(3)有效提高了风能捕获效率。由公式(17)计算的风能捕获效率，改进的爬山搜索法为97.1%，传统的爬山搜索法为95.3%。

(17)

式中：ΔPmax为所示功率；Pcap为实际捕获的风能；Pmax为捕获风能理论值。

5 结论

相对于传统的最大功率追踪策略，本文提出了一种基于风速预测的改进爬山法控制策略，融合风机运行过程中的各种传感器信息，利用深度学习神经网络，实现了下一时刻风速的预测，通过预测的风速有效地收缩了风机转速的追踪区间，确定了正确的搜索方向，避免了MPP点处频繁的振荡，实验仿真表明了该方法的有效性。

[1]李鑫,曾令全,侯斌,等. 风力发电仿真系统中模拟风轮机的理论研究[J]. 华北电力大学学报(自然科学版),2010,37(6):17-22.

[2]李梓萌,李洪举,冯洁. 基于模糊控制结合扰动观察法的风力发电系统MPPT控制策略[J]. 电力科学与工程,2016,32(11):18-22.

[3]殷明慧，张小莲，邹云，等. 追踪区间优化的风力机最大功率点追踪控制[J].电网技术，2014，38(8)：2180-2185.

[4]钟沁宏，阮毅，赵梅花，等.变步长爬山法在双馈风力发电系统最大风能跟踪控制中的应用[J]. 电力系统保护与控制，2013，41(9)：67-73.

[5]张小莲, 李群, 殷明慧,等. 一种引入停止机制的改进爬山算法[J]. 中国电机工程学报, 2012, 32(14):128-134.

[6]高阳,钟宏宇,陈鑫宇,等.基于神经网络和小波分析的超短期风速预测[J].可再生能源,2016,34(5):705-711.

[7]祝晓燕,张金会,付士鹏,等. 基于集合经验模态分解和支持向量机的短期风速预测模型[J]. 华北电力大学学报(自然科学版),2013,40(5):60-64.

[8]石亚欣. 基于时间序列的WD-LS-SVM的风速周期预测模型研究[J]. 电力科学与工程,2014,30(2):41-45.

[9]李东福,董雷,礼晓飞,等. 基于多尺度小波分解和时间序列法的风电场风速预测[J]. 华北电力大学学报(自然科学版),2012,39(2):43-48.

[10]ZHAO Z，CHEN W，WU X，et al.LSTM network: a deep learning approach for short term traffic forecast[J].Let Intelligent Transport Systems，2017，11(2)：68-75.

[11]杨训政，柯余洋，梁肖，等.基于LSTM的发电机组污染物排放预测研究[J].电气自动化，2016，38(5)：22-25.

[12]LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553):436.

[13]刘兴杰，岑添云，郑文书，等.基于模糊粗糙集与改进聚类的神经网络风速预测[J].中国电机工程学报，2014，34(19)：3162-3169.

[14]尹东阳，盛义发，蒋明洁，等.基于粗糙集理论-主成分分析的Elman神经网络短期风速预测[J].电力系统保护与控制，2014，42(11)：46-51.