光伏电池工程仿真模型在污垢评估中的应用

王 冰， 石 敏， 童 正， 韩立刚， 李晓江

(1.北京京能新能源有限公司内蒙古分公司， 内蒙古 呼和浩特 010070；2.山西漳山发电有限责任公司,山西 长治 046021)

0 引言

近年来，随着光伏电池原材料、逆变器等主要器件成本的降低及政策扶持力度的加大，光伏发电越来越受到重视，进而得到了广泛、迅速推广。目前，光伏发电已经成为可再生能源领域中继风力发电之后发展最快、最大的产业[1]，光伏电站的运维也随之显得尤为重要。

在实际运行过程中，沉积在组件表面的灰尘积垢会导致组件的转换效率下降，因此有必要针对灰尘、积垢对光伏性能的影响进行研究。查阅资料，国内外一些专家也对此进行了相关分析，其中文献[2]得出积灰密度与光伏组件上层玻璃相对透光率、光伏组件工作温度以及发电功率的耦合关系；文献[3]通过搭建试验平台验证了灰尘积累浓度越高，组件性能下降越大；文献[4]研究表明，组件电压和功率的降低主要取决于污染物类型和沉积水平，灰尘污染物是光伏组件电压中影响最大的粉尘颗粒，当使用灰尘污染物时，组件电压约下降25%。

根据调研，目前我国大部分光伏电站仍仅根据人工观察光伏电池的积灰程度来确定是否开展清洁工作，过分依赖运维人员经验，缺乏科学性，而且人工清洁作业工作量大、成本高。本文参考专家的研究成果，对光伏电池进行了深入分析，建立了数学模型，搭建了MATLAB仿真平台。在此基础上提出了一种灰尘、积垢对光伏电池发电量影响的评估方法，结合光伏电池板的开路电压与短路电流测量，科学评估灰尘、积垢对光伏电池发电量的影响，据此合理地制定清洁作业规划，有效节约维护成本。

1 光伏电池模型与修正

1.1 光伏电池等效模型

光伏电池是利用半导体材料的光生伏特效应将太阳能转化为电能，其工作时实质就是一种电源。光伏电池可以等效为电流源电路，若负载为纯电阻，其电路如图1所示，可以用来分析光伏电池的外特性。

图1 光伏电池等效电路

由电路图可推导出其IV方程为[5-9]：

I=Iph-ID-Ish

(1)

(2)

(3)

式中：I为太阳电池的输出电流；V为太阳电池的输出电压；Iph为光伏电池的光生电流，其不随电池的工作状态而改变，大小约为光伏电池的短路电流；ID为流经P-N结二极管的暗电流；I0为电池的二极管反向饱和电流；Rs为串联等效电阻，由半导体材料的本体电阻、半导体材料与电极间的电阻及电极本身的电阻组成，其值比较小，一般在10-3到几欧姆之间；Rsh为并联等效电阻，由电池表面污染、及在制作中产生的裂痕形成的漏电流等原因产生的，其值一般比较大，在1 000 Ω以上。q为单位电荷，其值为1.6×10-19C；A为二极管因子，其值常在1～2变化；K为波耳兹曼常数，其值为1.38×10-23J/K；T为绝对温度。

由(1)(2)(3)式得：

(4)

1.2 模型工程修正

工程实际应用中，厂商一般提供Voc、Ioc、Vm、Im4个参数，上述方程显然并不合适。需对方程(4)进行修正，一般遵循以下3个原则[10-12]：

(1)通常情况下，Rsh比较大，Rs比较小，(V+IRs)/Rsh远远小于光伏电池的光生电流Iph，故该项可以忽略。

(2)由于短路时流经二极管的暗电流ID非常小，则光生电流约等于短路电流，Iph≈ISC。

(3)串联等效电阻Rs比较小，IRs远远小于V，故IRs也可以忽略。

根据上述原则，令C1=I0/Isc，C2=q/AKT

则(4)可以简化为[4-7]

I=Isc{1-C1[eC2V-1]}

(5)

在最大功率点：I=Im，V=Vm；在开路情况下：I=0，V=Voc可以得出：

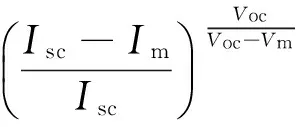
(6)

(7)

将(6)(7)代入(5)即可得到工程应用的标况条件(S=1 000 W/m2，T=25 ℃)下的IV简化方程：

(8)

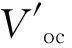
(9)

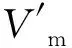
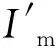
(10)

式中：Sref为标况下的太阳辐射强度，其值为1 000 W/m2。根据工程实际应用的经验数据可知，a=0.002 5 ℃，b=0.000 5，c=0.002 88 ℃。由(9)(10)可以推导出，

(11)

式中：Voc、Ioc、Vm、Im为标准测试条件下(STC)的测量值；Voc′、Ioc′、Vm′、Im′为非标准测试条件下(NOCT)的测量值。

2 模型仿真与验证

以内蒙某光伏电站型号为250P-29的光伏电池组件为例进行仿真，表1为电池组件标准测试条件下的标称参数表。

表1 电池组件参数表

综合以上分析建立的光伏电池仿真模型，如图 2 所示。结合电站实际运行状态，设置仿真参数如下：标准状态下光强S=1 000 W/m2，温度T=25 ℃，开路电压Voc=38.4 V，短路电流Isc=8.79 A，最大功率点电压Vm=30.4 V，电流Im=8.24 A。不同的光照强度和环境温度时，通过仿真模型可以计算出光伏电池的I-V和P-V曲线，仿真曲线如图3所示。表明：1、辐照度与光伏电池的峰值功率有高度正相关性，具有正比关系。2、光伏电池的开路电压随温度的升高而下降，短路电流随温度的升高而升高，峰值功率随温度的升高而降低。从大部分厂家提供的数据来看，峰值功率温度系数为-0.45%℃，按照峰值功率为250 Wp的组件来计算，在基准温度25 ℃的基础上，每上升1 ℃，组件的功率基本下降1 Wp。

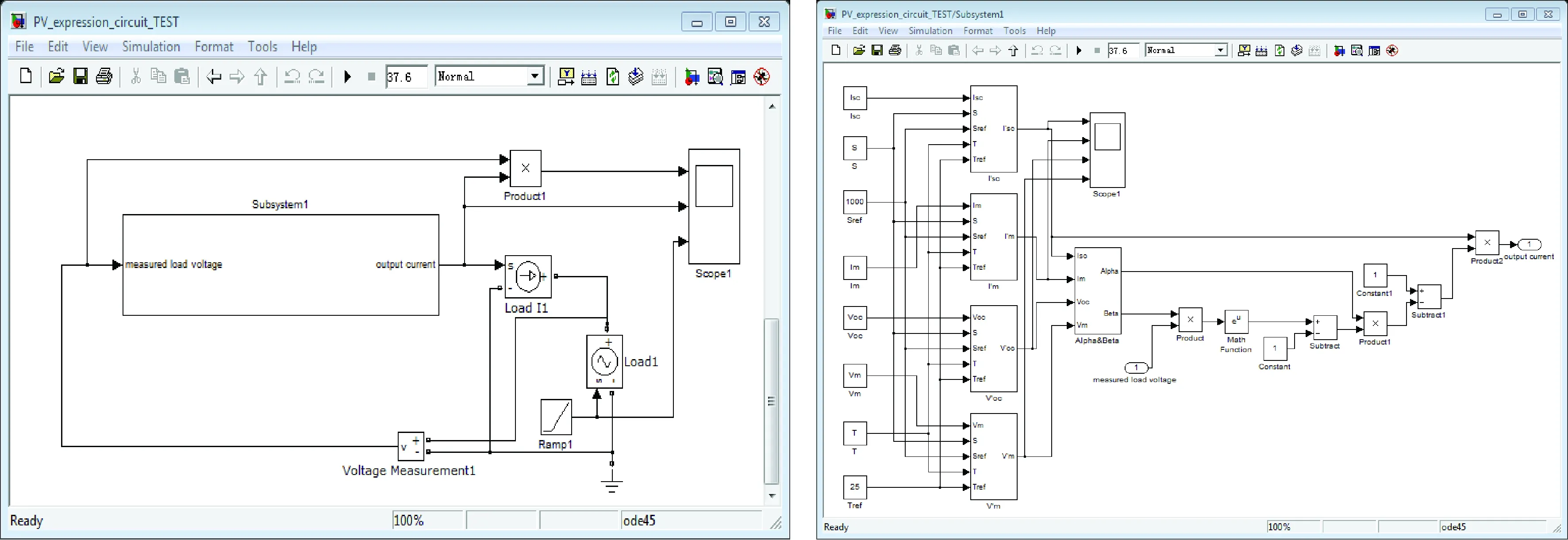
图2 光伏电池MATLAB仿真模型的搭建

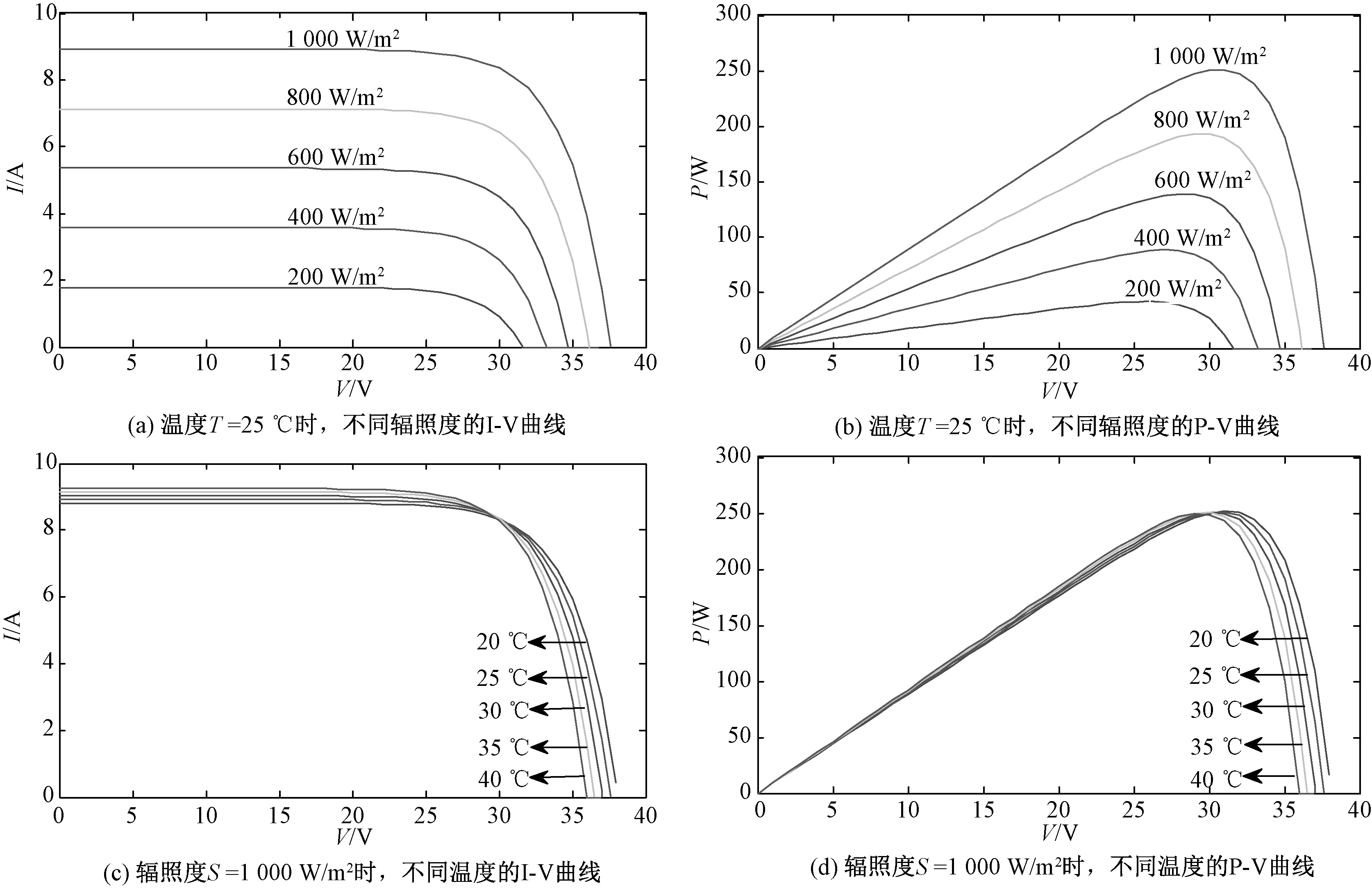
图3 光伏电池输出特性仿真结果

图3中的仿真数据与光伏电池板厂家提供IV测试曲线相比较，如表2所示，Pmp1为厂家提供的数据，Pmp2为仿真数据，结果表明仿真数据与实际数据误差都在5%以内，验证了根据光伏电池工程模型搭建的仿真模型的准确性。

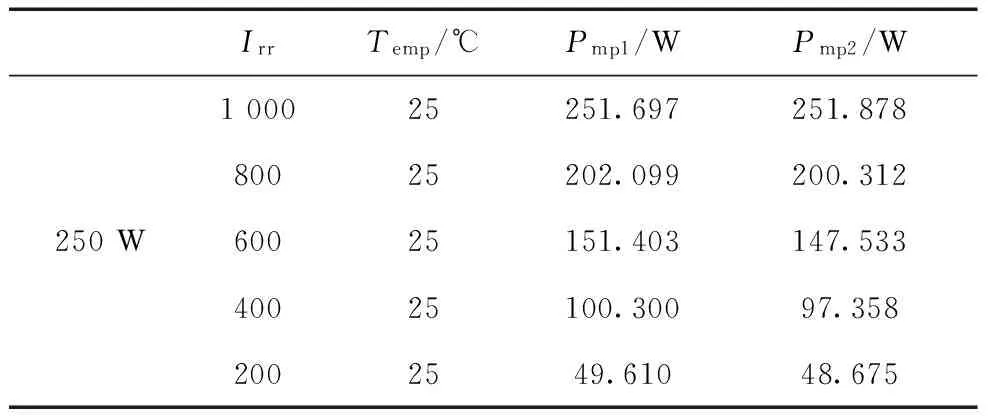
表2 实际数据与仿真数据对比

3 基于光伏电池工程模型的灰尘评估

3.1 评估装置与原理

本文提出的灰尘、积垢对光伏电池发电量影响装置如图4所示，主要包括：(1)光伏电池板1；(2)光伏电池板2；(3)光伏电池板开路电压与短路电流检测装置；(4)灰尘积垢对光伏电池发电量影响评估模块。其中，通过配有自动清洁系统或者采用人工经常清洁的方法，保证光伏电池板1处于清洁状态，光伏电池板2则没有清洁系统，其表面灰尘、积垢自然累加。

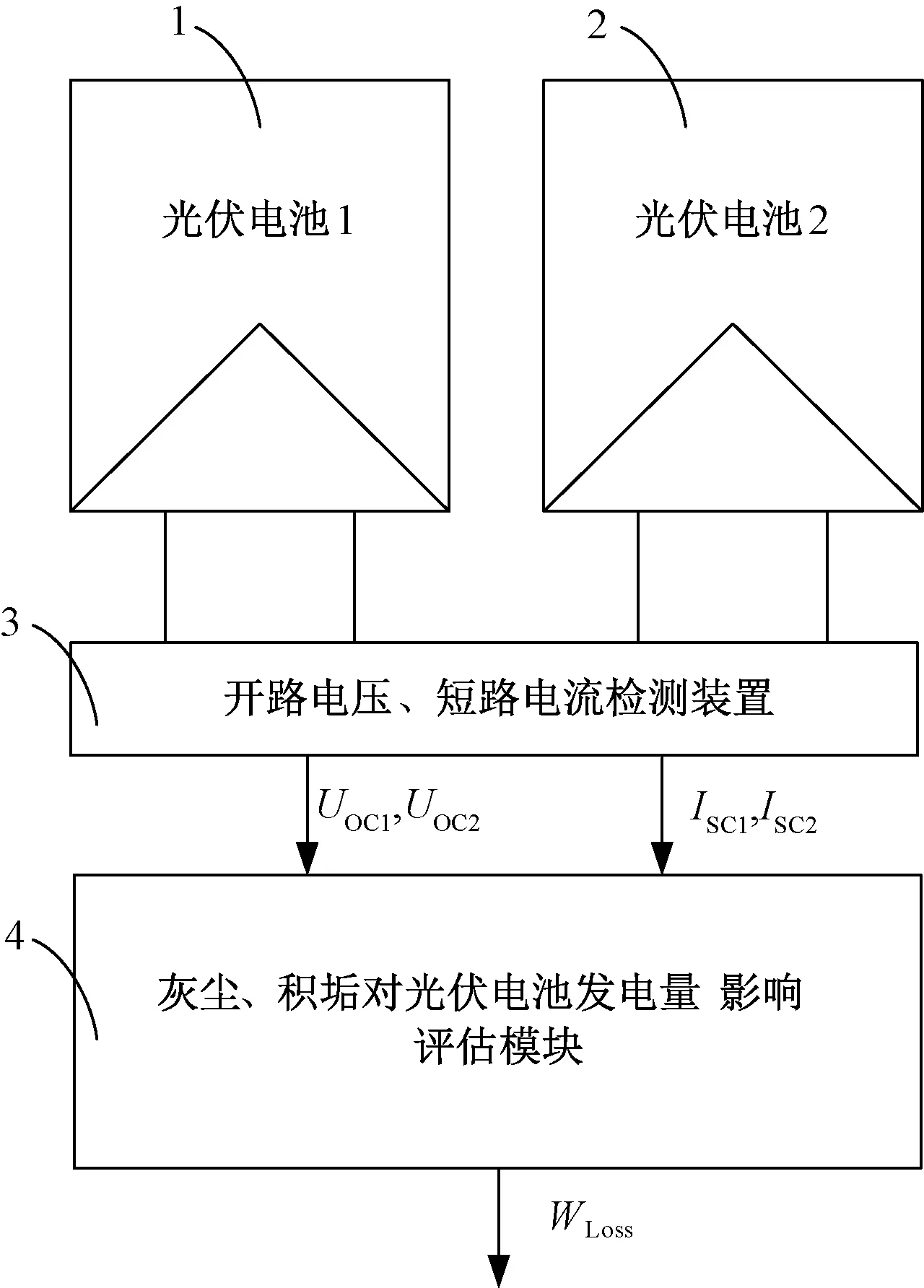
图4 评估原理

目前，灰尘对光伏组件的影响很大，在工程实际应用中没有一种合理有效的预测光伏组件清洗周期的方法。由于现在大部分的光伏逆变器采用的控制策略为MPPT技术，其理论基础为太阳电池板的输出功率P(t)=VmIm，因此只要得到实际的Vm和Im即可算出光伏板的发电量。关键问题是Vm和Im随着光照和温度等环境温度的不断变化，直接测量不易实现。光伏电池板输出参数随光照和温度等环境因素而变化，由式(11)推理可知，其标况下的开路电压、短路电流、额定电压、额定电流与非标况下成正比。根据光伏组件的数学模型搭建仿真模型，通过测量实时(非标况下)的开路电压和短路电流来推算实际发出的功率。

3.2 评估步骤

对于灰尘、积垢对光伏电池发电量影响的评估步骤如下：

(1)按设定时间间隔ΔT采样光伏电池板1和光伏电池板2的开路电压UOC1、UOC2与短路电流ISC1(k)、ISC2(k)。

(2)根据实时采样参数，结合光伏电池工程用数学模型，就按当前环境条件(光照强度、温度等)下光伏电池板1和光伏电池板2的I-V曲线，计算当前情况下光伏电池板1和光伏电池板2的最大输出功率Pm1(k)、Pm2(k)。

(3)计算当前时刻光伏电池板1和光伏电池板2的最大输出功率差Pm1(k)-Pm2(k)。

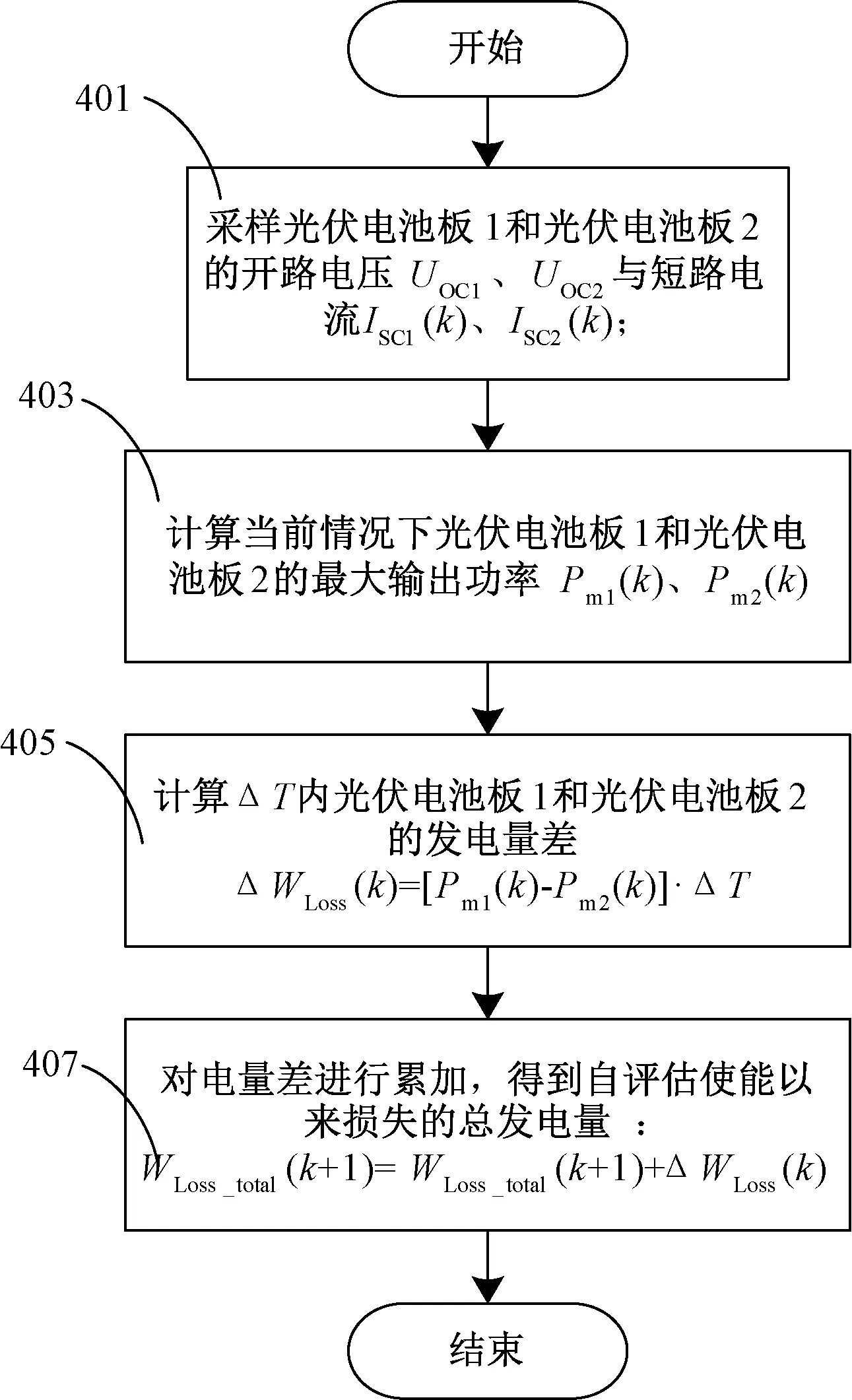
图5 灰尘对光伏电池发电量影响的评估步骤

(4)计算ΔT内光伏电池板1和光伏电池板2的发电量差ΔWLoss(k)=[Pm1(k)-Pm2(k)]·ΔT。

(5)对电量差进行累加，得失的总发电量WLoss_total(k+1)=WLoss_total(k+1)+ΔWLoss(k)。

上述评估装置结合测光伏电池板的开路电压、短路电流就能对灰尘、积垢对光伏电池发电量影响进行科学评估，在光伏电站已经得到了实际应用，基于仿真模型的评估方法在现场得到推广应用。对光伏组件的清洁周期进行合理规划，有效的节约了系统维护成本。

3.3 实验验证

采用评估装置对某光伏电站的发电量进行评估，运行30天，光伏电池板1与光伏电池板2的理论发电量相差2%，对光伏组串进行清洁，清洁后发电量得到明显提升，如图6所示，试验期间平均发电效率提升2%以上，清洁成本投入小于200元/MWp。以容量为20 MWp的光伏电站为例，每天按5 h满发运行计算，30天提升电量6万kWp，清洁成本投入为4 000元，效益比较明显。根据当地电价及清洁成本，可以适当调整清洁周期。试验表明，该评估装置对对光伏组件的清洁具有指导作用，依据当地的气候情况，按周期进行合理规划清洁周期，可有效提高系统发电量。

图6 清洁效果对比曲线

4 结论

(1)根据光伏电池的模拟电路图推出的仿真模型不适合工程应用，需按照实际工程数据进行修正以适应实际需要。考虑到IV特性曲线与太阳辐射和环境温度关系密切，经过环境参数修正后的数学模型及仿真模型可以模拟在现场实际工程应用中不同条件下的电池特性。以型号为250P-29的光伏组件为例，将实际功率输出与仿真数据输出相比较，其误差在5%以下，从而验证了仿真模型的准确性。

(2)基于工程仿真模型的灰尘评估方法，通过测量两块光伏电池板的开路电压、短路电流对灰尘对光伏电池发电量影响进行科学评估，据此制定合理的清洁作业规划，节约维护成本。

[1]戚军，张晓峰，张有兵，等.考虑阴影影响的光伏阵列仿真算法研究[J].中国电机工程学报，2012，32(32)：131-138.

[2]官燕玲，张豪，闫旭洲，等.灰尘覆盖对光伏组件性能影响的原位实验研究[J].太阳能学报，2016，37(8)：1944-1950.

[3]张风，白建波，郝玉哲，等.光伏组件表面积灰对其发电性能的影响[J].电网与清洁能源，2012，28(10)：82-86.

[4]Effect of dust deposition on the performance of multi-crystalline photovoltaic modules based on experimental measurements[J].International Journal of Renewable Energy Research，2016，3(4):850-853.

[5]赵争鸣.太阳能光伏发电及其应用[M].北京：科学出版社，2005.

[6]金新民.主动配电网中的电力电子技术[M].北京：北京交通大学出版社，2015.

[7]茆美琴，余世杰，苏建徽.带有MPPT功能的光伏阵列Matlab通用仿真模型[J].系统仿真学报，2005，17(5)：1248-1251.

[8]DIRNBERGER D. On the uncertainty of energetic impact on the yield of different PV technologies due to varying spectral irradiance[J].Solar Energy, 2015, 111(111):82-96.

[9]北京地区多种光伏组件发电性能对比实验研究[J].可再生能源,2016，34(8)：1117-1123.

[10]王以笑，崔丽艳，雷振峰,等.分布式光伏电站区域智能调控系统的研究[J].电力系统保护与控制，2016(4):118-122.

[11]张莹，李明，张子扬,等.失配条件下集中式并网光伏发电系统性能研究[J].太阳能学报,2016，37(10)：2512-2518.

[12]高立刚.大型并网光伏电站集中式与组串式逆变器整体解决方案分析[J].太阳能，2016(2)：14-21.