基于分数阶傅里叶变换的ISAR横向定标*

云 涛 俞 翔 王 军 王 坤 衣尚军 周洪喜

(1. 中国人民解放军63778部队，佳木斯, 154002； 2. 南京航空航天大学电子信息工程学院, 南京, 210016)

引 言

目前ISAR目标转角估计的方法主要有：轨迹拟合法[2]、多天线干涉法[3]、层析成像法[4]、互相关法[5]、回波参数法[6]及特征线斜率法[7]。轨迹拟合法利用雷达窄带跟踪数据，对目标轨迹进行滤波、拟合等处理，从而计算目标相对于雷达的转角；但由于窄带信号跟踪数据精度较低，同时对于目标自身转动的估计无能为力，对复杂运动目标的估计误差更大。多天线干涉法利用多天线相干处理技术对两幅天线接收到的回波信号进行相位干涉，估计转动矢量大小，进而完成横向定标，但系统太复杂，成本较高。层析成像法利用卷积反投影方法获得在各种角度参数情况下的目标图像，然后根据峰值最大准则估计最优转角，但每次层析成像的计算量比较大。互相关法通过搜索使两幅ISAR图像的相关性最大的等效转动角速度来完成横向定标。该方法假设目标的等效旋转中心和几何中心一致，但在实际成像中这种假设并不总是正确。回波信号参数法是对一类方法的统称，通常在慢时间域对回波信号进行建模分析，认为回波信号是线性调频信号，或者具有二次相位项，并且其中的参数同转动角速度存在确定关系，通过数学工具估计这些参数，从而计算旋转角速度，进而完成横向定标。该方法定标效果受制于运动补偿效果和参数估计的精度，尤其对于等效转速度较低的目标，慢时间域线性调频信号调频率很低，较难估计。特征线斜率法利用目标俯视图的两条特征线即可完成定标；但该方法需要对图像进行二值化处理，然后进行Radon变换。在进行二值化处理时，不同阈值对于后期估计精度有很大影响，且阈值难以通过计算得到；同时在进行Radon变换时可能会产生模糊峰值。

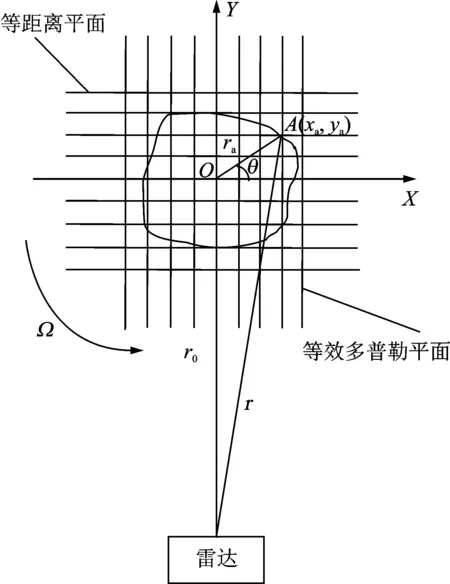
图1 转台成像示意图 Fig.1 Turntable imaging

分数阶傅里叶变换作为傅里叶变换的广义形式，是一种统一的时频变换，同时反映了信号在频域和时域的信息，由于其独有的特性，近年来在众多领域得到了广泛应用[8-11]。 本文基于回波信号参数法，给出了一种基于分数阶傅里叶变换(Fractional Fourier transform, FrFT)的ISAR横向定标方法，此方法假设目标在相干积累时间内运动平稳。在此前提下，本文首先对ISAR回波信号进行分析建模，确定回波信号在慢时间域为线性调频信号，然后利用FrFT估计出信号的调频率，求得相干积累时间内目标等效转动角速度，从而实现横向定标。

1 回波信号分析

相干积累时间运动平稳的目标，经过运动补偿以后，转化为转台运动。转台成像示意图如图1所示。图1描述的是一个匀速转动的三维目标投影到二维成像平面上。r0为目标的等效旋转中心到雷达的距离，Ω为目标绕自身o点的等效旋转角速度。在起始时刻(即t=0)，目标上的任意一点A(xa,ya,za)到雷达的距离为

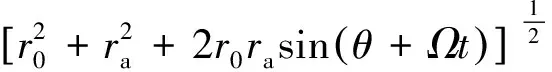
(1)

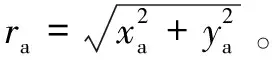
r≈r0+xasinΩt+yacosΩt

(2)

目标上该点的多普勒频率可以表示为

(3)

式中:λ为雷达波长。由于相干积累时间很短，此时目标的旋转角度Δθ=Ωt很小，则式(3)可以近似成

(4)

由式(4)可知，各散射点回波信号在慢时间上表现为线性调频信号，目标的等效旋转角速度与该信号的调频率存在确定关系，其调频率K和多普勒初始频率f0分别为

(5)

(6)

式(6)中，由于距离向定标很容易完成，则ya可知，λ已知，所以根据回波信号的调频率K，就能计算出旋转角速度Ω。可见旋转角速度的估计问题转换为估计信号的调频率K。若雷达发射脉冲信号的脉冲周期用T表示，则发射时刻tm=mT(m=0,1,2,…)称为慢时间。本文的研究基于慢时间域，后文中没有特别强调时间的情况下的时间均指慢时间。

2 分数阶傅里叶变换原理

通常，函数f(u)的p阶分数阶傅里叶变换可以表示为fp(u)[12]。分数阶傅里叶变换的基本表达式为

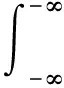
(7)

式中Kp(u,t)为分数阶Fourier变换的核函数，则

(8)

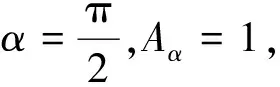
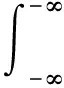
(9)

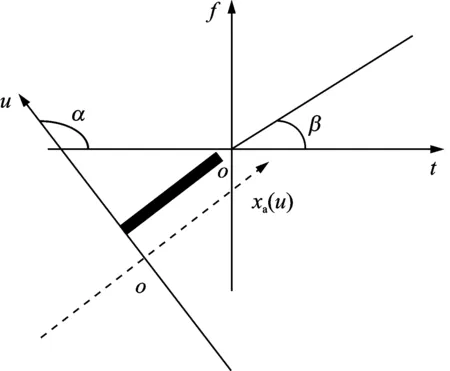
图2 LFM信号时频分布及FrFT示意图 Fig.2 LFM signal time-frequency distri-bution and FrFT schematic diagram

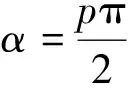
3 有效转动角速度的估计

线性调频(Linear frequency modulation，LFM)信号在不同的分数阶傅里叶域上呈现不同的能量聚集性[13,14]。LFM信号的分数阶傅里叶变换相当于将信号的时频分布投影在不同旋转角度的频率轴上，在特定的旋转角度，LFM信号能量会得到高度集中。所以检测LFM信号的基本方法如下：在变量旋转角α的某个取值区间内，利用FrFT对信号进行处理，形成能量在参数(α,u)平面上的二维分布，并按阈值进行搜索即可实现。

单个LFM信号的时频分布及其FrFT如图2所示，LFM信号与时间轴的夹角为β，斜率即为其调频率，旋转轴与时间轴的夹角为α，当α=β时即为该信号的傅里叶变换。当α与β正交时，该LFM信号在分数阶傅里叶域上的投影聚集在一点上，此时能量最强[15]，该LFM信号的调频率为

K=-cot(α0)

(10)

在ISAR图像中，同一个距离单元内往往包含多个散射点。各散射点引入的多普勒频率的时频分布如图3(a)所示。式(5)决定了这些信号在频率f轴上的截距，式(6)决定了这些信号的调频率，即图2中的斜率。

由于调频率由散射点的纵向距离单元ya和目标相对雷达的转速Ω决定，所以，同一纵向距离单元的各散射点的回波信号的调频率相同。本文只关心信号的调频率，所以同一距离单元的多个LFM信号的FrFT变换对应的幅度，会在同一个确定的变换参数下达到最大值，如图3(b)所示。

图3 同距离单元不同横向距离散射点回波FrFT处理

Fig.3 Fractional Fourier transform of scattered echo with different distance in same distance unit

设某纵向距离单元的观测信号为

(11)

式中：M为该纵向距离单元内包含的散射点的总个数；σi为第i点的散射强度，且

(12)

对该信号进行离散化，并做FrFT，采样频率为fs，离散化后总点数为N。如果幅度最大时的角度为α0，离散化后回波信号的调频率估计值将由式(10)变为

(13)

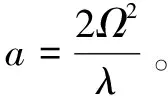
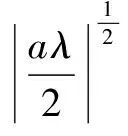
(14)

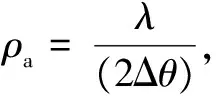
对基于FrFT的横向定标进行总结，其算法流程如图4所示。

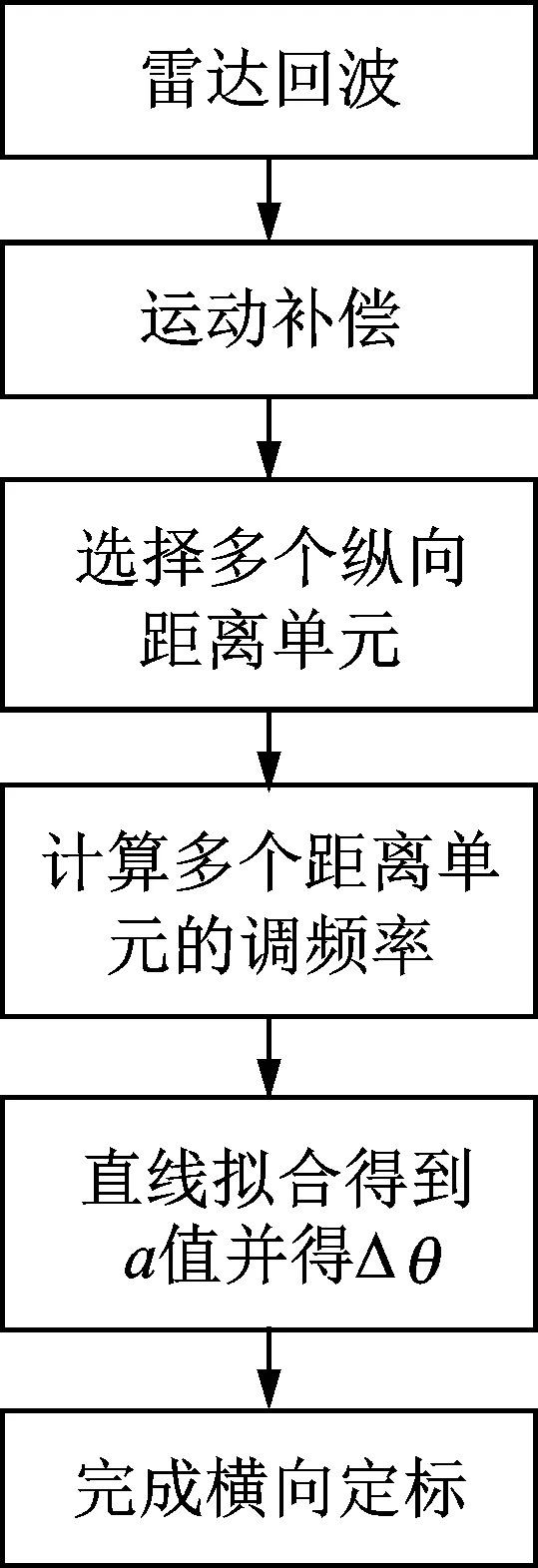
图4 基于FrFT的横向定标算法流程

Fig.4 Cross-range scaling flow based on FrFT

4 仿真实验

雷达发射线性调频信号，系统参数为：载频fc=10 GHz；信号带宽B=400 MHz；脉宽Tp=80 μs；脉冲重复频率PRF=250 Hz；采样频率fs=800 MHz；距离分辨率为0.375 m。仿真目标散射点模型如图5所示，目标尺寸为24 m×56 m，反射系数均为单位值。设定目标转台成像旋转角速度ω=0.03 rad/s。

图6为模拟目标未定标的ISAR图像，图像大小为246×278。由图6可见，图像未做定标，距离维和方位维像素代表的真实尺寸不一致，模型ISAR图像发生了明显变形，需要进行ISAR图像定标，调整图像的横向尺寸后，使图像反映出目标的真实形状，以便估计目标的真实尺寸。

对第195个距离单元的信号进行FrFT，结果在参数(α,u)平面上的二维分布如图7所示，FrFT阶数的取值范围定为0≤α≤2，FrFT域是指参数FrFT变换后的参数u。按照阈值对其进行二维搜索，得到峰值点所对应的旋转角α=1.578 7 rad/s，利用式(13)得到调频率的估计值为K=1.765 8 Hz/s。

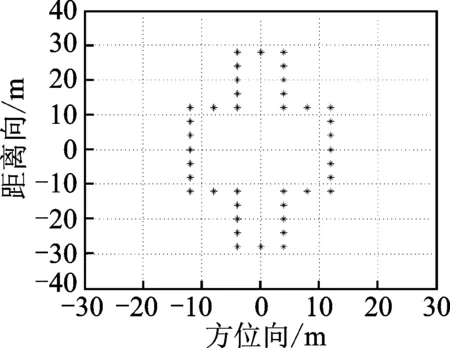
图5 模拟目标散射点模型

Fig.5 Scatter point model of simulated target

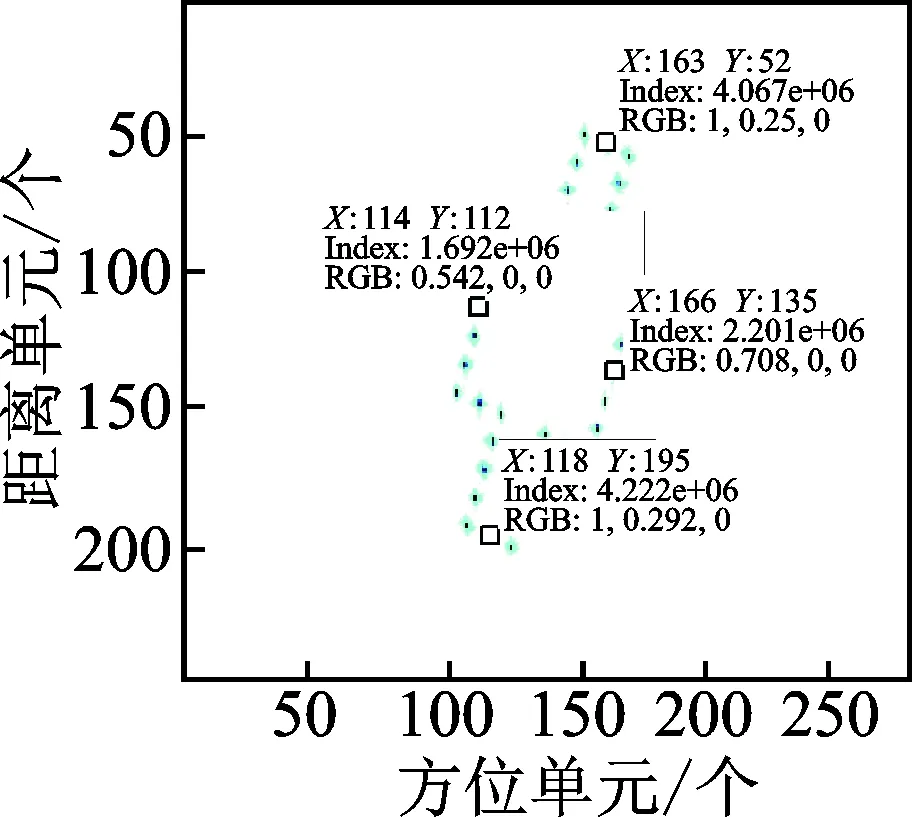
图6 模拟目标未定标ISAR图像

Fig.6 ISAR image without cross-range scaling

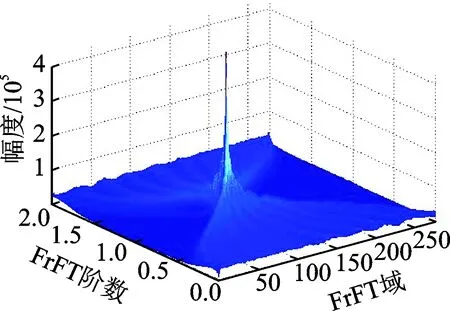
图7 第195个距离单元FrFT结果

Fig.7 FrFT of 195th distance unit

本文选取60个距离单元进行计算，先利用3σ准则剔除野值，再利用最小二乘准则进行拟合。图8为所选距离单元对应的纵向距离和调频率K值。利用最小二乘准则进行拟合，直线斜率的估计值为0.059 0 Hz/(m·s)-1，代入式(14)得到角速度的估计值为0.029 7 rad/s，横向分辨率为0.453 4 m。利用计算得到的目标横向分辨率，对目标横向尺寸进行调整，得到定标后的图像如图9所示。根据图6和图9可以计算出目标定标前后尺寸，如表1所示。

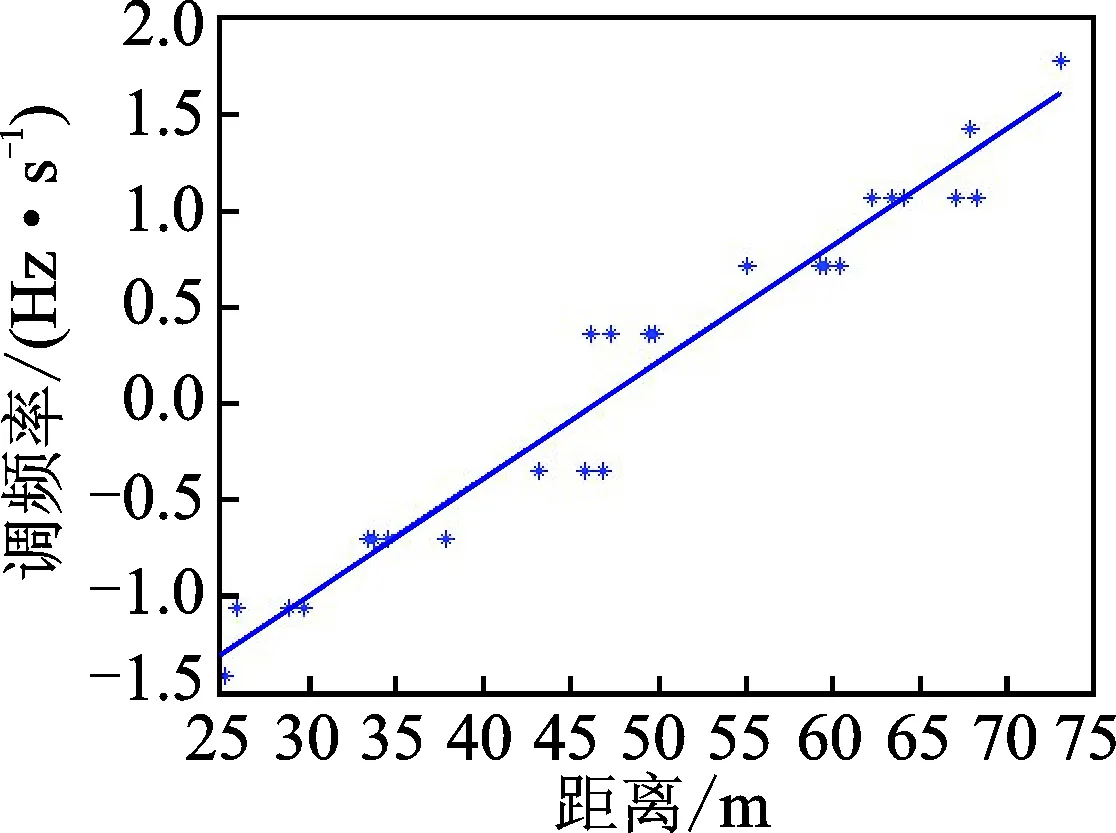
图8 多个距离单元估计结果

Fig.8 Multiple distance unit estim-ation results

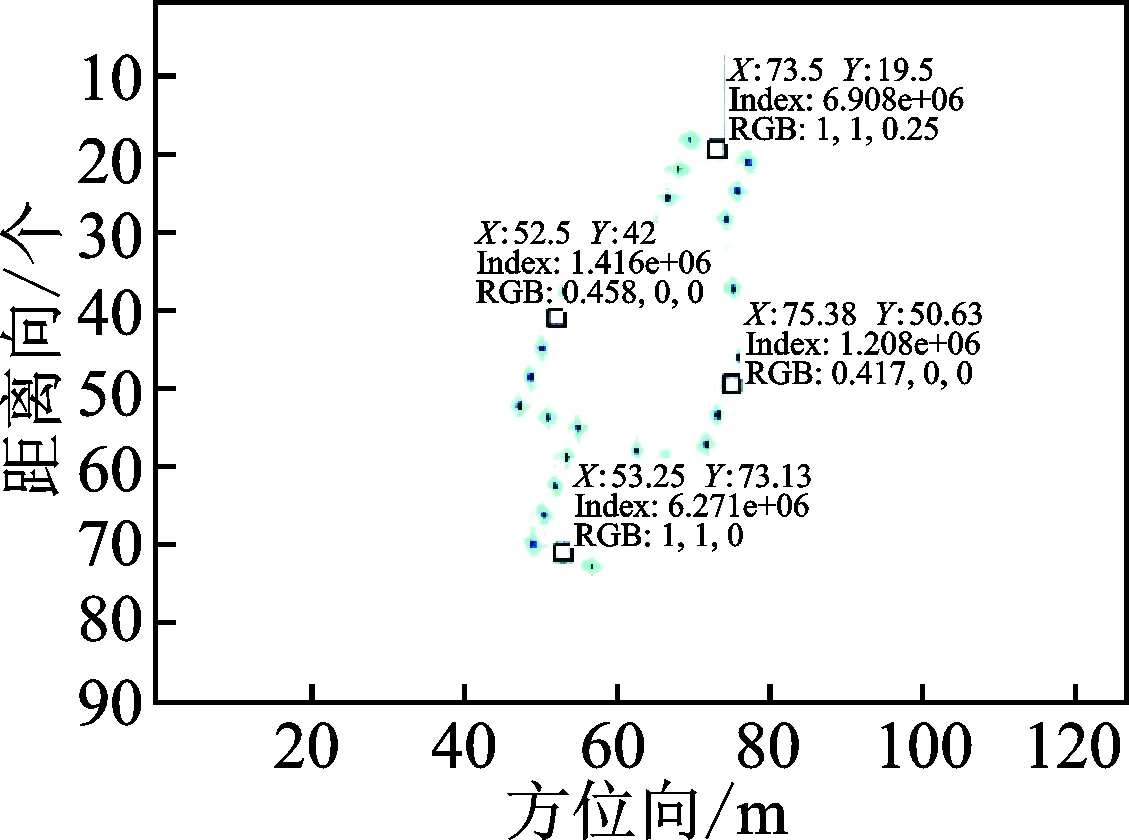
图9 定标后目标ISAR图像

Fig.9 ISAR image after cross-range scaling

表1 定标前后结果对比

定标前得到的目标尺寸为149.91×56.86，无法得到目标的真实尺寸，不利于后期的目标识别和特征提取。图8为定标后的结果，给出了模拟目标横向和纵向各两个点的位置，可以进一步计算得到目标横向长度24.45 m，纵向长度57.32 m，与模拟目标的仿真尺寸(24 m×56 m)比较接近。

5 结束语

转角估计是ISAR成像中方位向定标的前提，更是特征提取、目标识别等应用的基础。本文在慢时间域对回波信号进行了分析，确定了转动角速度和回波信号调频率之间的关系，并利用分数阶傅里叶变换估计目标回波信号的调频率，从而得到目标的有效转动角速度，进而完成横向定标。最后对卫星目标的运动进行了仿真成像，使用本文方法对仿真数据进行了处理，实验结果证明了本文方法的有效性和可行性。

[1] 保铮, 邢孟道, 王彤. 雷达成像技术 [M]. 北京: 电子工业出版社, 2005:230-231.

Bao Zheng, Xing Mengdao, Wang Tong. Radar imaging technology [M]. Beijing: Publishing House of Electronics Industry, 2005:230-231.

[2] 吕少霞. ISAR成像的横向定标算法研究 [D]. 哈尔滨: 哈尔滨工业大学, 2007: 6-12.

Lü Shaoxia. Cross-range scaling algorithm based on ISAR imaging[D]. Harbin: Harbin Institute of Technology, 2007: 6-12.

[3] Jiang Zhenglin, Bao Zheng. A new method of cross-range scaling of low resolution radar [J]. Journal of Electronics & Information Technology, 2001, 23(4): 365-372.

[4] 佘志舜, 朱兆达. 逆合成孔径雷达横向距离定标 [J]. 电子学报,1997, 25(3): 45-48.

She Zhishun, Zhu Zhaoda. Cross-range scaling of inverse synthetic aperture radar[J]. Acta Electronica Sinica,1997, 25(3): 45-48.

[5] Yuh C M,Xu Jia, Peng Yingning, et al. Cross-range scaling for ISAR based on image rotation correlation[J].IEEE Geoscience and Remote Sensing Letters, 2009, 6(3): 597-601.

[6] Martorella M. Novel approach for ISAR image cross-range scaling[J].IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1):281-294.

[7] 汪玲. 逆合成孔径雷达成像关键技术研究 [D]. 南京: 南京航空航天大学，2006:61-70.

Wang Ling. Study on key technologies of inverse synthetic aperture radar imaging[D]. Nanjing: Nanjing University of Aeronautics and Astronautics，2006:61-70.

[8] 莫正军, 涂亚庆, 刘良兵, 等. 基于重叠分段和FrFT的VCO非线性度检测方法[J]. 数据采集与处理, 2012,27(1): 96-100.

Mo Zhengjun, Tu Yaqing, Liu Liangbing, et al. VCO nonlinearity detection method based on overlapped subsection and FrFT[J]. Journal of Data Acquisition and Processing, 2012,27(1): 96-100.

[9] 邵高平, 安建平. 基于FFT和FRFT的非平稳干扰估计和抑制[J]. 数据采集与处理, 2010，25(2)：160-164.

Shao Gaoping, An Jianping. Estimation and suppression of broadband non-stationary interference based on FFT and FRFT[J]. Journal of Data Acquisition and Processing, 2010，25(2)：160-164.

[10] Zhao Yanbo, Yu Hua, Wei Gang, et al. FRFT-based parameter estimation of time-varying wideband underwater acoustic multipath channels [C]∥International Conference on Underwater Networks and Systems.Arlington:ACM,2015,9:22-24.

[11] Hou Huiling, Pang Cunsuo, Guo Hualing, et al. Study on high-speed and multi-target detection algorithm based on STFT and FRFT combination[J]. Optic-International Journal for Light and Electron Optics, 2016,127(2):713-717.

[12] 郭斌. 分数阶Fourier变换的基本原理和应用 [D]. 成都:电子科技大学, 2006:5-7.

Guo Bin. Fundamental principle and application of fractional Fourier transform[D].Chengdu: University of Electronic Science and Technology of China, 2006:5-7.

[13] 陈艳丽, 郭良浩,宫在晓. 简明分数阶傅里叶变换及其对线性调频信号的检测和参数估计[J]. 声学学报, 2015, 40(6): 761-771.

Chen Yanli, Guo Lianghao, Gong Zaixiao, The concise fractional Fourier transform and its application in detection and parameter estimation of the linear frequency-modulated signal[J]. Acta Acustica, 2015, 40(6): 761-771.

[14] 章步云, 刘爱芳, 朱晓华, 等. 基于分数阶Fourier变换的多分量LFM信号检测与参数估计[J]. 数据采集与处理, 2003,18(4):408-411.

Zhang Buyun, Liu Aifang, Zhu Xiaohua, et al. Multicomponent LFM signal detection and parameter estimation based on fractional Fourier transform[J]. Journal of Data Acquisition and Processing, 2003,18(4):408-411.

[15] 陶然, 邓兵, 王越. 分数阶傅里叶变换及其应用[M]. 北京：清华大学出版社, 2009:98-103.

Tao Ran, Deng Bing, Wang Yue. Fractional Fourier transform and its application [M]. Beijing: Tsinghua University Press, 2009：98-103.