基于多路欠采样的多分量LFM信号参数估计*

董宁斐 刘光祖 束 锋 王建新

(南京理工大学电子工程与光电技术学院，南京，210094)

引 言

线性调频(Linear frequency modulated, LFM)信号目前广泛应用于雷达、声呐和通信系统中，是脉冲压缩雷达经常采用的信号之一。作为大时宽带宽积信号，LFM信号通常具有超宽带特性，对其进行Nyquist采样是当前模数转换器面临的巨大挑战。基于中国余数定理，文献[1]提出了一种基于欠采样的宽带LFM信号参数估计方法，首先利用FFT、谱峰检测和中国余数定理进行宽带LFM信号的调频斜率无模糊估计，然后，在根据估计出的调频斜率对两路采样数据进行解线调处理之后，再利用类似的方法进行信号的初始频率无模糊估计。随后，文献[2]对上述方法进行改进，提出了一种针对LFM实信号的三路欠采样系统和参数估计方法，根据单路欠采样信号估计出调频斜率后，对三路采样速率不同的欠采样信号进行解线调处理，然后运用余数定理估计信号的初始频率。对于多分量LFM信号，文献[3]中提出了一种利用广义稳健余数定理同时对多个LFM分量的调制斜率和初始频率进行估计的方法，不过该方法要求各分量的调频斜率之间有明显差距。然而，实际情况下，有些雷达回波信号可能是调频斜率相同的多分量LFM信号，例如逆合成孔径雷达对高速运动目标的回波[4,5]，而上述方法均不适用于该类型的LFM信号。

基于压缩感知(Compressed sensing, CS)理论[6,7]，有学者指出，利用信号在某个变换域的稀疏性，也可以根据低速随机采样值实现信号的参数估计。文献[8]提出可以设计过完备的匹配字典，通过从冗余字典中寻找最佳匹配原子来实现LFM信号的参数估计。文献[9]利用LFM信号在时频域的稀疏性，在对信号进行压缩采样后直接对其短时傅里叶变换进行重构，然后利用Radon变换对重构的时频平面进行二维搜索，估计出信号的调频斜率和初始频率。文献[10]利用LFM信号在最佳分数阶傅里叶变换(Fractional Fourier transform, FrFT)域的能量聚集性，提出构造FrFT匹配矩阵进行信号检测和参数估计。该方法利用CS重构算法重构出信号在各个阶次FrFT矩阵中对应的系数向量，通过二维搜索得到最佳变换阶次，从而估计出信号的调频斜率和起始频率。虽然基于CS的参数估计方法对于单分量和多分量LFM信号同样适用，但是该类方法均需要采用高复杂度的重构算法[11,12]，运算量大，不易实现。

本文提出了一种基于亚奈奎斯特采样的多分量LFM信号参数估计方法，可以对具有相同调频斜率的多个分量进行调频斜率和初始频率估计。采样过程由多个采样速率相同但采样起始点不同的模数转换器(Analog to digital converter, ADC)实现，直接对LFM信号进行欠采样。参数估计过程中，首先根据单路欠采样序列的乘积型模糊函数(Product ambiguity function, PAF)[13]来估计信号的调频斜率，然后根据估计出的调频斜率对各路采样序列进行解线调处理，解线调后的序列为多频正弦信号。结合文献[14]中矩保持问题(Moment-preserving problem, MPP)的求解方法和文献[15]从多路欠采样序列中重构原始频域稀疏信号的BigBand方法，可以根据解线调后的各路序列估计出原始LFM信号各分量的初始频率。

1 信号模型与采样框架

假定观测信号x(t),t∈[0,T)由多分量LFM信号与高斯白噪声组成，频谱在区间[0,fnyq)内，其时域模型为

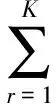
(1)

式中:K表示信号中的分量个数，Ar,κ,fr和φr分别表示各分量的幅度、调频斜率、初始频率和初始相位，v(t)表示高斯白噪声。本文对观测信号x(t)进行采样的过程如图1所示。

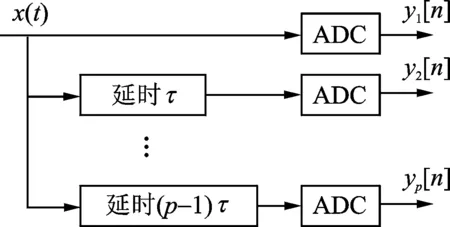
图1 多路欠采样过程Fig．1 Multiple-subsampling system

该采样系统由p个采样率为fs(fsp时，该系统总采样率低于观测信号x(t)的奈奎斯特采样率，实现了对信号的亚奈奎斯特采样。

在第i(1≤i≤p)个通道中，先将原始模拟信号延时(i-1)τ，然后直接对其以速率fs进行欠采样，得到序列yi[n]。由于序列yi[n]可理解为以速率1/τ对信号x(t)进行均匀采样所得样本的一部分，因此，若延时τ大于奈奎斯特采样间隔Tnyq=1/fnyq，则在频谱范围[1/τ,fnyq)内的信息丢失，可能会导致信号参数估计失败。由此可知，延时τ需满足τ≤1/fnyq。为简便起见，可设定τ=Tnyq，则对信号x(t),t∈[0,T)进行采样所得到的序列yi[n]可表示

(2)

式中Ts=1/fs，N=T/Ts，i′=i-1,0≤n≤N-1。

2 调频斜率估计

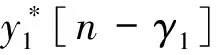
(3)

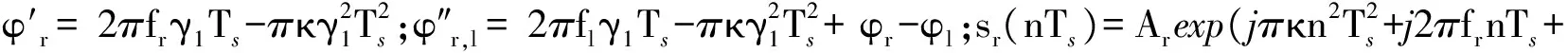
采样序列y1[n]在γ1Ts时刻的模糊函数(Ambiguityfunction,AF)切片定义为[16]

(4)

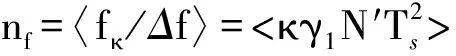
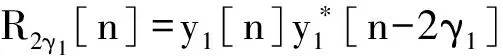
PAFy(γ,k)=AFy(γ1,k)·AFy(2γ1,2k) 0≤k≤N′/2-1

(5)

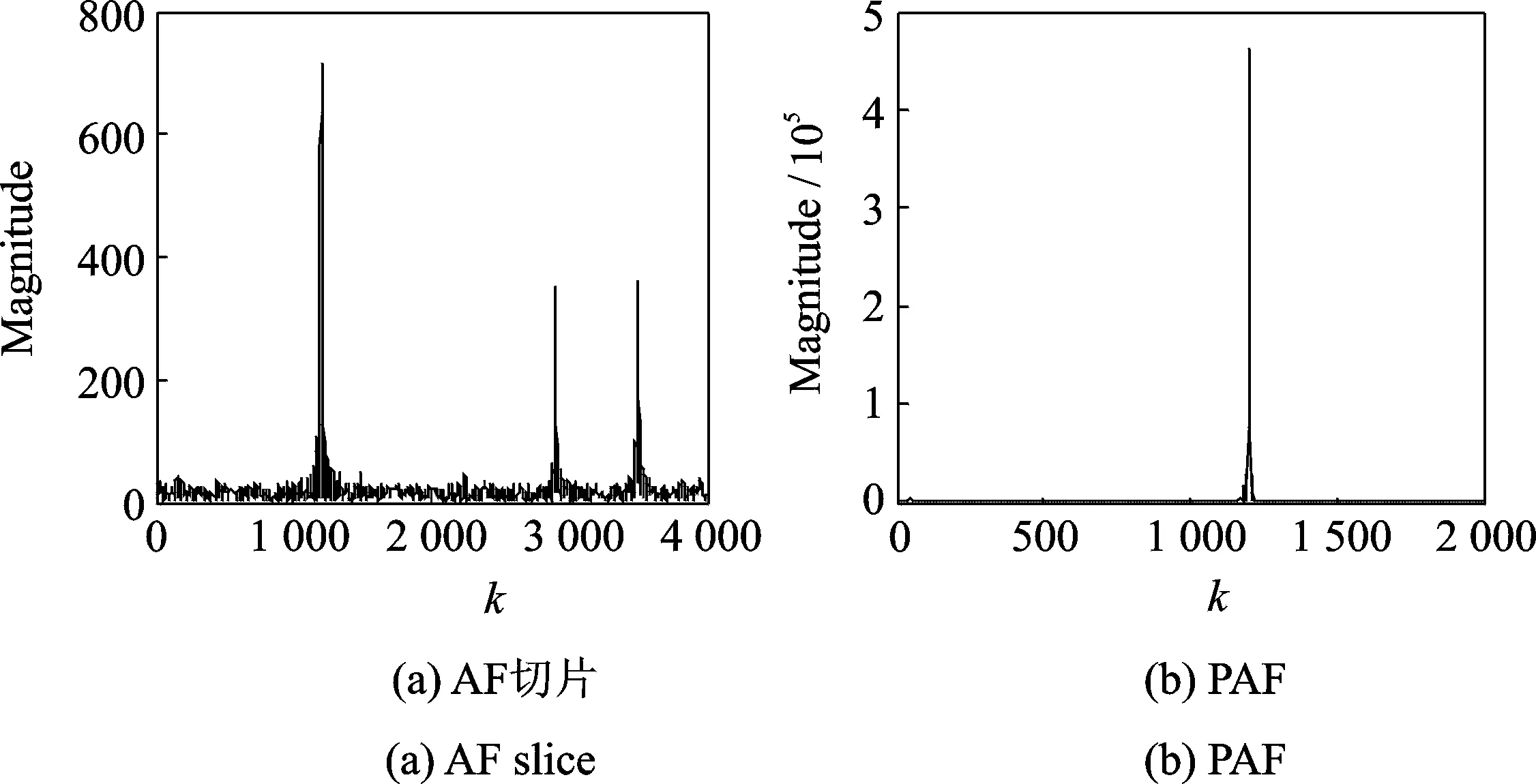
图2 两分量LFM信号的AF切片和乘积型模糊函数Fig．2 AF slice and PAF of a two-component LFM signal

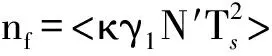
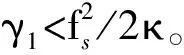
文献[17]中提到，当利用AF切片估计LFM信号的调频斜率时，均方根误差反比于γ1Ts(T-γ1Ts)3/2，γ1的最佳取值为γAF=<0.4T/Ts>。然而，本文利用的是欠采样序列的AF切片，需满足γ1≤T/2βTs，因此本文中γ1的最佳取值为γopt=。

3 初始频率估计

3.1 解线调处理

(6)

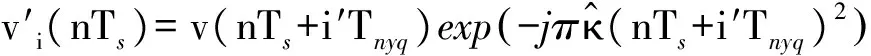
若是能够对LFM信号x(t),t∈[0,T)的奈奎斯特采样样本x[n]=x(nTnyq)进行解线调处理，则可以得到

(7)

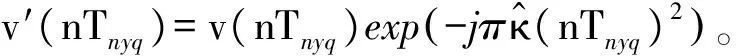
3.2 频域重构

(8)

式中i′=i-1。

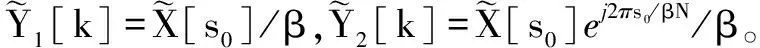
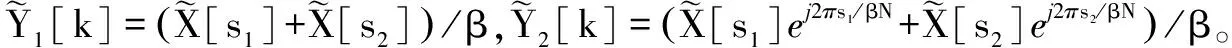
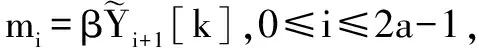
(9)

文献[14]指出，根据mi求解ql和zl的问题可以看作是MPP问题，并给出了a=2时的解析解如下

(10)

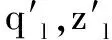
(11)

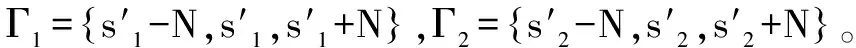
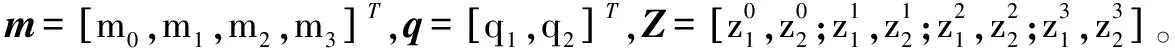
4 算法流程

本文根据欠采样序列yi[n](1≤i≤p，p=4)对多分量LFM信号x(t)进行参数估计的流程如下。

(1)分别求出采样序列y1[n]在γ1Ts时刻和2γ1Ts时刻的模糊函数切片并将其对应相乘，得到乘积型模糊函数PAFy(γ,k)，然后通过对PAFy(γ,k)进行峰值搜索实现对信号调频斜率的估计。

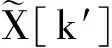
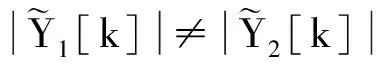
5 仿真实验

假设接收到的信号x(t)由K=3个幅度相同且调频斜率均为κ=6.01×1013Hz/s的LFM分量组成，信号持续时间为T=10 μs，频谱范围为[0,1) GHz，即fnyq=1 GHz。各LFM分量的初始相位在区间[0,2π)内随机选取,初始频率在区间[100,300 ]MHz内随机选取。仿真实验中采用由p=4个欠采样通道组成的采样系统对信号x(t)进行低速采样，每个通道的欠采样因子均为β，即采样过程的总采样率为ftot=pfnyq/β。另外，为了更好地测试算法本身的性能，避免分辨率Δf′对初始频率估计精度的影响，参数估计过程中设定R=32。

(12)

若eκ>0.001，则认为调频斜率估计失败。分别设定采样系统各通道的欠采样因子为β=4,β=8,β=16，其对应的估计成功率与信噪比之间的关系如图3所示。当调频斜率估计成功时，其对应的均方根误差(Root mean square error, RMSE)与信噪比之间的关系如图4所示，同时图4还给出了从奈奎斯特采样样本中估计调频斜率的克拉美罗界(Cramer-rao lower bound, CRLB)[18]。在本文提出的估计算法中，调频斜率是根据单路欠采样序列进行估计的，即估计过程所依据的样本个数为奈奎斯特采样样本数的1/β。因此，随着欠采样因子β的增大，调频斜率的估计性能有所降低。当SNR=-6 dB时，β=4对应的估计成功率在90%以上，均方根误差约为6×109Hz/s；而β=16对应的估计成功率仅有65%左右，均方根误差约为2.2×1010Hz/s。由图4可以看出，随着信噪比的增加，调频斜率估计的均方根误差有所降低，而β=16对应的均方根误差一直保持在β=4时的4倍左右。

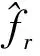
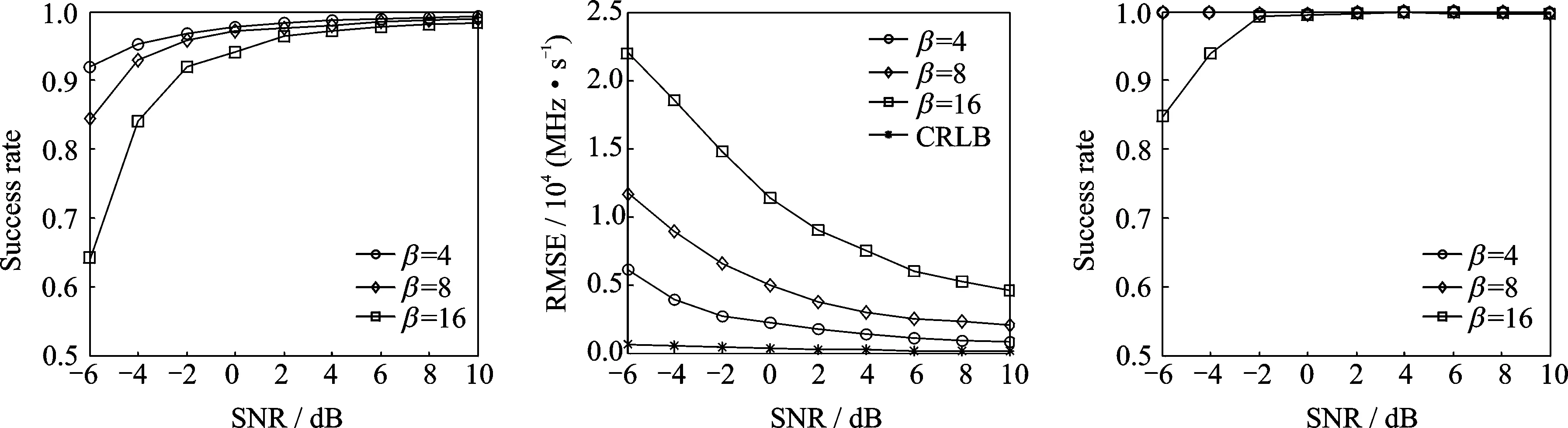
图3 调频斜率估计的成功率 图4 调频斜率估计的均方根误差 图5 初始频率估计的成功率 Fig．3 Success rate of chirp Fig.4 RMSE curves of chirp Fig.5 Success rate of initial rate estimation rate estimation frequency estimation

图6 3个LFM分量初始频率估计的均方根误差Fig．6 RMSE curves of initial frequency estimations of three LMF components

在本文提出的估计算法中，根据解线调处理之后的采样序列对信号的初始频率进行估计，因此初始频率的估计性能会受到调频斜率估计精度的制约，与奈奎斯特采样条件下的CRLB具有一定差距。当SNR=10 dB时，CRLB约为200 Hz，而本文算法在4≤β≤16条件下对应的均方根误差在4～30 kHz之间。

根据仿真结果可知，当β=4时，信噪比只需满足SNR≥-6 dB调频斜率的估计成功率即可达到90%以上，并且信号各分量的初始频率均能够根据调频斜率得以成功估计，估计的均方根误差在30 kHz以下。然而随着欠采样因子β的增加，即各通道采样率的降低，调频斜率估计和初始频率估计的性能均有所下降。因此，欠采样因子的选择需要折中考虑，在保证参数估计性能满足实际需求的情况下，尽可能地降低各通道的采样速率。

6 结束语

本文提出了一种基于多路欠采样的参数估计方法，可以对调频斜率相同、初始频率不同的多分量LFM信号进行参数估计。采样系统由多个采样起始点不同但采样速率相同的模数转换器组成，实现对LFM信号的亚奈奎斯特采样。信号的调频斜率根据欠采样序列的乘积型模糊函数进行估计。根据估计出的调频斜率对各路采样序列进行解线调处理后，利用矩保持问题的解析解和最小二乘法实现各分量初始频率的估计。该方法能够从亚奈奎斯特样本中估计出多分量LFM信号的调频斜率和初始频率，并且参数估计过程中运算简单，易于实现。

[1] 沈显祥, 叶瑞青, 唐斌, 等. 基于欠采样的宽带线性调频信号参数估计[J]. 电波科学学报, 2007, 22(1): 43-46.

Shen Xianxiang, Ye Ruiqing, Tang Bin, et al. An algorithm for estimation of wideband LFM signal parameters based on subsampling[J]. Chinese Journal of Radio Science, 2007, 22(1): 43-46.

[2] 余朋骏, 阮怀林. 宽带LFM 实信号多通道低速采样参数估计[J]. 电子信息对抗技术, 2014, 29(5): 25-31.

Yu Pengjun, Ruan Huailin. An algorithm for parameters estimation of wideband LFM real signal with multiple sub-sampling channels[J]. Electronic Information Warfare Technology, 2014, 29(5): 25-31.

[3] 梁红, 闫照南, 叶陈诚,等. 欠采样下多个线性调频信号参数估计方法[J]. 西北工业大学学报, 2014, 32(6): 888-893.

Liang Hong, Yan Zhaonan, Ye Chencheng, et al. An effective method for joint estimation of chirp rates and initial frequencies of multiple LFM signals with sub-Nyquist sampling[J]. Journal of Northwestern Polytechnical University, 2014, 32(6): 888-893.

[4] 杜小勇, 胡卫东, 郁文贤. 单自由度多分量线性调频信号的参数估计[J]. 信号处理, 2005, 21(5): 443-446.

Du Xiaoyong, Hu Weidong, Yu Wenxian. Parameter estimation of superimposed chirps with single degree of freedom[J]. Signal Processing, 2005, 21(5): 443-446.

[5] 阮航, 吴彦鸿, 叶伟. 匀速运动目标逆合成孔径激光雷达成像算法[J]. 红外与激光工程, 2014, 43(4): 1124-1129.

Ruan Hang, Wu Yanhong, Ye Wei. Inverse synthetic aperture ladar imaging algorithm for uniform motion targets[J]. Infrared and Laser Engineering, 2014, 43(4): 1124-1129.

[6] Donoho D. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[7] 宋耀良, 穆童. 从广义采样、小波到压缩感知[J]. 数据采集与处理, 2016, 31(4): 665-674.

Song Yaoliang, Mu Tong. From generalized sampling and wavelet to compressed sensing[J]. Journal of Data Acquisition and Processing, 2016, 31(4): 665-674.

[8] Joneidi M, Zaeemzadeh A, Rezaeifar S, et al. LFM signal detection and estimation based on sparse representation[C] // Annual Conference on Information Sciences and Systems. Baltimore: IEEE, 2015: 1-5.

[9] Zha S, Liu P, Huang J. Parameter estimation of LFM signal via compressive sensing [C] // International Radar Conference. Xi′an: IET, 2013: 1-5.

[10] 闫浩, 董春曦, 赵国庆. 基于压缩感知的线性调频信号参数估计[J]. 电波科学学报, 2015, 30(3): 449-456

Yan Hao, Dong Chunxi, Zhao Guoqing. Parameter estimation of LFM signal based on compressed sensing[J]. Chinese Journal of Radio Science, 2015, 30(3): 449-456.

[11] 王超. 基于压缩感知的贪婪迭代重构算法[J]. 数据采集与处理, 2012, 27(S2): 298-303.

Wang Chao. Greedy iterative reconstruction algorithm based on compressive sensing[J]. Journal of Data Acquisition and Processing, 2012, 27(S2): 298-303.

[12] Rabah H, Amira A, Mohanty B K, et al. FPGA implementation of orthogonal matching pursuit for compressive sensing reconstruction [J]. IEEE Transactions on Very Large Scale Integration Systems, 2015, 23(10): 2209-2220.

[13] Barbarossa S, Scaglione A, Giannakis G B. Product high-order ambiguity function for multicomponent polynomial-phase signal modeling [J]. IEEE Transactions on Signal Processing, 1998, 46(3): 691-708.

[14] Hsieh S H, Lu C S, Pei S C. Sparse fast Fourier transform by downsampling [C] // International Conference on Acoustics, Speech and Signal Processing. Vancouver: IEEE, 2013: 5637-5641.

[15] Hassanieh H, Shi L, Abari O, et al. GHz-wide sensing and decoding using the sparse Fourier transform [C] // Conference on Computer Communications. Toronto: IEEE, 2014: 2256-2264.

[16] Peleg S, Porat B. Linear FM signal parameter estimation from discrete time observations[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(4): 607-616.

[17] 朱延万, 赵拥军, 贾伍刚. 基于模糊函数切片和FrFT的快速LFM信号参数估计[J]. 信息工程大学学报, 2012, 13(2): 218-223.

Zhu Yanwan, Zhao Yongjun, Jia Wugang. Fast parameter estimation method for LFM signal based on ambiguity function slice and FrFT[J]. Journal of Information Engineering University, 2012, 13(2): 218-223.

[18] Peleg S, Porat B. The Cramer-Rao lower bound for signals with constant amplitude and polynomial phase[J]. IEEE Transactions on Signal Processing, 1991, 39(3): 749-752.